3.3. Линии первого порядка

Уравнение прямой с угловым коэффициентом.

Пусть дана некоторая прямая. Назовем углом наклона данной прямой к оси Ох угол α, на который нужно повернуть ось Ох, чтобы ее положи­тельное направление совпало с одним из направлений прямой. Угол α может иметь различные значения, которые отличаются друг от друга на величину ± п, где п  натуральное число. Чаще всего в качестве угла наклона берут наименьшее неотрицательное значение угла α, на который нужно повернуть (против часовой стрелки) ось Ох, чтобы ее положительное направление совпало с одним из направлений прямой (рис. 15). В таком случае < .

Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом этой прямой и обозначается буквой k: k = tg .

Если  = 0, т.е. прямая параллельна оси Ох, то k = 0. Если  = /2, т.е. прямая перпендикулярна оси Ох, то k = tg  теряет смысл. В таком случае говорят, что угловой коэффициент «обращается в бесконеч­ность».

Если известны угловой коэффициент k данной прямой и величина b отрезка 0В, который она отсекает на оси Оу (рис. 15) (т.е. данная прямая не перпендикулярна оси Ох), то уравнение рассматриваемой прямой имеет вид

y = kx + b . (1)

Уравнение (1) называют уравнением прямой с угловым коэффициентом. Если k = 0, то прямая параллельна оси Ох, и ее уравнение имеет вид у = b. Итак, уравнение любой прямой, не перпендикулярной оси Ох, имеет вид (1). Верно и обратное: любое уравнение вида (1) определяет прямую, которая имеет угловой коэффициент k и отсекает на оси Оу отрезок величины b.

Пример. Построить прямую, заданную уравнением у = .

Р е ш е н и е. Отложим на оси Оу отрезок OВ, величина которого равна 2 (рис. 16); проведем через точку В параллельно оси Ох отрезок, величина которого BN=4, и через точку N параллельно оси Оу отрезок, величина которого NM=3. Затем проведем прямую ВМ, которая и является искомой. Она имеет угловой коэффициент k=3/4 и отсекает на оси Оу отрезок величины b=2.

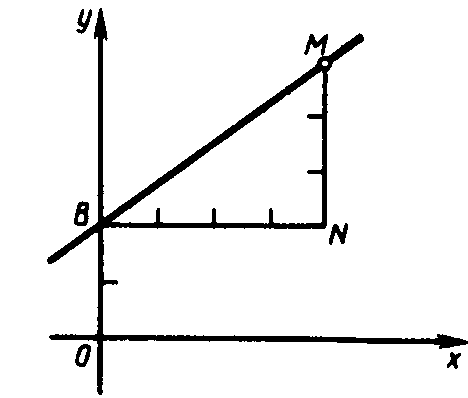
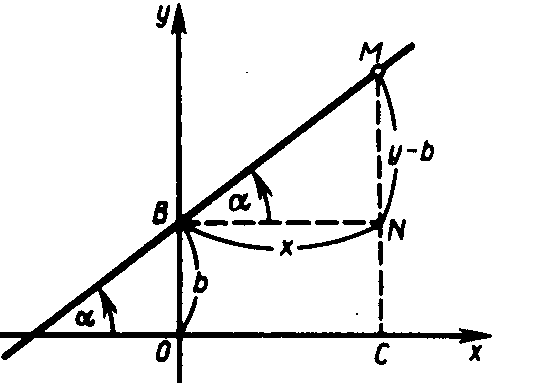
Рис.15 Рис. 16

2. Уравнение прямой, проходящей через данную точку, с данным угловым коэффициентом. В ряде случаев возникает необхо­димость составить уравнение прямой, зная одну ее точку M₁(х₁;у₁) и угловой коэффициент k. Запишем уравнение прямой в виде (1), где b  пока неизвестное число. Так как прямая проходит через точку М₁(х₁;y₁), то координаты этой точки удовлетворяют уравнению (1): y₁ = kх₁+b. Определяя b из этого равенства и подставляя в уравнение (1), получаем искомое уравнение прямой:

. (2)

З а м е ч а н и е. Если прямая проходит через точку M₁(x₁;y₁) перпендикулярно оси Ох, т. е. ее угловой коэффициент обраща­ется в бесконечность, то уравнение прямой имеет вид х  х₁ = 0. Формально это уравнение можно получить из (2), если разделить уравнение (2) на k и затем устремить k к бесконечности.

3. Уравнение прямой, проходящей через две данные точки. Пусть даны две точки М₁(х₁;y₁) и М₂(х₂;у₂) (рис. 17). Запишем уравнение прямой М₁М₂ в виде (2), где k  пока неизвестный угловой коэффициент. Так как прямая М₁М₂ проходит через точку М₂, то координаты этой точки удовлетворяют уравнению (2): у₂ – у₁ = k (x₂ — x₁). Определяя k из этого равенства (при условии ) и подставляя в уравнение (2), получаем искомое урав­нение прямой: .

Это уравнение, если , можно записать в виде

. (3)

Если у₁ = у₂ , то уравнение искомой прямой имеет вид у = у₁. В этом случае прямая параллельна оси Ох. Если х₁ = х₂ , то прямая, проходящая через точки М₁ и М₂ , параллельна оси Оу, и ее уравнение имеет вид х = х₁ .

Пример. Составить уравнение прямой, проходящей через точки М₁(3; 1) и М₂ (5; 4).

Р е ш е н и е. Подставляя координаты точек М₁ и М₂ в соот­ношение (3), получаем искомое уравнение прямой:

, или .

Рис. 17

4. Угол между двумя прямыми. Рассмотрим две прямые L₁ и L₂. Пусть уравнение прямой L₁ имеет вид , где , а уравнение прямой L₂  вид , где (рис. 18). Пусть φ  угол между прямыми L₁ и L₂ : 0  φ < π.

Из геометрических соображений устанавливаем зависимость между углами ₁ , ₂ , φ : ₂= ₁ + φ или φ = ₂ – ₁ . Поэтому

, или

(4)

Ф

ормула (4) определяет один из углов между прямыми. Второй угол равен π – φ.

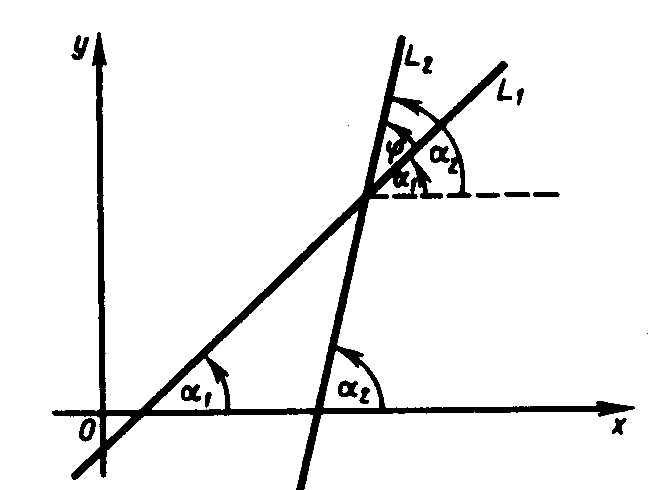
Рис 18

Пример. Две прямые заданы уравнениями у=2х+3 и у= 3х+2. Найти угол между этими прямыми.

Р е ш е н и е. Очевидно, k₁ = 2, k₂ = 3, поэтому по формуле (4) находим

Таким образом, один из углов между данными прямыми равен /4, другой угол   /4 = 3/4.

5. Условия параллельности и перпендикулярности двух прямых. Если прямые L₁ и L₂ параллельны, то φ = 0 и tg φ = 0. В этом случае числитель в правой части формулы (4) равен нулю: k₂  k₁ = 0, откуда k₂ = k₁. Таким образом, условием параллельности двух прямых является равенство их угловых коэффициентов.

Если прямые L₁ и L₂ перпендикулярны, т.е.  = /2, то , т. е. .

Таким образом, условие перпендикулярности двух прямых состоит в том, что их угловые коэффициенты обратны по величине и про­тивоположны по знаку. Это условие можно формально получить из формулы (4), если приравнять нулю знаменатель в правой части (4), что соответствует обращению tg φ в бесконечность, т. е. равенству .