2.4 Операции над множествами.
Множества можно определять также при помощи операций над некоторыми другими множествами.
Пусть имеются два множества: А и В.
1.
Объединением (суммой) множеств
А
и В
называется множество С,
состоящее из всех элементов множества
А
и всех элементов В
(в том числе и тех, которые принадлежат
А
и В).
Символически эту операцию можно записать
так: А
В={х
А
х
В},
здесь
-«или».
С=А+В=А В, например А={1,2,3}; В={2,3,4}.
С= А В={1,2,3,4}.
Если
А
В,
то А
В=В.
Для наглядности операций используют изображения множеств диаграммами или кругами Эйлера-Венна (рис.1).
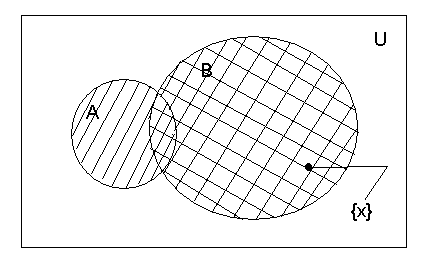
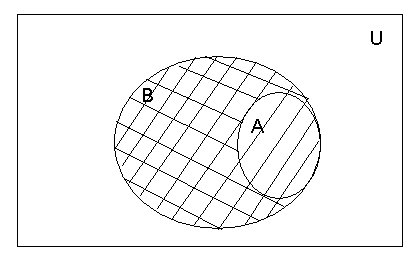
Рис.1.- Иллюстрация операции объединения кругами Эйлера
Аналогично
определяется объединение произвольной
(в том числе бесконечной) системы
множеств. Если система
содержит небольшое количество множеств,
то их объединение описывается явно
и т. д. В общем случае используется запись
,
которая читается так «Объединение всех
множеств
принадлежащих системе
».
Если же множества системы занумерованы
индексами, то используются следующие
варианты обозначений
-
для случая
,
-
для случая, когда совокупность индексов
множеств задана множеством I.
2.
Пересечением
множеств А
и В
называется множество С,
состоящее из элементов, входящих
одновременно в А
и В.
,
здесь
- операция «И»
если
,то
.
Например,
,
,
На случай нескольких множеств:
или
.
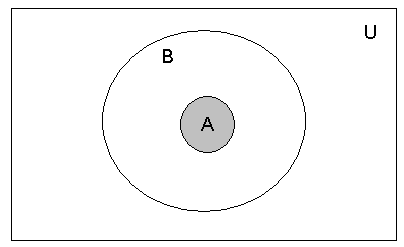
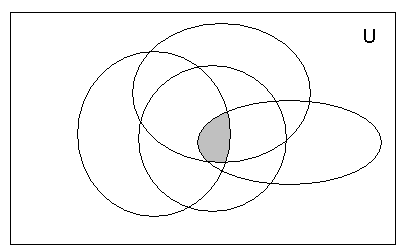
Рис.2 – Иллюстрация операции пересечения
Если
Ǿ.,
то такие множества называются
непересекающимися.
Система
множеств
,
в которой все непарные пересечения
пусты, называется разбиением множества
,
а множества такой системы называются
классами разбиений (рис.3).
;
;
;
;
;
-
разбиение множества
на классы
.
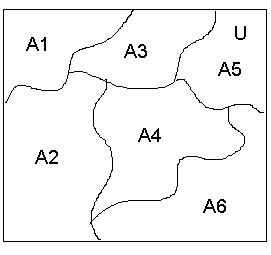
Рис.3-Разбиените множества на классы
Разностью множеств А и В называется множество С, содержащее элементы множества А и не содержащее элементы множества В.
(рис.4),например:
; ;
;
.
Если
,
то
.
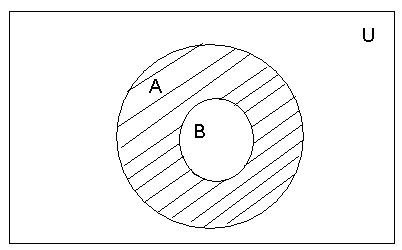
Рис.4.- Иллюстрация операции вычитания множеств
4. Симметрической разностью (дизъюнктивной суммой) называется множество С, элементы которого принадлежат либо А, либо В, но не обоим вместе (рис.5).
=
.
Например,
;
;
.
Рис.5.- Иллюстрация операции «симметрическая разность»
5. Абсолютным дополнением множества А до универсального множества называется множество, все элементы которого принадлежат и не принадлежат А (рис.6).
.
(рис.6). Очевидно, что
.
Дополнение
А определяется
отрицанием свойства
,
с помощью которого определяется
А.
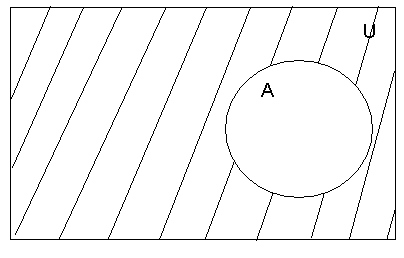
Рис.6.- Иллюстрация операции дополнение
Операции над множествами обладают некоторыми свойствами, как и операции над числами, т.е. подчиняются следующим законам:
1. Коммутативный закон (переместительное свойство)
;
.
;
2. Ассоциативный закон (сочетательное свойство).
;
;
;
3. Дистрибутивный закон (распределительное свойство)
;
;
4. Оригинальные операции:
5. Закон поглощения:
6. Теорема де Моргана:
,
7.
;
;
8.
;
3.Выводы. Рассмотренные положения теории множеств являются базовыми при изучении основных понятий и определений теории вероятностей и математической статистики. Для закрепления изученного материала необходимо ответить на контрольные вопросы и выполнить практические задания.
Контрольные вопросы
1.Указать в предложенных вариантах графическую интерпретацию дизъюнктивной суммы двух множеств:
а)
;
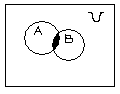б)
;
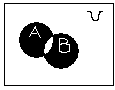в)
;
г)
.
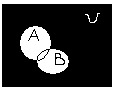2. Два множества А и В равны, если:
а) количество элементов в каждом из множеств равно (А+В)/2;
б) количество элементов в двух множествах одинаково;
в) они содержат одни и те же элементы;
г) количество элементов в сумме равно универсальному множеству.
3. Укажите операцию, которая не выполнима над множествами:
а) пересечение;
б) вычитание;
в) деление;
г) объединение;
д) симметрическая разность множеств;
е) абсолютное дополнение множества А до U.
4.
Какой из законов операций над множествами
описывает выражение
:
а) коммутативный;
б) дистрибутивный;
в) закон поглощения;
г) закон Деморгана;
д) ассоциативный.
5.Какие из приведенных соотношений неверны и почему?
а) хє{2, а, х}; б) 3є{1, {2, 3}, 4}; в) xє{1, sin(x)}; г) {x, y}є{а,{х, в}.
Практическое занятие №1
Задача 1.Приняв множество первых 20-ти натуральных чисел в качестве универсального, запишите следующие его подмножества:
А – четных чисел; В – нечетных чисел; С – квадратов чисел; D – простых нечетных чисел.
В каких отношениях находятся эти подмножества?
Решение:
U={1, 2, 3, 4,…, 20};
A={2, 4, 6, 8, 10, 12, 14, 16, 18, 20};
B={1, 3, 5, 7, 9, 11, 13, 15, 17, 19};
C={1, 4, 9, 16};
D=1, 3, 5, 7, 11, 13, 17, 19};
A
B=U;
D
B.
Задача 2. Запишите множества, получаемые в результате следующих операций над множествами из предыдущей задачи:
A
B,
A∩B, A∩C, A∩D, C\A, C\B, C+
.
Сформулировать определяющие свойства каждого из полученных множеств.
Решение:
A B=U; A∩B=Ø; A∩C={4, 16} – квадраты четных чисел; A∩D=Ø; C\A={1, 9} – квадраты нечетных чисел; C\B={4, 16}=A∩C;
C+ ={1, 4, 9, 16}∆{2, 4, 6, 8, 9, 10, 12, 14, 16, 18, 20}=
=(C\ ) ( \C)={1}∪{2, 6, 8, 10, 12, 14, 16, 18, 20}.
Задача 3.
Три прибора x, y, z сравнивают по 2-м показателям, причем выделяют тот из приборов, у которого данный показатель наилучший (случаи одинаковых показателей исключаются).
а) образуйте мн-во U всевозможных исходов такого сравнения, обозначив элементы этого мн-ва парами букв. Для приборов с наилучшими показателями (например исход ух означает, что по первому показателю лучшим оказался прибор у, а по второму – прибор х).
б) перечислите элементы множеств возможных исходов, при которых:
(А) – прибор х оказался лучшим по первому показателю;
(В) – прибор х оказался лучшим по второму показателю;
(С) – прибор х оказался лучшим хотя бы по одному показателю;
(D) – прибор х оказался лучшим по обоим показателям;
(Е) – прибор х не является лучшим ни по одному из показателей.
Задача 4.
В химическом продукте могут оказаться примеси четырех видов, обозначенных через a, b, c, d. Приняв в качестве исходного множества А={a, b, c, d}, образуйте множество всех его подмножеств Р(А). Дайте содержательное истолкование этого множества и его элементов. Каким ситуациям соответствует, в частности, несобственные подмножества.
Задача 5.
Дайте словесное описание каждому из следующих множеств:
а) {х׀ х – точка плоскости, находящаяся на расстоянии 2 от начала координат};
б)
{х׀
-4х+3=0};
в) {х׀ х – инженер нашего отдела};
г) {хєR׀ х=3к, кєN};
е) {2х+1׀ х – целое число}.
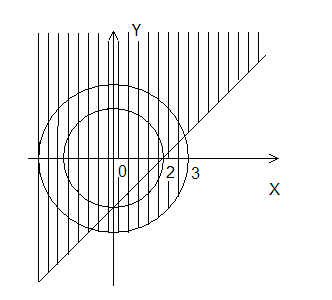
Задача 6. Изобразить на рисунке множества A B, A∩B, A\B, B\A, A∆B, если:
A={(x,y)є
;
4≤,𝑥-2.+,𝑦-2.≤9};
B={(x,y)є
;
y
A
B
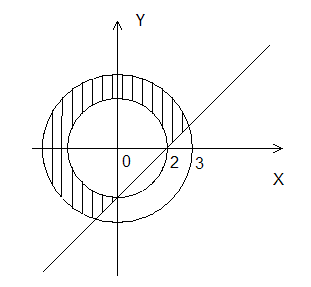A∩B
A\B
B\A
A∆B=(A\B)
(B\A)
Задача 7 Доказать тождества:
1 A\(A\B)=B\(B\A);
2. (A\B)\C=(A\C)\(B\C);
3. A∩(B C)=A∩B A∩C
4) A (B\A)=A∪B;
5) A∩(B\A)=Ø;
6) A\(A∩B)=A\B;
7)A∩(B\C)=(A∩B)\C;8)A\(B∩C)=(A\B) (A\
32. Какой из нижеперечисленных способов является способом задания множества с помощью порождающей пары:
а) А = { 1, 2, 3, 4, …};
б) А = { 3, 5, 7, 11, …};
в) А = { 1, 2, 4, 8, 16, …};
г) А = { 2, 32, 8, 16, …}.
33. Что обозначает символ “U” в основных операциях над множествами:
а) дизъюнктивная сумма;
б) пересечение множеств;
в) абсолютное дополнение;
г) объединение множеств.