
- •Лекция № 3 Введение. Классификация событий. Действия над событиями
- •2. События. Классификация событий. Пространство элементарных событий
- •4. Практические занятия
- •Лекция№5:Условная вероятность. Формула полной вероятности и формула Байеса. Независимые случайные события
- •1.1 Распределение Релея
- •1 Система двух случайных величин
- •1.Введение
- •4. Практические занятия
- •2.Элементы теории множеств.
- •2.1 Определение множества. Мощность множества. Подмножества.
- •2.2 Множества и подмножества.
- •2.3 Способы задания множеств. Универсальное множество.
- •2.4 Операции над множествами.
- •Практическое занятие №2
- •Тема: Основные понятия комбинаторики.
- •2. Перестановки, размещения.
- •3. Сочетания.
- •4. Разбиение на группы:
- •1. Введение
- •3. Алгебра событий
- •1. Введение
- •2. События. Классификация событий. Пространство элементарных событий
- •Примеры.
- •3. Алгебра событий
- •События Вi образуют полную группу событий, если
- •Особый интерес представляют полные группы несовместимых событий
- •План лекции:
- •2. Классический способ задания вероятностей.
- •3. Статистическая вероятность
- •4. Геометрическая вероятность.
- •Лекция№5
- •2. Формула полной вероятности.
- •3. Формула Байеса (теорема гипотез).
- •4. Независимые случайные события.
- •Контрольные вопросы и тесты
- •2 Закон распределения случайной величины.
- •3. Функция распределения
- •4. Плотность распределения случайной величины
- •Практическое занятие №1
- •1.Математическое ожидание , мода и медиана случайной величины
- •2. Моменты. Дисперсия. Среднее квадратическое отклонение.
- •3. Моменты высших порядков
- •Математическое ожидание, мода и медиана случайной величины
- •2. Моменты. Дисперсия. Среднее квадратическое отклонение.
- •3. Моменты высших порядков
- •Практическое занятие №1
- •5. Контрольные вопросы и задания
- •1. Биномиальное распределение
- •2. Распределение Пуассона
- •3. Простейший поток событий
- •1. Испытания (схема) Бернулли. Биномиальное распределение
- •Если ставить вопрос о появлении события а k-раз в n испытаниях в произвольном порядке, то событие представимо в виде
- •2. Распределение Пуассона.
- •3. Простейший поток событий
- •Задача 4
- •Задача 5
- •Задача 6
- •Практическое занятие № 2
- •5. Контрольные вопросы
- •1.1 Равномерное распределение вероятностей
- •1.2 Показательное (экспоненциальное) распределение
- •1.3 Нормальное распределение
- •Задача 1
- •Решение
- •Решение
- •Задача 4
- •Задача 6
- •Практическое занятие №2
- •2. Рекомендуемые фрагменты программ
- •1.1 Распределение Релея
- •1.1 Распределение Релея
- •1.2 Распределение Максвелла
- •1.3 Логарифмическое нормальное распределение
- •2. Функция случайной величины.
- •Практическое занятие №1
- •3. Рекомендации к выполнению.
- •Практическое занятие №2
- •Задача3
- •1 Система двух случайных величин
- •1 Система двух случайных величин
- •1.2 Плотность распределения двух случайных величин
- •1.3 Условные функция распределения и плотность распределения
- •1.4 Корреляция двух случайных величин
- •Аналогично имеем
- •2. Система произвольного числа случайных величин
- •Задача1
- •Практическое занятие №2 Тема: Исследование системы двух случайных величин
- •Так как под интегралом в (1) находится неотрицательная величина, то, выбросив из интервала интегрирования отрезок ав, мы значение интеграла не увеличим, т.Е.
- •2. Характеристические функции
- •Для дискретной случайной величины х с законом распределения
- •Свойства характеристической функции
- •3. Центральная предельная теорема
- •2. Числовые характеристики выборки
- •2.1. Выборочное среднее
- •Выборочная дисперсия
- •3. Статистический ряд. Статистическая функция распределения
- •4. Статистическая совокупность. Гистограмма
- •1. Оценка параметров
- •2. Метод наибольшего правдоподобия для нахождения оценок
- •3. Метод наименьших квадратов
1 Система двух случайных величин
1.1 Функция распределения двух случайных величин
1.2 Плотность распределения двух случайных величин
1.3 Условные функция распределения и плотность распределения
вероятностей
1.4 Корреляция двух случайных величин
2. Система произвольного числа случайных величин
1 Система двух случайных величин
1.1 Функция распределения двух случайных величин
До сих пор рассматривались ситуации, в которых фигурировала одна случайная величина. Однако, при изучении случайных явлений приходится пользоваться двумя, тремя и более случайными величинами. Так при анализе радиотехнической системы иногда нужно найти связь между входными и выходными сигналами для одного или двух моментов времени.
Координаты
точки разрыва снаряда в пространстве
при стрельбе по воздушной цели определяется
тремя случайными величинами , а сама
точка может рассматриваться как случайная
точка пространства. Систему из n
случайных величин
![]() можно рассматривать как случайную точку
в n-мерном
пространстве . Чтобы научиться
анализировать такие системы , необходимо
расширить понятия функции распределения
и плотности распределения вероятностей
. Сначала рассмотрим систему двух
непрерывных случайных величин.
можно рассматривать как случайную точку
в n-мерном
пространстве . Чтобы научиться
анализировать такие системы , необходимо
расширить понятия функции распределения
и плотности распределения вероятностей
. Сначала рассмотрим систему двух
непрерывных случайных величин.
Пусть имеется две непрерывные случайные величины X и Y.
Определение.
Двумерная функция распределения
вероятностей случайных величин X
и Y
– это вероятность события
![]() ,
то есть
,
то есть
![]() ,
где (X<x,Y<y)=
{ X<x
}{Y<y
} –означает произведения событий.
,
где (X<x,Y<y)=
{ X<x
}{Y<y
} –означает произведения событий.
Пользуясь геометрической интерпретацией системы (X,Y), как случайной точки на плоскости, можно дать геометрическое истолкование функции распространения F(x,y); это есть вероятность попадания случайной точки (X,Y) в бесконечный квадрат, лежащие левее и ниже ее.
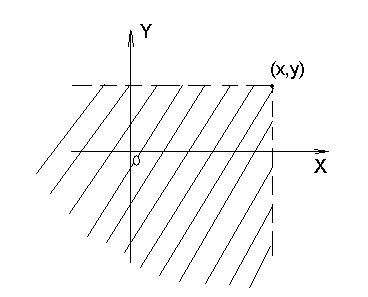
Легко
вывести следующие свойства функции
![]() :
:
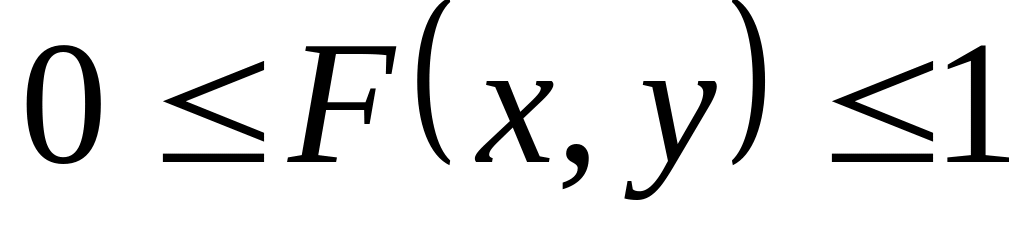 ;
; ;
;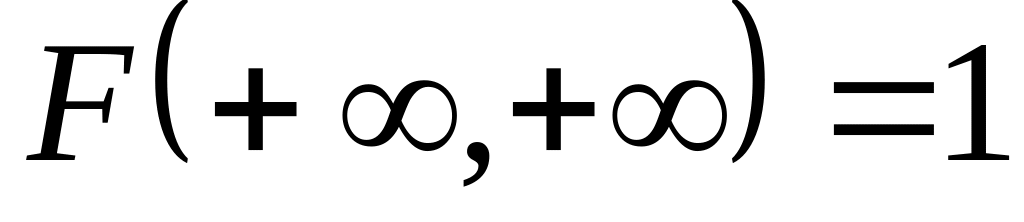 ;
;- неубывающая функция по одной их переменных;
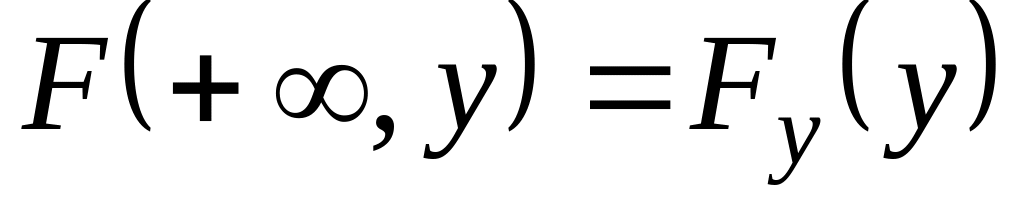 ,
,
 - функции распределения случайных
величин X
и Y.
- функции распределения случайных
величин X
и Y.
Зная
функцию распределения F(х,y)
можно найти вероятность попадания с.
т. (X,Y)
в пределы прямоугольника R
,ограниченного абсциссами (![]() )
и ординатами (
)
и ординатами (![]() ).
P{(X,Y)
R}=F(
).
P{(X,Y)
R}=F(![]() )-F(
)-F(![]() )-F(
)-F(![]() )+F(
)+F(![]() ).
(Здесь вероятность попадания в квадрат
с вершиной в т. (
)
вычли дважды, поэтому ее нужно прибавить)
).
(Здесь вероятность попадания в квадрат
с вершиной в т. (
)
вычли дважды, поэтому ее нужно прибавить)

1.2 Плотность распределения двух случайных величин
Плотность распределения случайных величин (X ,Y) определяется соотношением
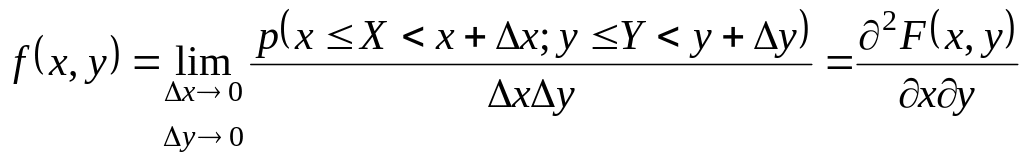 ,
,
если предел существует.
Свойства плотности распределения вероятностей:
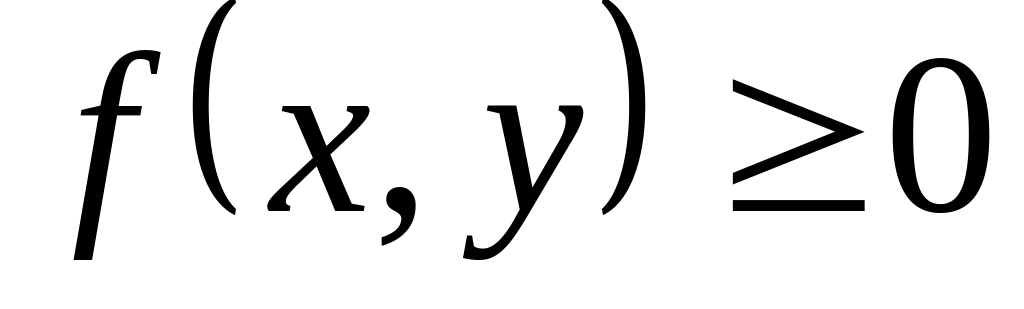 ,
,
 ;
;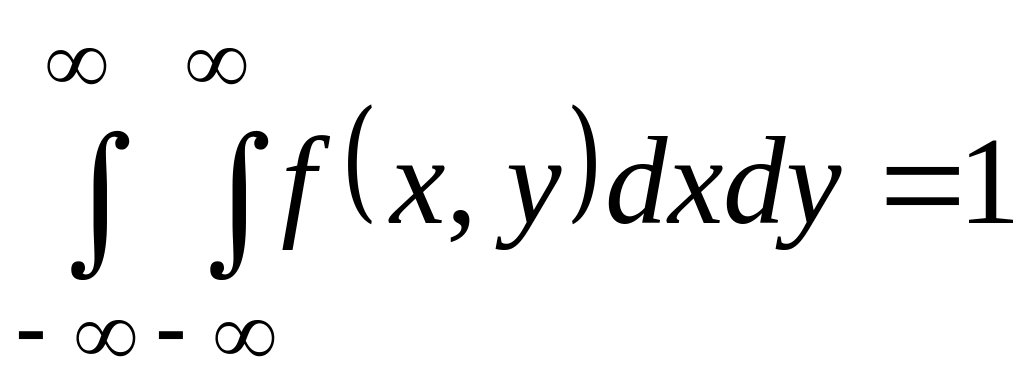 ;
;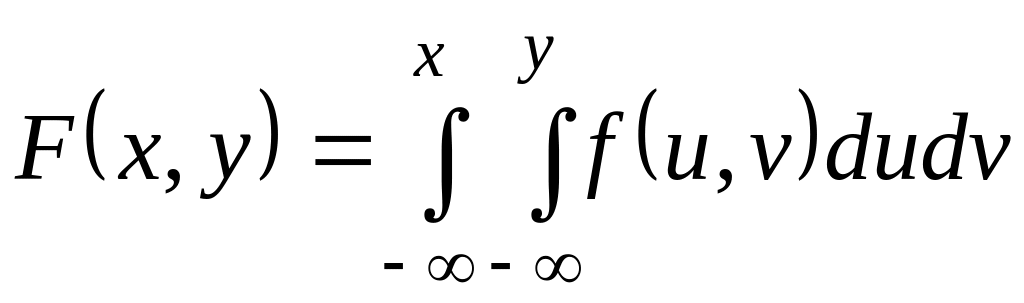 ;
; ,
,
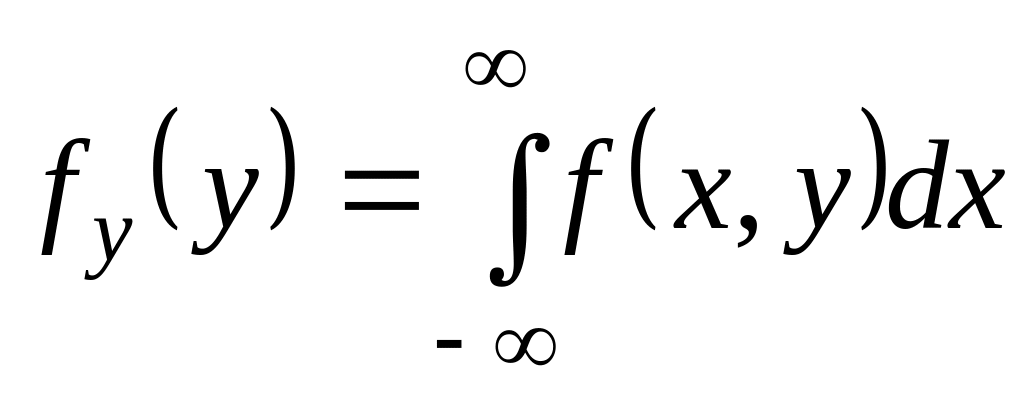 ,
где
,
где
 и
и
 - плотности распределения случайных
величин X
и Y;
- плотности распределения случайных
величин X
и Y;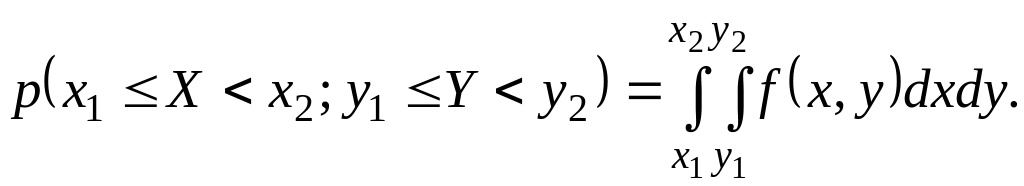
Графически плотность распределения вероятностей можно представить как некоторую поверхность над плоскостью X0Y.
В ведение
плотности вероятностей двух случайных
величин позволяет определить математическое
ожидание функции двух случайных величин
g(X,Y):
ведение
плотности вероятностей двух случайных
величин позволяет определить математическое
ожидание функции двух случайных величин
g(X,Y):
![]()
В частности , если g(X,Y)=XY, то
![]() .
.
1.3 Условные функция распределения и плотность распределения
вероятностей
Подобно случайным событиям случайные величины подразделяются на зависимые и независимые, но определение здесь имеет несколько иной характер. Из здравого смысла ясно, что отклонение индуктивности колебательного контура (одна случайная величина) и емкости (другая случайная величина) от номинального значения вследствие дефектов в их производстве – есть независимые случайные величины. Также независимы напряжения помех, проникающих от двух или нескольких независимых (разных) источников.
Две случайные величины называются зависимы, если закон распределения вероятностей одной из них меняется в зависимости от того, какое значение приняла другая.
Степень зависимости может быть разной. Одна может быть жесткой – например, шумовое напряжение на сопротивлении R принимает значение u, то ток равен
![]() .
.
В других случаях зависимость между случайными величинами является менее определимой . Между двумя крайними случаями – функциональной зависимости и полной независимости двух случайных величин – существует бесконечное множество промежуточных ситуаций , при которых зависимость так или иначе проявляется. Для зависимых случайных величин вводят понятие условных законов распределения.
По аналогии с функцией распределения вероятностей вводится и условная функция распределения. Функцией распределения вероятностей случайной величины Х при условии, что событие М произошло, называется вероятность того, что случайная величина Х примет значение меньше чем, х при условии, что событие М произошло:
![]() .
.
Если р(М)>0, то условную функцию распределения можно представить, как вероятность того, что совместно случайная величина Х приняла значение меньше х и произошло событие М, деленную на вероятность появления события М, т.е.
![]() .
.
Условная функция распределения вероятностей обладает всеми свойствами функции распределения:
 ;
;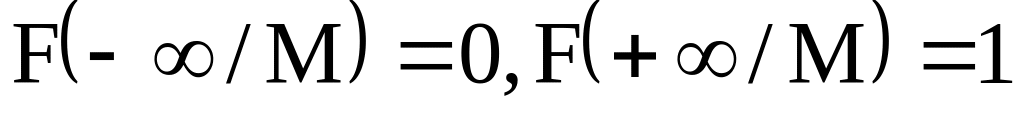 ;
;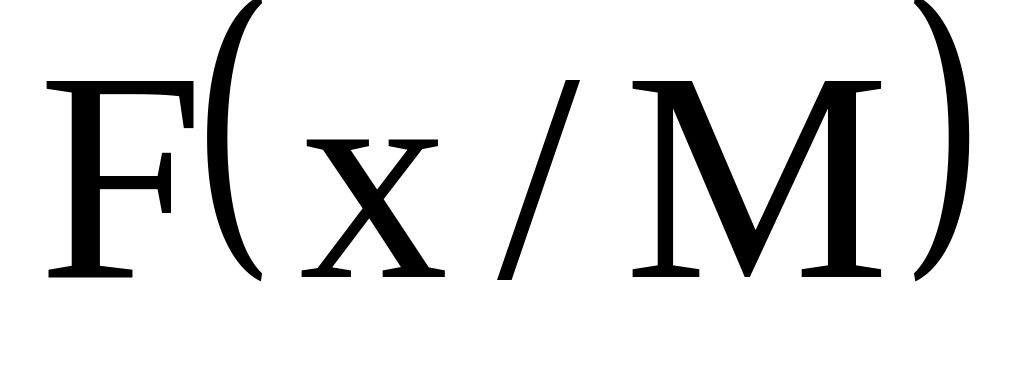 -
неубывающая функция;
-
неубывающая функция;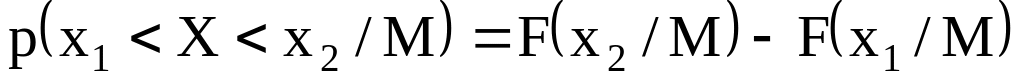 ,
,
если
![]() .
.
В качестве примера построения условной функции распределения рассмотрим ситуацию, когда событие М состоит в том, что случайная величина Х примет значение меньше некоторого числа m. Пусть x<m. Запишем
![]() .
.
Так
как событие
![]() содержит событие, состоящее в том, что
Х примет значение меньше х
содержит событие, состоящее в том, что
Х примет значение меньше х
![]() ,
то
,
то
![]() .
Поэтому для
.
Поэтому для
![]()
![]() .
Если
.
Если
![]() ,
то событие
,
то событие
![]() содержит событие
,
а значит
содержит событие
,
а значит
![]() .
.
Итак
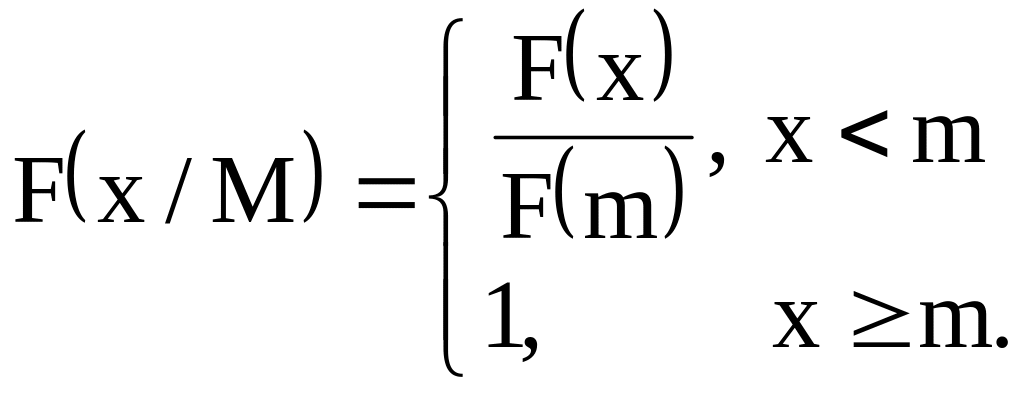 .
.
Условная плотность вероятностей определяется как
![]()
при условии существования производной и обладает всеми свойствами плотности вероятностей.
Пусть
у нас имеется случайная величина X
и событие А, состоящее в том, что случайная
величина Y<y,
т.е.
![]() .
Ясно , что
.
Ясно , что
![]() .
Тогда согласно определению условной
функции распределения случайной величины
X
при условии, что Y<y
имеем
.
Тогда согласно определению условной
функции распределения случайной величины
X
при условии, что Y<y
имеем
![]() .
.
Аналогично получаем
![]()
Если
через событие А обозначить
![]() ,
то тогда
,
то тогда
 если
предел существует.
если
предел существует.
Условная плотность вероятностей случайной величины X при условии, что случайная величина Y=y по определению равна
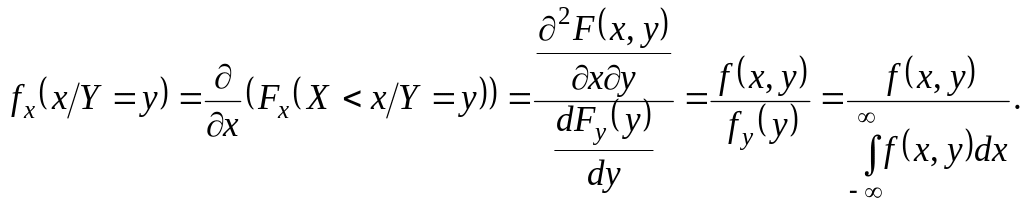
Аналогично

Индексы х, у в вышеприведенных формулах часто опускают и условные плотности вероятностей обозначают
![]()
![]() .
.
Из формул
![]() ,
,
![]()
можно получить вариант формулы Байеса для непрерывных случайных величин:
![]() .
.
