1.4 Корреляция двух случайных величин

Определение. Случайные величины X и Y независимы, если

.

Пример. Случайные тепловые падения напряжения на двух резисторах электрической схемы.

1. Следствие. Для независимых случайных величин X и Y

то есть математическое ожидание произведения случайных величин равно произведению математических ожиданий.

2. Следствие. Для независимых случайных величин Х и Y условная плотность вероятностей

-

равна безусловной плотности вероятностей.

Аналогично имеем

.

Если случайные величины X иY не независимы, то вводится понятие корреляции двух случайных величин.

Определение. Корреляцией или корреляционным моментом двух случайных величин X и Y называется математическое ожидание произведения центрированных случайных величин

Если обозначить , , а их значения соответственно , , то

С другой стороны , так как и , то

Определение. Нормированный корреляционный момент называется коэффициентом корреляции:

Для дискретных случайных величин интеграл заменяется суммой, т.е.

Рассмотрим два случая . В первом случае пусть X,Y – независимые случайные величины , тогда и

Таким образом, если случайные величины X и Y независимы , то их корреляционный момент (и коэффициент корреляции) равен нулю.

Рассмотрим другой случай, когда случайные величины жестко связаны линейной зависимостью

.

Если случайная величина Х принимает значение х, то функция - определяется законом распределения случайной величины Х, а значит

Поэтому

.

Легко показать, что отсюда и

,

Можно показать, , что всегда .

Н иже приведены графики зависимости дискретных случайных величин для различных коэффициентов корреляции.

О тметим, что коэффициент корреляции говорит о линейной зависимости случайных величин. Можно показать, например, что при нелинейной связи у=kx², где случайная величина Х имеет симметричный закон распределения относительно нуля коэффициент корреляции также равен нулю.

Коэффициент корреляции можно представить в виде

.

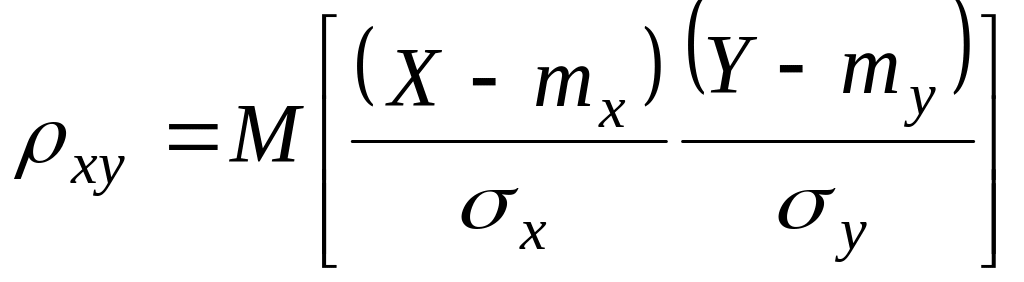Если выполнить интегрирование, то получаем, что

является безразмерной величиной.

Пример. Пусть случайные величины X и Y (входные и выходные величины системы) связаны линейной связью:

,

где n – независимая шумовая величина с M[n]=0 (здесь учитывается и нелинейные эффекты). Найдем дисперсию Y, т.е. - мощность выхода системы. Так как

,

то

Обозначим мощность которую вносит в у величина х , через и , которую вносит n - . Имеем

, .

Найдем коэффициент корреляции между X и Y :

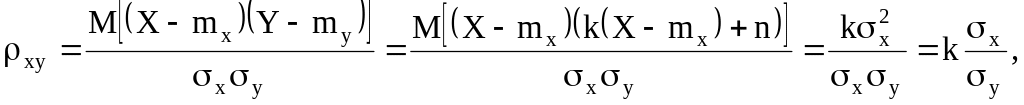
отсюда и

Это соотношение называется соотношением для линейно обусловленной выходной мощности.

2. Система произвольного числа случайных величин

Пусть имеется n (n>2) случайных величин (Х₁, Х₂, ..., Х_n). Функция распределения системы вводится как обобщение функции распределения двух случайных величин

F(x₁, x₂, ..., x_n) = p(X₁<x₁, X₂<x₂, ... , X_n<x_n)

Эта функция обладает всеми свойствами, какими обладает функция распределения двух случайных величин. Она неубывающая функция одной переменной при фиксированных остальных. Кроме того

F(- , x₂, ..., x_n)=...= F(x₁, x₂, ..., -)=F(- , -, ..., x_n)=F(- , -, ...,- )=0;

F₁(x₁)=F(x₁, , ..., ) – функция распределения случайной величины х₁;

F₂(x₁, х₂)=F(x₁, х₂, ,..., ) – функция распределения системы (Х_1, Х₂) и т.д.;

F(, , ..., ) = 1.

Аналогично системе двух случайных величин вводится плотность распределения вероятностей:

если соответствующая производная существует.

Плотность распределения системы (X₁, X₂, ..., X_m) (m < n) равна

По плотности распределения f(x₁, x₂, ..., x_n) находится функция распределения

Отсюда

Условная плотность распределения определяется по формуле

Если случайные величины Х₁, Х₂, ..., Х_n независимы, то плотность распределения системы (Х₁, Х₂, ..., Х_n) равна

f(x₁, x₂, ..., x_n) = f₁(x₁) f₂(x₂) ... f_n(x_n).

Практическое занятие №1