4. Независимые случайные события.

Определение независимых событий в теории вероятностей играет большую роль. Введем понятие независимости двух событий. Естественно считать, что событие А не зависит от события В, если его вероятность не зависит от того, произошло ли событие В или нет, т.е. Р(А/В) = Р(А)

С учетом этого обстоятельства дается определение независимости двух событий.

Определение: Случайные события А и В, А , В , называются независимыми, если Р(АВ) = Р(А)Р(В).

События А и В попарно независимы, из независимости А вытекает В.

Если имеется несколько событий, то их попарная независимость еще не означает их зависимость в совокупности.

В основе независимости событий лежит их физическая независимость, сводящаяся к тому, что множества случайных факторов, приводящих к тому или иному исходу опыта, не пересекаются, или почти не пересекаются.

На практике события считаются независимыми, исходя из физических соображений, если не находят механизма, при помощи которого осуществлялась бы связь между ними.

Три события считаются независимыми, если они попарно независимы и выполняется условие:

.

В общем случае, когда имеется n событий , они считаются независимыми, если

для индексов, пробегающих набор целых чисел меньших или равных n.

Пример: Два раза бросается монета.

Тогда ={ГГ,ГР,РГ,РР};

А – первый раз выпал герб,

В – второй раз выпал герб.

А={ГГ,ГР}; АВ={ГГ}; Р(АВ)=1/4;

В={ГГ,РГ}; Р(А)=2/4; Р(В)=2/4=1/2;

Р(АВ)=Р(А) Р(В)=1/21/2=1/4;

Следовательно, А и В независимые события.

Практическое занятие №1

Контрольные вопросы и тесты

1. Определить вероятность случайного события. Сформулировать основные аксиомы и законы теории вероятностей.

2. Обосновать многообразие методов определения вероятности случайного события, дать рекомендации по их применению.

3.. Обосновать необходимость использования вероятностных моделей и методов в практике инженеров телекоммуникаций.

4. Случайные события А и В (АCΩ, ВCΩ) называются независимыми, если выполняются следующие условия:

а) Р(А*В)=Р(В)*Р(А);

б) Р(А*В)=Р(А)+Р(В);

в) Р(А*В)=Р(А/В)+Р(А)+Р(В);

г) Р(А*В)=Р(А)*Р(В/А).

5. Под событием понимают :

а) всякий факт, который в результате реализации комплекса условий обязательно произойдет;

б) явление, которое при определенном эксперименте возможно произойдет;

в) всякий факт, который в результате опыта может произойти или не произойти;

г) явление, которое при любом опыте обязательно произойдет.

6. Два события А и В являются равносильными если:

а) они принадлежат одному и тому же множеству;

б) они определяются одним и тем же множеством;

в) являются подмножествами одного и того же множества;

г) при каждом испытании появление события В влечет появление события А.

7. Формула Байеса применяется когда:

а) когда априорная вероятность известны и равны Р(Н) и производится опыт, в результате опыта появляется событие А и необходимо найти апостериорную вероятность гипотез;

б) вероятность до опыта неизвестны, но известны апостериорные вероятности и гипотезы, высказанные относительно результата. Необходимо найти априорные вероятности;

в) вероятности до опыта известные и равны Р(Н) = 1. Предполагается, что в результате опыта появляется событие А; необходимо найти апостериорные вероятности;

г) априорные вероятности известны и в результате опыта появляется событие А, необходимо найти апостериорные вероятности гипотез.

8. Из урны, содержащей 4 белых и 3 черных шара вынимают ( одновременно или последовательно) два шара. Найти вероятность того, что оба шара будут белыми Р(С).

а) Р(С) = 4/7 ;

б) Р(С) = 2/7;

в) Р(С) = 1/2;

г) Р(С) = 3/7.

Задача 1. Система состоит из 7 элементов, надёжность каждого элемента 0,75. Для повышения надёжности предлагается резервирования по следующей схеме:

Определить надёжность системы.

Задача 2, Система состоит из 5 – ти элементов, надёжность каждого элемента равна 0,8. Для повышения надёжности предлагается резервирование всей системы в целом. На сколько % увеличится надёжность системы?

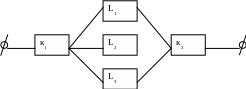
Задача 3. Между корреспондентами М и N происходит обмен информацией по схеме приведённой ниже , где к₁и к₂ - оконечная аппаратура, а L_1, L_2,L₃ - каналы взаимно резервирующие друг друга. Выходы из строя элементов схемы – независимые события. Вероятности безотказной работы элементов к₁и к₂ , L_1,L_2,L₃ за время Т соответственно равны 0,8; 0,7; 0,9; 0,6; 0,5. Какова вероятность того, что за время Т не произойдёт нарушения связи?

Практическое занятие №2

Задача 1. Прибор состоит из 2-х дублирующих друг друга узлов и может работать в одном из двух режимов: нормальном и неблагоприятном. Нормальный режим наблюдается в 80% случаев эксплуатации, неблагоприятный – в 20% случаев. Надежность (вероятность безотказной работы) каждого из узлов в нормальном режиме равно 0,9 в неблагоприятном – 0,6. При выходе из строя (отказе) узла происходит автоматическое и безотказное переключение на дублера. Найти полную вероятность Р(А) безотказной работы прибора.

Задача 2. Имеется 3 канала связи. Статистика такова, что по первому каналу передается 3 сообщения без искажения и 1 с искажением, по второму каналу 2 сообщения без ошибок и 3 сообщения с ошибками, по третьему каналу передается 3 сообщения без ошибок. Получатель информации наугад подключается к одному из каналов и принимает правильное безошибочное сообщение. Найти апостериорную вероятность того, что правильное сообщение было принято по первому каналу.

Задача 3. По каналу связи, подверженному воздействию помех, передается одна из двух команд управления в виде кодовых комбинаций 11111 и 00000, причем априорные вероятности передачи этих команд соответственно равны 0,7 и 0,3. Из-за наличия помех вероятность правильного приема каждого из символов (1 и 0) уменьшается до 0,6. Предполагается, что символы кодовых комбинаций искажаются независимо друг от друга. На выходе приемного устройства зарегистрирована комбинация 10110. Найти вероятность того, что передана команда 11111.

Задача 4. Сообщение может передаваться по одному из n каналов связи, находящихся в разных состояниях из них n₁ каналов в отличном состоянии, n₂ – в хорошем, n₃ – в посредственном, n₄ – в плохом (n₁ +n₂ + n₃ + n₄ = n). Вероятность правильной передачи сообщения для разного вида каналов равна, соответственно Р₁, Р₂, Р₃, Р₄. Для повышения достоверности сообщение передается два раза по одному и тому же каналу, который выбирается наугад. Найти вероятность того, что хотя бы один раз оно будет передано правильно _.

Задача 5. Детали, изготовляемые цехом, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадет к 1-му контролеру, равна 0,6, ко 2-му –0,4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна – 0,94; вторым – 0,98. Годная деталь была признана стандартной. Каким контролером вероятнее всего была проверена деталь?

Задача 6. Для участия в студенческих отборочных спортивных соревнованиях выделено из 1й группы курса 4 студента, из 2й –6, из 3й –5 студентов. Вероятность того, что студент 1й, 2й, и 3й группы попадет в сборную института, соответственно равны 0,9; 0,7; 0,8. Наугад выбранный студент в итоге соревнования попал в сборную. К какой из групп вероятнее всего принадлежал этот студент?

Задача 7 Прибор может работать в трех режимах: 1) нормальном; 2)форсированном; 3) недогруженном. Нормальный режим соблюдается в 70% работы прибора, форсированный в 20%, и недогруженный в 10%. Надежность прибора для нормального режима равна 0,85, для форсированного – 0,5, для недогруженного – 0,9. Определить надежность прибора.

Задача 8. До опыта об его условиях можно было сделать четыре гипотезы: Н₁, Н₂, Н₃, Н₄ с вероятностями, равными соответственно: Р(Н₁)=0,2; Р(Н₂)=0,1; Р(Н₃)=0,5; Р(Н₄)=0,2. В результате опыта появилось событие А, которое невозможно при гипотезах Н₁, Н₂ и достоверно при гипотезах Н₃, Н_4. Найти апостериорные вероятности гипотез.

Задача 9. В двух партиях однотипных изделий содержится соответственно а и в изделий, причем, в каждой партии одно изделие бракованное. Наугад взятое изделие из 1й партии перекладывается во вторую, после чего из 2й партии наугад выбирается одно изделие. Какова вероятность Р(А) того, что изделие окажется бракованным?

Задача 10. Вероятность того, что параметры одного из трех блоков радиостанции (антенного – фидерного устройства, приемника или передатчика) выйдут за время полета из допусков равны соответственно 0,1; 0,2; 0,3. В случае, если из поля допусков вышли параметры одного блока, связь не будет установлена с вероятностью 0,25; двух блоков – 0,4; трех блоков – 0,5. Найти вероятность Р(А) того, что связь не будет установлена.

Задача 11. По каналу связи передается два сигнала. Вероятность прихода первого сигнала вдвое больше вероятности прихода второго. Приемное устройство при воспроизводстве первого сигнала переводит его во второй с вероятностью 0,1; а второй в первый – с вероятностью 0,2. Определить вероятность получения первого сигнала.

Лекция №6

Тема:. Понятие случайной величины. Закон распределения случайной величины. Функция распределения. Плотность распределения.

Литература:

1. Математичні основи теорії телекомунікаційних систем . Під ред.Поповського В.В. - Харків, СМИТ, 2011.

2. Венцель Е.С. Овчаров Л.А. Теория вероятностей и ее инженерные приложения. -М.: Наука,1988.-480 с.

3. Гмурман В.Е. Теория вероятностей и математическая статистика.-М.:Высш.шк.,1999.-479 с..

План лекции:

1. Понятие случайной величины.

2 Закон распределения случайной величины.

3. Функция распределения случайной величины

4. Плотность распределения случайной величины

1. Понятие случайной величины.

Одним из основных понятий теории вероятностей является понятие случайной величины. Случайной величиной (с.в.) называется величина (число - вещественное или комплексное), которая в результате опыта может принять то, или иное значение (до проведения опыта неизвестное). С точки зрения инженерного подхода случайная величина - это просто числовое описание исходов случайного опыта. С точки зрения математики, случайная величина - это функция, которая определена на пространстве элементарных событий.

X = (),   ; x_i = (_i).

Примеры случайных величин:

1. Время между заявками в потоке заявок,

2. Время безотказной работы некоторого технического устройства,

3. Отношение сигнал/помеха на входе приемника

4. Число очков, выпадающих при однократном бросании игральной кости.

5. Величина затуханий в каналах связи.

Разнообразие случайных величин весьма велико. Число принимаемых ими значений может быть конечным, счетным и несчетным; значения случайной величины могут быть расположены дискретно или заполнять интервалы сплошь.

Случайные величины будем обозначать заглавными буквами латинского алфавита (X, Y, Z,...), а их значения прописными буквами ( х, у, z,...).

Различают два основных типа случайных величин: дискретные и непрерывные.

Дискретная случайная величина - это величина, множество возможных значений которой конечно или счетно.

Непрерывная случайная величина - это величина, множество возможных значений которой континуально.

В приложениях теории вероятностей, как правило, имеют дело не с самими случайными событиями, а со случайными величинами. Это связано с тем, что в результате проведения опыта обычно регистрируется значение случайной величины X(_i) = x_i а не регистрируется, каким элементарным исходом _i закончился сам опыт, т.е. регистрируется значение функции, а не ее аргумента.

Поясним это на примере бросании игральной кости, где случайная величина Х - число выпавших очков. Из механики известно, что движение твердого тела полностью определяется, если заданы в некоторый момент шесть параметров, определяющих положение тела в пространстве, вместе со скоростями изменения этих параметров. Под элементарным событием _i будем понимать набор этих двенадцати параметров в момент бросания. Тогда, зная _i мы знаем и x_i, т.e. X есть функция . Множество , возможных значений  конечно, так как двенадцать параметров могут колебаться в конечных интервалах, а мы регистрируем их лишь с конечным числом десятичных знаков. Очевидно, что Х() наблюдать легко, в то время как при регистрации _i возникают непреодолимые трудности. Кроме того, возможных значений _i очень много, а значений Х(_i) всего шесть. Отсюда видно, насколько сильно может быть упрощение математического описания явления при переходе от случайного события к случайной величине.