
- •Лекция № 3 Введение. Классификация событий. Действия над событиями
- •2. События. Классификация событий. Пространство элементарных событий
- •4. Практические занятия
- •Лекция№5:Условная вероятность. Формула полной вероятности и формула Байеса. Независимые случайные события
- •1.1 Распределение Релея
- •1 Система двух случайных величин
- •1.Введение
- •4. Практические занятия
- •2.Элементы теории множеств.
- •2.1 Определение множества. Мощность множества. Подмножества.
- •2.2 Множества и подмножества.
- •2.3 Способы задания множеств. Универсальное множество.
- •2.4 Операции над множествами.
- •Практическое занятие №2
- •Тема: Основные понятия комбинаторики.
- •2. Перестановки, размещения.
- •3. Сочетания.
- •4. Разбиение на группы:
- •1. Введение
- •3. Алгебра событий
- •1. Введение
- •2. События. Классификация событий. Пространство элементарных событий
- •Примеры.
- •3. Алгебра событий
- •События Вi образуют полную группу событий, если
- •Особый интерес представляют полные группы несовместимых событий
- •План лекции:
- •2. Классический способ задания вероятностей.
- •3. Статистическая вероятность
- •4. Геометрическая вероятность.
- •Лекция№5
- •2. Формула полной вероятности.
- •3. Формула Байеса (теорема гипотез).
- •4. Независимые случайные события.
- •Контрольные вопросы и тесты
- •2 Закон распределения случайной величины.
- •3. Функция распределения
- •4. Плотность распределения случайной величины
- •Практическое занятие №1
- •1.Математическое ожидание , мода и медиана случайной величины
- •2. Моменты. Дисперсия. Среднее квадратическое отклонение.
- •3. Моменты высших порядков
- •Математическое ожидание, мода и медиана случайной величины
- •2. Моменты. Дисперсия. Среднее квадратическое отклонение.
- •3. Моменты высших порядков
- •Практическое занятие №1
- •5. Контрольные вопросы и задания
- •1. Биномиальное распределение
- •2. Распределение Пуассона
- •3. Простейший поток событий
- •1. Испытания (схема) Бернулли. Биномиальное распределение
- •Если ставить вопрос о появлении события а k-раз в n испытаниях в произвольном порядке, то событие представимо в виде
- •2. Распределение Пуассона.
- •3. Простейший поток событий
- •Задача 4
- •Задача 5
- •Задача 6
- •Практическое занятие № 2
- •5. Контрольные вопросы
- •1.1 Равномерное распределение вероятностей
- •1.2 Показательное (экспоненциальное) распределение
- •1.3 Нормальное распределение
- •Задача 1
- •Решение
- •Решение
- •Задача 4
- •Задача 6
- •Практическое занятие №2
- •2. Рекомендуемые фрагменты программ
- •1.1 Распределение Релея
- •1.1 Распределение Релея
- •1.2 Распределение Максвелла
- •1.3 Логарифмическое нормальное распределение
- •2. Функция случайной величины.
- •Практическое занятие №1
- •3. Рекомендации к выполнению.
- •Практическое занятие №2
- •Задача3
- •1 Система двух случайных величин
- •1 Система двух случайных величин
- •1.2 Плотность распределения двух случайных величин
- •1.3 Условные функция распределения и плотность распределения
- •1.4 Корреляция двух случайных величин
- •Аналогично имеем
- •2. Система произвольного числа случайных величин
- •Задача1
- •Практическое занятие №2 Тема: Исследование системы двух случайных величин
- •Так как под интегралом в (1) находится неотрицательная величина, то, выбросив из интервала интегрирования отрезок ав, мы значение интеграла не увеличим, т.Е.
- •2. Характеристические функции
- •Для дискретной случайной величины х с законом распределения
- •Свойства характеристической функции
- •3. Центральная предельная теорема
- •2. Числовые характеристики выборки
- •2.1. Выборочное среднее
- •Выборочная дисперсия
- •3. Статистический ряд. Статистическая функция распределения
- •4. Статистическая совокупность. Гистограмма
- •1. Оценка параметров
- •2. Метод наибольшего правдоподобия для нахождения оценок
- •3. Метод наименьших квадратов
1.3 Логарифмическое нормальное распределение
В системах связи затухание сигнала при прохождении его по тракту выражается как
![]()
![]() ,
,
где
![]() и
и
![]() - мощности выходного и входного сигналов.
Из экспериментов известно, что затухание
А очень часто ведет себя как гауссовская
случайная величина. Отсюда возникает
задача определения плотности вероятностей
отношения мощностей. Для решения этой
задачи введем две случайные величины
X и Y ,
связанные соотношением X=eY
, считая, что Y
представляет собой гауссовскую случайную
величину с математическим ожиданием
- мощности выходного и входного сигналов.
Из экспериментов известно, что затухание
А очень часто ведет себя как гауссовская
случайная величина. Отсюда возникает
задача определения плотности вероятностей
отношения мощностей. Для решения этой
задачи введем две случайные величины
X и Y ,
связанные соотношением X=eY
, считая, что Y
представляет собой гауссовскую случайную
величину с математическим ожиданием
![]() и дисперсией
и дисперсией
![]() .
Можно показать , что плотность распределения
вероятностей для Х имеет вид
.
Можно показать , что плотность распределения
вероятностей для Х имеет вид

Это и есть логарифмически нормальная плотность распределения вероятностей.
Математическое ожидание и дисперсия соответственно равны
![]()
![]() .
.
2. Функция случайной величины.
При решении технических задач часто встречаются ситуации, когда одна случайная величина является функцией другой с известным законом распределения , причем необходимо определить закон распределения первой. Задачу сформулировать можно следующим образом. Пусть задана функция g , осуществляющая отображение одной случайной величины X с заданным законом распределения в другую Y, то есть Y=g(X) . Требуется найти закон распределения случайной величины Y. Решение задачи начнем с дискретного случая. Пусть Х – дискретная случайная величина , имеющая ряд распределения:
-
Х
х1
x2
…
xn
р
p1
p2
…
pn
Тогда Y=g(X) – также дискретная случайная величина , принимающая значения
![]() ,
,
![]() , … ,
, … ,
![]() .
.
Если все значения
![]() - различны, то события
- различны, то события
![]() и
и
![]() для
для
![]() тождественны, а значит и
тождественны, а значит и
![]() и искомый ряд имеет вид
и искомый ряд имеет вид
-
Y
y1
y2
…
yn
р
p1
p2
…
pn
Если же среди чисел есть одинаковые, то их нужно отнести в таблице в один столбец, а соответствующие вероятности сложить.
Для непрерывной случайной величины
задача ставится следующим образом. Зная
плотность распределения случайной
величины Х и функцию отображения g(x)
, найти плотность распределения случайной
величины Y=g(X).
Пусть
![]() - плотность распределения случайной
величины Х и
- плотность распределения случайной
величины Х и
![]() - монотонная и дифференцируемая функция.
- монотонная и дифференцируемая функция.
Обозначим
![]() - плотность распределения вероятностей
с
- плотность распределения вероятностей
с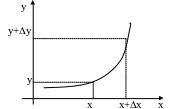 лучайной
величины Y. По определению
имеем
лучайной
величины Y. По определению
имеем
![]() .
.
Но вероятность попадания случайной
величины Y в интервал
![]() равна вероятности попадания случайной
величины Х в интервал
равна вероятности попадания случайной
величины Х в интервал
![]() ,
поэтому
,
поэтому

x = g-1(y),
где
![]() - обратная функция к функции
.
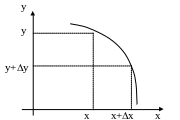
Если функция
- монотонно убывающая функция, то
приращению
- обратная функция к функции
.
Если функция
- монотонно убывающая функция, то
приращению
![]() соответствует приращение
соответствует приращение
![]() .
Следовательно,
.
Следовательно,

Пусть теперь y=g(x) функция такова, что обратная функция неоднозначна, то есть одному значению y соответствует несколько значений аргумента:
![]() ,
,
![]() ,…,
,…,
![]() ,
,
где n – число участков, на которых функция меняется монотонно.
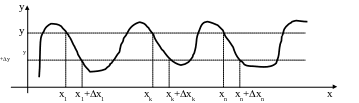
Очевидно,
что событие
![]() происходит при наступлении хотя бы
одного из несовместимых событий
происходит при наступлении хотя бы
одного из несовместимых событий
![]() ,
,
![]() ,…,
,…,
![]() .
Другими словами вероятность появления
события
равна вероятности события
.
Другими словами вероятность появления
события
равна вероятности события
+ +…+ . Поэтому
![]()
а значит
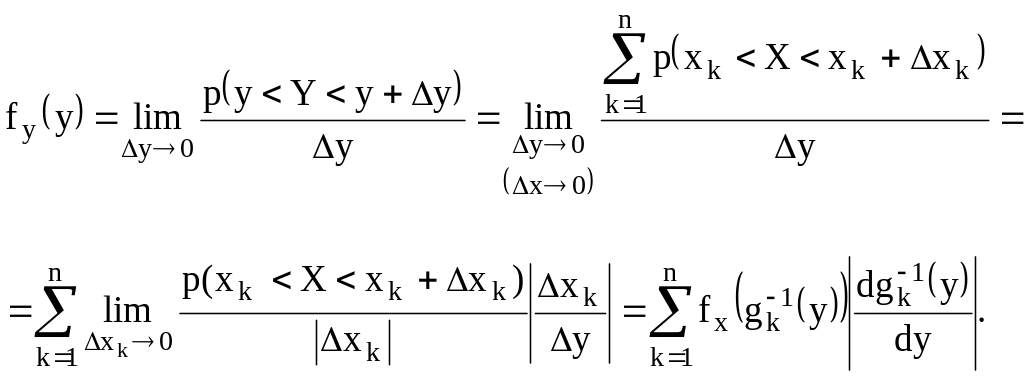
Здесь
![]() - обратная функция монотонной на k-том
участке функции
.
- обратная функция монотонной на k-том
участке функции
.
В
качестве примера рассмотрим следующую
ситуацию. Пусть приложенное к электрической
цепи напряжение или текущий через нее
ток носит случайный характер с гауссовским
законом распределения. Мощность,
рассеиваемая на активном сопротивлении,
представляет собой случайную величину
пропорциональную квадрату тока или
напряжения. Найти плотность распределения
вероятностей мощности. Пусть I
– случайная величина, соответствующая
значениям тока, а W=RI2
– мощность. Найдем обратную функцию
![]() ,
которая двузначная. Если обозначить
,
которая двузначная. Если обозначить
![]() - плотность распределения вероятностей
тока, то плотность распределения
вероятностей мощности
- плотность распределения вероятностей
тока, то плотность распределения
вероятностей мощности
![]() будет иметь вид
будет иметь вид
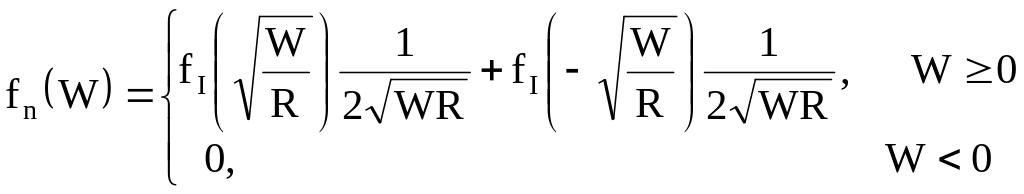
При
гауссовском законе распределения тока
I
с математическим ожиданием равным нулю
и дисперсией
![]() :
:
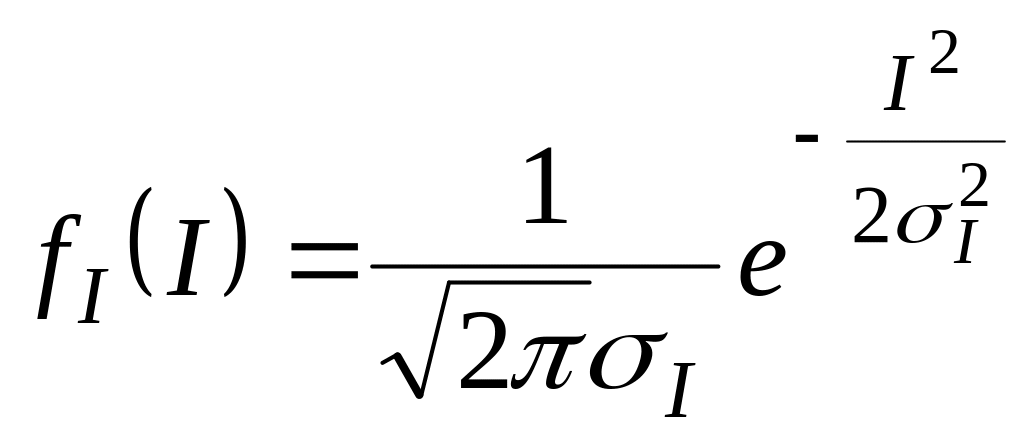
имеем
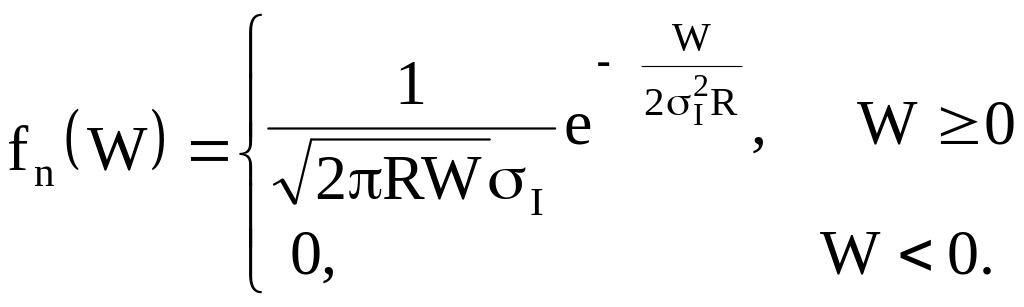
График этой функции имеет вид
fn(w)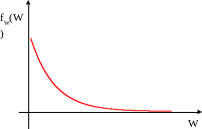
Числовые характеристики мощности легко определяются:
![]()
![]()
