1. Оценка параметров

По опытным данным (выборке) путем построения гистограммы или с помощью других средств можно попытаться построить вероятностную модель (определить закон распределения вероятностей). При этом выборочные данные позволяют уточнить детали вероятностной модели. Знание вероятностной модели дает возможность прогнозировать будущие события, что важно для принятия решений. В приложениях, как правило, относительные частоты, на что указывалось ранее, применяются только для грубой качественной оценки распределения генеральной совокупности. Обычно задаются определенным типом закона распределения генеральной совокупности (плотностью распределения)

f = f(x; a₁, a₂, ..., a_n)

и по данным случайной выборки (х₁, х₂, ..., х_n) оценивают неизвестные параметры a₁, a₂, ..., a_n . Чаще всего параметрами являются генеральное среднее и дисперсия. В качестве оценки тогда используют выборочные характеристики: выборочное среднее и выборочную дисперсию.

Рассмотрим следующую задачу. Пусть имеется случайная величина Х (генеральная совокупность), закон распределения которой содержит один неизвестный параметр а (например, f = f(x, a)). Требуется на основании выборочных данных (х₁, х₂, ..., х_n) найти подходящую оценку параметра а. С этой целью построим следующую модель. Пусть Х₁, Х₂, ..., Х_n – независимые случайные величины, которые принимают соответствующие выборочные значения (для данной выборки значения х₁, х₂, ..., х_n), и пусть случайная величина получена на основе случайных величин Х₁, Х₂, ..., Х_n, то есть Будем считать, как и ранее, что случайные величины Х₁, Х₂, ..., Х_n имеют один и тот же закон распределения с плотностью распределения вероятностей величины Х (генеральной совокупности) f(x). Тогда является случайной величиной, закон распределения которой зависит от n и от f(x). Для того, чтобы оценка имела практическую ценность она должна обладать следующими свойствами.

1. Несмещенность оценки. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру генеральной совокупности:

В противном случае оценка называется смещенной и допускает систематическую ошибку. Так рассмотренное ранее среднее выборочное является несмещенной оценкой среднего генерального. В то же время выборочная дисперсия

- является смещенной оценкой генеральной дисперсии.

2. Состоятельность оценки. Оценка называется состоятельной, если она с увеличением объема выборки сходится по вероятности к параметру генеральной совокупности:

Это условие будет выполняться, если

и оценка является несмещенной. Доказательство основано на неравенстве Чебышева.

3. Эффективность оценки. Если составлять множество несмещенных и состоятельных оценок, то эти оценки будут иметь разные дисперсии. Ясно, что, чем меньше будет дисперсия, тем меньше будет вероятность грубой ошибки при определении приближенного параметра генеральной совокупности. Поэтому нужно выбрать такую оценку, чтобы ее дисперсия была минимальной:

Такая оценка называется эффективной.

При обработке экспериментальных данных необходимо руководствоваться сформулированными свойствами оценок.

В качестве примера покажем, что рассмотренные ранее оценки: выборочное среднее и выборочная дисперсия , являясь несмещенными, являются и состоятельными оценками. Действительно, так как, согласно закону больших чисел

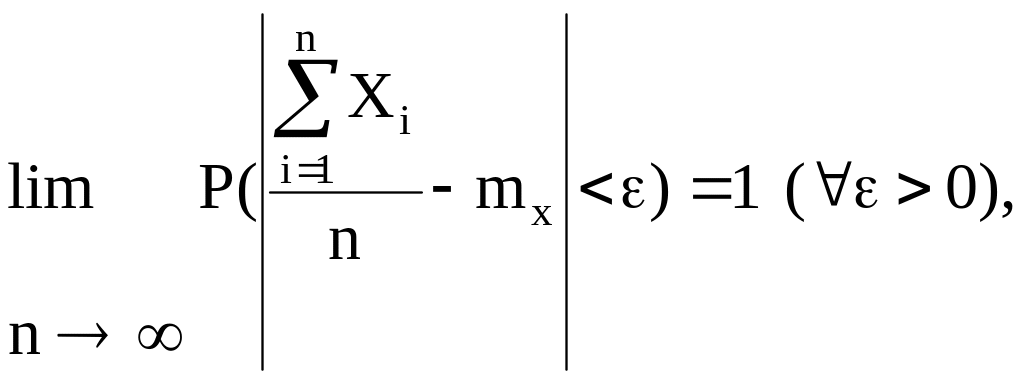
то выборочное среднее является состоятельной оценкой.

Для того, чтобы показать, что выборочная дисперсия является состоятельной оценкой, покажем вначале, что смещенная оценка - состоятельная оценка. С этой целью запишем:

(14.1)

При n  случайная величина стремится по вероятности к М(Х²), а выборочное среднее - к среднему генеральному m_x. Тогда из соотношения (14.1) следует, что при n  сходится по вероятности к величине М(Х²)-m_x²=D(X)=², которая является генеральной дисперсией. Тем самым доказана состоятельность оценки . Если теперь рассмотреть несмещенную оценку генеральной дисперсии то поскольку множитель стремится к единице при n , а стремится по вероятности к ², то и оценка стремится по вероятности к ², что доказывает состоятельность оценки .