
- •Лекция № 3 Введение. Классификация событий. Действия над событиями
- •2. События. Классификация событий. Пространство элементарных событий
- •4. Практические занятия
- •Лекция№5:Условная вероятность. Формула полной вероятности и формула Байеса. Независимые случайные события
- •1.1 Распределение Релея
- •1 Система двух случайных величин
- •1.Введение
- •4. Практические занятия
- •2.Элементы теории множеств.
- •2.1 Определение множества. Мощность множества. Подмножества.
- •2.2 Множества и подмножества.
- •2.3 Способы задания множеств. Универсальное множество.
- •2.4 Операции над множествами.
- •Практическое занятие №2
- •Тема: Основные понятия комбинаторики.
- •2. Перестановки, размещения.
- •3. Сочетания.
- •4. Разбиение на группы:
- •1. Введение
- •3. Алгебра событий
- •1. Введение
- •2. События. Классификация событий. Пространство элементарных событий
- •Примеры.
- •3. Алгебра событий
- •События Вi образуют полную группу событий, если
- •Особый интерес представляют полные группы несовместимых событий
- •План лекции:
- •2. Классический способ задания вероятностей.
- •3. Статистическая вероятность
- •4. Геометрическая вероятность.
- •Лекция№5
- •2. Формула полной вероятности.
- •3. Формула Байеса (теорема гипотез).
- •4. Независимые случайные события.
- •Контрольные вопросы и тесты
- •2 Закон распределения случайной величины.
- •3. Функция распределения
- •4. Плотность распределения случайной величины
- •Практическое занятие №1
- •1.Математическое ожидание , мода и медиана случайной величины
- •2. Моменты. Дисперсия. Среднее квадратическое отклонение.
- •3. Моменты высших порядков
- •Математическое ожидание, мода и медиана случайной величины
- •2. Моменты. Дисперсия. Среднее квадратическое отклонение.
- •3. Моменты высших порядков
- •Практическое занятие №1
- •5. Контрольные вопросы и задания
- •1. Биномиальное распределение
- •2. Распределение Пуассона
- •3. Простейший поток событий
- •1. Испытания (схема) Бернулли. Биномиальное распределение
- •Если ставить вопрос о появлении события а k-раз в n испытаниях в произвольном порядке, то событие представимо в виде
- •2. Распределение Пуассона.
- •3. Простейший поток событий
- •Задача 4
- •Задача 5
- •Задача 6
- •Практическое занятие № 2
- •5. Контрольные вопросы
- •1.1 Равномерное распределение вероятностей
- •1.2 Показательное (экспоненциальное) распределение
- •1.3 Нормальное распределение
- •Задача 1
- •Решение
- •Решение
- •Задача 4
- •Задача 6
- •Практическое занятие №2
- •2. Рекомендуемые фрагменты программ
- •1.1 Распределение Релея
- •1.1 Распределение Релея
- •1.2 Распределение Максвелла
- •1.3 Логарифмическое нормальное распределение
- •2. Функция случайной величины.
- •Практическое занятие №1
- •3. Рекомендации к выполнению.
- •Практическое занятие №2
- •Задача3
- •1 Система двух случайных величин
- •1 Система двух случайных величин
- •1.2 Плотность распределения двух случайных величин
- •1.3 Условные функция распределения и плотность распределения
- •1.4 Корреляция двух случайных величин
- •Аналогично имеем
- •2. Система произвольного числа случайных величин
- •Задача1
- •Практическое занятие №2 Тема: Исследование системы двух случайных величин
- •Так как под интегралом в (1) находится неотрицательная величина, то, выбросив из интервала интегрирования отрезок ав, мы значение интеграла не увеличим, т.Е.
- •2. Характеристические функции
- •Для дискретной случайной величины х с законом распределения
- •Свойства характеристической функции
- •3. Центральная предельная теорема
- •2. Числовые характеристики выборки
- •2.1. Выборочное среднее
- •Выборочная дисперсия
- •3. Статистический ряд. Статистическая функция распределения
- •4. Статистическая совокупность. Гистограмма
- •1. Оценка параметров
- •2. Метод наибольшего правдоподобия для нахождения оценок
- •3. Метод наименьших квадратов
Если ставить вопрос о появлении события а k-раз в n испытаниях в произвольном порядке, то событие представимо в виде
-
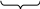
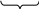
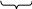 Bk
= AAA
Bk
= AAA
 +
+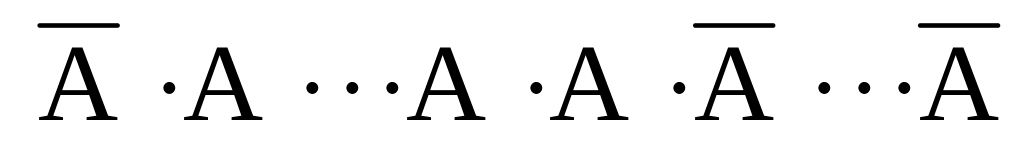 +
+
+
+


k n-k k n-k k n-k
Число различных слагаемых в правой
части этого равенства равно числу
испытаний из n по k
![]() ,
поэтому вероятность событий
,
которую будем обозначать
,
поэтому вероятность событий
,
которую будем обозначать
![]() ,
равна
,
равна
![]()
Последовательность
событий
![]() образует
полную группу независимых событий
образует
полную группу независимых событий
![]() .
Действительно, из независимости событий
получаем
.
Действительно, из независимости событий
получаем
![]()
Рассмотрим случайную величину Х – число появлений события А в n испытаниях. Она принимает значения 0,1,2…,к,…n. Но как известно, вероятность того, что событие А появится К раз в n испытаниях вычисляется по формуле Бернулли:
![]() (1)
(1)
Говорят,
что с.в. Х имеет биномиальное
распределение,
если ее возможные значения равны
0,1,2…,к, …n,
а соответствующие вероятности определяются
по формуле (1). . Это название связано с
тем, что
![]() равно коэффициенту при
равно коэффициенту при
![]() в
разложении бинома
в
разложении бинома
![]()
Возникает вопрос, какое максимальное значение принимает , если рассматривать , как функцию от k при фиксированном n? С этой целью рассмотрим отношение

Отсюда
следует, что
будет больше
![]() ,
если
,
если
![]() и меньше, если
и меньше, если
![]() .
Если
.
Если
![]() -
целое число, то Рn
(m)=Рn
(m-1). Это значит, что в двух точках
достигается максимальное по k
значение
.
Исключая эту ситуацию, имеем только
одно целое число m, которое заключено в
интервале
-
целое число, то Рn
(m)=Рn
(m-1). Это значит, что в двух точках
достигается максимальное по k
значение
.
Исключая эту ситуацию, имеем только
одно целое число m, которое заключено в
интервале
![]()
-
максимизирующее вероятность
 .
.n
Распределение
(1) зависит от двух параметров :![]() и
и
![]() .
.
Рассмотрим числовые характеристики с.в., распределенной по биномиальному закону.
Математическое
ожидание
числа появления события А в n
независимых испытаниях равно произведению
числа испытаний на вероятность появления
события в каждом испытании:
![]()
Очевидно, что общее число Х появлений события А в n испытаниях складывается из числа появления события А в отдельных испытаниях. Поэтому если Х1 число появлений события А в 1-м испытании, Х2 число появлений события А во 2-ом, Хn – в n -ом, то общее число появлений события А в n опытах будет равно:
![]()
Тогда
![]() ,
где
,
где
![]() -
математическое ожидание числа появления
события А в i
– ом опыте. Определим его
-
математическое ожидание числа появления
события А в i
– ом опыте. Определим его
![]()
Математическое ожидание числа появлений события в одном испытании равно вероятности этого события. Тогда
![]() .
.
Дисперсия
биномиального
распределения с параметрами
и
равна произведению
![]() .
.
![]() .
.
Доказательство.
По формуле дисперсии
![]() ;
;
Поскольку Х1, Х2,…Хn независимы, то можно записать.
![]()
Определим
![]()
![]() ;
;
![]() ;
с вероятностью
и
;
с вероятностью
и
![]() :
:
![]() ;
;
![]() ;
;
![]()
![]()
Пример:
Передается 5 сообщений по каналу связи.
Каждое сообщение с вероятностью
![]() независимо от других искажений. Случайная
величина Х – число искаженных сообщений.
Построим ряд распределения, определим
математическое ожидание, дисперсию,
среднеквадратичное отклонение
непосредственно по ряду
сравненим с теми, которые получены по
формулам.
независимо от других искажений. Случайная
величина Х – число искаженных сообщений.
Построим ряд распределения, определим
математическое ожидание, дисперсию,
среднеквадратичное отклонение
непосредственно по ряду
сравненим с теми, которые получены по
формулам.
Решение: Случайная величина Х – число искаженных сообщений распределена по биномиальному закону, под испытанием понимается “передача сообщения”, под “успехом“- его искажение. С. в. принимает значения 0,1,2,3,4,5.
Ряд распределения будет иметь вид:
0 |
1 |
2 |
3 |
4 |
5 |
0,168 |
0,360 |
0,309 |
0,133 |
0,028 |
0,02 |
![]() ;
;![]() ;
;
![]()
![]() ;
;
![]()
График распределения с параметрами n=5,p=0,3; k=0,1,2,3,4,5 представлен на рис.8.1

Рисунок 8.1 –Биномиальное распределения
