2. Моменты. Дисперсия. Среднее квадратическое отклонение.

Кроме характеристик положения в теории вероятностей употребляется еще ряд числовых характеристик различного назначения; каждая из них характеризует с.в. с точки зрения тех или иных особенностей ее распределения. Среди них особое значение имеют моменты – начальные и центральные.

Начальным моментом S-го порядка с.в. Х называется математическое ожидание S-ой степени этой величины

Для дискретной с.в .Х начальный момент S-го порядка выражается суммой

, для непрерывной - интегралом

, где - плотность распределения.

Ранее введенная характеристика - есть не что иное, как первый начальный момент

.

Прежде чем дать определение центрального момента, введем новое понятие “центрированной с.в.”. Центрированной с.в .Х называют отклонение с.в. от её математического ожидания, т.е.

.

Нетрудно убедиться, что математическое .ожидание центрированной с.в.= 0.

Центрирование с.в. равносильно переносу начала отсчета в т. (центр распределения).

Моменты центрированной с.в. называются центральными моментами. Центральным моментом S-го порядка с.в.Х называется математическое ожидание S-ой степени центрированной с.в.

;

Для дискретной с.в. , для непрерывной- .

Очевидно, что для любой с.в.Х центральный момент 1-го порядка равен 0.

Особое значение на практике имеет второй центральный момент, он называется дисперсией с.в. Ввиду крайней важности его среди других для него введено специальное обозначение или .

Согласно определению центрального момента

.

Дисперсией случайной величины Х называется математическое ожидание квадрата отклонения величины от ее математического ожидания:

Для непосредственного вычисления дисперсии служат формулы:

а) для дискретной с.в.

б) для непрерывной с.в.

На практике часто бывает проще вычислить 2-ой начальный момент, чем дисперсию и тогда для вычисления дисперсии пользуются формулой:

;

Из определения получаем что:

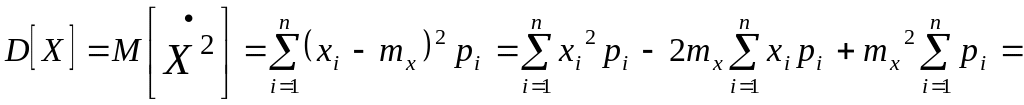
Таким образом мы получили, что дисперсия равна математическому ожиданию квадрата случайной величины минус квадрат математического ожидания.

Дисперсия имеет размерность квадрата случайной величины Х, а удобно иметь характеристику разброса случайной величины относительно своего среднего значения такой же размерности как Х. С этой целью вводят среднее квадратичное отклонение случайной величины Х, обозначаемое , как

.

Эту величину еще называют стандартным отклонением. Для неотрицательной с.в.Х в качестве характеристики применяется коэффициент вариации, равный отношению с.к.о. к мат.ожиданию

Свойства дисперсии.

1. Дисперсия постоянной величины равна нулю: ,

что очевидно, т.к. .

2. Постоянный множитель выносится за знак дисперсии в квадрате:

.

Действительно,

3. Дисперсия суммы двух независимых случайных величин X и Y равна

сумме дисперсий:

4)

5) ;

Действительно,

В электрических приложениях дисперсия, как правило, соотносится со средней мощностью, выделяемой на активном сопротивлении переменной составляющей приложенного к нему напряжения или тока, а корень квадратный из дисперсии в этом случае будет соответствовать показанию вольтметра или амперметра.