План лекции:

1.Аксиоматический способ задания вероятностей

2. Классический способ задания вероятностей

3. Статистическая вероятность

4. Геометрический способ задания вероятностей

1.Аксиоматический способ задания вероятностей

Рассмотрим эксперимент, с конечным или счетным числом возможных исходов

={₁, ₂, _i… }.Предположим, что каждому элементарному событию _i приписан некоторый ''вес'' p_i, называемый вероятностью появления элементарного события _i , и потребуем,чтобы вероятность p_i удовлетворяла следующим условием:

1. 0p(_i)1 (неотрицательность)

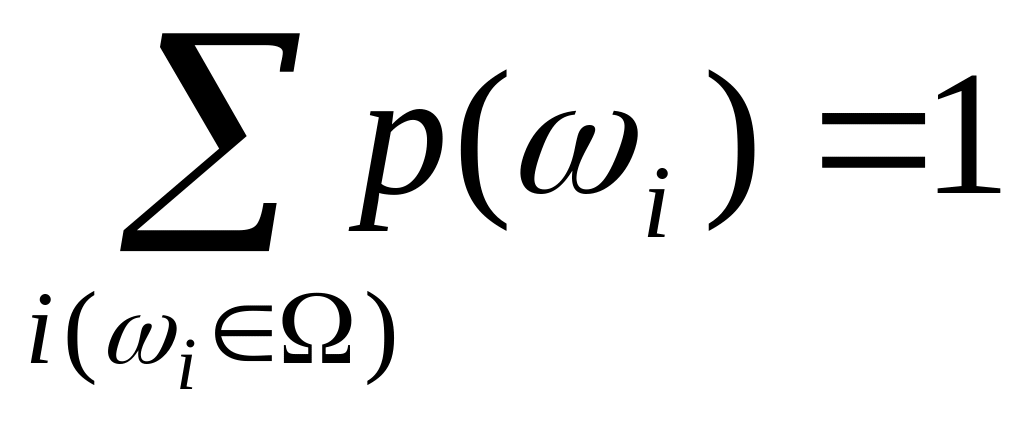2. ; (нормированность).

Для данного эксперимента построена вероятностная модель, если указано пространство элементарных событий  : ; и известна вероятность элементарного события Р(_i), Р_i 0; ,_i.

Пусть А – произвольное случайное событие, наблюдаемое в данном эксперименте т.е. А   . Тогда имеет место следующее определение.

Определение: Вероятностью события А называют сумму вероятностей элементарных событий, составляющих событие А:

.

Из определения вероятности события P(A) вытекают следующие свойства вероятности:

1. 0P(A); - аксиома неотрицательности;

2. P()=1; - аксиома нормировки;

3. Аксиома аддитивности (сложения):

Если А и В несовместнимые события (А   , В   ,АВ= ), то Р(А+В)=Р(А)+Р(В).

Эти аксиомы были сформулированы А.Н.Колмогоровым и оказали огромное влияние на развитие теории вероятностей. Такое задание вероятности события называются аксиоматическим.

Аксиома аддитивности может быть расширена на случай n попарно несовместимых событий, т.е.

, A_i ; A_iA_j=; i,j= , ij.

Вероятность суммы несовместимых событий равна сумме вероятностей этих событий.

Аксиому сложения вероятностей иногда называют теоремой сложения вероятностей, или правилом сложения вероятностей.

Если имеется счетное множество несовместимых событий А₁,А₂…Аn… (A_iA_j=; ij), то ;

Следствия из аксиом теории вероятностей:

Следствие 1: Если А  В (А влечет В), то Р(А)<Р(В).

Следствие 2: Р( )=1- Р(А); А+ = ;( по аксиоме 3, А =).

Р(А)+Р( )=Р(А+ )=Р()=1;

Следствие 3: Р()=0;

Следствие 4: Если А и В совместимые события, наблюдаемые в одном и том же пространстве элементарных событий , тогда

Р(А+В)=Р(А)+Р(В) - Р(АВ).

Замечание 1: Если имеется три совместных события А,В,С, связанных с одним и тем же испытанием, то можно показать, что

Р(А+В+С)=Р(А)+Р(В)+Р(С)-Р(АВ)-Р(АС)-Р(ВС)+Р(АВС).

Замечание 2: Вероятность суммы событий в случае, когда число слагаемых больше 2-х, целесообразно вычислять переходом к противоположному по отношению к сумме событию.

Вывод: Аксиомы теории вероятностей позволяют вычислять вероятности любых случайных событий через вероятности элементарных событий, если их число конечно или счетно. Но теория вероятностей ''не учит'' тому, как правильно определять вероятности элементарных событий. На практике они определяются либо непосредственно по условиям опыта (если он обладает симметрией возможных исходов), либо на основе экспериментальных статистических данных, (если он такой симметрией не обладает).

Примеры:

1.Бросают симметричную шестигранную игральную кость: ={1,2,3,4,5,6}: Р(_i)=1/6; А={2,4,6}; Р(А)=1/6+1/6+1/6=3/6=1/2;

2. Предположим, что игральная кость не симметрична, и масса каждой грани пропорциональна его номеру т.е. р(_i)=Р_i=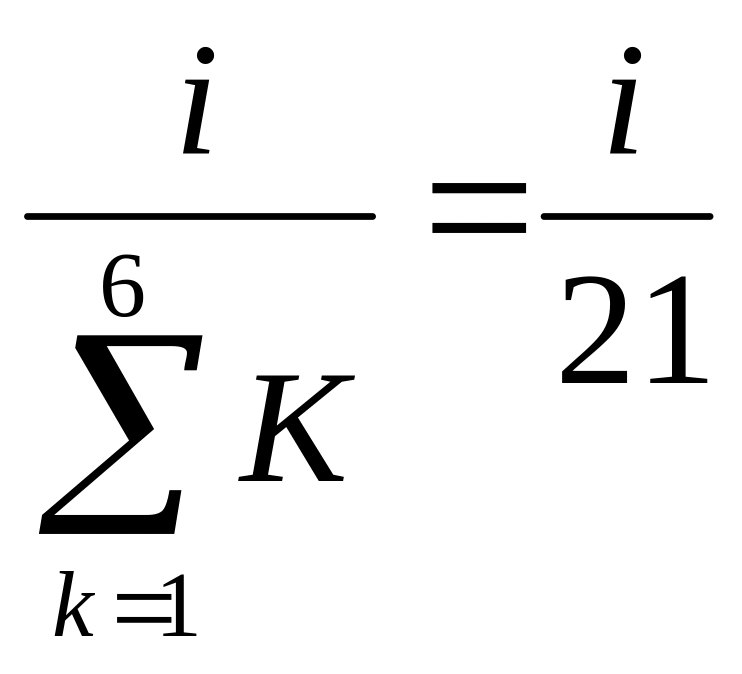 ; Тогда вероятность события А Р(А)=2/21+4/21+6/21=12/21;

3. Пусть симметричная монета подбрасывается до тех пор, пока впервые не появится герб. Тогда ={₁,₂,.._n,…,_}, где n= , будет проведено n подбрасываний. _ - элементарное событие, обозначающее что герб никогда не появится. Припишем _n вероятность ; Р(_n)= ; Р(_)=0. Тогда ;

Подсчитаем вероятность события А, состоящего в том, что будет проведено не более 3-х подбрасываний монеты, до выпадения герба,

А={Г,РГ,РРГ},Р(А)=1/2+1/4+1/8=7/8;