2.2 Множества и подмножества.

Определение: Множество В, все элементы которого являются элементами множества А называются подмножеством, (частью) множества А Это отношение между множествами называют включением и обозначают символом ,т.е. В А..

Подмножеством любого множества является пустое множество Ǿ А.

Любое непустое множество А имеет, по крайней мере, два различных подмножества: само А и пустое множество Ǿ. Эти подмножества называются несобственными, а все другие подмножества называются собственными. Эта терминология связана не со словом «собственность», а со словом «собственно». Конечные собственные подмножества образуют всевозможные сочетания по одному, два, три и т. д. элементов данного множества. Множество, элементами которого являются все подмножества множества А, называют множеством подмножеств (множеством-степенью) и обозначают через (А). Для трехэлементного множества А= (А)= . Если =n, . Если множество А конечно, то оно имеет точную верхнюю границу:

sup A= ;

и точную нижнюю границу:

inf A=min ,

Если бесконечное множество А имеет точную верхнюю границу М, то оно ограничено сверху, если имеет нижнюю границу, то оно ограничено снизу. Примером таких множеств являются интервалы—

1) , ;

2) , [ + );

3) (- , ].

2.3 Способы задания множеств. Универсальное множество.

Множество может быть задано следующими способами: списком его элементов, порождающей процедурой и описанием свойств его элементов.

I. Списком могут быть заданы только конечные множества. Список обычно заключается в фигурные скобки, например ; этот способ не пригоден для задания бесконечных множеств и даже в случае конечных множеств не всегда практически реализуем.

II. Порождающая процедура описывает способ получения элементов множества из уже полученных элементов; используется для задания бесконечных и конечных множеств. Например, множество порождающая процедура для которого определяется следующими двумя правилами:

1) ;

2) если то .

Правила, описанные таким образом называются индуктивными или рекурсивными.

III. Задание множества описанием свойств его элементов, пожалуй, наиболее обычно. В случае, когда свойство элементов множества М может быть описано коротким выражением ρ(х), множество М задания при помощи обозначается:

М={х ρ(х)}, которое читается так: М – это множество элементов х, обладающих свойством ρ. Вместо вертикальной черты часто используется двоеточие. ρ(х) –это либо высказывание, в котором что-либо утверждается об х, либо это некоторая функция переменной х, например:

а) М₂n={х х=2^К}, где к N;

б) множество S точек на числовой оси, расстояние от которых до точки с абсциссой а не превосходит d:

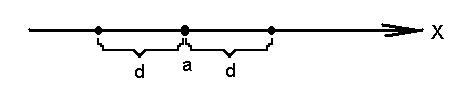
S={|x-a| d} или S={x:|x-a| d}, где х – абсцисса точки.

в) Множество С точек на плоскости, лежащих внутри или на границе круга радиуса r с центром в начале координат может быть задано в виде:

С={x­­­­²+y² r²} или С={(x,y):(x­­­­²+y² r²)}, где х,y – декартовы координаты точки.

С помощью указанных средств не возможно сконструировать все возможные множества. Вопрос задания множеств является сложным вопросом. Но с помощью указанных способов мы сможем сконструировать все множества, которые будут использованы в данном курсе.

Уже в самом задании конкретного множества явно или неявно ограничивается совокупность допустимых объектов. Так например, множество чисел, делящихся на 3 следует искать во множестве целых чисел, так же множество слонов среди млекопитающих, а не планет, множество абонентских станций оконечных устройств систем связи и т.д..

Удобно совокупность допустимых объектов, т.е. объектов данной природы (обладающих определенными свойствами) зафиксировать явным образом, и считать, что рассматриваемые множества являются подмножествами этой совокупности. Эту совокупность называют основным множеством (универсумом) и обозначают буквой U. Так универсумом арифметики служат числа, лингвистики – слова, в теории связи – сигналы. Так можно выделить множество непрерывных и дискретных сигналов, множество сигналов тональной частоты и т.д..

Универсальное множество, это множество, объединяющее элементы всех множеств рассматриваемого класса задач.