
- •Лекция № 3 Введение. Классификация событий. Действия над событиями
- •2. События. Классификация событий. Пространство элементарных событий
- •4. Практические занятия
- •Лекция№5:Условная вероятность. Формула полной вероятности и формула Байеса. Независимые случайные события
- •1.1 Распределение Релея
- •1 Система двух случайных величин
- •1.Введение
- •4. Практические занятия
- •2.Элементы теории множеств.
- •2.1 Определение множества. Мощность множества. Подмножества.
- •2.2 Множества и подмножества.
- •2.3 Способы задания множеств. Универсальное множество.
- •2.4 Операции над множествами.
- •Практическое занятие №2
- •Тема: Основные понятия комбинаторики.
- •2. Перестановки, размещения.
- •3. Сочетания.
- •4. Разбиение на группы:
- •1. Введение
- •3. Алгебра событий
- •1. Введение
- •2. События. Классификация событий. Пространство элементарных событий
- •Примеры.
- •3. Алгебра событий
- •События Вi образуют полную группу событий, если
- •Особый интерес представляют полные группы несовместимых событий
- •План лекции:
- •2. Классический способ задания вероятностей.
- •3. Статистическая вероятность
- •4. Геометрическая вероятность.
- •Лекция№5
- •2. Формула полной вероятности.
- •3. Формула Байеса (теорема гипотез).
- •4. Независимые случайные события.
- •Контрольные вопросы и тесты
- •2 Закон распределения случайной величины.
- •3. Функция распределения
- •4. Плотность распределения случайной величины
- •Практическое занятие №1
- •1.Математическое ожидание , мода и медиана случайной величины
- •2. Моменты. Дисперсия. Среднее квадратическое отклонение.
- •3. Моменты высших порядков
- •Математическое ожидание, мода и медиана случайной величины
- •2. Моменты. Дисперсия. Среднее квадратическое отклонение.
- •3. Моменты высших порядков
- •Практическое занятие №1
- •5. Контрольные вопросы и задания
- •1. Биномиальное распределение
- •2. Распределение Пуассона
- •3. Простейший поток событий
- •1. Испытания (схема) Бернулли. Биномиальное распределение
- •Если ставить вопрос о появлении события а k-раз в n испытаниях в произвольном порядке, то событие представимо в виде
- •2. Распределение Пуассона.
- •3. Простейший поток событий
- •Задача 4
- •Задача 5
- •Задача 6
- •Практическое занятие № 2
- •5. Контрольные вопросы
- •1.1 Равномерное распределение вероятностей
- •1.2 Показательное (экспоненциальное) распределение
- •1.3 Нормальное распределение
- •Задача 1
- •Решение
- •Решение
- •Задача 4
- •Задача 6
- •Практическое занятие №2
- •2. Рекомендуемые фрагменты программ
- •1.1 Распределение Релея
- •1.1 Распределение Релея
- •1.2 Распределение Максвелла
- •1.3 Логарифмическое нормальное распределение
- •2. Функция случайной величины.
- •Практическое занятие №1
- •3. Рекомендации к выполнению.
- •Практическое занятие №2
- •Задача3
- •1 Система двух случайных величин
- •1 Система двух случайных величин
- •1.2 Плотность распределения двух случайных величин
- •1.3 Условные функция распределения и плотность распределения
- •1.4 Корреляция двух случайных величин
- •Аналогично имеем
- •2. Система произвольного числа случайных величин
- •Задача1
- •Практическое занятие №2 Тема: Исследование системы двух случайных величин
- •Так как под интегралом в (1) находится неотрицательная величина, то, выбросив из интервала интегрирования отрезок ав, мы значение интеграла не увеличим, т.Е.
- •2. Характеристические функции
- •Для дискретной случайной величины х с законом распределения
- •Свойства характеристической функции
- •3. Центральная предельная теорема
- •2. Числовые характеристики выборки
- •2.1. Выборочное среднее
- •Выборочная дисперсия
- •3. Статистический ряд. Статистическая функция распределения
- •4. Статистическая совокупность. Гистограмма
- •1. Оценка параметров
- •2. Метод наибольшего правдоподобия для нахождения оценок
- •3. Метод наименьших квадратов
1.Математическое ожидание , мода и медиана случайной величины
2. Моменты. Дисперсия. Среднее квадратическое отклонение.
3. Моменты высших порядков
Математическое ожидание, мода и медиана случайной величины
На практике знание закона распределения случайной величины, как правило, является избыточным. Чаще всего в инженерной практике возникает необходимость в знании числовых характеристик случайной величины. Среди числовых характеристик случайной величины прежде всего рассмотрим характеристики положения, фиксирующие положение случайной величины на числовой оси, к которым относятся математическое ожидание, мода и медиана.
Рассмотрим
дискретную случайную величину. Пусть
дискретная случайная величина X принимает
значения
![]()
![]() и вероятность принятия случайной
величиной значения
и вероятность принятия случайной
величиной значения
![]() равна
равна
![]() .
Интуитивно ясно, что при наблюдении
случайной величины X в n (n>>1) повторных
независимых экспериментах значение
появится примерно
.
Интуитивно ясно, что при наблюдении
случайной величины X в n (n>>1) повторных
независимых экспериментах значение
появится примерно
![]() раз. Таким образом, среднее значение
этой величины , подсчитанное по n
экспериментам , есть примерно
раз. Таким образом, среднее значение
этой величины , подсчитанное по n
экспериментам , есть примерно
![]() .
.
Поэтому математическим ожиданием или средним значением дискретной случайной величины X называется число
![]() .
.
Если
![]() и ряд
и ряд
![]() сходится абсолютно, математическим
ожиданием является величина
сходится абсолютно, математическим
ожиданием является величина
![]() .
.
Можно
дать механическую интерпретацию
математического ожидания. Если в точки
прямой линии с абсциссами
положены соответственно массы
![]() ,
то с учетом , что
,
то с учетом , что
![]() ,
есть абсцисса центра тяжести этой
системы материальных точек. С позиции
математики математическое ожидании
является линейным функционалом, т.е.
линейной операцией, ставящей в соответствие
функции X() число
M(X).
,
есть абсцисса центра тяжести этой
системы материальных точек. С позиции
математики математическое ожидании
является линейным функционалом, т.е.
линейной операцией, ставящей в соответствие
функции X() число
M(X).
Сформулируем основные свойства математического ожидания.
если
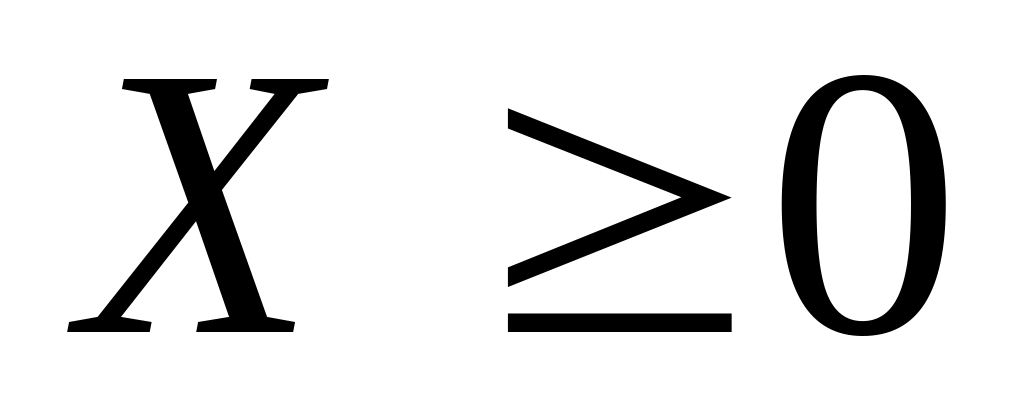 ,
то
,
то
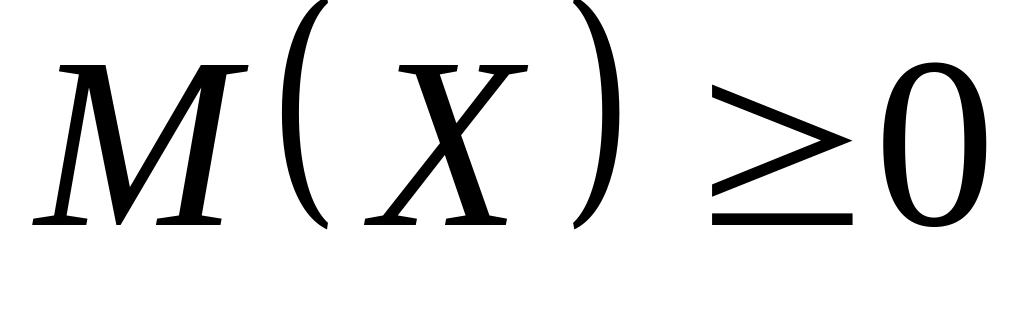 .
.Математическое ожидание постоянной величины равно самой постоянной:
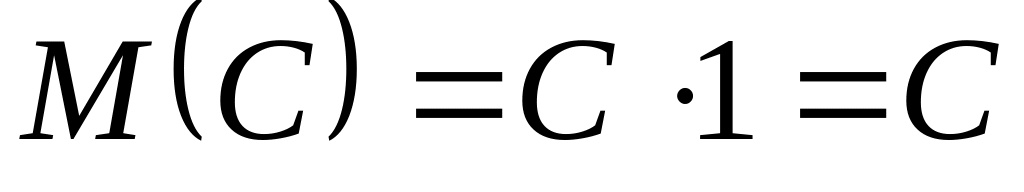 .
.Постоянный множитель можно выносить за знак математического ожидания:
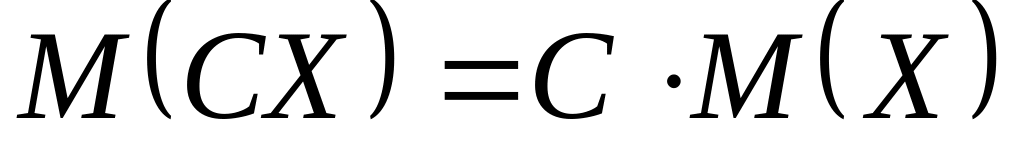 .
.
Действительно,
![]() .
.
Математическое ожидание от суммы случайных величин X и Y равно сумме математический ожиданий:
![]()
Свойства 2), 3) определяют линейность операции математического ожидания.
Если
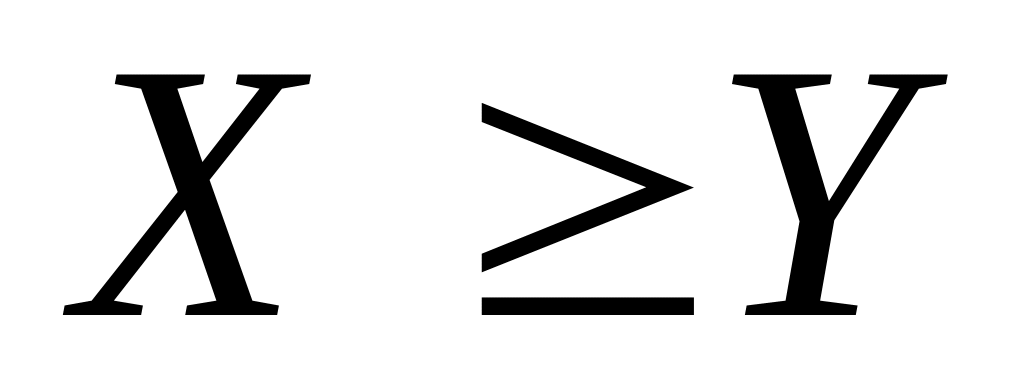 ,
то
,
то
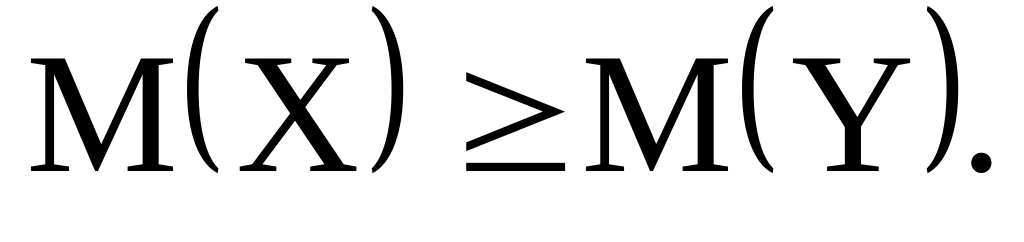
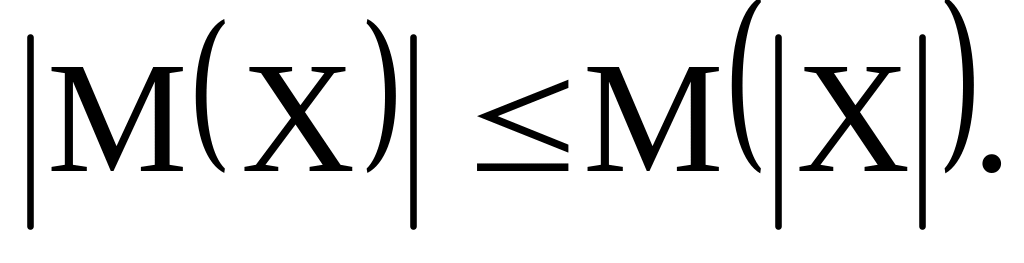
Свойства 5), 6) очевидны.
Если случайные величины X и Y независимы, то
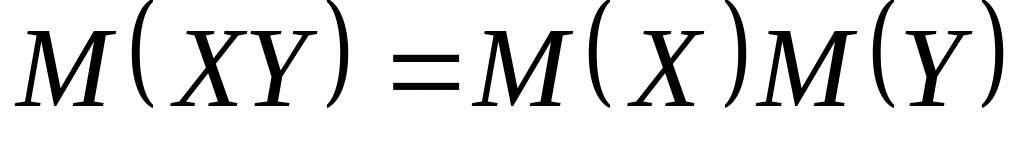
Пример. Изделия испытываются на надежность. Вероятность выхода из строя изделия за время испытания для каждого изделия равна р. Испытания заканчиваются, если изделие вышло из строя. Найти математическое ожидание числа испытаний.
Решение. Пусть Х – число испытаний. Ряд распределения случайной величины Х имеет вид:
-
X
1
2
3
…
k
…
p
p
qp
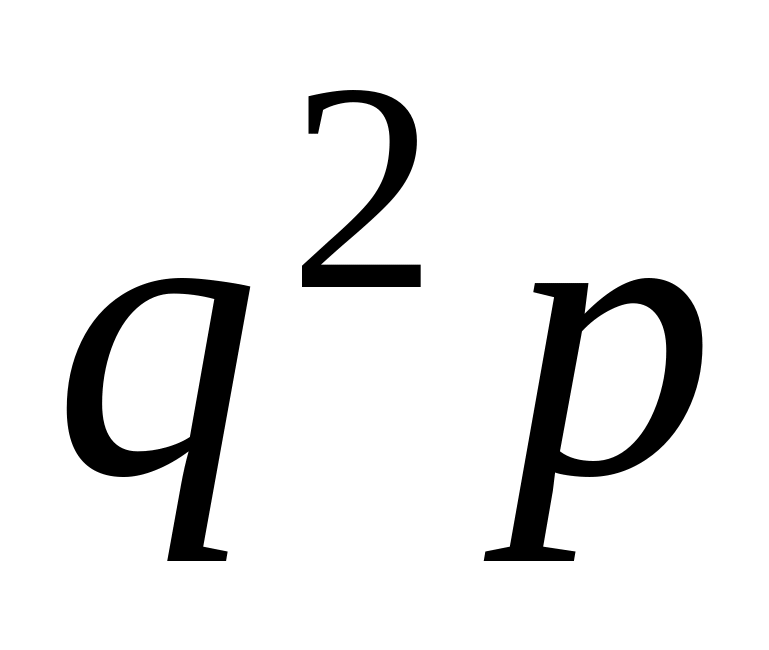
…
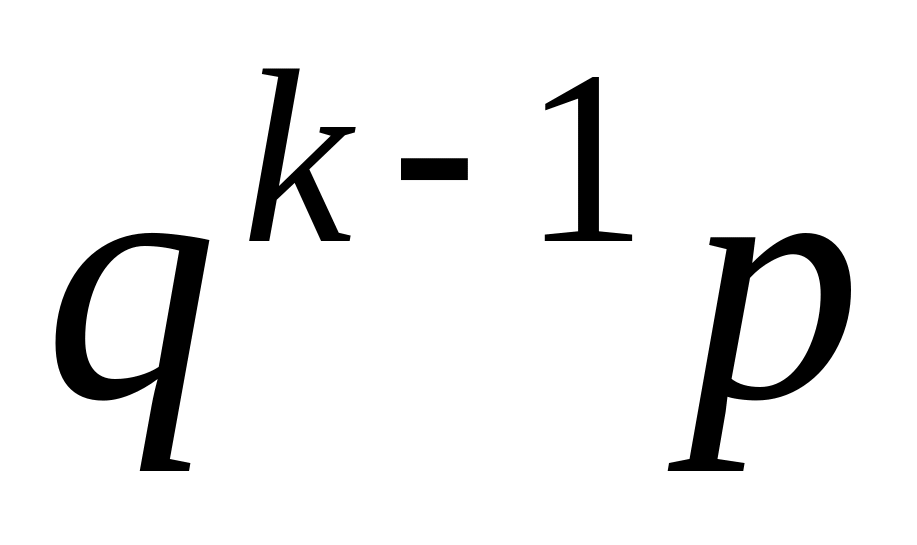
…
где
q+p=1. По определению
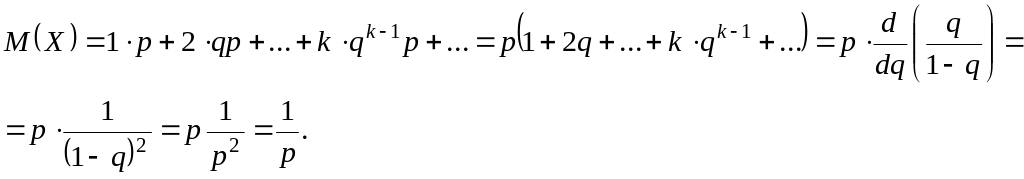
С
помощью введенной плотности распределения
вероятностей легко получить математическое
ожидание для непрерывной случайной
величины. Действительно, разбив интервал
изменения случайной величины на
маленькие интервалы
![]()
![]() и, так как приближенно
и, так как приближенно
![]() равно вероятности того, что случайная
величина Х примет значение
равно вероятности того, что случайная
величина Х примет значение
![]() , то можно для непрерывной случайной
величины Х математическое ожидание
записать в виде
, то можно для непрерывной случайной
величины Х математическое ожидание
записать в виде
![]() .
.
Правая
часть этого выражения представляет
интегральную сумму, поэтому, переходя
к пределу
![]() ,
получаем
,
получаем
![]() .
.
Математическое ожидание – не единственная характеристика положения;
иногда применяются и другие: мода и медиана с.в.
Определение.
Модой с.в. называется наиболее вероятное
значение с.в., т.е. для которого вероятность
![]() или плотность распределения
или плотность распределения
![]() достигает максимума.
достигает максимума.
Моду
обычно обозначают
![]() .
Экспериментальные аналоги моды:
для дискретной с.в.Х – то значение,
которое в данной серии опытов встречается
чаще всего; для непрерывной с.в. – центр
того элементарного интервала, для
которого плотность частоты
(отношение частоты попадания в этот
интервал к его длине) достигает максимума.
.
Экспериментальные аналоги моды:
для дискретной с.в.Х – то значение,
которое в данной серии опытов встречается
чаще всего; для непрерывной с.в. – центр
того элементарного интервала, для
которого плотность частоты
(отношение частоты попадания в этот
интервал к его длине) достигает максимума.
Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, то такое распределение называют полимодальным. Наличие более чем одной моды часто указывает на разнородность исследуемого статистического материала.
Еще
одной характеристикой
положения
– является медиана,.
Которую обычнообозначают
![]() .Эта
характеристика применяется, как правило,
для непрерывных случайных величин.
Медианой
непрерывной случайной величины Х
называется такое её значение
,
для которого
.Эта
характеристика применяется, как правило,
для непрерывных случайных величин.
Медианой
непрерывной случайной величины Х
называется такое её значение
,
для которого
![]() .
.
Геометрически
медиана – это абсцисса той точки на оси
![]() ,
для которой площади лежащие слева и
справа от нее, одинаковы и равны 1/2.
,
для которой площади лежащие слева и
справа от нее, одинаковы и равны 1/2.
В случае симметричного распределения, имеющего моду, математическое ожидание (если оно существует), мода и медиана совпадают.
