2. Формула полной вероятности.

Следствием обоих основных правил теории вероятности (правила сложения и правила умножения) – является формула полной вероятности.

Допустим, что предполагается провести опыт, об условиях которого можно сделать n исключающих друг друга предположений (гипотез).

Пусть гипотезы H₁, H₂,… , H_n образуют полную группу попарно несовместимых событий, т.е.

= H₁+ H₂+… + H_n (H_i H_j=0, ij).

Каждая гипотеза осуществляется случайным образом и представляет собой некоторое событие. Вероятности гипотез известны и равны Р(H₁),Р(H₂),…,р(H_n).

Рассматривается некоторое событие А, которое может проявиться только вместе с одной из гипотез , заданы условные вероятности Р(А/Нi) события А при каждой из гипотез. Требуется найти вероятность события А. Представим событие А следующим образом:

А=А=А(H₁+ H₂+… + H_n)= АH₁+ АH₂+… + АH_n.

Так как события АH₁, АH₂,… , АH_n также несовместимы, то используя правила сложения и умножения вероятностейЮ, получим формулу полной вероятности:

Р(А) = р(АH₁)+р(АH₂)+…+р(АH_n)=р(А/H₁)р(В₁)+р(А/H₂)р(H₂)+…+ р(А/В_n)р(В_n),

.

Безусловная вероятность события А в опыте с гипотетическими условиями вычисляется как сумма произведений вероятностей каждой гипотезы на условную вероятность события А при этой гипотезе.

Формула полной вероятности применяется во всех случаях, когда опыт со случайным исходом распадается на два этапа: в первом как бы ''разыгрываются'' условия опыта; во втором – его результат.

Пример: Среди N экзаменационных билетов n счастливых. Студенты подходят за билетами один за другим. У кого больше вероятность взять счастливый билет: у того, кто подошел первым, или у того кто подошел вторым?

Решение: Вероятность взять счастливый билет для первого студента равна, очевидно Р(А_i) =

А₁ – первый студент взял счастливый билет,

А₂ – второй студент взял счастливый билет,

Р(А₁) = ;

Вычислим Р(А₂). Можно сделать два предположения:

Н₁ – первый студент взял счастливый билет,

Н₂ – первый студент не взял счастливый билет. Н₁ +Н₂ =  ; Н₁ Н₂=.

Тогда по форме полной вероятности:

Р(А₂)= Р(H₁)  Р(А₂/H₁) + Р(H₂)  Р(А₂/H₂);

Определим Р(А₂/H₁) и Р(А₂/H₂);

;

H₁+ H₂=;

=n/N;

3. Формула Байеса (теорема гипотез).

Следствием правил умножения и формулы полной вероятности является теорема гипотез или формула Байеса.

Представим себе следующую ситуацию. До опыта о его условиях можно было сделать ряд гипотез Н1, Н2,…,Нn, несовместимых и образующих полную группу

; (ij);

Вероятность гипотез до опыта (априорные вероятности) заданы и равны: Р(H₁), Р(H₂),…, Р(H_n); ;

Теперь предположим, что опыт произведен, и в его результате появилось событие А. Спрашивается, как нужно пересмотреть вероятность гипотез, с учетом этого факта. Т.е. необходимо найти ''апостериорные вероятности'' гипотез, при условии, что опыт дал результат А, т.е Р(Н₁/А); Р(Н₂/А)… Р(Н_i/А).

Решим эту задачу, используя правило умножения и формулу полной вероятности:

Возьмем любую гипотезу Н_i и вычислим вероятность Р(Н_iА) по правилу умножения в двух формах:

Р(H_iA)= Р(H_i) Р(A/H_i)=P(A) Р(H_i/A);

Р(H_i) Р(A/H_i)=P(A) Р(H_i/A).

Разделим обе части на Р(А)0, т.е. .

Заменим Р(А) его выражением из формулы полной вероятности, получим формулу Байеса:

.

Пример: В урне находится n шаров. Возможно (n+1) гипотеза о количестве белых шаров в урне: Н₀, Н₁, Н₂,…,Нn. (Нi - гипотеза, состоящая в том, что в урне i белых шаров). Предположим, что все эти гипотезы одинаково возможны, т.е.

;

Из урны наугад взяли шар, который оказался белый. Пусть В – событие состоящее в том, что наугад взят шар – белый. Вычислим Р(Н_i/В).

Имеем ; (в урне i – белых шаров) по формуле классической вероятности.

Тогда по формуле Байеса:

;

;

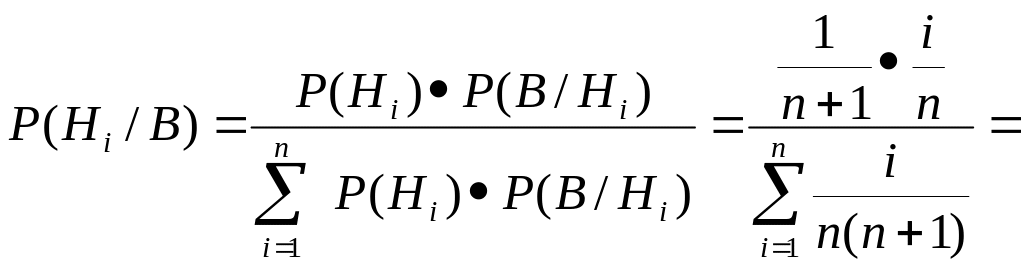
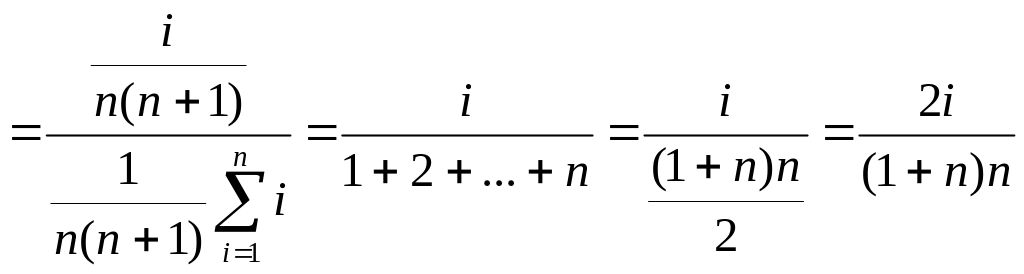Наиболее вероятной является гипотеза Нn.