2. Классический способ задания вероятностей.

Если элементарное событие i равнозначны, т.е. Р(i)=Р, (i имеют одинаковый вес) и А={_i1,_i2,…,_im}, iI, ={₁,₂,…,_n}, то Р()= ;

тогда Р(_i)=Р1/n; и Р(А)= .

При классическом подходе к определению вероятности вероятность события А можно трактовать как отношение исходов (элементарных событий), благоприятствующих появлению события А, к общему числу равнозначных исходов. Классическое определение вероятностей оправдано тогда, когда на основании симметрии, однородности и т.п. можно говорить о равнозначных исходах или равнозначных событиях.

Пример 1:

Выбирается наугад 4-х значный номер из цифр 0,1,…,9. Какова вероятность события А, состоящего в том, что этот номер содержит три данных цифры?

Решение. Вычислим вероятность противоположного события , состоящего в том, что номер не содержит ни одной из трех данных цифр. Число всевозможных номеров равно ^k_n=10⁴=n^k. Число номеров, не содержащих ни одной из трех данных цифр (10-3)⁴=7⁴;

Р( )=7⁴/10⁴=(7/10)⁴; (0,7)⁴;

Р(А)=1-Р( )=1-(0,7)⁴0,76;

3. Статистическая вероятность

Наряду с классическим определением вероятности, которое базируется на понятии «равнозначности события» и применимо к конечному числу элементарных событий, используется понятие статистической вероятности. В качестве статистической вероятности принимают частоту появления события А при проведении многократных испытаний. Пусть в результате n (n>>1) испытаний событие А появилось m раз, тогда статистическая вероятность

.

Из определения вытекают свойства:

, , , .

Английский математик Пирсон бросал монету 24000 раз. «Герб» выпадал 12012 раз, а значит статистическая вероятность выпадения «герба» (событие А) была равной

.

Недостаток этого определения при всей его привлекательности заключается в неоднозначности этого определения, т.е. в зависимости вероятности от числа испытаний. Другой статистический подход в определении вероятности заключается в том , что в качестве вероятности берут предел частоты появления события А при неограниченном числе испытаний:

.

Однако такой подход трудно реализовать на практике, так как невозможно произвести бесконечное число испытаний.

4. Геометрическая вероятность.

Если число равновозможных элементарных событий бесконечно, то использовать классическое определение вероятности невозможно. Однако, в таких ситуациях иногда можно воспользоваться методом геометрической вероятности. Суть метода заключается в случайном бросании точки на ограниченный участок либо прямой, либо плоскости, либо пространство. Если брошенная точка обязательно попадет в ограниченную область  , содержащую область А (А   ), и вероятность попадания в любую часть  не зависит от формы этой части и пропорциональна её мере (длине, площади, объему), то вероятность попадания точки в область А равна отношению мер областей А и  :

.

Пример: Стержень единичной длины произвольным образом разламывается на три части: x,y,z (x+y+z=1). Найти вероятность того, что из этих частей можно составить треугольник.

Решение: Определим пространство элементарных событий . Элементарное событие i характеризуется двумя параметрами x и y , т.к. z=1-(x+y). На них наложено ограничение: x0, y0, x+y1 , тогда можно записать, что ={(x,y);(x+y1)(x0)(y0)}, т.е. пространство элементарных событий есть внутренняя часть треугольника EOD , с катетами, равными единице. Его площадь S_=1/2. Условие, чтобы из 3-х отрезков x,y, 1-(x+y) можно было составить треугольник (событие А), сводится к выполнению следующих условий:

1. сумма двух любых сторон больше третьей;

2. разность двух любых сторон меньше третьей.

Построим такую фигуру  

Событие А – внутренняя часть треугольника АВС. Площадь его S_ABC=1/21/21/2=1/8. Тогда .

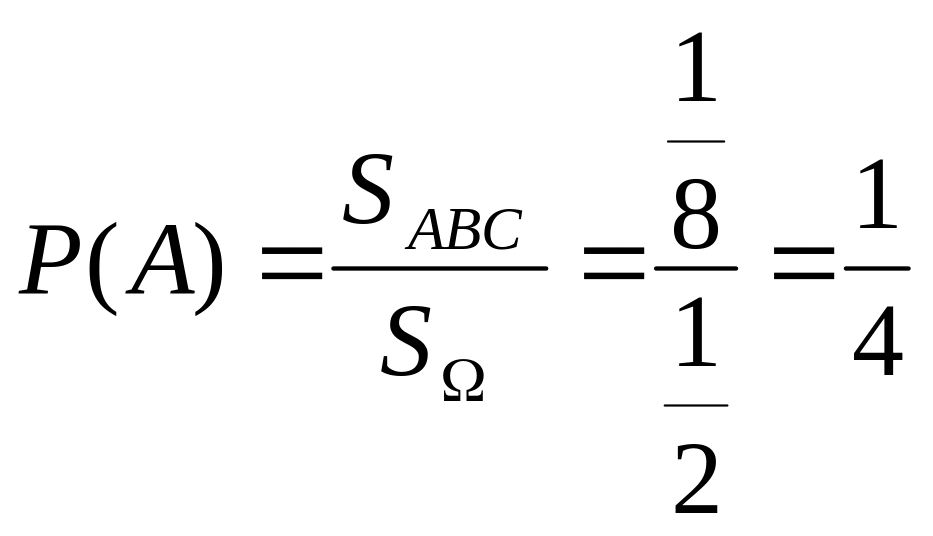Практическое занятие №1

Задача 1. В коробке находится 6 . одинаковых занумерованных кубиков. Наугад по одному извлекаются все кубики. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.

Задача 2. В коробке 5 одинаковых деталей, причем 3 из них окрашены. Наугад извлечены 2 детали. Найти вероятность того, что среди двух извлеченных окажутся:

а) одно окрашенное изделие:

б)два окрашенных изделия;

в)хотя бы одно окрашенное изделие.

Задача 3. На стеллаже в библиотеке в случайном порядке расставлено 15 учебников, причем 5 из них в переплете .Библиотекарь берет наугад 3 учебника . Найти вероятность того, что хотя бы один из них окажется в переплете.

Задача 4. Некто купил карточку Спортлото и отметил в ней 6 из имеющихся 49 номеров, после чего в тираже разыгрываются 6 «выигравших» номеров из 49. Найти вероятности следующих событий:

А₃₌ {верно угаданы 3 номера из 6}

А₄ ={ верно угаданы 4 номера из 6}

А5={ верно угаданы 5 номера из 6}

А6={ верно угаданы 6 номеров из 6}

Задача 5. Десять сообщений случайным образом распределяются по 18 каналам. Найти вероятность события А={на каждый канал придется не более одного сообщения .}

Задача 6. По радиоканалу в течение промежутка времени (0;1) передаются два сигнала длительностью t<1/2; каждый из них с одинаковой возможностью начинается в любой момент интервала (0;1-t). Если сигналы перекроют друг друга хотя бы частично, оба они искажаются и приняты быть не могут. Найти вероятность того, что сигналы будут приняты без искажений.

Задача 7. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложеные ему 3 вопроса.

Задача 8. Вероятность попадания в цель при стрельбе первого и второго орудий равны р1=0.7; р2=0.8. Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одного из орудий.

Задача 9. Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность , равна р=0,4. Произведены три независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную.

Задача 10. В электрическую цепь последовательно включены три элемента, работающие независимо друг от друга. Вероятности отказа 1-го, 2-го, 3-го соответственно равны р1=0.1; р2=0.15; р3=0.2. Найти вероятность того, что тока в цепи не будет.