
Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления
.pdf
9.-
9.1. ¤ ç ¬®¤ «ì®£® ã¯à ¢«¥¨ï
à ªâ¥à ¯¥à¥å®¤ëå ¯à®æ¥áᮢ ¢ á¨á⥬¥ ®¯à¥¤¥«ï¥âáï à á- ¯®«®¦¥¨¥¬ ª®à¥© si ¥¥ å à ªâ¥à¨áâ¨ç¥áª®£® ¬®£®ç«¥ . 1
¥©á⢨⥫ì®, à¥è¥¨¥ y(t) ®¤®à®¤®£® ¤¨ää¥à¥æ¨ «ì®- £® ãà ¢¥¨ï n-£® ¯®à浪 ¨¬¥¥â ¢¨¤ y(t) = Pni=1 Ciyi(t) £¤¥ ¯®áâ®ïë¥ Ci ®¯а¥¤¥«повбп з «мл¬¨ гб«®¢¨п¬¨, б®- бв ¢«пой¨¥ yi(t) ("¬®¤ë") ¨¬¥îâ ¢¨¤ yi(t) = esit - ¯à¨ ¯à®áâëå si ¨«¨ yi(t) = Pi(t)esit { ¯à¨ ªà âëå ª®àïå (§¤¥áì Pi(t) { ¬®- £®з«¥л, бв¥¯¥¨ ª®в®але ®¯а¥¤¥«повбп ªа в®бвмо ª®ап).
®í⮬㠮¡¥á¯¥ç¥¨¥ "å®à®è¨å" ¯¥à¥å®¤ëå ¯à®æ¥áᮢ ¢ á¨- á⥬¥ ¬®¦¥â ¡ëâì ¤®á⨣ãâ® ¥á«¨ å à ªâ¥à¨áâ¨ç¥áª¨© ¬®- £®ç«¥ ¨¬¥¥â § ¤ ë¥ ª®à¨. â® ¥¯®á।á⢥® ¯à¨¢®- ¤¨â ª ãá«®¢¨î ¯®«ãç¥¨ï § ¤ ëå ª®íää¨æ¨¥â®¢ å à ªâ¥- à¨áâ¨ç¥áª®£® ¬®£®ç«¥ § ¬ªã⮩ á¨á⥬ë. ¥£ã«ïâ®àë, ¯®áâà®¥ë¥ ¨áå®¤ï ¨§ 㪠§ ®£® âॡ®¢ ¨ï, §ë¢ îâáï
¬®¤ «ì묨 ॣã«ïâ®à ¬¨.
9.2. ®¤ «ì®¥ ã¯à ¢«¥¨¥ ¯® á®áâ®ï¨î ®¡ê¥ªâ
áᬮâਬ ¢ ç «¥ à¥è¥¨¥ í⮩ § ¤ ç¨ ¯à¨ ¯®«®¬ ¨§¬¥- २¨ ¢¥ªâ®à á®áâ®ï¨ï ®¡ê¥ªâ . «ï ¯à®áâ®âë ¨§«®¦¥- ¨ï ¡ã¤¥¬ â ª¦¥ ¯à¥¤¯®« £ âì, çâ® ã¯à ¢«¥¨¥ ᪠«ï஥,
u(t)2R:
ãáâì ¤¨ ¬¨ª ®¡ê¥ªâ ã¯à ¢«¥¨ï ®¯¨áë¢ ¥âáï ãà ¢¥- ¨¥¬
x(t) = Ax(t) + Bu(t): |
(9.1) |
¥ªâ®à á®áâ®ï¨ï x(t) ®¡ê¥ªâ (9.1) áç¨â ¥¬ ¤®áâã¯ë¬ ¨§¬¥- २î. áᬮâਬ § ª® ã¯à ¢«¥¨ï ¢¨¤
u(t) = ;Kx(t) |
(9.2) |
£¤¥ K { ¯®¤«¥¦ é ï ®¯à¥¤¥«¥¨î n l-¬ âà¨æ ª®íää¨æ¨¥- ⮢ ॣã«ïâ®à (¢ 襬 á«ãç ¥ m = 1): ¬ªãâ ï á¨á⥬ ®¡ê¥ªâ-ॣã«ïâ®à ®¯¨áë¢ ¥âáï ãà ¢¥¨¥¬
x(t) = (A ; BK)x(t): (9.3)
1 ¤¥áì à áᬠâਢ îâáï áâ 樮 àë¥ á¨á⥬ë.
202
â ¢¨âáï § ¤ ç ®¯à¥¤¥«¥¨ï ª®íää¨æ¨¥â®¢ ॣã«ïâ®à (í«¥- ¬¥â®¢ ¬ âà¨æë K) â ª¨å, çâ® å à ªâ¥à¨áâ¨ç¥áª¨© ¬®£®-
I
ç«¥ det(s n ;A+BK) = D(s) = sn +d1sn;1 +: : : +dn;1 +dn ¨¬¥« § ¤ ë¥ ª®íää¨æ¨¥âë di: à¨æ¨¯¨ «ì ï ¢®§¬®¦®áâì à¥- 襨ï í⮩ § ¤ ç¨ ¤«ï ¯®«®áâìî ã¯à ¢«ï¥¬ëå ®¡ê¥ªâ®¢ á«¥¤ã¥â ¨§ 㪠§ ®£® ¢ 7.2. ᢮©á⢠4. 2
áᬮâਬ ¯à®æ¥¤ãàã á¨â¥§ ¡®«¥¥ ¯®¤à®¡®.।¯®«®¦¨¬ ¢ ç «¥, çâ® ãà ¢¥¨ï (9.1) ᮮ⢥âáâ¢ãîâ
ã¯à ¢«ï¥¬®¬ã ª ®¨ç¥áª®¬ã ¯à¥¤áâ ¢«¥¨î, â.¥. ¬ âà¨æë
A B ¨¬¥îâ ¢¨¤ |
|
0 |
|
1 |
|
: : : |
0 |
3 |
|
2 |
0 |
3 |
|
|
||||||||
|
|
2 |
0 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
0 |
|
|
1 |
|
0 |
|
: : : |
0 |
|
|
|
0 |
|
|
|
||||
|
|
A = . |
; |
|
|
; |
|
|
|
|
; |
|
|
5 |
B = . |
5 |
|
(9.4) |
||||
|
|
4 |
; |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|||||
|
|
6 |
0 |
|
|
0 |
|
0 |
|
: : : |
1 |
7 |
|
6 |
0 |
7 |
|
|
||||
|
|
|
an |
|
an;1 |
|
an;2 : : : |
|
a1 |
|
1 |
|
|
|||||||||
det(sIn ;A) = sn +a1sn;1 + +an: ਠ¨á¯®«ì§®¢ ¨¨ ॣã«ï- |
||||||||||||||||||||||
â®à |
(9.2) á ¬ âà¨æ¥© K = [k1 |
k2 : : : kn] ª ª «¥£ª® ã¡¥¤¨âìáï |
||||||||||||||||||||
¥¯®á।á⢥®© ¯®¤áâ ®¢ª®©, ¬ âà¨æ |
A ; BK § ¬ªã⮩ |
|||||||||||||||||||||
á¨á⥬ë (9.3) â ª¦¥ ¨¬¥¥â ¢¨¤ ¬ âà¨æë ஡¥¨ãá |
¨ ¥¥ å - |
|||||||||||||||||||||
à ªâ¥à¨áâ¨ç¥áª¨© ¬®£®ç«¥ det(sIn |
|
|
A + BK) = |
|
|
|
|
|||||||||||||||
= s |
|
+(a1 +kn)s |
|
|
+: : : |
+(an;1 +k2)s+an +k1: |
à¨à ¢¨¢ ï ª®- |
|||||||||||||||
|
n |
|
|
|
n;1 |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
||
íää¨æ¨¥âë §â®£® ¬®£®ç«¥ |
§ ¤ ë¬ § ç¥¨ï¬ di áà §ã |
|||||||||||||||||||||
¯®«ãç ¥¬ ¢ëà ¦¥¨ï ¤«ï ¯ à ¬¥â஢ ॣã«ïâ®à : |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
k1 |
= |
dn |
|
an |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
8 k2 |
= dn;;1 ; an;1 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
> kn;1 |
|
d2 |
|
a2 |
|
|
|
|
|
|
|
|
|
(9.5) |
|||
|
|
|
|
|
= |
; |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
< |
kn |
= |
d1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
; a1: |
|
|
|
|
|
|
|
|
|
|
|||||
ãáâì ⥯¥àì >ãà ¢¥¨ï á®áâ®ï¨ï á¨áâ¥¬ë § ¯¨á ë ¢ |
||||||||||||||||||||||
¯à®¨§¢®«ì®¬, |
:¥ ¢ ª ®¨ç¥áª®¬ ¡ §¨á¥. |
®-¯à¥¦¥¬ã |
||||||||||||||||||||
¯à¥¤¯®« £ ¥¬ ¯®«ãî ã¯à ¢«ï¥¬®áâì ®¡ê¥ªâ |
(9.1). í⮬ |
|||||||||||||||||||||
á«ãç ¥, ᮣ« ᮠ᢮©áâ¢ã 8 |
ã¯à ¢«ï¥¬ëå á¨á⥬ |
(á¬. |
¯. |
|||||||||||||||||||
7.2.), ¨¬¥¥âáï ¬ âà¨æ |
T ¯à¥®¡à §®¢ ¨ï ¯®¤®¡¨ï, ¯à¨¢®¤ï- |
|||||||||||||||||||||
é ï ãà ¢¥¨ï á®áâ®ï¨ï ª 㪠§ ®¬ã ª ®¨ç¥áª®¬ã ¢¨¤ã.3
2 ââ㤠¦¥ á«¥¤ã¥â, çâ® ¥á«¨ ®¡ê¥ªâ ¥ ®¡« ¤ ¥â ¯®«®© ã¯à ¢«ï- ¥¬®áâìî, ¯®«ãç¨âì «î¡ë¥ § ¤ ë¥ ª®íää¨æ¨¥âë ¬®£®ç«¥ D(s) ¢ ¯à¨æ¨¯¥ ¥¢®§¬®¦®.
3 ®à¬ã« ¤«ï ¢ëç¨á«¥¨ï ¬ âà¨æë T ç¥à¥§ ¬ âà¨æë ã¯à ¢«ï¥¬®á⨠¯à¨¢¥¤¥ â ¬ ¦¥.
203
«¥¤®¢ ⥫ì®, ¯®« £ ¥¬, çâ® ¬ âà¨æë |
~ |
|
1 |
~ |
~ |
= T B |
|||
A = T AT |
B |
||||||||
¨¬¥îâ ¢¨¤ (9.4), ¯à¨ç¥¬ det(sIn |
; |
A) |
|
det(sIn |
; |
A): ©¤¥¬ |
|||
~ ~ |
|
|
|
|
|
~ |
|||
¤«ï á¨á⥬ë (A B) ª®íää¨æ¨¥âë ¬®¤ «ì®£® ॣã«ïâ®à K
¯® ä®à¬ã«¥ (9.5). ®á«¥ í⮣® ¢ë¯®«¨¬ ¯¥à¥å®¤ ª ¨á室®-
¬ã ¡ §¨áã. «ï í⮣® § ¬¥â¨¬, çâ® ¯®áª®«ìªã x~(t) = T x(t) â® |
||
~ |
~ |
¥á«¨ |
u(t) = ;Kx~(t) = ;KT x(t) = ;Kx(t) |
||
|
~ |
(9.6) |
|
K = KT: |
|
ª¨¬ ®¡à §®¬, ¤«ï ¯®«®áâìî ã¯à ¢«ï¥¬®© á¨á⥬ë ᮠ᪠- «ïàë¬ ã¯à ¢«¥¨¥¬ ¯®«ãç¥ «£®à¨â¬ à¥è¥¨ï § ¤ ç¨ ¬®- ¤ «ì®£® ã¯à ¢«¥¨ï. â®â «£®à¨â¬ ¢ª«îç ¥â:
{¢ëç¨á«¥¨¥ ª®íää¨æ¨¥â®¢ å à ªâ¥à¨áâ¨ç¥áª®£® ¬®- £®ç«¥ á¨á⥬ë\
{¢ëç¨á«¥¨¥ ¬ âà¨æë ¯à¥®¡à §®¢ ¨ï ª ª ®¨ç¥áª®©
ä®à¬¥ (¥á«¨ ¨áå®¤ë¥ ãà ¢¥¨ï ¨¬¥îâ ¥ª ®¨ç¥áª¨© ¢¨¤)\ { ¢ëç¨á«¥¨¥ ª®íää¨æ¨¥â®¢ ॣã«ïâ®à ¯® ä®à¬ã« ¬
(9.5), (9.6).
¬¥á⥠á ⥬ §¤¥áì ᮤ¥à¦¨âáï ¤®ª § ⥫ìá⢮ ⮣®, çâ® ¤«ï ¯®«®áâìî ã¯à ¢«ï¥¬ëå á¨á⥬ (ᮠ᪠«ïàë¬ ã¯à ¢«¥- ¨¥¬) ᢮©á⢮ 4 ¢ë¢®¤¨âáï ¨§ ᢮©á⢠11. ⬥⨬ â ª¦¥, çâ® ¢ ᨫ㠤㠫ì®á⨠§ ¤ ç ã¯à ¢«¥¨ï ¨ ®æ¥¨¢ ¨ï ¨§«®- ¦¥ë© §¤¥áì ¬¥â®¤ ¯à¨¬¥¨¬ ¨ ¢ à áᬮâ८© ¢ ¯. 8.2. § ¤ ç¥ á¨â¥§ ¡«î¤ ⥫ï á®áâ®ï¨ï. ®«¥¥ ¯®¤à®¡ë¥ ᢥ¤¥¨ï ¯® í⮬㠢®¯à®á㠯ਢ¥¤¥ë ¢ [3].
¯à¥¤¥«¥¨¥ § 票© ¦¥« ¥¬ëå ¯®«îᮢ § ¬ªã⮩ á¨- á⥬ë ï¥âáï á ¬®áâ®ï⥫쮩 § ¤ 祩, à¥è¥¨¥ ª®â®à®© á¢ï§ ® á ¯à¥¤ê塞묨 ª á¨á⥬¥ âॡ®¢ ¨ï¬¨.
§«®¦¥л¥ ¢ бв®пй¥¬ ¯ а £а д¥ а¥§г«мв вл ¥¯®ба¥¤- бв¢¥® ¯¥а¥®бпвбп а¥и¥¨¥ § ¤ з¨ ¬®¤ «м®£® г¯а ¢«¥- ¨п ¤«п ¤¨бªа¥вле б¨бв¥¬. «п бв ж¨® але ¤¨бªа¥вле
á¨á⥬ ¨¬¥¥âáï ¢®§¬®¦®áâì ¯®«ãç¨âì ª®¥ç®¥ ¢à¥¬ï ¯¥à¥- 室®£® ¯à®æ¥áá . â® ®¡¥á¯¥ç¨¢ ¥âáï ¢ë¡®à®¬ å à ªâ¥à¨- áâ¨ç¥áª®£® ¬®£®ç«¥ § ¬ªã⮩ ¤¨áªà¥â®© á¨á⥬ë á ã- «¥¢ë¬¨ ª®íää¨æ¨¥â ¬¨, çâ® ¤ ¥â ¢à¥¬ï ¯¥à¥å®¤®£® ¯à®- æ¥áá , ¥ ¯à¥¢ëè î饥 n è £®¢ ¤¨áªà¥â®áâ¨.
9.3.®¤ «ì®¥ ã¯à ¢«¥¨¥ ¯® ¢ë室㠮¡ê¥ªâ . ¥®à¥- ¬ à §¤¥«¥¨ï
áᬮâਬ ⥯¥àì ¡®«¥¥ å à ªâ¥àãî ¤«ï ¯à ªâ¨ª¨ § ¤ çã, ª®£¤ ¨§¬¥à¥¨î ¤®áâ㯥 ¥ ¢¥ªâ®à á®áâ®ï¨ï x(t) ¢ë室
204
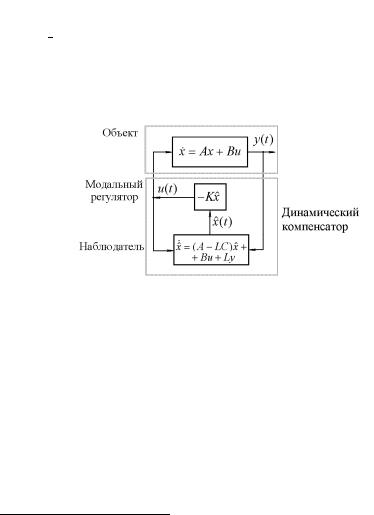
®¡ê¥ªâ y(t): ¡ê¥ªâ ¡ã¤¥¬ áç¨â âì ¥¢ë஦¤¥ë¬ (¯®«®- áâìî ã¯à ¢«ï¥¬ë¬ ¨ ¡«î¤ ¥¬ë¬). í⮬ á«ãç ¥ ¯à¥¤- áâ ¢«ï¥âáï ¥áâ¥áâ¢¥ë¬ ¨á¯®«ì§®¢ âì ¢ § ª®¥ ã¯à ¢«¥¨ï ¥ á ¬¨ ¯¥à¥¬¥ë¥ á®áâ®ï¨ï ®¡ê¥ªâ x(t), ¨å ®æ¥ª¨ x^(t) ¯®«ãç¥ë¥ á ¯®¬®éìî ¡«î¤ ⥫ï (à¨á. 9.1). à ¢¥¨ï § ¬ªã⮩ á¨á⥬ë ⮣¤ ¯à¨¨¬ îâ ¢¨¤
x(t) |
= |
Ax(t) + Bu(t) y(t) = Cx(t) |
x(t0 ) = x0 |
(9.7) |
u(t) |
= |
;Kx^(t) |
|
(9.8) |
x^(t) |
= |
(A ; LC)^x(t) + Bu(t) + Ly(t) |
x^(t0) = x^0: |
(9.9) |
à ¢¥¨ï (9.8), (9.9) ®¯¨áë¢ îâ ॣã«ïâ®à, ¢å®¤®¬ ª®â®à®£® ï¥âáï ¯à®æ¥áá y(t), ¢ë室®¬ { ã¯à ¢«ïî饥 ¢®§¤¥©á⢨¥ u(t): ®â«¨ç¨¥ ®â ॣã«ïâ®à (9.2) ¤ ë© à¥£ã«ïâ®à ï-
¨á. 9.1. ¨á⥬ áâ ¡¨«¨§ 樨 á ¤¨ ¬¨ç¥áª¨¬ ª®¬¯¥á - â®à®¬.
¥âáï ¤¨ ¬¨ç¥áª®© á¨á⥬®©, ¯®à冷ª ª®â®à®© ᮢ¯ ¤ ¥â á ¯®à浪®¬ ãà ¢¥¨© ®¡ê¥ªâ ã¯à ¢«¥¨ï (9.7). ¥£ã«ïâ®àë
â ª®£® ¢¨¤ |
§ë¢ îâáï ¨®£¤ ¤¨ ¬¨ç¥áª¨¬¨ ª®¬¯¥á â®- |
|
à ¬¨ [76]. |
4 |
|
®§¨ª ¥â ¢®¯à®á: ª ª®¢ë ¤¨ ¬¨ç¥áª¨¥ ᢮©á⢠|
á¨á⥬ë |
|
(9.7){(9.9), ª ª ¢«¨ï¥â ᢮©á⢠á¨áâ¥¬ë § ¬¥ |
¢ ¬®¤ «ì- |
|
®¬ ॣã«ïâ®à¥ § 票© á®áâ®ï¨ï ¥£® ®æ¥ª¨? «ï ®â¢¥- â ¥£® ©¤¥¬ å à ªâ¥à¨áâ¨ç¥áª¨© ¬®£®ç«¥ § ¬ªã⮩ á¨á⥬ë.
4 ᯮ«ì§®¢ ¨¥ ¡«î¤ ⥫¥© 㥡¥à£¥à ¯®§¢®«ï¥â 㬥ìè¨âì ¯®- à冷ª ãà ¢¥¨© ª®¬¯¥á â®à ¢¥«¨ç¨ã p = rank C:
205

¯à®áâ¨âì ¢ëç¨á«¥¨¥ ¤ ®£® ¬®£®ç«¥ ¬®¦® ¯à¥- ®¡à §®¢ ¨¥¬ ãà ¢¥¨© á®áâ®ï¨ï. «ï í⮣® ᮢ ¨á¯®«ì- §ã¥¬ ®è¨¡ªã ®æ¥¨¢ ¨ï "(t) = x(t) ; x^(t): ®£¤ ¬®¦¥¬ § ¯¨- á âì x^(t) = x(t); "(t) ¨ га ¢¥¨п (9.7) { (9.9) ¯а¥®¡а §говбп ª ¢¨¤г
|
x(t) = |
Ax(t) + Bu(t) |
x(t0 ) = x0 |
(9.10) |
|||
|
u(t) = |
;Kx(t) + K"(t) |
(9.11) |
||||
|
"(t) = |
(A ; LC)"(t) |
"(t0) = x0 ; x^0: |
(9.12) |
|||
¥à¥å®¤ ®â ãà ¢¥¨© (9.7){(9.9) ª (9.10){(9.12) ᮮ⢥âáâ¢ã¥â |
|||||||
¯à¥®¡à §®¢ ¨î ¢¥ªâ®à |
|
|
|
|
|||
á®áâ®ï¨ï á¨á⥬ë (9.7){(9.9) x~(t) = |
|||||||
|
|
|
|
|
|
|
|
col x(t) x^(t) ª ¢¥ªâ®àã x(t) = col |
x(t) x(t);x^(t) = col |
x(t) "(t) , |
|||||
ª®â®à®¥, ª®¥ç®, ï¥âáï ¥¢ë஦¤¥ë¬. â®á¨â¥«ì® |
|||||||
¢¥ªâ®à |
x(t) ¯®«ã稬 ®¤®à®¤ãî á¨á⥬ã x(t) = Ax(t) £¤¥ |
||||||
¬ âà¨æ |
|
|
|
|
|
|
|
A ¨¬¥¥в б«¥¤гойго ¡«®зго бвагªвгаг: |
|
||||||
|
|
= |
A |
BK |
|
BK |
|
|
A |
|
;0 |
A ; LC : |
|
||
®áª®«ìªã ¬ âà¨æ |
|
|
|
|
|
|
|
A ¨¬¥¥â ¡«®çãî âà¥ã£®«ìãî ä®à¬ã, ¥¥ |
|||||||
å à ªâ¥à¨áâ¨ç¥áª¨© ¬®£®ç«¥ à ¢¥ ¯à®¨§¢¥¤¥¨î å à ªâ- ¥à¨áâ¨ç¥áª¨å ¬®£®ç«¥®¢ ¤¨ £® «ìëå ¡«®ª®¢
det( I ; ) = det( I ; + ) det( I ; + ) s n A s n A BK s n A LC :
¢¨¤ã ⮣® çâ® á¨á⥬ (9.10){(9.12) ¯®«ãç¥ ¥¢ë஦¤¥- ë¬ ¯à¥®¡à §®¢ ¨¥¬ ãà ¢¥¨© (9.7){(9.9), ¨á室 ï § ¬ªã- â ï á¨á⥬ (9.7){(9.9) ¨¬¥¥â â ª®© ¦¥ å à ªâ¥à¨áâ¨ç¥áª¨© ¬®£®ç«¥. «¥¤®¢ ⥫ì®, á¯à ¢¥¤«¨¢ á«¥¤ãîé ï ⥮à¥-
¬ . ¥®à¥¬ à §¤¥«¥¨ï [3, 47]. à ªâ¥à¨áâ¨ç¥áª¨© ¬®£®- ç«¥ § ¬ªã⮩ á¨á⥬ë á ॣã«ïâ®à®¬, ¨á¯®«ì§ãî騬 ®æ¥- ª¨ á®áâ®ï¨ï ®¡ê¥ªâ , ¨ ¡î¤ ⥫¥¬ à ¢¥ ¯à®¨§¢¥¤¥¨î å à ªâ¥à¨áâ¨ç¥áª®£® ¬®£®ç«¥ á¨á⥬ë á "¨¤¥ «ìë¬" ¬®- ¤ «ìë¬ à¥£ã«ïâ®à®¬ (9.2) ¨ å à ªâ¥à¨áâ¨ç¥áª®£® ¬®£®ç«¥-
(8.5) ¡«î¤ ⥫ï (9.9).
®à¨ å à ªâ¥à¨áâ¨ç¥áª®£® ¬®£®ç«¥ á¨á⥬ë (9.7){(9.9) ¯®«ãç îâáï ®¡ê¥¤¨¥¨¥¬ ª®à¥© á¨á⥬ë á ¬®¤ «ìë¬ à¥- £ã«ïâ®à®¬ ¨ ᮡá⢥ëå ç¨á¥« ¡«î¤ ⥫ï á®áâ®ï¨ï. - ª¨¬ ®¡à §®¬, § ¤ ç¨ á¨â¥§ ¬®¤ «ì®£® ॣã«ïâ®à (®¯à¥-
¤¥«¥¨ï ¬ âà¨æë K) ¨ ¡«î¤ ⥫ï (¢ëç¨á«¥¨ï ¬ âà¨æë L) |
|
¬®£ãâ à¥è âìáï ¥§ ¢¨á¨¬®. |
2 |
|
206 |

¬¥â¨¬, çâ® «®£¨ç ï ⥮६ á¯à ¢¥¤«¨¢ ¨ ¯à¨ ¨á- ¯®«ì§®¢ ¨¨ ¡«î¤ ⥫¥© ¯®¨¦¥®£® ¯®à浪 , ®¯¨á ëå ¢ ¯. 8.3. [3].
а ¢¥¨п (9.10){(9.12) ¯®§¢®«пов в ª¦¥ б¤¥« вм ¢л¢®¤, зв® ¯а¨ ®вбгвбв¢¨¨ ¢¥и¨е ¢®§¤¥©бв¢¨© ¯а®ж¥ббл ¢ б¨бв¥- ¬¥ (9.7) { (9.9) ¡г¤гв б¨¬¯в®в¨з¥бª¨ ¯а¨¡«¨¦ вмбп ª ¯а®- ж¥бб ¬ ¢ б¨бв¥¬¥ б ¬®¤ «мл¬ а¥£г«пв®а®¬ ¯® б®бв®п¨о (9.2), ª ª ¥б«¨ ¡л б¨бв¥¬ (9.3) ¡л« ¯®¤¢¥а¦¥ ¤¥©бв¢¨о § вге ой¨е ¢®§¬гй¥¨©. ®«м нв¨е ¢®§¬гй¥¨© ¨£а ¥в б®- бв ¢«пой п K"(t) ¢ ãà ¢¥¨¨ (9.11). ª®à®áâì § âãå ¨ï ®è¨¡ª¨ "(t) ®¯à¥¤¥«ï¥âáï ¯à¨ á¨â¥§¥ ¡«î¤ ⥫ï. à ªâ¨- ç¥áª¨ ४®¬¥¤ã¥âáï ¢ë¡¨à âì ¢à¥¬ï ¯¥à¥å®¤®£® ¯à®æ¥áá ¡«î¤ ⥫ï t ¢ ¥áª®«ìª® à § ¬¥ì訬 âॡ㥬®£® ¢à¥¬¥¨ ¯¥à¥å®¤®£® ¯à®æ¥áá ¢ á¨á⥬¥ á ¬®¤ «ìë¬ à¥£ã«ïâ®à®¬.
¥âà㤮 ã¡¥¤¨âìáï, çâ® ¤«ï SISO-á¨á⥬ (l = m = 1) ãà ¢¥¨ï (9.8), (9.9) ¯à¨¢®¤ïâáï ª ¯¥à¥¤ â®ç®© äãªæ¨¨ ¤¨ ¬¨ç¥áª®£® ॣã«ïâ®à ¢ 楯¨ ®¡à ⮩ á¢ï§¨. 5 ®- í⮬㠨§«®¦¥ë© ¬¥â®¤ á¨â¥§ ¬®¦® à áᬠâਢ âì ª ª ¯®¤å®¤ ª ®¯à¥¤¥«¥¨î ¯ à ¬¥â஢ ª®à४â¨àãî饣® §¢¥ , ®¡¥á¯¥ç¨¢ î饣® § ¤ ®¥ à ᯮ«®¦¥¨¥ ª®à¥© å à ªâ¥à¨-
áâ¨ç¥áª®£® ¬®£®ç«¥ § ¬ªã⮩ á¨á⥬ë. ¥è¥¨¥ í⮩ § ¤ ç¨ ®á®¢¥ ®¯¥à 権 á ¬®£®ç«¥ ¬¨ ¯à¨¢¥¤¥®, - ¯à¨¬¥à, ¢ [76]. «¥¤ã¥â â ª¦¥ ®â¬¥â¨âì, çâ® ¨ ¢ ⮬, ¨ ¢ ¤à㣮¬ á«ãç ¥ âॡã¥âáï ¥¢ë஦¤¥®áâì ®¡ê¥ªâ ã¯à - ¢«¥¨ï. ᫨ ¢ ¯¥à¥¤ â®ç®© äãªæ¨¨ à §®¬ªã⮩ á¨áâ¥- ¬ë ¨¬¥îâáï ᮢ¯ ¤ î騥 㫨 ¨ ¯®«îá , â® ¨å § 票ï
¥¨§¡¥¦® ¡ã¤ãâ ᮤ¥à¦ âìáï á।¨ ª®à¥© å à ªâ¥à¨áâ¨- ç¥áª®£® ¬®£®ç«¥ § ¬ªã⮩ á¨á⥬ë D(s). ¥©á⢨⥫ì- ®, D(s) = A(s) + B(s) £¤¥ A(s) B(s) { § ¬¥ â¥«ì ¨ ç¨- á«¨â¥«ì ¯¥à¥¤ â®ç®© äãªæ¨¨ à §®¬ªã⮩ á¨á⥬ë. ãáâì A(s) = A0(s)R(s) B(s) = B0(s)R(s) â.¥. ¨¬¥îâáï ®¡é¨¥ ã- «¨ ¨ ¯®«îá . ®£¤ D(s) = R(s);A0(s) + B0(s) ¨ á।¨ ª®à- ¥© ¬®£®ç«¥ D(s) ¯à¨ «î¡ëå A0(s) B0(s) ᮤ¥à¦ âáï ª®à¨ R(s): á⮩稢®áâì § ¬ªã⮩ á¨áâ¥¬ë ¬®¦¥â ¡ëâì ®¡¥á¯¥- ç¥ â®«ìª® ¢ ⮬ á«ãç ¥, ª®£¤ ®¨ ¨¬¥îâ ®âà¨æ ⥫ìë¥ ¢¥é¥áâ¢¥ë¥ ç áâ¨, ç⮠ᮮ⢥âáâ¢ã¥â áâ ¡¨«¨§¨à㥬®á⨠¨ ®¡ à㦨¢ ¥¬®á⨠®¡ê¥ªâ ã¯à ¢«¥¨ï.
5 â® ¯®«®¦¥¨¥ ¨««îáâà¨àã¥âáï à áᬮâà¥ë¬ ¢ 9.5.1. ¯à¨¬¥à®¬.
207

9.4. ¥à¬¨ «ì®¥ ã¯à ¢«¥¨¥
ª ®â¬¥ç¥® ¯à¨ ®¯à¥¤¥«¥¨¨ ¯®ïâ¨ï ã¯à ¢«ï¥¬®á⨠(á. 167, ¯. 7.1.), ¯®«®áâìî ã¯à ¢«ï¥¬ãî áâ 樮 àãî á¨á⥬ã
¬®¦® (⥮à¥â¨ç¥áª¨) ¯¥à¥¢¥á⨠¨§ «î¡®£® ç «ì®£® á®- áâ®ï¨ï ¢ «î¡®¥ ¤à㣮¥ § ¯à®¨§¢®«ì® § ¤ ë© ª®¥çë© ¯à®¬¥¦ã⮪ ¢à¥¬¥¨. áᬮâ८¥ ¢ëè¥ ¬®¤ «ì®¥ ã¯à - ¢«¥¨¥ ®¡¥á¯¥ç¨¢ ¥â «¨èì ᨬ¯â®â¨ç¥áªãî áâ ¡¨«¨§ æ¨î á¨á⥬ë, â.¥. { ¯à¨¢¥¤¥¨¥ ¨§ «î¡®£® ¨á室®£® á®áâ®ï¨ï ¢ ã«¥¢®¥ ¯à¨ t ! 1: ® ¬®£¨å ¯à¨«®¦¥¨ïå âॡã¥âáï ¨¬¥-
® à¥è¥¨¥ § ¤ ç¨ ¯®¯ ¤ ¨ï ¢ § ¤ ®¥ á®áâ®ï¨¥ ª § - 祮¬ã ¬®¬¥â㠢६¥¨. ª¨¥ § ¤ ç¨ §ë¢ îâáï § ¤ - ç ¬¨ â¥à¬¨ «ì®£®, ¨«¨ 䨨⮣®, ã¯à ¢«¥¨ï [3, 20]. ¨ ¢®§¨ª îâ, ¯à¨¬¥à, ¯à¨ ¢ë¢¥¤¥¨¨ à ª¥â-®á¨â¥«¥©, á¡«¨- ¦¥¨¨ ¨ ¯®á ¤ª¥ ª®á¬¨ç¥áª¨å ¯¯ à ⮢ [19, 20], ¢ë¯®«¥¨¨ ⨯®¢ëå ¬ ¥¢à®¢ á ¬®«¥â®¢ [23], ¯à¨ ã¯à ¢«¥¨¨ ¬ ¨¯ã«ï-
樮묨 ஡®â ¬¨ ¨ âà ᯮàâ묨 á।á⢠¬¨. 6 ¥è¥- ¨¥ í⮩ § ¤ ç¨ ¤«ï áâ 樮 àëå á¨á⥬ ä ªâ¨ç¥áª¨ ¤ ® ¯à¨ ¤®ª § ⥫ìá⢥ ¯®«®¦¨â¥«ì®© ®¯à¥¤¥«¥®á⨠£à ¬¨ - ã¯à ¢«ï¥¬®á⨠¢ ¯. 7.2. (¯. 10, á. 172). ¬ ¯®ª § ®, çâ® ¤«ï ¯à¨¢¥¤¥¨ï áâ 樮 ண®, ¯®«®áâìî ã¯à ¢«ï¥¬®-
£® ®¡ê¥ªâ |
x(t) = Ax(t) + Bu(t) ¨§ ç «ì®£® á®áâ®ï¨ï x0 |
||||||||||
¢ § ¤ ®¥ á®áâ®ï¨¥ x1 § |
|
㪠§ ë© ¢à¥¬¥®© ¨â¥à¢ « |
|||||||||
= t1 ; t0 |
> 0 ¬®¦® ¨á¯®«ì§®¢ âì |
¯à®£à ¬¬®¥ ã¯à ¢«¥¨¥ |
|||||||||
[3, 30, 83]. |
|
|
|
|
|
|
|
|
|
|
|
|
u(t) = BT eAT (t1;t) |
W |
( );1 |
; |
x1 |
; |
eA x0 |
|
|
(9.13) |
|
£¤¥ £à ¬¨ ã¯à ¢«ï¥¬®á⨠|
|
|
|
|
|
||||||
|
W( ) = Z0 |
eA BBT eAT d : |
|
|
(9.14) |
||||||
ª¨¬ ®¡à §®¬, ©¤¥® ã¯à ¢«¥¨¥ ¥ ¢ ä®à¬¥ ®¡à ⮩ á¢ï§¨ ¯® á®áâ®ï¨î (¨«¨ ¤à㣮© ⥪ã饩 ¨ä®à¬ 樨 ® ¯®-
¢¥¤¥¨¨ ®¡ê¥ªâ ), |
¢ ¢¨¤¥ äãªæ¨¨ ¢à¥¬¥¨, ª®â®à ï ¤®«¦- |
¡ëâì à ááç¨â |
§ à ¥¥, ¨áå®¤ï ¨§ § ¤ ëå § 票© |
x0 x1 . |
|
6 ⮨⠧ ¬¥â¨âì, çâ® ¯®¤ â¥à¬¨®¬ "â¥à¬¨ «ì®¥ ã¯à ¢«¥¨¥" ®¡ëç- ® ¯®¤à §ã¬¥¢ ¥âáï ã¯à ¢«¥¨¥, ¬¨¨¬¨§¨àãî饥 äãªæ¨® «, ª®â®àë© § ¢¨á¨â ®â § 票ï ã¯à ¢«ï¥¬®£® ¯à®æ¥áá ¢ ª®æ¥ à áᬠâਢ ¥¬®£® ¨â¥à¢ « . ®â«¨ç¨¥ ®â â¥à¬¨ "䨨⮥ ã¯à ¢«¥¨¥" §¤¥áì ¥ ®¡ï- § â¥«ì® ¯®¤à §ã¬¥¢ ¥âáï âॡ®¢ ¨¥ ¯à¨¢¥¤¥¨ï á®áâ®ï¨ï á¨áâ¥¬ë ¢ ª®ªà¥âãî â®çªã [2, 3, 23, 93].
208

¯à ¢«¥¨¥ (9.13) ¤«ï à¥è¥¨ï ¤ ®© § ¤ ç¨ ¥ ï¥â- áï ¥¤¨áâ¢¥ë¬ [3]. ® ®¯à¥¤¥«ï¥âáï á â®ç®áâìî ¤® ¥- ª®â®à®© ¤¤¨â¨¢® ¤®¡ ¢«ï¥¬®© äãªæ¨¨ r(t) 㤮¢«¥â¢®àï-
î饩 ãá«®¢¨î t1 eA(t1; )Br( )d = 0: ¥©á⢨⥫ì®, ¤ ë©
tR0
¨â¥£à « (¯® ä®à¬ã«¥ ®è¨ (6.9), á. 130) ¢ëà ¦ ¥â ॠªæ¨î
á¨áâ¥¬ë ¢®§¤¥©á⢨¥ r(t): à¨ à ¢¥á⢥ ¥£® ã«î ॠª- 樨 u(t) ¨ u(t) + r(t) ᮢ¯ ¤ îâ. ª ¯®ª § ® ¢ [3], ã¯à - ¢«¥¨¥ u(t) (9.13) ¨§ ¢á¥å ¢®§¤¥©á⢨©, ¯¥à¥¢®¤ïé¨å x0 ¢ x1, ®¡« ¤ ¥â ¬¨¨¬ «ì®© ®à¬®© (â.¥. ¬¨¨¬¨§¨àã¥â ¨â¥£à «
Rt1 u(t)T u(t)dt).
t0 ¥à¥ç¨á«¨¬ ¥ª®â®àë¥ á¢®©á⢠äãªæ¨¨ W(t0 t1) [3, 47]:
|
W(t0 t1) = tZ0t1 |
(t0 t)B(t)B(t)T (t0 t)T dt: |
|
||||||
â® n n ¬ âà¨ç ï äãªæ¨ï, ª®â®à ï |
|
|
|
||||||
1) |
ᨬ¬¥âà¨ç |
{ W(t0 t1) = W(t0 t1)T \ |
|
|
|||||
2) |
¥®âà¨æ â¥«ì® ®¯à¥¤¥«¥ ¤«ï ¢á¥å t0 t1 t0\ |
|
|||||||
3) 㤮¢«¥â¢®àï¥â «¨¥©®¬ã ¬ âà¨ç®¬ã ¤¨ää¥à¥æ¨ «ì- |
|||||||||
®¬ã ãà ¢¥¨î (ãà ¢¥¨î ï¯ã®¢ ) 7: |
|
|
|||||||
|
_ (t t1 ) = A(t) |
|
(t t1 ) + |
|
(t t1)A(t)T |
|
B(t)B(t)T |
|
|
W |
W |
|
|
W |
|
; |
W(t1 t1) = 0: |
(9.15) |
|
ç áâ®áâ¨, ¤«ï áâ 樮 àëå á¨á⥬ ¯à¨ ! 1 ¬ âà¨æ W( ) ¯à¨¡«¨¦ ¥âáï ª à¥è¥¨î W «£¥¡à ¨ç¥áª®£® ãà ¢¥¨ï
ï¯ã®¢
AW + WAT ; BBT = 0)\
4) 㤮¢«¥â¢®àï¥â äãªæ¨® «ì®¬ã ãà ¢¥¨î
W(t0 t1) = W(t0 t) + (t0 t)W(t t1) (t0 t)T :
ਠ¢ëç¨á«¥¨¨ £à ¬¨ ã¯à ¢«ï¥¬®á⨠(9.14) ¬®¦® â ª¦¥ ãç¥áâì á«¥¤ãî騥 á®®â®è¥¨ï. ¢¥¤¥¬ äãªæ¨î
7 ®«¥¥ ¯®¤à®¡® ¤¨ää¥à¥æ¨ «ì®¥ ¨ |
«£¥¡à ¨ç¥áª®¥ ãà ¢¥¨ï ï- |
¯ã®¢ à áᬠâਢ îâáï ¢ ¯. 11.4.4. á. |
274 ¢ á¢ï§¨ á ¨áá«¥¤®¢ ¨¥¬ |
ãá⮩稢®áâ¨. |
|
209

e
w(t) = AtB: ª ¯®ª § ® ¢ 6.2. (á. 132), ¯à¨ ᪠«ï஬ ¢å®¤- ®¬ ¢®§¤¥©á⢨¨ (m = 1) ¬®¦® âà ªâ®¢ âì w(t), ª ª äãªæ¨î ¢¥á à áᬠâਢ ¥¬®© á¨áâ¥¬ë ¨ 室¨âì, à¥è ï ®¤®à®¤- ®¥ ãà ¢¥¨¥ x(t) = Ax(t) ¯à¨ x(0) = B: ᫨ m > 1, в® ¢ ª з¥бв¢¥ з «мле гб«®¢¨© ¡¥агвбп бв®«¡жл bi ¬ âà¨æë
B= [b1 .b2. : : : .bm] ¨ w(t) 室¨âáï ®¡ê¥¤¨¥¨¥¬ m à¥è¥¨©.⨠᢮©á⢠¬®¦® ¨á¯®«ì§®¢ âì ¯à¨ à¥è¥¨¨ § ¤ ç ä¨-
¨â®£® ¨ â¥à¬¨ «ì®£® ã¯à ¢«¥¨ï.
®«ã祮¥ ¢ëè¥ à¥è¥¨¥ § ¤ ¥â ¯à®£à ¬¬®¥ ã¯à ¢«¥-
¨¥. ।áâ ¢«ï¥â ¨â¥à¥á ¯®«ãç¨âì ã¯à ¢«¥¨¥ ¢ ä®à¬¥ ®¡à ⮩ á¢ï§¨, ª ª íâ® ®¡ëç® ¯à¨ïâ® ¢ á¨á⥬ å ¢â®¬ - â¨ç¥áª®£® ã¯à ¢«¥¨ï. ®ª ¦¥¬, ª ª í⮠ᤥ« âì ¯à¨ à¥è¥-
¨¨ § ¤ ç¨ áâ ¡¨«¨§ 樨, { ª®£¤ |
âॡã¥âáï ¯à¨¢¥á⨠á®áâ®- |
|||||||||||||||||
逸 ®¡ê¥ªâ |
¢ ç «® ª®®à¤¨ â, x1 = 0: |
|
|
|
|
; |
|
|
|
|||||||||
|
¡à ⨬áï ª ä®à¬ã«¥ (9.13). ¡®§ 稢 |
|
|
|
( );1 |
x1 |
|
|||||||||||
|
C = |
W |
; |
|||||||||||||||
|
eA x0 |
|
C |
|
¯®«ã稬 |
|
|
|
|
|
|
|
||||||
; |
|
|
2R T |
AT |
(t1;t) |
|
T ;AT (t;t0) AT |
|
|
|
|
|
|
|
||||
|
|
u(t) = B |
e |
|
C = B |
e |
e |
|
|
= t1 ; t0: |
|
|
||||||
¢¥¤¥¬ ᮯà殮®¥ ãà ¢¥¨¥ 8 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
_(t) = ;AT (t) |
|
(t0) = eA : |
|
|
|
|
(9.16) |
||||||
®£« á® ä®à¬ã«¥ ®è¨, ¥£® à¥è¥¨¥ (t) = e;AT (t;t0) |
(t0) = |
|||||||||||||||||
eAT (t1;t) : à ¢¨¢ ï ¯®«ã祮¥ ¢ëà ¦¥¨¥ ¤«ï (t) á ä®à- ¬ã«®© ¤«ï u(t), ¢¨¤¨¬, çâ® ã¯à ¢«ïî饥 ¢®§¤¥©á⢨¥ ¬®¦®
¢ëà §¨âì ª ª u(t) = BT (t) £¤¥ |
(t) 㤮¢«¥â¢®àï¥â ãà ¢¥- |
|||||||||||||
¨î (9.16), |
(t0) = eAT C: ¡ê¥¤¨ïï ãà ¢¥¨ï ®¡ê¥ªâ , § - |
|||||||||||||
ª® ã¯à ¢«¥¨ï ¨ ᮯà殮®¥ ãà ¢¥¨¥, ¯®«ã稬 á¨á⥬ã |
||||||||||||||
|
x(t) = Ax(t) + Bu(t) x(t0) = x0 |
|
|
|
||||||||||
8 u(t) = BT |
T |
(t) |
|
T |
|
|
(9.17) |
|||||||
> |
_ |
(t) = |
|
|
|
(t) |
A |
|
|
|
|
|||
|
|
A |
|
C: |
|
|||||||||
< |
|
; |
(t0 ) = e |
|
|
|
||||||||
®¤áâ ¢«ïï ¢â®à®¥ ãà ¢¥¨¥ ¢ ¯¥à¢®¥, ¯®«ã稬 á¨á⥬ã |
|
|||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(t) = Ax(t) + BBT (t) x(t0 ) = x0 |
|
|
||||||||||||
( _(t) = |
; |
AT |
|
(t) |
(t0) = eAT C: |
(9.18) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 ¨¥©®¥ ®¤®à®¤®¥ ¤¨ää¥à¥æ¨ «ì®¥ ãà ¢¥¨¥ ¤«ï (t) §ë¢ - ¥âáï ᮯàï¦¥ë¬ ãà ¢¥¨î ®â®á¨â¥«ì® x(t) ¥á«¨ ¤«ï «î¡ëå ç «ì-
ëå ãá«®¢¨© ᪠«ï஥ ¯à®¨§¢¥¤¥¨¥ x(t)T (t) = const: ¥âà㤮 ã¡¥- ¤¨âìáï, çâ® ãà ¢¥¨ï x = Ax ¨ _ = ;AT п¢«повбп б®¯ап¦¥л¬¨ [3].
210

«ï à¥è¥¨ï í⮩ á¨áâ¥¬ë ¬®¦® ¨á¯®«ì§®¢ âì ¯à¥®¡à §®- ¢ ¨¥ ¨ªª ⨠[3, 47, 88]. 㤥¬ ¨áª âì (t) ¢ ¢¨¤¥ (t) = S(t)x(t) £¤¥ S(t) { ¯®¤«¥¦ é ï ®¯à¥¤¥«¥¨î ¬ âà¨æ -äãªæ¨ï.
®¤áâ ®¢ª®© (t) ¢® ¢â®à®¥ ãà ¢¥¨¥ ¨ ¯ã⥬ ¤¨ää¥à¥- |
||||
_ |
= |
|
T |
|
æ¨à®¢ ¨ï ¯®«ãç ¥¬ Sx + Sx |
; |
A Sx: ç¨âë¢ ï ¯¥à¢®¥ |
||
|
|
|
_ |
|
ãà ¢¥¨¥ á¨á⥬ë, ¯®á«¥ ¯®¤áâ ®¢®ª ¯®«ãç ¥¬ |
Sx+ SAx+ |
|||
SBBT Sx = ;AT Sx: â®¡ë ¯®«ã祮¥ à ¢¥á⢮ ¡ë«® ¢ë- |
||||
¯®«¥® ¯à¨ ¢á¥å x, S(t) ¤®«¦ |
㤮¢«¥â¢®àïâì á«¥¤ãî饬ã |
|||
¬ âà¨ç®¬ã ¤¨ää¥à¥æ¨ «ì®¬ã ãà ¢¥¨î: |
|
|||
S_(t) + S(t)A + AT S(t) + S(t)BBT S(t) = 0: |
(9.19) |
|||
â®¡ë ©â¨ ç «ì®¥ § 票¥ S(t0 ), ãç⥬, çâ® à áᬠ- |
||
âਢ ¥âáï § ¤ ç áâ ¡¨«¨§ 樨 ¨ x1 = 0: ®í⮬ã |
|
|
C = ;W( );1eA x0 |
(t0) = ;eAT W( );1eA x0: |
(9.20) |
ª ª ª ¤®«¦® ¢л¯®«пвмбп гб«®¢¨¥ (t0) = S(t0)x(t0) â® ¯®- |
|
«ã稬 S(t0) = ;eAT W( );1 eA . ª¨¬ ®¡à §®¬, ã¯à ¢«¥¨¥, |
|
¯¥à¥¢®¤ï饥 á®áâ®ï¨¥ ®¡ê¥ªâ ¨§ x(t0) = x0 ¢ ã«¥¢®¥ § |
§ - |
¤ ®¥ ¢à¥¬ï > 0, ¢ëà ¦ ¥âáï ¢ ¢¨¤¥ ®¡à ⮩ á¢ï§¨ |
|
u(t) = BT S(t)x(t) |
(9.21) |
£¤¥ S(t) 㤮¢«¥â¢®àï¥â ãà ¢¥¨î (9.19). ®¥ ãà ¢¥¨¥ ï¥âáï ç áâë¬ á«ãç ¥¬ â ª §ë¢ ¥¬®£® ãà ¢¥¨ï ¨ªª - â¨, ª®â®à®¥ ç áâ® ¢áâà¥ç ¥âáï ¯à¨ à¥è¥¨¨ à §«¨çëå ®¯â¨- ¬¨§ 樮ëå § ¤ ç [2, 3, 23, 93, 47]. ਫ®¦¥¨¨ C. á. 423 ¯à¨¢¥¤¥® ®¡à 饨¥ ª MATLAB-¯à®£à ¬¬¥ ¤«ï ¢ëç¨á«¥¨ï ãáâ ®¢¨¢è¥£®áï à¥è¥¨ï í⮣® ãà ¢¥¨ï.
9.5.ਬ¥àë á¨á⥬ ¬®¤ «ì®£® ¨ â¥à¬¨ «ì®£® ã¯à ¢- «¥¨ï
9.5.1.â ¡¨«¨§ æ¨ï 㣫®¢®£® ¤¢¨¦¥¨ï á ª®¬¯¥á 樥© ¢®§¬ã饨©
áᬮâਬ § ¤ çã áâ ¡¨«¨§ 樨 (8.17), á. 194 (á¬. â ª- ¦¥ 1.4.2.). ãáâì âॡã¥âáï ®¡¥á¯¥ç¨âì ¤¢¨¦¥¨¥ ¡¥§ ¢à é¥- ¨ï ¯® ªà¥ã. ய®à樮 «ìë© § ª® áâ ¡¨«¨§ 樨 㣫®¢®©
᪮à®á⨠¨¬¥¥â ¢¨¤
u(t) = ;k!!x(t): |
(9.22) |
211 |
|
