
Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления
.pdf11.-
11.1. ¤ ç¨ ¨ ¬¥â®¤ë ⥮ਨ ¥«¨¥©ëå á¨á⥬
¬¥îâáï ¤¢¥ ®á®¢ë¥ § ¤ ç¨ â¥®à¨¨ ¥«¨¥©ëå á¨á⥬ ã¯à ¢«¥¨ï.
¥à¢ ï ®á®¢ ï § ¤ ç { «¨§. «¨§ á®á⮨⠢ ¨áá«¥- ¤®¢ ¨¨ ¨§¢¥á⮩ ¬ ⥬ â¨ç¥áª®© ¬®¤¥«¨ á¨á⥬ë á 楫ìî ®¯à¥¤¥«¥¨ï ¥¥ ᢮©á⢠¨ ãáâ ®¢«¥¨ï § ¢¨á¨¬®á⨠íâ¨å
᢮©á⢠®â ¯ à ¬¥â஢ á¨á⥬ë. §«¨ç îâ á«¥¤ãî騥 § - ¤ ç¨ «¨§ .
«¨§ ¯à¨ 䨪á¨à®¢ ëå ¯ à ¬¥âà å. ਠ¨áá«¥- ¤®¢ ¨¨ ᢮¡®¤®£® ¤¢¨¦¥¨ï á¨á⥬ë ãáâ ¢«¨¢ ¥âáï à §-
¡¨¥¨¥ ¯à®áâà á⢠á®áâ®ï¨© |
âà ¥ªâ®à¨¨. ëïáïîâ- |
áï áãé¥á⢮¢ ¨¥ ¨ ãá⮩稢®áâì |
ãáâ ®¢¨¢è¨åáï ०¨¬®¢ |
(ª ª®в®ал¬ ®в®бпвбп б®бв®п¨п а ¢®¢¥б¨п, ¯а¥¤¥«мл¥ ж¨- ª«л), ¢лпбповбп ®¡« бв¨ ¯а¨вп¦¥¨п нв¨е а¥¦¨¬®¢. а®- ¨§¢®¤¨вбп ®ж¥ª ª з¥бв¢ ¯¥а¥е®¤ле ¯а®ж¥бб®¢.
믮«ï¥âáï ¨áá«¥¤®¢ ¨¥ å à ªâ¥à ¢ë㦤¥ëå ०¨- ¬®¢ ¯à¨ ¢«¨ï¨¨ á¨á⥬㠢¥è¨å ¢®§¤¥©á⢨©. ¤¥áì âॡã¥âáï ãç¨âë¢ âì ¢¨¤ë ¨ ã஢¨ ¢®§¤¥©á⢨©, ¢®§¨ª -
îé¨å ¢ ¯à®æ¥áᥠíªá¯«ã â 樨 á¨á⥬ë.
«¨§ ¯à¨ à §«¨çëå ¯ à ¬¥âà å. áᬠâਢ ¥âáï ª« áá ¥«¨¥©ëå á¨á⥬ ®¤¨ ª®¢®© áâàãªâãàë, ® ®¡« ¤ - îé¨å à §«¨ç묨 ¯ à ¬¥âà ¬¨ f 1 2 : : : kg: ®çª ¢ ¯à®- áâà á⢥ ¯ à ¬¥â஢ f g ®â¢¥ç ¥â ª®ªà¥â®© á¨á⥬¥ ¨§
¤ ®£® ª« áá . à®áâà á⢮ ¯ à ¬¥â஢ à §¡¨¢ ¥âáï ®¡« á⨠á ⮯®«®£¨ç¥áª¨ íª¢¨¢ «¥â묨 ä §®¢ë¬¨ ¯®àâà¥- â ¬¨. à ¨æë íâ¨å ®¡« á⥩ §ë¢ îâáï ¡¨äãઠ樮묨 ¯®¢¥àå®áâﬨ, ¯®áâ஥¨¥ ª®â®àëå ¨ ¢å®¤¨â ¢® ¢â®àãî § - ¤ çã «¨§ .
â®à ï ®á®¢ ï § ¤ ç { á¨â¥§. ¨в¥§ § ª«оз ¥вбп ¢ ®¯а¥¤¥«¥¨¨ § ª® г¯а ¢«¥¨п, ®¡¥б¯¥з¨¢ ой¥£® ва¥¡г¥- ¬®¥ ( ¯а¨¬¥а, ®¯в¨¬ «м®¥, ¢ ª ª®¬-«¨¡® б¬лб«¥) ª з¥бв¢® а ¡®вл б¨бв¥¬л. ¨в¥§ ¬®¦¥в ¢л¯®«пвмбп ¯а¨ § ¤ ®©
¨«¨ ᢮¡®¤®© áâàãªâãॠॣã«ïâ®à .
¨â¥§ ¯à¨ § ¤ ®© áâàãªâãॠॣã«ïâ®à . ¨¤ § ª®- ã¯à ¢«¥¨ï áç¨â ¥âáï § ¤ ë¬, § ¤ ç á®á⮨⠢ ¯ à -
¬¥âà¨ç¥áª®¬ á¨â¥§¥, â.¥. ¢ ®¯à¥¤¥«¥¨¨ ¯ à ¬¥â஢ ॣã- «ïâ®à , ®¡¥á¯¥ç¨¢ îé¨å ¨«ãç襥 § 票¥ § ¤ ®£® ¯®-
242
ª§ â¥«ï ª ç¥á⢠.
¨¡®«¥¥ ¯à®á⮩ á â®çª¨ §à¥¨ï ¯à¨¢«¥ª ¥¬®© ⥮ਨ ï¥âáï ¯ à ¬¥âà¨ç¥áª¨© á¨â¥§. ¢ë¯®«ï¥âáï ¯®á।-
á⢮¬ «¨§ ¨ ®â¡®à ¢ ਠ⮢ á ¯®¬®éìî ¨§¢¥áâëå ¢ ¬ ⥬ â¨ç¥áª®¬ ¯à®£à ¬¬¨à®¢ ¨¨ «£®à¨â¬®¢ ®¯â¨¬¨§ - 樨. ¤¥áì, ¯à ¢¤ , á«¥¤ã¥â ãç¨âë¢ âì, çâ® ®¡ê¥¬ à ¡®â ¯à¨
«¨§¥ ¬®¦¥â ®ª § âìáï ¥¤®¯ãá⨬® ¡®«ì訬 ¤«ï ¥£® ¬®- £®ªà ⮣® ¢ë¯®«¥¨ï. ஬¥ ⮣®, ¢ ¦® ¯à ¢¨«ì® ¯®- áâநâì äãªæ¨î ª ç¥á⢠á¨á⥬ë, ª®â®à ï ¡ë ¤¥ª¢ â® ®âà ¦ « å à ªâ¥àãî ¤«ï ¯à ªâ¨ª¨ ¬®£®ªà¨â¥à¨ «ì®áâì ¯à¨ ä®à¬ «¨§ 樨 § ¤ ç¨. ®í⮬㠯ਠ¯ à ¬¥âà¨ç¥áª®¬ á¨â¥§¥ ¨¬¥îâ ¡®«ì讥 § 票¥ ¨ ⥮à¥â¨ç¥áª¨¥ ¨áá«¥¤®- ¢ ¨ï.
¨â¥§ ¯à¨ ᢮¡®¤®© áâàãªâãॠॣã«ïâ®à . ¨¤ § - ª® г¯а ¢«¥¨п ¥ § ¤ ¨ ¤®«¦¥ ¡лвм ¯®«гз¥ ¢ а¥§г«м- в в¥ б¨в¥§ . а¨ в ª®© ¯®бв ®¢ª¥ § ¤ з¨ ¨б¯®«м§говбп ¬¥в®¤л ¯¥а¥з¨б«¥ле ¢ ¯. 10.1. ¯а ¢«¥¨© в¥®а¨¨ б¨бв¥¬ (®¯в¨¬ «м®¥, ¤ ¯в¨¢®¥ ¨ нªбва¥¬ «м®¥ г¯а ¢«¥¨¥, ¬¥- в®¤л ¥«¨¥©®© ª®аа¥ªж¨¨, б¨бв¥¬ б ¯¥а¥¬¥®© бвагªвг- а®© ¨ в.¤.). ®¯а®б ®¡ ¨б¯®«м§®¢ ¨¨ в®£®, ¨«¨ ¨®£®, ¬¥в®¤
à¥è ¥âáï ®á®¢¥ ¯à¥¤ê¥ëå ª á¨á⥬¥ âॡ®¢ ¨© ¨ ᢥ¤¥¨© ®¡ ãá«®¢¨ïå ¥¥ à ¡®âë.
¥á¬®âàï â® çâ® á¨â¥§ ¯à¨ ᢮¡®¤®© áâàãªâãॠà¥- £ã«ïâ®à ª ¦¥âáï ¥é¥ ¡®«¥¥ á«®¦ë¬, 祬 ¯ à ¬¥âà¨ç¥áª¨© á¨â¥§, ¤® § ¬¥â¨âì, çâ® ¢ ⥮ਨ ¨§¢¥áâë ¥ª®â®àë¥ ¯®¤- 室ë, ¯à¨ ª®â®àëå áâàãªâãà , ¨®£¤ ¨ ¯ à ¬¥âàë § ª®-
ã¯à ¢«¥¨ï, ¯®«ãç îâáï " ¢â®¬ â¨ç¥áª¨" ¨áå®¤ï ¨§ æ¥- «¨ ã¯à ¢«¥¨ï. â® ®â®á¨âáï, ¯à¨¬¥à, ª à¥è¥¨î àï¤ ®¯â¨¬¨§ 樮ëå § ¤ ç [76, 94], ª á¨â¥§ã ¤ ¯â¨¢ëå § ª®- ®¢ ã¯à ¢«¥¨ï [103, 106] ¨ ॣã«ïâ®à®¢ á ¯¥à¥¬¥®© áâàãªâãன ᪮«ì§ïé¨å ०¨¬ å [102, 191]. ¥ª®â®àë¥ ¨§ ¯¥à¥- ç¨á«¥ëå ¬¥â®¤®¢ à áᬠâਢ îâáï ¨¦¥.
¥®а¨п ¥«¨¥©ле б¨бв¥¬ ¯а®и« ¤«¨в¥«мл© ¯гвм бв - ®¢«¥¨п ¨ ¯а®¤®«¦ ¥в ¨в¥б¨¢® а §¢¨¢ вмбп ¢ бв®пй¥¥ ¢а¥¬п. в в¥®а¨п ¯®бв®п® ®¡®£ й ¥вбп а¥§г«мв в ¬¨, ¢ ¥¥ а ¬ª е ¯®п¢«повбп ®¢л¥ ¯а ¢«¥¨п.
¥â®¤ë ⥮ਨ ¥«¨¥©ëå á¨á⥬ ¬®¦® à §¡¨âì - «¨â¨ç¥áª¨¥ ¨ ç¨á«¥ë¥. «¨â¨ç¥áª¨¥ ¬¥â®¤ë ¢ á¢®î ®ç¥-
à¥¤ì ¬®¦® à §¤¥«¨âì â®çë¥ ¨ ¯à¨¡«¨¦¥ë¥. ।¨ ç¨- á«¥ëå ¬¥â®¤®¢ ¨áá«¥¤®¢ ¨ï ®á®¢ãî à®«ì ¨£à îâ ᥩç á
243
¬ è¨ë¥ ¬¥â®¤ë, á¢ï§ ë¥ á ¨§ã票¥¬ ᢮©á⢠¥«¨¥©- ëå á¨á⥬ , å®âï 室ï⠯ਬ¥¥¨¥ ¨ £à ä¨ç¥áª¨¥, ¨«¨ £à ä®- «¨â¨ç¥áª¨¥, ¬¥â®¤ë.
®çë¥ ¬¥â®¤ë ¢ ®â«¨ç¨¥ ®â ¯à¨¡«¨¦¥ëå ¨¬¥îâ áâண®¥ ⥮à¥â¨ç¥áª®¥ ®¡®á®¢ ¨¥, ïá ®¡« áâì ¨å ¯à¨¬¥¥¨ï, ¯®- «ãç¥ë¥ á ¯®¬®éìî íâ¨å ¬¥â®¤®¢ १ã«ìâ âë ¤ îâ â®çë¥ (á ãç¥â®¬ ¢ë¯®«¥ëå ¯à¥¤¢ à¨â¥«ìëå ¤®¯ã饨©) ᢥ¤¥- ¨ï ® á¨á⥬¥. ¥¤®áâ ⪠¬ íâ¨å ¬¥â®¤®¢ ®â®á¨âáï ®¡ëç® áà ¢¨â¥«ì® 㧪 ï ®¡« áâì ¯à¨¬¥¥¨ï { ¥ª®â®àë¥ ãá«®¦- ¥¨ï ¬®¤¥«¨ á¨áâ¥¬ë ¬®£ã⠯ਢ¥á⨠ª ¥¢®§¬®¦®á⨠©- ⨠¯®¤å®¤ï騩 â®çë© ¬¥â®¤. à㣨¬ ¨å ¥¤®áâ ⪮¬ ¬®- £ãâ ®ª § âìáï ¢ë᮪¨¥ âॡ®¢ ¨ï ª ⥮à¥â¨ç¥áª®© ¯®¤£®â®¢- ª¥ ¨áá«¥¤®¢ ⥫ï. ਡ«¨¦¥ë¥ ¬¥â®¤ë ¬¥¥¥ § ¢¨áïâ ®â á«®¦®á⨠à áᬠâਢ ¥¬®© § ¤ ç¨ ¨, ªà®¬¥ ⮣®, ®à¨¥â¨- ஢ ë ¨á¯®«ì§®¢ ¨¥ ¨¦¥¥àëå ¬¥â®¤¨ª ¯à®¥ªâ¨à®¢ - ¨ï.
«¨â¨ç¥áª¨¥ ¬¥â®¤ë ¢ ¯à¨æ¨¯¥ ¯®§¢®«ïîâ ¯®«ãç¨âì १ã«ìâ â ¢ ®¡é¥¬ ¢¨¤¥ { ¢ ä®à¬¥ á®®â®è¥¨©, á¢ï§ë¢ î- é¨å ¯ à ¬¥âàë á¨á⥬ë á ¥¥ å à ªâ¥à¨á⨪ ¬¨. â® ã¯à®- é ¥â ¯à®æ¥¤ãàã ¯ à ¬¥âà¨ç¥áª®£® á¨â¥§ . ® «¨â¨ç¥-
᪨¥ ¬¥â®¤ë ®¡« ¤ îâ ¬¥ì襩 㨢¥àá «ì®áâìî, 祬 ç¨á- «¥ë¥. â® á¢ï§ ® á ¨§¢¥á⮩ á«®¦®áâìî «¨â¨ç¥- ᪮£® ¨áá«¥¤®¢ ¨ï ¥«¨¥©ëå á¨á⥬. à㣮© ¯à®¡«¥¬®©, ¢®§¨ª î饩 ¯à¨ ¨á¯®«ì§®¢ ¨¨ «¨â¨ç¥áª¨å ¬¥â®¤®¢, ¬®- ¦¥â áâ âì á«®¦®áâì ¯®«ãç¥ëå ¢ëà ¦¥¨© ¤«ï ¯®á«¥¤ãî- 饣® ¨á¯®«ì§®¢ ¨ï. í⮬ á«ãç ¥ ¬®¦¥â ®ª § âìáï, çâ® ¥-
¯®á।á⢥®¥ ¯à¨¬¥¥¨¥ ç¨á«¥ëå ¬¥â®¤®¢ ¯®§¢®«ï¥â á ¬¥ì訬¨ ¯à¥¤¢ à¨â¥«ì묨 § âà â ¬¨ ¨ ¤®¯ã饨ﬨ ¯®- «ãç¨âì âà¥¡ã¥¬ë© à¥§ã«ìâ â.
¨¦¥ ¡ã¤ãâ à áᬮâà¥ë ¥ª®â®àë¥ ¨§¢¥áâë¥ ¬¥â®¤ë ¨á- á«¥¤®¢ ¨ï ¥«¨¥©ëå á¨á⥬.
11.2. ¥â®¤ë ä §®¢®£® ¯à®áâà áâ¢
¥в®¤л д §®¢®£® ¯а®бва бв¢ ®в®бпвбп ª ¨¡®«¥¥ а ¨¬ в®зл¬ «¨в¨з¥бª¨¬ ¬¥в®¤ ¬ в¥®а¨¨ ¥«¨¥©ле б¨бв¥¬.
¨¬ ®â®á¨âáï ¬¥â®¤ ä §®¢®© ¯«®áª®á⨠( ¥®â¥, 1885) ¨
¬¥â®¤ â®ç¥çëå ®â®¡à ¦¥¨© ( ã ª à¥, ¨àª£®ä) [79].
244

11.2.1. ¥â®¤ ä §®¢®© ¯«®áª®áâ¨
¥â®¤ ä §®¢®© ¯«®áª®á⨠¨á¯®«ì§ã¥âáï ¤«ï ¨áá«¥¤®¢ ¨ï ¢- â®®¬ëå á¨á⥬ ¢â®à®£® ¯®à浪 ¨ § ª«îç ¥âáï ¢ ¯®áâ஥-
¨¨ д §®¢ле ¯®ава¥в®¢. «п нв®£® ¨§ га ¢¥¨© б®бв®п¨п ¨бª«оз ¥вбп ¢а¥¬п ¨ ®¯а¥¤¥«повбп га ¢¥¨п д §®¢ле ªа¨- ¢ле. а¨ ¨б¯®«м§®¢ ¨¨ нв®£® ¬¥в®¤ ж¥«¥б®®¡а §® ¯а¨¢¥- ¤¥¨¥ га ¢¥¨© б¨бв¥¬л ª ª ®¨з¥бª®© д®а¬¥.
¤ ç áâ |
®¢¨âáï ¤®áâ â®ç® ¯à®á⮩, ¥á«¨ à áᬠâਢ ¥- |
âáï á¨á⥬ |
á ªãá®ç®-«¨¥©®© å à ªâ¥à¨á⨪®©. ®£¤ ¢ |
à §ëå ®¡« áâïå ¯à®áâà á⢠á®áâ®ï¨© á¨á⥬ ®¯¨áë¢ ¥- âáï «¨¥©ë¬¨ ãà ¢¥¨ï¬¨, ¢ ᮮ⢥âá⢨¨ á ª®â®à묨 áâà®- ïâáï ä §®¢ë¥ âà ¥ªâ®à¨¨. «¥¥ ¢ë¯®«ï¥âáï "á訢 ¨¥" âà ¥ªâ®à¨© ¯® «¨¨ï¬ ¯¥à¥ª«î票ï, ®¯à¥¤¥«ï¥¬ë¬ ¢¨¤®¬ ¥«¨¥©®© § ¢¨á¨¬®áâ¨. â® ¯®§¢®«ï¥â ¯®áâநâì ä §®¢ë© ¯®àâà¥â ¨áá«¥¤ã¥¬®© ¥«¨¥©®© á¨á⥬ë.1 «¥¥, ¯®áª®«ìªã
á®áâ®ï¨ï £à ¨æ å ¨â¥à¢ «®¢ ®¯à¥¤¥«¥ë, ¬®¦® ¯®«ã- ç¨âì ¨ ¢¨¤ ¯¥à¥å®¤ëå ¯à®æ¥áᮢ ¢ á¨á⥬¥ (¬¥â®¤ ¯à¨¯ á®-
¢ë¢ ¨ï).
®âï íâ®â ¬¥â®¤ ¨¬¥¥â ®£à ¨ç¥®¥ ¯à¨¬¥¥¨¥, ® ®áâ ¥- âáï 㤮¡ë¬ á।á⢮¬ ¨áá«¥¤®¢ ¨ï ¥«¨¥©ëå á¨á⥬ ¥- ¢ë᮪®£® ¯®à浪 á "¯à®áâ묨" ¥«¨¥©ë¬¨ å à ªâ¥à¨áâ¨- ª ¬¨.
11.2.2. ¥â®¤ â®ç¥çëå ®â®¡à ¦¥¨©
¥â®¤ â®ç¥çëå ®â®¡à ¦¥¨©, ¨«¨ ®â®¡à ¦¥¨© ã ª à¥, á®á⮨⠢ ¯®áâ஥¨¨ ¥ª®â®à®© ᥪã饩 ¯®¢¥àå®á⨠L ¨ âà - ¥ªâ®à¨©, ¢ë¯ãé¥ëå ¨§ L. ¤® ¨§ ®á®¢ëå ¯à¨¬¥¥¨© ¬¥â®¤ { «¨§ ãá⮩稢®á⨠¨ ®¯à¥¤¥«¥¨¥ ¯ à ¬¥â஢ (ç - áâ®âë ¨ ¬¯«¨âã¤ë) ¯à¥¤¥«ìëå 横«®¢ ¯à¨ n = 2: §«®¦¨¬ ¢ªà âæ¥ ®á®¢ë¥ ¯®«®¦¥¨ï ¤ ®£® ¬¥â®¤ , á«¥¤ãï [79].
|
ãáâì G |
¥áâì ¥ª®â®àë© ¯à¥¤¥«ìë© æ¨ª«. 롥६ ªà¨- |
||||||||||||||
¢ãî L |
{ ᥪãéãî, ¡¥§ ª á ¨ï ¯¥à¥á¥ª îéãî G. ãáâì â®çª |
|||||||||||||||
x0 |
2 G |
x0 |
2 L |
{ â®çª |
|
¯¥à¥á¥ç¥¨ï ªà¨¢ëå |
G |
¨ |
L |
. 롥६ |
||||||
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|||||
¡«¨§ªãî ª ¥© â®çªã x |
|
2 L. ãáâì ᮮ⢥âáâ¢ãîé ï x âà - |
||||||||||||||
¥ªâ®à¨ï ¯¥à¥á¥ª ¥â ¢ á«¥¤ãî騩 à § ªà¨¢ãî |
|
|
¢ ¥ª®â®à®© |
|||||||||||||
â®çª¥ x |
|
2 L. ¢¨á¨¬®áâì x |
|
= |
(x ) ¥áâì â®ç¥ç®¥ ®â®¡à - |
|||||||||||
|
|
|
00 |
|
|
|
|
|
00 |
|
0 |
|
L |
|
|
|
1 ¤¥áì ¨á¯®«ì§ã¥âáï ᢮©á⢮, ᮣ« á® ª®â®à®¬ã ª®¥çë¥ § 票ï á®áâ®ï¨ï á¨áâ¥¬ë ¥ª®â®à®¬ ¨â¥à¢ «¥ ¬®£ã⠨ᯮ«ì§®¢ âìáï ¢ ª - ç¥á⢥ ç «ìëå ¤«ï á«¥¤ãî饣® ¨â¥à¢ « , á¬. 1.1.
245
¦¥¨¥, ¯¥à¥¢®¤ï饥 ¨á室ãî â®çªã ¯à®áâà á⢠á®áâ®ï- ¨© ¢ ¤àã£ãî ¢ ᮮ⢥âá⢨¨ á ãà ¢¥¨ï¬¨ á¨á⥬ë. ®çª
x0, 室ïé ïáï âà ¥ªâ®à¨¨ ¯à¥¤¥«ì®£® 横« , ï¥âáï |
|||
¥¯®¤¢¨¦®© â®çª®© ®â®¡à ¦¥¨ï ( ), â.¥. |
¢ë¯®«¥® à - |
||
¢¥á⢮ x0 = (x0). |
|
|
|
¢¥¤¥¬ (x) { à ááâ®ï¨¥ ¢¤®«ì «¨¨¨ |
L |
®â ç «ì®© â®ç- |
|
|
|
|
|
ª¨ O í⮩ ªà¨¢®© ¤® â®çª¨ x: ¡®§ 稬 g = |
(x0) h = (x00): |
||
ᯮ«ì§ãï â®ç¥ç®¥ ®â®¡à ¦¥¨¥, ¯®«ãç ¥¬ äãªæ¨î ¯®á«¥-
¤®¢ ¨ï h = '(g): 祢¨¤®, çâ® ¥á«¨ g0 |
|
= (x0 ) â® ¥¯®¤¢¨¦- |
|
ï â®çª , ¯à¨ ¤«¥¦ é ï ¯à¥¤¥«ì®¬ã 横«ã, 室¨âáï ¨§ |
|
à¥è¥¨ï ãà ¢¥¨ï |
|
g0 = '(g0): |
(11.1) |
à ä¨ç¥áª¨ à¥è¥¨¥ í⮣® ãà ¢¥¨ï ¬®¦® ¯à¥¤áâ ¢¨âì ª ª ®âë᪠¨¥ â®ç¥ª ¯¥à¥á¥ç¥¨ï ¡¨áᥪâà¨áë ª®®à¤¨ ⮩ ¯«®áª®á⨠(g h) á äãªæ¨¥© ¯®á«¥¤®¢ ¨ï h = '(g): §ãç¥- ¨¥ ¯®¢¥¤¥¨ï äãªæ¨¨ ¯®á«¥¤®¢ ¨ï ¢ â®çª å ¯¥à¥á¥ç¥¨ï
¤ ¥â ¢®§¬®¦®áâì ®¯à¥¤¥«¨âì ãá⮩稢®áâì ᮮ⢥âáâ¢ãî- |
|||
饣® ¯à¥¤¥«ì®£® 横« . |
᫨ 0 < d'(g) |
|
< 1 â® |
|
dg |
|
g=g0 |
¨¬¥¥âáï ãáâ®©ç¨¢ë© ¯à¥¤¥«ìë© æ¨ª« ( ¢â®ª®«¥¡ ¨ï)\ ¥á«¨ |
|||
d'(g) |
|
|
|
dg g=g0 > 1 â® ¯à¥¤¥«ìë© æ¨ª« ¥ãá⮩稢 (¡®«¥¥ ¯®¤à®¡- |
|||
ë¥ á¢¥¤¥¨ï ¯à¨¢¥¤¥ë ¢ [79]). ¨¡®«ìèãî á«®¦®áâì ¢ ¨á- ¯®«ì§®¢ ¨¨ ¬¥â®¤ â®ç¥çëå ®â®¡à ¦¥¨© ¢ë§ë¢ ¥â ®¯à¥- ¤¥«¥¨¥ äãªæ¨¨ ¯®á«¥¤®¢ ¨ï.
ਬ¥à ¨á¯®«ì§®¢ ¨ï ¬¥â®¤ â®ç¥çëå ®â®¡à ¦¥¨© ¤«ï ¨áá«¥¤®¢ ¨ï £¥¥à â®à ª®«¥¡ ¨© à áᬮâॠ¢ ¯. 11.3.4.
á.256.
¯®á«¥¤¥¥ ¢à¥¬ï ¯®ï¢¨«¨áì ¯ã¡«¨ª 樨, ¢ ª®â®àëå ¬¥- ⮤ â®ç¥çëå ®â®¡à ¦¥¨© ¨á¯®«ì§ã¥âáï ¤«ï ¨áá«¥¤®¢ ¨ï å ®â¨ç¥áª¨å ¯à®æ¥áᮢ, á¬. [72] ¨ ¯. 13.3.
11.2.3.á«®¢¨ï áãé¥á⢮¢ ¨ï ¯à¥¤¥«ìëå 横«®¢ ¤«ï á¨- á⥬ ¢â®à®£® ¯®à浪
а ¬ª е ¬¥в®¤ д §®¢®© ¯«®бª®бв¨ ¯®«гз¥л б«¥¤гой¨¥ а¥- §г«мв вл, ¨¬¥ой¨¥ ¢ ¦®¥ § з¥¨¥ ¯а¨ ¨бб«¥¤®¢ ¨¨ «¨- з¨п ¯а¥¤¥«мле ж¨ª«®¢ г б¨бв¥¬ ¢в®а®£® ¯®ап¤ª [94]. ¨¬, ¢ ¯¥а¢го ®з¥а¥¤м, ®в®бпвбп в¥®а¥¬л г ª а¥{ ¥¤¨ªб® .
246

¥®à¥¬ |
1 ( . ã ª à¥). «ï ¯à®¨§¢®«ì®© § ¬ªã⮩ |
|||||||||||
®¡« áâ¨ ä §®¢®© ¯«®áª®á⨠2 à §¨æ |
¬¥¦¤ã ç¨á«®¬ 室ï- |
|||||||||||
é¨åáï ¢ãâਠ¥¥ ®á®¡ëå â®ç¥ª ⨯ |
"㧥«", "æ¥âà", "䮪ãá" |
|||||||||||
N ¨ ®á®¡ëå â®ç¥ª ⨯ |
"ᥤ«®" S à ¢ 1, â.¥. ¨¤¥ªá ã - |
|||||||||||
|
; S = 1: |
|
|
|
|
|
|
|
|
|
|
|
ª ॠIP = N |
|
|
|
|
|
|
|
|
|
|
|
|
¥®à¥¬ |
2 ( ¯¥à¢ ï ⥮६ |
|
. ¥¤¨ªá® ). ᫨ ¤«ï |
|||||||||
á¨áâ¥¬ë ¢â®à®£® ¯®à浪 |
|
|
|
|
|
|
|
|
|
|
||
|
|
x1 |
(t) = f1 |
(x1 x2) |
|
|
|
|
||||
|
x2 |
(t) = f2 |
(x1 x2) |
|
|
|
|
|||||
äãªæ¨¨ f1 |
(x1 x2 ) f2(x1 x2) ¨¬¥îâ ç áâë¥ ¯à®¨§¢®¤ë¥ ¯® |
|||||||||||
x1 x2 â® ¯à¥¤¥«ìë© æ¨ª« ¥ áãé¥áâ¢ã¥â ¢ ⮩ ®¡« á⨠P |
||||||||||||
ä §®¢®© ¯«®áª®áâ¨, £¤¥ |
@f1(x1 |
x2) |
+ |
@f2(x1 |
x2 ) ¥ à ¢ |
ã«î |
||||||
¨«¨ ¥ ¨§¬¥ï¥â § ª . |
|
|
@x1 |
|
|
@x2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
¥®à¥¬ |
3 ( ¢â®à ï ⥮६ |
¥¤¨ªá® ). ᫨ âà ¥ªâ®- |
||||||||||
à¨ï ¢â®®¬®© á¨áâ¥¬ë ¢â®à®£® ¯®à浪 |
室¨âáï ¢ãâਠ|
|
||||||||||
®£à ¨ç¥®© ®¡« á⨠P ¨ ¯à¨ í⮬ ¥ áâ६¨âáï ª ¯®«®¦¥- |
|
|||||||||||
¨î à ¢®¢¥á¨ï, â® íâ |
âà ¥ªâ®à¨ï ï¥âáï «¨¡® ãá⮩ç¨- |
|
||||||||||
¢ë¬ ¯à¥¤¥«ìë¬ æ¨ª«®¬, «¨¡® áâ६¨âáï ª ¥¬ã. |
|
|
|
|||||||||
¥®à¥¬ |
4 ( . ã ª à¥). |
¬ªãâ ï âà ¥ªâ®à¨ï G 3 |
¢- |
|||||||||
â®®¬®© á¨áâ¥¬ë ¢â®à®£® ¯®à浪 |
ï¥âáï ãáâ®©ç¨¢ë¬ |
|
||||||||||
¯à¥¤¥«ìë¬ æ¨ª«®¬, ¥á«¨ |
R |
@f1 |
(x1 x2 ) + |
@f2(x1 x2) |
|
dt < 0: |
||||||
|
|
|
|
G |
|
@x1 |
@x2 |
|
|
|
||
11.3.¥â®¤ £ ମ¨ç¥áª®© «¨¥ ਧ 樨 (£ ମ¨ç¥- ᪮£® ¡ « á )
¥â®¤ £ ମ¨ç¥áª®© «¨¥ ਧ 樨 (¯® ¤à㣮© â¥à¬¨®«®£¨¨ { £ ମ¨ç¥áª®£® ¡ « á ) ®â®á¨âáï ª ¯à¨¡«¨¦¥ë¬ «¨- â¨ç¥áª¨¬ ¬¥â®¤ ¬ ¨áá«¥¤®¢ ¨ï ¥«¨¥©ëå á¨á⥬. â®â ¬¥â®¤ ¨¬¥¥â ¤ ¢îî ¨áâ®à¨î. ¢®á室¨â ª à ¡®â ¬. . àë«®¢ ¨ . . ®£®«î¡®¢ (1934), . . ®«ì¤ä à¡
(1957), . ®ç¥¡ãࣥà (1950), . . ®¯®¢ (1960). ¥â®¤ è¨- ப® ¨á¯®«ì§ã¥âáï ¢ ¨¦¥¥à®© ¯à ªâ¨ª¥, ¯à¨¬¥ï¥âáï ¢ â¥- ®à¥â¨ç¥áª¨å ¨áá«¥¤®¢ ¨ïå ¨ ¯à®¤®«¦ ¥â à §¢¨¢ âìáï.
¥â®¤ £ ମ¨ç¥áª®© «¨¥ ਧ 樨 ¯à¥¤ § ç¥ ¯à¥¦¤¥ ¢á¥£® ¤«ï ¨áá«¥¤®¢ ¨ï ¯¥à¨®¤¨ç¥áª¨å ( ¢â®ª®«¥¡ ⥫ìëå)
2 ⮬ ç¨á«¥ ¨ ¯à¥¤¥«ì®£® 横« .
3 ®ç¥¥ { ®à¡¨â «ì® ᨬ¯â®â¨ç¥áª¨ ãá⮩稢ë¬, á¬. á. 264.
247

¯à®æ¥áᮢ ¢ ¥«¨¥©ëå á¨á⥬ å, ®¤ ª® ¨§¢¥áâ® ¯à¨¬¥¥-
¨¥ ¬¥â®¤ |
¨ ¤«ï ¨áá«¥¤®¢ ¨ï |
ª®«¥¡ ⥫ìëå ¯¥à¥å®¤ëå |
¯à®æ¥áᮢ, |
â ª¦¥ ¤«ï à¥è¥¨ï |
¡®«¥¥ è¨à®ª®£® ªà㣠§ ¤ ç |
[15, 76, 84, 94, 113].
11.3.1. á®¢ë¥ ¯®«®¦¥¨ï. " ¢®©á⢮ 䨫ìâà "
áᬮâਬ § ¬ªãâãî ¥«¨¥©ãî á¨á⥬ã á ®¤¨¬ ¥«¨- ¥©ë¬ ¡«®ª®¬, ãà ¢¥¨ï ª®â®à®© ¨¬¥îâ ¢¨¤ (á¬. â ª¦¥ ¯.
10.7)
x(t) |
= |
Ax(t) + B |
; ; |
(t) (t) = Cx(t) |
(t) |
= |
'( (t)): |
|
¤¥áì x(t) |
2 Rn { ¢¥ªâ®à á®áâ®ï¨ï «¨¥©®© ç á⨠á¨á⥬ë\ |
(t) 2 R { ¢ë室 «¨¥©®© ç á⨠á¨á⥬ë\ (t) 2 R { ¯®áâã- |
|
¯ î騩 |
¢å®¤ «¨¥©®© ç á⨠¢ë室 ¥«¨¥©®© ç á⨠ᮠ|
áâ â¨ç¥áª®© å à ªâ¥à¨á⨪®© '( ). 4 ¥à¢®¥ ¨§ ãà ¢¥¨© |
|||||
(11.2) § ¤ ¥â «¨¥©ãî ç áâì |
|
|
|
||
á¨á⥬ë. ¬ã ᮮ⢥âáâ¢ã¥â |
|||||
¯¥à¥¤ â®ç ï äãªæ¨ï |
|
|
|
|
|
|
|
|
B(s) |
|
|
W« (s) = C sIn ; A);1B = A(s) |
(11.2) |
||||
®â ¢å®¤ (; ) ª ¢ë室ã ;: |
|
|
|
5 |
|
ᯮ«ì§ãï ®¯¥à â®àãî ä®à¬ã § ¯¨á¨ |
|
á ®¯¥à â®à®¬ |
|||
|
d |
|
|
|
|
¤¨ää¥à¥æ¨à®¢ ¨ï p = |
|
ãà ¢¥¨ï (11.2) ¬®¦¥¬ ¯¥à¥¯¨- |
|||
dt |
|||||
á âì ¢ ¢¨¤¥ |
|
|
|
|
|
A(p) (t) = |
;B(p) (t) |
|
(11.3) |
||
(t) = |
'( (t)) |
|
|
||
¢ ª®â®à®¬ ª®íää¨æ¨¥âë ®¯¥à â®àëå ¬®£®ç«¥®¢ A(p) B(p)
ᮢ¯ ¤ îâ á ª®íää¨æ¨¥â ¬¨ ¬®£®ç«¥®¢ A(s) B(s) ¯¥à¥¤ - â®ç®© äãªæ¨¨ (11.2).
ãáâì ¢ á¨á⥬¥ (11.3) ¨¬¥¥â ¬¥áâ® ¯¥à¨®¤¨ç¥áª¨© ¯à®- æ¥áá á ¥ª®â®à®© ç áâ®â®© (¨ ¯¥à¨®¤®¬ T = 2 = ). á
4 ª "¬¨ãá" ¯à¨ ¢å®¤®¬ ¯à®æ¥áᥠ¢ ¯¥à¢®¬ ãà ¢¥¨¨ ¢§ïâ ¤«ï ⮣®, ç⮡ë á®åà ¨âì âà ¤¨æ¨®®¥ ¤«ï ª« áá¨ç¥áª®© ⥮ਨ «¨¥©ëå á¨á⥬ ¯à ¢¨«® § ª®¢ ¢ £« ¢®© ®¡à ⮩ á¢ï§¨ á¨á⥬ë.
5 ¬¥â¨¬, çâ® â ª ï ä®à¬ § ¯¨á¨ ï¥âáï, ¯® áãé¥áâ¢ã, ª®¬¯ ªâ- ®© § ¯¨áìî ¤¨ää¥à¥æ¨ «ì®£® ãà ¢¥¨ï n-£® ¯®à浪 , ¯®«ã祮£® ¨§ (11.2).
248

¯à¥¦¤¥ ¢á¥£® ¡ã¤¥â ¨â¥à¥á®¢ âì ®¯à¥¤¥«¥¨¥ å à ªâ¥à¨á⨪
í⮣® ¯à®æ¥áá |
( ¬¯«¨âã¤ë ¨ ç áâ®âë), |
â ª¦¥ «¨§ ¥£® |
ãá⮩稢®áâ¨. |
â ª, ¯®« £ ¥¬, çâ® (t) |
(t + T ): ®£¤ ¨ |
(t) (t + T ): |
|
|
ᮢ®¥ ¤®¯ã饨¥, ¯à¨ï⮥ ¢ ¬¥â®¤¥ £ ମ¨ç¥áª®© |
||
«¨¥ ਧ 樨, â ª §ë¢ ¥¬ ï £¨¯®â¥§ |
(᢮©á⢮) 䨫ìâà , |
|
á®á⮨⠢ ⮬, çâ® ¤«ï ¬¯«¨â㤮-ç áâ®â®© å à ªâ¥à¨áâ¨-
|
|
ª¨ «¨¥©®© ç á⨠á¨á⥬ë H(!) = jW« (|!)j ¢ë¯®«¥® ¥à - |
|
¢¥á⢮ |
|
H ( ) H(k ) k = 2 3 4 : : : |
(11.4) |
â.¥. ª®íää¨æ¨¥â ¯¥à¥¤ ç¨ «¨¥©®© ç á⨠á¨á⥬ë |
®á®¢- |
®© ç áâ®â¥ § ç¨â¥«ì® ¯à¥¢®á室¨â ª®íää¨æ¨¥â ¯¥à¥¤ ç¨ ¤«ï ¢ëáè¨å ç áâ®â. 6
«ì¥©è¨© ¯« ¤¥©á⢨© á®á⮨⠢ á«¥¤ãî饬. ।- ¯®« £ ï £¨¯®â¥§ã 䨫ìâà ¢ë¯®«¥®©, § ¬¥â¨¬, çâ® ¬®¦® ¯à¥¥¡à¥çì á®áâ ¢«ïî騬¨ ¯à®æ¥áá ¢ë室¥ «¨¥©®© ç - áâ¨ á ¢ëá訬¨ ç áâ®â ¬¨ 2 3 : : : (¢¢¨¤ã ¬ «®á⨠¤«ï ¨å ª®íää¨æ¨¥â ¯¥à¥¤ ç¨) ¨ áç¨â âì, çâ® ¢ë室¥ «¨¥©®©
з бв¨ ¨¬¥¥вбп £ ମ¨з¥бª¨© б¨£ « б з бв®в®© . ¢л- 室¥ ¥«¨¥©®© з бв¨ б¨бв¥¬л ª®¥з® ¯®п¢пвбп б®бв ¢«по- й¨¥ б ¢лби¨¬¨ з бв®в ¬¨ (¥ ¢лбª §л¢ ¥вбп ¯а¥¤¯®«®¦¥¨© ® д¨«мвагой¨е б¢®©бв¢ е ¥«¨¥©®£® §¢¥ ). ® ¨§-§ в®£® зв® ¢лби¨¥ £ ମ¨ª¨ ¥ ¢л§л¢ ов бгй¥бв¢¥®© а¥ ªж¨¨ ¢л室¥ «¨¥©®© з бв¨ б¨бв¥¬л, ¬®¦® ¥ гз¨вл¢ вм ¨е
¢«¨п¨п ¤¨ ¬¨ªг § ¬ªгв®© б¨бв¥¬л. «¥¤®¢ в¥«м®, ¯а¨ ¨бб«¥¤®¢ ¨¨ § ¬ªгв®© б¨бв¥¬л (11.2) ¬®¦® ¯а¨¡«¨- ¦¥® бз¨в вм, зв® ª ª ¢е®¤, в ª ¨ ¢л室 ¥«¨¥©®£® §¢¥ п¢«повбп £ ମ¨з¥бª¨¬¨ ª®«¥¡ ¨п¬¨, 7 ¡« £®¤ àï 祬㠨 ¢ë¯®«ï¥âáï (£ ମ¨ç¥áª ï) «¨¥ ਧ æ¨ï ¥«¨¥©®áâ¨.
6 ª ¢¨¤®, ¤ ®¥ ᢮©á⢮ ä®à¬ã«¨àã¥âáï ¢ ¥ç¥âª¨å â¥à¬¨ å.஬¥ ⮣®, ¤«ï ¥£® ¯à®¢¥àª¨ á«¥¤ã¥â § âì ®á®¢ãî ç áâ®âã, ª®â®à ï ¥é¥ ¯®¤«¥¦¨â ®¯à¥¤¥«¥¨î. ®í⮬㠬®¦® áç¨â âì ᢮©á⢮ 䨫ìâà a priori ¢ë¯®«¥ë¬, § ⥬ ¯à®¢®¤¨âì «¨§ H(!) ¤«ï ©¤¥®© ®á®¢- ®© ç áâ®âë, á¬. â ª¦¥ [113].
7 ®§¬®¦®, зв® нв¨ ª®«¥¡ ¨п ¥б¨¬¬¥ва¨зл¥ ¨ ᮤ¥а¦ в ¯®бв®п- го б®бв ¢«пойго. ¥в®¤ £ ମ¨з¥бª®© «¨¥ а¨§ ж¨¨ ¯а¨¬¥п¥вбп ¨ ¤«п ¨бб«¥¤®¢ ¨п в ª¨е ¯а®ж¥бб®¢ [15, 76, 94, 113], ®¤ ª® ¤«п ¯а®бв®вл ¨§«®¦¥¨п ¬л §¤¥бм бз¨в ¥¬ ª®«¥¡ ¨п б¨¬¬¥ва¨зл¬¨.
249
11.3.2. ®íää¨æ¨¥âë £ ମ¨ç¥áª®© «¨¥ ਧ 樨
®£« ᮠᤥ« ®¬ã ¢ëè¥ ¯à¥¤¯®«®¦¥¨î, ª ª ¢å®¤¥, â ª ¨ ¢ë室¥ ¥«¨¥©®£® §¢¥ ¨¬¥îâáï £ ମ¨ç¥áª¨¥ ¯à®-
æ¥ááë ®¤¨ ª®¢®© ç áâ®âë : ª®© ¢ë¢®¤ ¬®¦® ᤥ« âì ®â- ®á¨â¥«ì® ᢮©á⢠í⮣® §¢¥ ?
áᬮâਬ á«¥¤ãî騥 ¯à¨¬¥àë.
ਬ¥à 1. ãáâì (t) = A sin t { £ ମ¨ç¥áª¨© ¯à®æ¥áá á ¬¯«¨â㤮© A = 0 ¨ ç áâ®â®© : ।¯®«®¦¨¬, çâ® ¢ë-
6
室®© ¯à®æ¥áá ¤ ®£® §¢¥ ¥áâì ⮦¥ £ ମ¨ª ç áâ®âë
, ᮢ¯ ¤ îé ï ¯® ä §¥ á® ¢å®¤ë¬ ¯à®æ¥áᮬ, ® ¨¬¥îé ï
¬¯«¨âã¤ã A1 â.¥. (t) = A1 sin t: |
||||
§ ¯¥à¢®£® ¢ëà ¦¥¨ï 室¨¬, çâ® sin t = |
(t) |
: ®¤áâ - |
||
|
||||
|
|
|
A |
|
¢«ïï íâ® ¢ëà ¦¥¨¥ ¢ ä®à¬ã«ã ¤«ï (t) ¯®«ã稬 |
||||
A1 |
A1 |
|
|
|
(t) = A (t) = q (t) |
£¤¥ q = A |
{ ¥ª®â®àë© ª®íää¨æ¨¥â. |
||
ª¨¬ ®¡à §®¬, ¯à¨ ᤥ« ®¬ ¯à¥¤¯®«®¦¥¨¨, à áᬠ- |
||||
âਢ ¥¬®¥ §¢¥® ¢¥¤¥â á¥¡ï ª ª |
«¨¥©®¥ ¡¥§ë¥à樮®¥ |
|||
§¢¥® (t) = q (t) á ª®íää¨æ¨¥â®¬ ¯¥à¥¤ ç¨ q: ª®¥ §¢¥®
(s) = q:
¬ ¥ ç ¨ ¥ . ®«ãç¥ë© १ã«ìâ â ¥ ¯®§¢®«ï¥â ᤥ-
«âì ¢ë¢®¤ ® ⮬, çâ® ¤ ®¥ §¢¥® ï¥âáï «¨¥©ë¬ ¨ ¡¥-
§ë¥à樮ë¬, â ª ª ª ¥ à áᬮâà¥ë ¯à®¨§¢®«ìë¥ ¢å®¤ë¥ ¯à®æ¥ááë. ⢥ত ¥âáï «¨èì, çâ® ¯® ®â®è¥¨î ª® ¢å®¤®- ¬ã £ ମ¨ç¥áª®¬ã ¢å®¤®¬ã ¯à®æ¥ááã á ¤ 묨 ç áâ®â®© ¨ ¬¯«¨â㤮© à áᬠâਢ ¥¬®¥ §¢¥® ¢¥¤¥â á¥¡ï ª ª «¨¥©- ®¥.
ë᪠§ ®¬ã ¤®¯ãé¥¨î ® ¢®§¬®¦®á⨠ãç¨âë¢ âì ⮫ì-
ª® ®á®¢ãî £ ମ¨ªã ¥ ¯à®â¨¢®à¥ç¨â § ¢¨á¨¬®áâì ®â®- è¥¨ï ¬¯«¨â㤠A1 ¨ A ¨, á«¥¤®¢ ⥫ì®, â ª¦¥ ª®íää¨- 樥⠯¥à¥¤ ç¨ q ®â ¬¯«¨âã¤ë ¨«¨ ®â ç áâ®âë ¢å®¤®£® ¯à®æ¥áá : q = q(A) q = q(A ): ®®â¢¥âá⢥® ¯®«ã稬 W(s A) = q(A) W (s A ) = q(A ) { ¯¥à¥¤ â®çë¥ äãªæ¨¨ £ ମ¨ç¥áª¨ «¨¥ ਧ®¢ ëå §¢¥ì¥¢ § ¢¨áïâ ®â A (¨«¨ ®â
A ¨ ), ª ª ®â ¯ à ¬¥âà . â ª®© § ¢¨á¨¬®á⨠¨ ¯à®ï¢«ï¥â- áï ¯à¨æ¨¯¨ «ì®¥ ®â«¨ç¨¥ å à ªâ¥à¨á⨪ «¨¥©ëå §¢¥ì¥¢ ®â ¥«¨¥©ëå.
ਬ¥à 2. ãáâì ⥯¥àì ¯à¨ â®¬ ¦¥ ¢å®¤®¬ ¯à®æ¥áá¥(t) = A sin t ¢ë室®© ¯à®æ¥áá ¨¬¥¥â ä §®¢ë© ᤢ¨£, â.¥.(t) = A1 sin t+B1 cos t: ¨ää¥à¥æ¨àãï ¢ëà ¦¥¨ï ¤«ï (t)
250
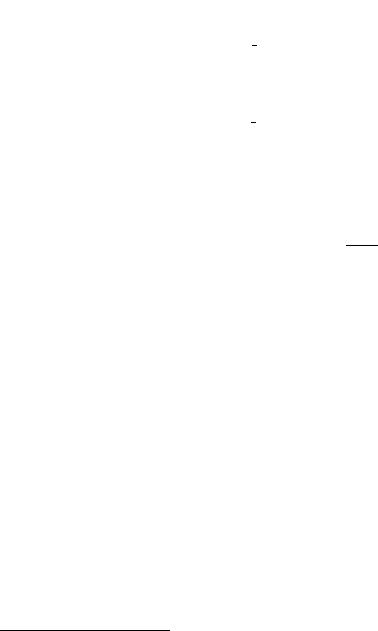
¯® t ¨ ¯à¥¤¯®« £ ï, çâ® A = 0 |
= 0 ¯®«ã稬 ¢ëà ¦¥¨¥ ¤«ï |
|||||||||
|
|
6 |
1 |
6 |
|
|
|
|
|
|
cos t ç¥à¥§ (t) : cos t = |
|
(t): |
®¤áâ ¢«ïï ¥£® ¢ ä®à¬ã«ã |
|||||||
A |
||||||||||
¤«ï |
(t) ¨ á ãç¥â®¬ ©¤¥®£® ¢ ¯à¨¬¥à¥ 1 ¢ëà ¦¥¨ï ¤«ï |
|||||||||
|
|
A1 |
|
B1 |
1 |
|
|
A1 |
||
sin t ¯®«ã稬 (t) = A (t) + A |
|
|
(t): ¡®§ 稢 |
q = |
A |
|||||
|
|
|||||||||
|
B1 |
¯¥à¥¯¨è¥¬ ¢ëà ¦¥¨¥ ¤«ï (t) ¢ ¢¨¤¥ |
|
|
||||||
q0 = |
A |
|
|
|||||||
(t) = q (t) + q0 (t):
ª ¨ ¢ ¯à¥¤ë¤ã饬 ¯à¨¬¥à¥, ª®íää¨æ¨¥âë q, q0, §ë¢ - ¥¬ë¥ ª®íää¨æ¨¥â ¬¨ £ ମ¨ç¥áª®© «¨¥ ਧ 樨 ¥«¨¥©- ëå §¢¥ì¥¢, ¬®£ãâ § ¢¨á¥âì ®â ¬¯«¨âã¤ë ¨ ç áâ®âë ¢å®¤®-
£® ¯à®æ¥áá : q = q(A) q0 = q0(A) ¨«¨ q = q(A ) q0 = q0(A ):
®«ã祮¬ã ¢ëà ¦¥¨î ᮮ⢥âáâ¢ã¥â ¯¥à¥¤ â®ç ï äãª- q0 (A)
s: 8
áᬮâਬ ⥯¥àì "â¥å¨ªã" ¢ëç¨á«¥¨ï ª®íää¨æ¨¥â®¢
£à¬®¨ç¥áª®© «¨¥ ਧ 樨. ãáâì ¯®-¯à¥¦¥¬ãæ¨ï §¢¥ )= ( )+ä®àá¨àãî饣® ⨯ : W (
(t) = A sin t: ।áâ ¢¨¬ ¯¥à¨®¤¨ç¥áª¨© ¢ë室®© ¯à®æ¥áá(t) ¢ ¢¨¤¥ àï¤ ãàì¥ [15, 66, 76, 94]:
(t) '( (t)) '(Asin t) = |
A0 |
+ A1 sin t + B1 cos t + |
+ |
A2 |
sin(2 t) + B2 cos(2 t) + : |
®£« á® ¯à¨ï⮩ £¨¯®â¥§¥, ®£à ¨ç¨¬áï á« £ ¥¬ë¬¨ á ç - áâ®â®© ¥ ¢ëè¥ ç áâ®âë ®á®¢®© £ ମ¨ª¨, â.¥. ¯à¨¬¥¬
(t) A0 + A1 sin t + B1 cos t £¤¥ ª®íää¨æ¨¥âë à §«®¦¥¨ïãàì¥ ®¯а¥¤¥«повбп ¢ла ¦¥¨п¬¨ [66]
|
|
1 |
|
2 |
|
|
|
|
A0 |
= |
Z0 |
'(Asin |
)d |
|
|
||
|
|
|||||||
2 |
|
|||||||
A1 |
= |
1 Z0 |
2 |
'(A sin |
) sin |
d |
(11.5) |
|
B1 |
= |
1 Z0 |
2 |
'(A sin |
) cos |
d |
|
|
®¤áâ ®¢ª®© ¯®«ãç¥ëå § 票© ¢ ¢ëà ¦¥¨ï ¤«ï q(A)
8 «ï §¢¥ì¥¢ á ¯ áᨢ®© £¨áâ¥à¥§¨á®© å à ªâ¥à¨á⨪®© q0(A) < 0 ¯®í⮬㠫¨¥ ਧ®¢ ®¥ §¢¥®, ª ª ¯à ¢¨«®, ¥¬¨¨¬ «ì®-ä §®¢®¥.
251
