
Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления
.pdf
ª¨¬ ®¡à §®¬, § ¬ëª ¨¥ ã¯à ¢«ï¥¬®© á¨áâ¥¬ë ®¡à â- ®© á¢ï§ìî ¯® á®áâ®ï¨î u(t) = Kx(t) ¯à¨ «î¡®© ¬ âà¨æ¥ K ¯à¨¢®¤¨â â ª¦¥ ª ã¯à ¢«ï¥¬®© á¨á⥬¥.
9. ᫨ ¯ à |
(A B) ã¯à ¢«ï¥¬ ¨ si { ¯à®¨§¢®«ì®¥ ᮡ- |
||
á⢥®¥ ç¨á«® ¬ âà¨æë A, â® ¤¥ä¥ªâ d ¬ âà¨æë siIn |
; |
A ¥ |
|
¯à¥¢®á室¨â à £ |
¬ âà¨æë B [30]. 6 |
|
|
ç áâ®áâ¨, ¥á«¨ m = 1 (¨«¨ ¥á«¨ ¯à¨ m > 1 rankB = 1) в® ¤®«¦® ¢л¯®«пвмбп d = 1 â.¥. ¨§ ã¯à ¢«ï¥¬®á⨠¯ àë (A B) á«¥¤ã¥â, çâ® ª ¦¤®¬ã ᮡá⢥®¬ã § 票î si ®â- ¢¥ç ¥â «¨èì ®¤ ª«¥âª ª ®¨ç¥áª®© ¦®à¤ ®¢®© ä®à¬ë
¬âà¨æë A:
10.«ï «î¡ëå t1 > t0 ¬ âà¨æ
t1
|
|
T |
T |
|
|
|
|
||
W(t0 t1) = tZ0 |
eA BB |
|
eA d |
(7.3) |
§ë¢ ¥¬ ï £à ¬¨ ®¬ ã¯à ¢«ï¥¬®áâ¨, ¯®«®¦¨â¥«ì® ®¯à¥- ¤¥«¥ .
«ï ¤®ª § ⥫ìá⢠¯à¥¤¯®«®¦¨¬, ç⮠㪠§ ®¥ ãá«®¢¨¥ ¢ë¯®«¥® [30], W(t0 t1)=W(t0 t1 )T > 0 ¤«ï ¢á¥å t1 >t0: ¯à ¢- «¥¨¥, u[t0 t1] ¯¥à¥¢®¤ï饥 á¨á⥬㠨§ á®áâ®ï¨ï x(t0) = x0 ¢
á®áâ®ï¨¥ x(t1) = x1 ¡ã¤¥¬ ¨áª âì ¢ ¢¨¤¥ u(t) = BT eAT (t1;t)C £¤¥ C { ¥ª®â®àë© ¯®áâ®ïë© n-¬¥àë© ¢¥ªâ®à. ®£« á®
ä®à¬ã«¥ ®è¨ (6.9, á. 130) ¨ ¢ ᨫã áâ 樮 à®á⨠á¨á⥬ë |
||||||||||||||||||
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
eA(t1;t0) |
= |
|
tt01 eA(t1; )BBT eAT (t0; )d ¨«¨ x2 |
; |
eA = |
W |
( ) |
||||||||||
£¤¥; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
= t1 ; t0 |
> 0 |
W( ) = W(0 ) = Z0 |
eA BB |
|
eA d : |
|
|||||||||||
® ãá«®¢¨î |
W |
( ) > 0 á«¥¤®¢ ⥫ì®, det |
W |
( ) = 0 ¨ ¯®í⮬ã |
||||||||||||||
C = |
W( ) |
;1 |
|
A |
x0 |
|
|
|
|
6 |
|
|
|
|
|
|||
|
x1 |
; e |
: ª®ç ⥫ì®, ¯®«ãç ¥¬ ¢ëà ¦¥¨¥ |
|||||||||||||||
¤«ï ã¯à ¢«¥;¨ï |
|
|
;x1 ; eA x0 |
: |
|
|
|
|
|
|||||||||
|
|
u(t) = BT eAT (t1;t)W( );1 |
|
|
|
(7.4) |
||||||||||||
©¤¥®¥ â ª¨¬ ®¡à §®¬ ã¯à ¢«¥¨¥ à¥è ¥â § ¤ çã ¯¥à¥- |
||||||||||||||||||
¢®¤ |
¯®«®áâìî ã¯à ¢«ï¥¬®© á¨áâ¥¬ë ¨§ «î¡®£® ç «ì®£® |
|||||||||||||||||
6 ¥ä¥ªâ®¬ ¬ âà¨æë §ë¢ ¥âáï à §®áâì ¬¥¦¤ã ¥¥ ¯®à浪®¬ ¨ à - £®¬. ¥ä¥ªâ ¬ âà¨æë siIn ; A à ¢¥ ç¨á«ã ¦®à¤ ®¢ëå ª«¥â®ª ¢ ª ®¨- ç¥áª®© ä®à¬¥ ¬ âà¨æë A ®â¢¥ç îé¨å ᮡá⢥®¬ã § 票î si.
172

á®áâ®ï¨ï x(t0) = x0 ¢ «î¡®¥ § ¤ ®¥ x(t1) = x1 § 㪠§ - ë© ¯®«®¦¨â¥«ìë© ¯à®¬¥¦ã⮪ ¢à¥¬¥¨ = t1 ; t0 ¤«ï ¢á¥å t1 > t0\ á«¥¤®¢ ⥫ì®, ¯ à (A B) ã¯à ¢«ï¥¬ .
¬¥â¨¬, çâ® §¤¥áì ¯à¨¢¥¤¥® ⮫쪮 ¤®ª § ⥫ìá⢮ ¤®- áâ â®ç®á⨠¯®«®¦¨â¥«ì®© ®¯à¥¤¥«¥®á⨠W(t0 t1) ¤«ï ¯®«- ®© ã¯à ¢«ï¥¬®á⨠á¨á⥬ë. ¥®¡å®¤¨¬®áâì í⮣® ãá«®¢¨ï, àï¤ã á ¤à㣨¬¨ ªà¨â¥à¨ï¬¨ ¤®ª §ë¢ ¥âáï [3, 30, 83].
®á«¥¤¨© ªà¨â¥à¨© ¬®¦® ¨á¯®«ì§®¢ âì ¨ ¤«ï ¨áá«¥¤®- ¢ ¨ï ã¯à ¢«ï¥¬®á⨠¥áâ 樮 àëå á¨á⥬ ¢ á«¥¤ãî饩
ä®à¬ã«¨à®¢ª¥.
¨¥© ï á¨á⥬ (á ¯¥à¥¬¥ë¬¨ ¯ à ¬¥âà ¬¨)
x(t) = A(t)x(t)+B(t)u(t) ¯®«®áâìî ã¯à ¢«ï¥¬ ⮣¤ , ¨ ⮫ì-
ª® ⮣¤ , ª®£¤ |
¤«ï ¢á¥å t0 áãé¥áâ¢ã¥â t1 (t0 < t1 < 1) |
çâ® |
|||||||||||||||
¬ âà¨æ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Zt0 |
|
|
|
T |
|
T |
|
|
|
|
|
|
W(t0 t1) = |
(t1 )B( )B |
|
( ) |
|
(t1 )d |
|
|
|
|||||||||
¥¢ë஦¤¥ ï (§¤¥áì (t ) { ¯¥à¥å®¤ ï ¬ âà¨æ |
á¨á⥬ë, |
||||||||||||||||
á¬. ¯. 6.3). |
|
|
|
|
|
|
|
2 R m = 1) ¨¬¥îâáï â ª¦¥ á«¥- |
|||||||||
«ï SIMO-á¨á⥬ (u(t) |
|||||||||||||||||
¤ãî騥 ªà¨â¥à¨¨ ¯®«®© ã¯à ¢«ï¥¬®áâ¨. |
|
~ |
~ |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
11. «ï «î¡®© ¤à㣮© ã¯à ¢«ï¥¬®© ¯ àë (A B) â ª®©, |
|||||||||||||||||
çâ® det(sIn |
|
A) |
|
det(sIn |
|
~ |
|
|
|
|
|
|
|
|
|
||
; |
|
; |
A) áãé¥áâ¢ã¥â ¥¤¨á⢥ ï ¬ - |
||||||||||||||
|
|
|
|
|
|
|
|
|
~ |
|
|
;1 |
|
|
|||
âà¨æ ¯à¥®¡à §®¢ ¨ï T det T =0 â ª ï, çâ® |
A=T AT |
|
|
||||||||||||||
~ |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
B = T B: |
|
|
|
|
|
|
|
|
|
~ |
|
|
|
~ |
|
|
|
âà¨æ |
|
|
|
|
|
|
|
|
|
;1 |
|
|
|
;1 |
|||
T ®¯à¥¤¥«ï¥âáï ä®à¬ã«®© T = QãQã |
£¤¥ Qã Qã |
||||||||||||||||
|
|
|
|
|
|
|
|
~ |
|
~ |
|
|
|
|
|
|
|
{ ¬ âà¨æë ã¯à ¢«ï¥¬®á⨠á¨á⥬ (A B) ¨ (A B) ᮮ⢥â-
á⢥®. ç áâ®áâ¨, «î¡ãî ¯®«®áâìî ã¯à ¢«ï¥¬ãî áâ - 樮 àãî SIMO-á¨á⥬ã (m = 1) ¬®¦® ¯à¥®¡à §®¢ âì ª ª -
®¨ç¥áª®¬ã ã¯à ¢«ï¥¬®¬ã ¯à¥¤áâ ¢«¥¨î (á¬. ¯. 3.2.2.), ¢ ª®â®à®¬ ¬ âà¨æ ~ { ᮯ஢®¦¤ îé ï ¤«ï ᢮¥£® å à ªâ¥-
A
à¨áâ¨ç¥áª®£® ¬®£®ç«¥ (¬ âà¨æ ஡¥¨ãá )
|
|
2 |
0 |
|
1 |
|
0 |
: : : |
0 |
3 |
|
|||
~ |
= |
0 |
|
0 |
|
1 |
: : : |
0 |
|
|||||
A |
. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
4 |
0 |
;~ |
0 |
|
0 |
: : : |
1 |
5 |
|
|||
|
|
; |
|
n ; |
n;1 |
|
; |
|
|
|||||
|
|
6 |
|
an |
an;1 |
|
an;2 |
: : : |
|
a1 |
7 |
|
||
|
det(sIn ; A) = s |
+ a1s |
|
+ + an |
||||||||||
|
|
|
|
|
|
|
173 |
|
|
|
|
|
|
|
n 1-¬ âà¨æ |
~ |
|
|
T |
7 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
B = [0 0 : : : 0 1] . |
|
|
|
|
|
|
|
|
|||||||
|
12. ᥣ¤ |
©¤¥âáï â ª ï (1 n)-¬ âà¨æ |
C çâ® ¯¥à¥¤ - |
|
|||||||||||
â®ç ï äãªæ¨ï |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
B(s) |
|
|
|
|
|
|
|
|
W(s) = C(sI ; A);1B = |
|
|
(7.5) |
|||||||||
|
|
|
det(sI ; A) |
||||||||||||
{ ¥á®ªà ⨬ ï ¤à®¡ì (â.¥. ¥ ¨¬¥¥â ®¡é¨å ã«¥© ¨ ¯®«îᮢ |
|
||||||||||||||
¨ á⥯¥ì § ¬¥ ⥫ï W(s) à ¢ n). |
|
|
|
|
|
|
|||||||||
|
13. «ï «î¡®£® § ¤ ®£® ¬®£®ç«¥ B(s) á⥯¥¨ n ; |
|
|||||||||||||
1 ¢á¥£¤ |
©¤¥âáï â ª ï (1 n)-¬ âà¨æ |
C çâ® ¯¥à¥¤ â®ç ï |
|
||||||||||||
äãªæ¨ï ¨¬¥¥â ¢¨¤ (7.5). |
|
|
|
|
|
|
|
|
|
||||||
¢®©á⢮ 12 ¤ ¥â 㤮¡®¥ ¤®áâ â®ç®¥ ãá«®¢¨¥ ¯®«®© ã¯- |
|
|
|||||||||||||
à ¢«ï¥¬®á⨠á¨á⥬ ᮠ᪠«ïàë¬ ¢å®¤®¬: ¥á«¨ W(s) ¥á®- |
|
||||||||||||||
ªà ⨬ , â® á¨á⥬ |
¯®«®áâìî ã¯à ¢«ï¥¬ . ¡à ⮥ ¬®- |
|
|
||||||||||||
¦¥â ®ª § âìáï ¥¢¥àë¬. |
|
|
|
|
|
|
|
|
|
||||||
7.3. |
à¨â¥à¨¨ ¡«î¤ ¥¬®áâ¨. ¥®à¥¬ |
¤ã «ì®á⨠|
|
|
|||||||||||
«ï ¨áá«¥¤®¢ ¨ï ¡«î¤ ¥¬®á⨠á¨á⥬ â ª¦¥ ¨¬¥¥âáï ¥á- |
|
||||||||||||||
ª®«ìª® íª¢¨¢ «¥âëå ªà¨â¥à¨¥¢. ç áâ®áâ¨, ¯® |
«®£¨¨ |
|
|||||||||||||
ᮠ᢮©á⢮¬ ¯.6 ã¯à ¢«ï¥¬®áâ¨ à ¢¥á⢮ CeAt x0 |
= 0 ¯à¨ |
|
|||||||||||||
¢á¥å t t1 t2 t1 |
< t < t2 |
¢®§¬®¦® ⮫쪮 ¯à¨ x0 = 0: «¥¤®- |
|||||||||||||
¢ ⥫ì®, ¡«î¤ ï § |
¢ë室®¬ y(t) = Cx(t) â ª®© á¨á⥬ë |
|
|||||||||||||
¯à¨ ã«¥¢®¬ ¢å®¤¥, ¢á¥£¤ ¬®¦® ®¯à¥¤¥«¨âì, 室¨âáï «¨ |
|
||||||||||||||
á¨á⥬ |
¢ á®áâ®ï¨¨ à ¢®¢¥á¨ï. |
|
|
|
|
|
|
|
|
||||||
à㣨¬ ªà¨â¥à¨¥¬ ¯®«®© ¡«î¤ ¥¬®á⨠ï¥âáï à - |
|
||||||||||||||
¢¥á⢮ rankQ = n £¤¥ n { à §¬¥à®áâì ¯à®áâà á⢠á®- |
|
||||||||||||||
áâ®ï¨© á¨á⥬ë, Q |
{ |
¬ âà¨æ ¡«î¤ ¥¬®áâ¨, |
|
T |
|
||||||||||
Q = [C |
|
||||||||||||||
AT CT |
: : : (AT )n;1CT ] à §¬¥à n nl: ç áâ®áâ¨, ¤«ï MISO- |
||||||||||||||
á¨á⥬ (l = 1) ¬ âà¨æ |
¡«î¤ ¥¬®á⨠¤®«¦ ¡ëâì ¥¢ë- |
|
|||||||||||||
஦¤¥®©. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
«¨§¨àãï 㪠§ ë¥ ¢ëè¥ á¢®©á⢠, ã¡¥¦¤ ¥¬áï ¢ á¯à - |
|
||||||||||||||
¢¥¤«¨¢®áâ¨ â¥®à¥¬ë ¤ã «ì®á⨠«¬ , ᮣ« á® ª®â®à®© |
|
||||||||||||||
¨§ ¯®«®© ã¯à ¢«ï¥¬®á⨠¯ àë (A B) á«¥¤ã¥â ¯®« ï ¡- |
|
||||||||||||||
«î¤ ¥¬áâì ¯ àë (AT BT ), ¨, ®¡®à®â, ¨§ ¯®«®© ¡«î- |
|
||||||||||||||
¤ ¥¬®á⨠¯ àë (A C) á«¥¤ã¥â ¯®« ï ã¯à ¢«ï¥¬®áâì ¯ àë |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
~ ~ |
|
|
|
¢á¥£¤ ¢ë¯®«¥- |
|
||||
|
®« ï ã¯à ¢«ï¥¬®áâì ¯ àë (A B) 㪠§ ®£® ¢¨¤ |
|
|||||||||||||
. í⮬ ¬®¦® ã¡¥¤¨âìáï ¥¯®á।áâ¢¥ë¬ ¨á¯®«ì§®¢ ¨¥¬ ªà¨â¥à¨ï ¯.1.
174
(AT CT ): ®í⮬㠥⠥®¡å®¤¨¬®á⨠à áᬠâਢ âì ¢á¥ ªà¨- â¥à¨¨ ¯®«®© ¡«î¤ ¥¬®áâ¨, ¤®áâ â®ç® ¢ ä®à¬ã«¨à®¢ª å ªà¨â¥à¨¥¢ ã¯à ¢«ï¥¬®á⨠¯à®¨§¢¥á⨠§ ¬¥ã A AT ¨ B CT :
âáî¤ , ¢ ç áâ®áâ¨, ¯®«ãç ¥¬, çâ® ¯®«®áâìî ¡«î¤ - ¥¬ãî á¨á⥬㠥«ì§ï ¯à¨¢¥á⨠¥¢ë஦¤¥ë¬ ¯à¥®¡à §®¢ - ¨¥¬ ª ¢¨¤ã
~ |
A11 |
0n1 n2 |
~ |
|
A = A21 |
A22 |
C = C1.0l n2 n = n1 |
+ n2: |
|
ï ¯ à |
¬ âà¨æ ®¡« ¤ ¥â ⥬ ᢮©á⢮¬, çâ® ã ᮮ⢥â- |
|||
áâ¢ãî饩 á¨áâ¥¬ë ¨¬¥îâáï ª®¬¯®¥âë ¢¥ªâ®à |
á®áâ®ï¨ï, |
|||
ª®â®àë¥ ¨ ¯àאַ, ¨ ª®á¢¥® (ç¥à¥§ ¤à㣨¥ ª®¬¯®¥âë) ¥
ãç áâ¢ãîâ ¢ ä®à¬¨à®¢ ¨¨ ¢ë室®£® ¯à®æ¥áá . |
|
® «®£¨¨ ᮠ᢮©á⢮¬ ã¯à ¢«ï¥¬®á⨠ãà ¢¥¨ï á ¬ - |
|
~ |
~ |
âà¨æ ¬¨ A ¨ |
C 㪠§ ®£® ¢¨¤ §ë¢ îâáï ª ®¨ç¥áª®© |
ä®à¬®© ¡«î¤ ¥¬®á⨠[47, 174]. ®®â¢¥âáâ¢ãîé ï áâàãªâãà-
ï á奬 |
¯à¨¢¥¤¥ à¨á. 7.3, ¡). |
|||
|
«¥¥, ¤«ï ¯®«®áâìî ¡«î¤ ¥¬®© MISO-á¨á⥬ë (y(t)2 |
|||
R |
) ¢á¥£¤ |
©¤¥âáï n 1-¬ âà¨æ B â ª ï, çâ® ¯¥à¥¤ â®ç ï |
||
|
|
;1 |
B { ¥á®ªà ⨬ ï ¤à®¡ì á® á⥯¥- |
|
äãªæ¨ï W(s) = C(sI ; A) |
|
|||
ìî § ¬¥ ⥫ï, à ¢®© n: |
ª¨¬ ®¡à §®¬, ¥âà㤮 ¯®ª - |
|||
§ âì, çâ® ¥á®ªà ⨬®áâì ¯¥à¥¤ â®ç®© äãªæ¨¨ ¯à¨ m = l = 1 ï¥âáï ¥®¡å®¤¨¬ë¬ ¨ ¤®áâ â®çë¬ ãá«®¢¨¥¬ ¥¢ëà®- ¦¤¥®á⨠SISO-á¨á⥬.
®¡é¥¬ á«ãç ¥ MIMO-á¨á⥬ ¥¢ë஦¤¥®áâì á¨á⥬ë ᮮ⢥âáâ¢ã¥â ¢ë¯®«¥¨î á«¥¤ãî饣® ãá«®¢¨ï ¤«ï ¯¥à¥¤ -
â®çëå ¬ âà¨æ [30]. |
|
|
«ï «î¡®£® ᮡá⢥®£® ç¨á« |
¬ âà¨æë A áãé¥áâ¢ã¥â â - |
|
ª®© ¬¨®à M(s) ¬ âà¨æë W(s) çâ® |
|
|
lim A(s)M (s) = 0 |
(7.6) |
|
s!si |
6 |
|
£¤¥ A(s) = det(sIn ; A) { å à ªâ¥à¨áâ¨ç¥áª¨© ¬®£®ç«¥ ¬ - âà¨æë A: «ï SIMO ¨ MISO-á¨á⥬ í⮠᢮©á⢮ ®§ ç ¥â ¥-
¢®§¬®¦®áâì ¯à¥¤áâ ¢«¥¨ï W(s) ¢ ¢¨¤¥ ®â®è¥¨ï ¤¢ãå ¬®- £®ç«¥®¢ (¬ âà¨ç®£® ¨ ᪠«ïண®) á® á⥯¥ìî § ¬¥ â¥- «ï ¬¥ì襩, 祬 n: ¥¢ë஦¤¥®áâì ¯¥à¥¤ â®ç®© äãªæ¨¨ ¤«ï SISO-á¨á⥬ ¢ë⥪ ¥â ®âáî¤ ª ª ç áâë© á«ãç ©.
஢¥àªã ãá«®¢¨ï ¥¢ë஦¤¥®á⨠MIMO-á¨á⥬ ¬®¦- ® ã¯à®áâ¨âì, ¥á«¨ ¢®á¯®«ì§®¢ âìáï á«¥¤ãî騬 १ã«ìâ ⮬ [30].
175
«ï ¯®«®© ã¯à ¢«ï¥¬®á⨠á¨á⥬ë (A B) ¥®¡å®¤¨¬® ¨ ¤®áâ â®ç®, çâ®¡ë ¤«ï «î¡®£® ª®àï si ¬®£®ç«¥ A(s) = det(sIn ; A) ã ¬ âà¨æë W(s) 襫áï ¡ë â ª®© ¬¨®à M (s) ¯®à浪 , à ¢®£® ¤¥ä¥ªâã d ¬ âà¨æë (siIn ;A) çâ® ¢ë¯®«¥® (7.6).
|
|
¬ ¥ ç ¨ ¥ . ãáâì rB = rank(B) |
rC = rank(C): |
ëè¥ ®â¬¥ç¥®, çâ® ¥á«¨ å®âï ¡ë ¤«ï ®¤®£® ª®àï si ¢ë¯®«-
¥® d > rB â® á¨á⥬ (A B) ¥ã¯à ¢«ï¥¬ , ¥á«¨ d > rC â® á¨á⥬ (A C) ¥ ¡«î¤ ¥¬ . ®í⮬㠯¥à¥¤ â®ç ï ¬ - âà¨æ W(s) ¬®¦¥â ¡ëâì ¥¢ë஦¤¥®© «¨èì ¯à¨ d rB ¨ d rC : ç¨â, ãá«®¢¨¥ (7.6) ¨¬¥¥â á¬ëá« ¯à®¢¥àïâì «¨èì ¯à¨ ¢ë¯®«¥¨¨ 㪠§ ëå ¥à ¢¥á⢠¨ ¤«ï ¬¨®à®¢ M(s) ¯®à浪 d: ᫨ ¤¥ä¥ªâ d ¥¨§¢¥áâ¥, â® (7.6) á«¥¤ã¥â ¯à®-
¢¥àïâì «¨èì ¤«ï ¬¨®à®¢, ¯®à冷ª ª®â®àëå ¥ ¯à¥¢®á室¨â maxfrB rC pig £¤¥ pi { ªà â®áâì ª®àï si [30].
®¤¯à®áâà á⢮ ¥ ¡«î¤ ¥¬ëå á®áâ®ï¨© á¨áâ¥¬ë ¯à¥¤- áâ ¢«ï¥â ᮡ®© ã«ì-¯à®áâà á⢮ ¬ âà¨æë QT â.¥. ï¥âáï
x = 0: ᫨ á¨á⥬ ¯®«®áâìî
¡«î¤ ¥¬ , â® íâ® ¯®¤¯à®áâà á⢮ ¢ë஦¤ ¥âáï ¢ â®çªã x = 0: T
«ï ¯à®¢¥àª¨ ®à¬ «ì®á⨠á¨á⥬ë á«¥¤ã¥â ¢®á¯®«ì§®- ¢ âìáï ªà¨â¥à¨¥¬ ã¯à ¢«ï¥¬®á⨠¤«ï ¬ âà¨æ A bi £¤¥ bi
i = 1 : : : m { á⮫¡æë ¬ âà¨æë B:
«ï ¯à®¢¥àª¨ ã¯à ¢«ï¥¬®á⨠¯® ¢ë室 ¬ ¬®¦® ¨áá«¥¤®-
¢âì à £ ¬ âà¨æë L = [CB CAB : : : CAn;1B] [88].
áᬮâਬ ¯à¨¬¥à ¯à¥®¡à §®¢ ¨ï ç áâ¨ç® ¡«î¤ ¥- ¬®© á¨áâ¥¬ë ª ª ®¨ç¥áª®© ä®à¬¥ ¡«î¤ ¥¬®áâ¨. «ï íâ®- £® ¢¥à¥¬áï ª ®¯¨á ®© ¢ ¯. 1.4.3. á. 31 «¨¥ ਧ®¢ ®© ¬®¤¥«¨ ®¡à 饮£® ¬ ï⨪ .
ª ®â¬¥ç¥® á. 94 ¢ ¯. 3.2.4. ¬ âà¨æ ¡«î¤ ¥¬®á⨠Q á¨á⥬ë (1.18) ¢ë஦¤¥ ï, á«¥¤®¢ ⥫ì®, ¤ ï á¨-
á⥬ ¥ ï¥âáï ¯®«®áâìî ¡«î¤ ¥¬®©. ਢ¥¤¥¬ ãà ¢- ¥¨ï á®áâ®ï¨ï ¬ ï⨪ ª ª ®¨ç¥áª®© ä®à¬¥ ¡«î¤ - ¥¬®áâ¨. ®á¯®«ì§ã¥¬áï ®¯¨á ®© á. 433 ਫ®¦¥¨ï 3 ¯à®æ¥¤ãன obsvf ¯ ª¥â MATLAB [139].
ª 㪠§ ® ¢ ®¯¨á ¨¨ ¯à®æ¥¤ãàë,
[Abar, Bbar, Cbar, T, K] = obsvf(A, B, C)
¢®§¢à é ¥â ¬ âà¨æë à §¡¨¥¨ï ¯à®áâà á⢠á®áâ®ï¨©
¯®¤¯à®áâà á⢠|
¡«î¤ ¥¬ëå ¨ ¥ ¡«î¤ ¥¬ëå á®áâ®ï- |
¨©. ᫨ ¬ âà¨æ |
¡«î¤ ¥¬®á⨠¯ àë (A C) ¨¬¥¥â à £ |
|
176 |

r n, ⮠室¨âáï ¯à¥®¡à §®¢ ¨¥ ¯®¤®¡¨ï á ¬ âà¨æ¥© T
â ª®¥, çâ® Abar |
= T AT |
|
Bbar |
= T B Cbar = CT |
|
¨ ¯à¥®¡à - |
||||||
|
|
|
;1 |
|
|
|
|
;1 |
|
|
|
|
§®¢ ï á¨á⥬ |
¨¬¥¥â ¢¨¤ 8 |
|
|
|
|
|
|
|
|
|||
Ano |
|
A12 |
|
|
Bno |
|
|
|
|
|
|
|
Abar = 0 |
|
Ao |
Bbar |
= Bo |
|
Cbar = [ 0 |
Co ] |
|
||||
£¤¥ ¯ à (Ao Co) { ¡«î¤ ¥¬ ï ¨ Co(sI |
; |
Ao);1Bo |
|
C(sI |
; |
|||||||
A);1B: |
|
|
|
|
|
|
|
|
|
|||
á¯à ¢¥¤«¨¢®á⨠í⮣® ã⢥ত¥¨ï ¤«ï ¤ ®£® ¯à¨¬¥-
ମ¦® ã¡¥¤¨âìáï á ¯®¬®éìî á«¥¤ãî饩 ¯à®£à ¬¬ë
A=[0, 1, 0, 0v 0,-k/M,0,0v 0,0,0,1v -g/L 1,0,g/L 1,0] B=[0v 1/Mv 0 v 0]v C=[-1 0 1 0]/L 1v
{ä®à¬¨à®¢ ¨¥ ¬ âà¨æ ãà ¢¥¨© á®áâ®ï¨ï ¬®¤¥«¨ (1.18)\
[n,d]=ss2tf(A,B,C,D,0)
{¢ëç¨á«¥¨¥ ¯¥à¥¤ â®ç®© äãªæ¨¨ ¨á室®© á¨á⥬ë\
[Abar,Bbar,Cbar,T,K] = obsvf(A,B,C)
{¯à¥®¡à §®¢ ¨¥ ª ª ®¨ç¥áª®© ä®à¬¥ ¡«î¤ ¥¬®áâ¨\
Co=Cbar(1,2:4), Bo=Bbar(2:4,1), Ao=Abar(2:4,2:4)
{ ¢ë¤¥«¥¨¥ ¡«î¤ ¥¬®© ¯®¤á¨á⥬ë\
[no,do]=ss2tf(Ao,Bo,Co,0,1) Qo=obsv(Ao,Co) do=det(Qo)
{ ¢ëç¨á«¥¨¥ ¬ âà¨æë ¡«î¤ ¥¬®á⨠¯®¤á¨á⥬ë (Ao Co)
¨®¯à¥¤¥«¨â¥«ï í⮩ ¬ âà¨æë.
१ã«ìâ â¥ à ¡®âë ¯à®£à ¬¬ë ¯®«ãç¥ë ¬ âà¨æë
A = 2 |
0 |
; |
1 |
0 |
0 |
3 B = 2 |
0 |
3 |
|||
~ |
6 |
0 |
|
0:5 0:5 11:6 |
7 |
~ |
6 |
0:71 |
7 |
||
|
4 |
~ |
|
|
;0:5 11:6 |
5 |
|
4 |
;0:71 |
5 |
|
|
|
0 |
0:5 |
|
|
|
|
||||
|
|
0 |
|
0 |
1 |
0 |
|
|
|
0 |
|
C = [0 0 0 1:68] |
K = [1 1 1 0]: |
|||||
6 |
0:71 |
0 |
0:71 |
0 |
7 |
|
; |
|
|
|
|
||
T = 2 |
|
0 |
0:71 |
0 |
0:71 3 : |
|
4 |
|
0 |
;0:71 |
0 |
0:71 |
5 |
|
|
0:71 |
0 |
0:71 |
0 |
|
8 ।¨ ¢®§¬®¦ëå ¬ âà¨æ T ¯à®æ¥¤ãà obsvf 室¨â ®à⮣® «ì-
ãî ¬ âà¨æã [53, 115], â ª çâ® T ;1 = T T . ¬¥â¨¬, çâ® ¯à®æ¥¤ãà obsvf ä®à¬¨àã¥â ¬ âà¨æë, ¨¬¥î騥 ¨®© ¯®à冷ª à §¬¥é¥¨ï ¡«®ª®¢, 祬
¯à¨¢¥¤¥ á. 175 ¤«ï ~ ~
A C:
177
®«ãç ¥¬ ®¤¨ ª®¢ë¥ (á â®ç®áâìî ¤® ᮪à é¥¨ï ¬®¦¨- ⥫ì s) ¯¥à¥¤ â®çë¥ äãªæ¨¨, ᮢ¯ ¤ î騥 á ¯¥à¥¤ â®ç®© äãªæ¨¥© ¨á室®© á¨á⥬ë (3.15), ¯à¨¢¥¤¥®© ¢ ç¨á«¥®¬ ¯à¨¬¥à¥ á. 93. âà¨æ ¡«î¤ ¥¬®áâ¨
|
Qo = 2 |
0 |
0 |
1:68 |
3 |
det Qo = ;2:34: |
|
0 |
1:68 |
0 |
|||
|
4 |
0:84 ;0:84 91:6 |
5 |
|
||
7.4. |
¤ ç¨ ¨ ã¯à ¦¥¨ï |
|
|
|||
1. |
®ª § âì, çâ® ¯à¥®¡à §®¢ ¨¥ ¡ §¨á ¥ ¨§¬¥ï¥â - |
|||||
¡«î¤ ¥¬®á⨠¨ ã¯à ¢«ï¥¬®á⨠á¨á⥬ë.
2.®ª § âì, ç⮠ᮡáâ¢¥ë¥ ç¨á« ¬ âà¨æ A11 A22 ¯à¨ ¯¥à¥å®¤¥ ª (7.2) (á. 170) ¨¢ ਠâë ®â®á¨â¥«ì® ¢ë¡®à
¬âà¨æë ¯à¥®¡à §®¢ ¨ï T [47].
3.®ª § âì, çâ® ¯®¤¯à®áâà á⢮ ã¯à ¢«ï¥¬ëå á®á-
â®ï¨© á¨á⥬ë (7.2), ª ª ¨ ¨á室®© á¨á⥬ë, ¯®à®¦¤ ¥âáï ᮡá⢥묨 ¢¥ªâ®à ¬¨ (á. 81), ᮮ⢥âáâ¢ãî騬¨ ¯®«îá ¬ ã¯à ¢«ï¥¬®áâ¨, â.¥. ᮡáâ¢¥ë¬ ç¨á« ¬ ¬ âà¨æë A11 ¢ (7.2) [47].
4. ä®à¬ã«¨à®¢ âì ªà¨â¥à¨© ã¯à ¢«ï¥¬®á⨠¤«ï ¬ - âà¨ç®£® ¤¨ää¥à¥æ¨ «ì®£® ãà ¢¥¨ï:
X_ (t) = AX(t) + X(t)B + CU (t)D
£¤¥ X(t) { n n- ¬ âà¨æ à¥è¥¨©\ U (t) { r m-¬ âà¨æ ¢å®¤®¢ (ã¯à ¢«¥¨©)\ A B C { n n D { m n-¬ âà¨æë ¯ à ¬¥â஢ [3].
5. áá«¥¤®¢ âì ã¯à ¢«ï¥¬®áâì ¯ àë (A B) ¯à¨ [3]
6 |
0 |
1 |
0 |
1 |
7 |
6 |
1 |
7 |
1 |
0 |
1 |
0 |
0 |
||||
A = 2 |
1 0 |
1 |
0 |
3 |
B = 2 |
0 |
3: |
|
4 |
0 |
1 |
0 |
1 |
5 |
4 |
1 |
5 |
|
|
|
|
|||||
6. ëç¨á«¨âì £à ¬¨ ã¯à ¢«ï¥¬®á⨠(7.3) W(0 1) ¤«ï á¨á⥬ë x(t) + x(t) = u(t):
7. ¤ ç ®¡ ®¡¥á¯¥ç¥¨¨ ª®¥ç®© ¤«¨â¥«ì®á⨠¯¥à¥- 室®£® ¯à®æ¥áá , [174]. áᬮâਬ ¤¨áªà¥âãî, ¯®«®áâìî ã¯à ¢«ï¥¬ãî á¨á⥬ã
x[k + 1] = Ax[k] + Bu[k] x[k]2Rn u[k]2R k = 0 1 2 : : : (7: .7) 178

§¢¥áâ®, çâ® íâ á¨á⥬ ¬®¦¥â ¡ëâì ¯à¨¢¥¤¥ ¢ á®áâ®ï- ¨¥ à ¢®¢¥á¨ï ¥ ¡®«¥¥, 祬 § n è £®¢. ©¤¥¬ ãà ¢¥¨ï «¨¥©®£® ॣã«ïâ®à ¢ ®¡à ⮩ á¢ï§¨.
) ãáâì Q { ¬ âà¨æ ã¯à ¢«ï¥¬®á⨠á¨á⥬ë (7.7). ¡®- |
|||
§ 稬 ç¥à¥§ riT |
i-î áâப㠬 âà¨æë Q;1 â ª çâ® |
||
|
|
r1T |
3 : |
|
Q;1 = 2 r2T |
||
|
6 |
. |
7 |
|
rnT |
||
®ª § âì, çâ® ã¯à ¢«¥¨¥ u[k] =4;rnT5;kAnx[0] k = 0 1 2 : : : n; |
|||
1 ¯à¨¢¥¤¥â á¨á⥬ã (7.7) ¢ á®áâ®ï¨¥ à ¢®¢¥á¨ï § ªà âç ©- |
|||
襥 ¢à¥¬ï.
|
T |
|
|
¡) ¡®§ 稬 K = rn An: ®ª § âì, çâ® ®¡à â ï á¢ï§ì |
|||
u = ;Kx ¯à¨¢®¤¨â ª â ª®¬ã ¦¥ १ã«ìâ âã, çâ® ¨ ã¯à ¢«¥¨¥ |
|||
¯. 7. . |
|
|
|
¢) ¬ªãâ ï á¨á⥬ |
®¯¨áë¢ ¥âáï ãà ¢¥¨¥¬ |
||
|
x[k + 1] = (A ; BK)x[k]: |
|
|
ãáâì ¢á¥ á®¡áâ¢¥ë¥ ç¨á« ¬ âà¨æë A ; BK à ¢ë ã«î. |
|||
ª®¢ ¦®à¤ ®¢ |
ä®à¬ |
í⮩ ¬ âà¨æë? |
|
8. áᬮâà¥âì á¨á⥬ã (7.7) á ¬ âà¨æ ¬¨ [174] |
|||
2 |
1 |
0 |
1 |
A = 0 2 |
¨ B1 = 1 B2 |
= 0 : |
|
) «ï B1 ¨ B2 ¨áá«¥¤®¢ âì ã¯à ¢«ï¥¬®áâì á¨á⥬ë. |
|||
¡) «ï ¯®«®áâìî ã¯à ¢«ï¥¬ëå á¨á⥬ ©â¨ ã¯à ¢«ïî-
éãî ¯®á«¥¤®¢ ⥫ì®áâì, ª®â®à ï ¯à¨¢®¤¨â á¨á⥬㠪 ã«¥-
21 :
9. ãáâì ¢á¥ á®¡áâ¢¥ë¥ ç¨á« si ¬ âà¨æë A á¨á⥬ë
x(t) = Ax(t)+ Bu(t) u(t)2R ®¤¨ ª®¢ë ¨ à ¢ë [174]. ®ª |
- |
§ âì, çâ® á¨á⥬ ï¥âáï ¯®«®áâìî ã¯à ¢«ï¥¬®© ¢ ⮬, ¨ |
|
⮫쪮 ⮬, á«ãç ¥, ª®£¤ ¬ âà¨æ A á®á⮨⠨§ ¥¤¨á⢥®©
¦®à¤ ®¢®© ª«¥âª¨, ¬ âà¨æ B (¢ ⮬ ¦¥ ¡ §¨á¥) ¨¬¥¥â ¥- ã«¥¢®© í«¥¬¥â ¢ ¯®á«¥¤¥© áâப¥. ®ª § âì áâàãªâãàãî á奬㠤«ï ¨â¥à¯à¥â 樨 ¯®«ã祮£® १ã«ìâ â .
10. ®ª § âì, çâ® ®¡à â ï á¢ï§ì ¯® á®áâ®ï¨î ¥ - àãè ¥â ã¯à ¢«ï¥¬®áâ¨, ¨¬¥®, ¥á«¨ á¨á⥬ (7.7) ¯®«®- áâìî ã¯à ¢«ï¥¬ , â® ¯®«®áâìî ã¯à ¢«ï¥¬®© ¡ã¤¥â ¨ á¨áâ¥- ¬ x[k + 1] = (A ; BK)x[k] + Bu[k] [174]. ( ª § ¨¥: ०¤¥,
179
祬 ¨á¯®«ì§®¢ âì à £®¢ë© ªà¨â¥à¨© ã¯à ¢«ï¥¬®áâ¨, ®¡à -
â¨âìáï ª ®¯à¥¤¥«¥¨î ã¯à ¢«ï¥¬®áâ¨.) |
|
|
||||
|
11.. ãáâì £à¥£¨à®¢ ï á¨á⥬ |
§ ¤ |
ãà ¢¥¨ï¬¨ |
|||
[174] |
|
|
|
|
||
|
|
w(t) |
A11 A12 |
w(t) |
||
|
|
y(t) = |
A21 A22 = y(t) |
|||
¨ ¢ë室 y(t) { ¯®«®áâìî ¡«î¤ ¥¬ë©. ®ª § âì, çâ® ¯ à |
||||||
(A11 |
A21) ¯®«®áâìî ¡«î¤ ¥¬ . ( ª § ¨¥: ¤«ï ã¯à®é¥¨ï |
|||||
à áá㦤¥¨© ¬®¦® ¯®ª § âì ¯®«ãî ã¯à ¢«ï¥¬®áâì ¤ã «ì- |
||||||
®© á¨á⥬ë, á¬. á. 174). |
|
|
|
|||
|
12. áᬮâਬ ¤¢¥ ¤¨ ¬¨ç¥áª¨¥ á¨á⥬ë [174] |
|||||
|
x1(t) = x2 (t) + u(t) |
|
x3(t) = x3(t) + w(t) |
|||
S1 : |
x2 |
(t) = ;2x1(t) ; 3x2(t) |
S2 : |
|||
z(t) = x3(t) |
||||||
|
y(t) = x1(t) + x2 (t) |
|
|
|||
£¤¥ { ¯ à ¬¥âà.
) áá«¥¤®¢ âì ãá⮩稢®áâì, ã¯à ¢«ï¥¬®áâì, ¡«î¤ ¥- ¬®áâì á¨á⥬ S1 S1:
¡) ਠ¯®á«¥¤®¢ ⥫쮬 ᮥ¤¨¥¨¨ á¨á⥬ (w(t) = y(t)) ¯®«ãç ¥âáï á¨á⥬ S3: áá«¥¤®¢ âì ãá⮩稢®áâì, ã¯à ¢«ï- ¥¬®áâì ¨ ¡«î¤ ¥¬®áâì í⮩ á¨á⥬ë.
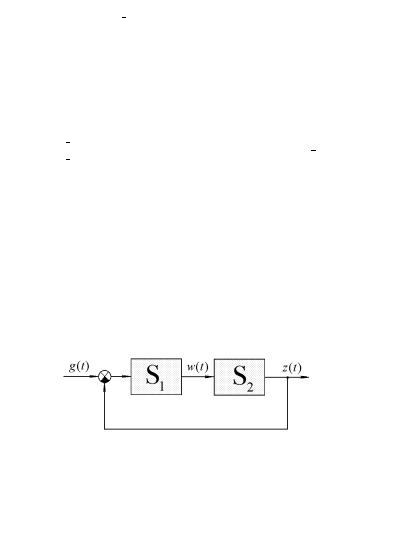
¢) ਠᮥ¤¨¥¨¨ á ®¡à ⮩ á¢ï§ìî ¯®«ãç ¥âáï á¨á⥬ S4 (á¬. à¨á. 7.4). ஢¥á⨠㪠§ ë¥ ¨áá«¥¤®¢ ¨ï ¤«ï í⮩ á¨á⥬ë.
¨á. 7.4. âàãªâãà ï á奬 ª § ¤ ç¥ 12 ¢).
180
8.-
8.1. ®áâ ®¢ª § ¤ ç¨ ®æ¥¨¢ ¨ï á®áâ®ï¨ï
áâ®ï饬 ¯ à £à ä¥ ¯à¨¢®¤ïâáï ¥ª®â®àë¥ á¢¥¤¥¨ï ¨§ ⥮ਨ ®æ¥¨¢ ¨ï. áᬠâਢ îâáï § ¤ ç ¯®«ãç¥¨ï ¨- ä®à¬ 樨 ® á®áâ®ï¨¨ á¨áâ¥¬ë ®á®¢¥ ¨§¬¥à¥¨© ⮫쪮 ¥¥ ¢å®¤ ¨ ¢ë室 ¨, ªà®¬¥ ⮣®, § ¤ ç ®æ¥¨¢ ¨ï ¢®§¬ã-
饨©.
ਠ«¨ç¨¨ ¨ä®à¬ 樨 ® ⥪ãé¨å § 票ïå ¯¥à¥¬¥- ëå á®áâ®ï¨ï ®¡ê¥ªâ ¬®¦¥â ¡ëâì à¥è¥ § ¤ ç ¬®¤ «ì- ®£® ã¯à ¢«¥¨ï { ®¡¥á¯¥ç¥¨ï § ¤ ëå § 票© ª®íää¨- 樥⮢ å à ªâ¥à¨áâ¨ç¥áª®£® ¬®£®ç«¥ . ஬¥ ⮣®, à¥è¥- ¨¥ à §«¨çëå § ¤ ç ®¯â¨¬ «ì®£® ã¯à ¢«¥¨ï ¯à®æ¥áá ¬¨ ®á®¢ ® ¨á¯®«ì§®¢ ¨¨ § 票© ¢á¥£® ¢¥ªâ®à á®áâ®ï- ¨ï. ªâ㠫쮩 ï¥âáï â ª¦¥ § ¤ ç ®æ¥¨¢ ¨ï ¥¨§¬¥- à塞ëå ¢®§¬ã饨© ¤«ï ®à£ ¨§ 樨 ª®¬¡¨¨à®¢ ®£® ã¯à - ¢«¥¨ï. ॠ«ìëå ãá«®¢¨ïå ¨§¬¥à¥¨¥ ¢¥ªâ®à á®áâ®ï¨ï, ª ª ¯à ¢¨«®, ¥®áãé¥á⢨¬® ¨§-§ ¥®¡å®¤¨¬®á⨠ãáâ ®¢ª¨
¤ вз¨ª®¢ ¢ ва㤮¤®бвг¯ле ¬¥бв е, ¨§¬¥а¥¨п ¯а®¨§¢®¤ле ¢лб®ª¨е ¯®ап¤ª®¢ ¨ в ª ¤ «¥¥. й¥ ¡®«¥¥ б«®¦®© § ¤ з¥© п¢«п¥вбп ¨§¬¥а¥¨¥ ¢®§¬гй¥¨©. а¥®¤®«¥вм (¨«¨ г¬¥м- и¨вм) нв¨ ва㤮бв¨ ¬®¦®, ¥б«¨ ¨¡®«¥¥ ¯®«® ¨б¯®«м§®- ¢ вм ¨¬¥ойгобп ¯а¨®аго ¨д®а¬ ж¨о ® ¬®¤¥«¨ ®¡к¥ªв ¨ в¥ªгй¨¥ ¨§¬¥а¥¨п ¥£® ¢е®¤®¢ ¨ ¢л室®¢. нв®© ж¥«мо ¢
á¨á⥬ã ã¯à ¢«¥¨ï ¢¢®¤¨âáï ¯®¤á¨á⥬ ( «£®à¨â¬) ®æ¥¨- ¢ ¨ï á®áâ®ï¨ï ®¡ê¥ªâ ¨ ¢®§¬ã饨© [3, 8, 47, 76, 88, 93].
§«¨ç îâ âਠ⨯ ®æ¥®ª á®áâ®ï¨ï:
ᣫ ¦¨¢ ¨¥ { ¯® ⥪ã騬 ¤ ë¬ ®¯à¥¤¥«ï¥âáï ¯®¢¥- ¤¥¨¥ á¨áâ¥¬ë ¢ ¯à®è«®¬, â.¥. ¯® १ã«ìâ â ¬ ¨§¬¥à¥¨© ª ¬®¬¥â㠢६¥¨ t ®æ¥¨¢ ¥âáï á®áâ®ï¨¥ á¨áâ¥¬ë ¬®¬¥â
t ; T T > 0\ |
|
䨫ìâà æ¨ï { ¯® ⥪ã騬 ¤ ë¬ ®¯à¥¤¥«ï¥âáï á®áâ®- |
|
逸 á¨áâ¥¬ë ¢ â®â ¦¥ á ¬ë© ¬®¬¥â ¢à¥¬¥¨\ |
|
¯à®£®§ { ¯à®¨§¢®¤¨âáï íªáâà ¯®«ïæ¨ï १ã«ìâ ⮢ ¨§- |
|
¬¥à¥¨©, â.¥. ¯® ¤ ë¬ ª ¬®¬¥â㠢६¥¨ t |
®æ¥¨¢ ¥âáï |
á®áâ®ï¨¥ á¨áâ¥¬ë ¢ ¡ã¤ã饬, ¬®¬¥â t + T |
T > 0: |
ª¨¬ ®¡à §®¬, ®æ¥¨¢ ¨¥ ï¥âáï § ¤ 祩 ¢®ááâ ®¢«¥- ¨ï á®áâ®ï¨ï á¨áâ¥¬ë ¯® ¤®áâ㯮© ⥪ã饩 ¨ä®à¬ 樨 ® ¥¥ ¢å®¤ å ¨ ¢ë室 å. â § ¤ ç ¯à¨æ¨¯¨ «ì® à §à¥è¨-
181
