
Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления
.pdf(2.15), £¤¥ ¢¬¥áâ® n 1-¬ âà¨æë B ¨á¯®«ì§ã¥âáï n l-¬ âà¨æ
B = 2 |
|
. |
|
3 |
|
1 1 |
1 2 : : : 1 m |
|
|
4 |
n 1 |
n 2 : : : n m 5 |
||
ª®íää¨æ¨¥âë i j |
i = 1 : : : n j = 1 : : : m ¢лз¨б«повбп ¯® |
|||
ä®à¬ã«¥ (4.4) ¤«ï ª ¦¤®£® ¬®£®ç«¥ |
Bj(s): |
|||
«¥¤®¢ ⥫ì®, ¥á«¨ ¨¬¥¥âáï á¨á⥬ |
á ®¤¨¬ ¢å®¤®¬, ª®- |
|||
â®àë© "à §¢¥â¢«ï¥âáï" |
¥áª®«ìª® ¢ë室®¢, 楫¥á®®¡à §® |
|||
¨á¯®«ì§®¢ âì , |
¥á«¨ ¥áª®«ìª® ¢å®¤ëå ᨣ «®¢ ¤¥©- |
|||
бв¢гов б¨бв¥¬г ¨ ¢ле®¤л¥ а¥ ªж¨¨ б㬬¨аговбп, { д®а- ¬г . ¡й¨© б«гз © MIMO-б¨бв¥¬ п¢«п¥вбп бгй¥бв¢¥- ® ¡®«¥¥ б«®¦л¬. а¥¦¤¥ з¥¬ ®¡б㦤 вм ¥£®, а бᬮва¨¬ ¯а¨¢¥¤¥¨¥ ¯¥а¥¤ в®зле дгªж¨© ª га ¢¥¨п¬ б®бв®п¨п, ¯а¥¤бв ¢«¥л¬ ¤¨ £® «м®© (¦®а¤ ®¢®©) д®а¬®© ¬ ва¨-
æë A:
4.3. «®ç®-¤¨ £® «ì ï ä®à¬
áᬮâਬ SISO-á¨á⥬ã, § ¤ ãî ¯¥à¥¤ â®ç®© äãªæ¨¥© (4.1). ãáâì ¨§¢¥áâë ª®à¨ å à ªâ¥à¨áâ¨ç¥áª®£® ¬®£®ç«¥- , ª®â®àë¥ ¢ ç «¥ ¯à¥¤¯®« £ ¥¬ ¯à®áâ묨. í⮬ á«ãç ¥ ¢á¥£¤ ¨¬¥¥âáï ¢®§¬®¦®áâì à §«®¦¨âì W(s) ¯à®á⥩訥
á« £ ¥¬ë¥ ¯¥à¢®£® ¨ ¢â®à®£® ¯®à浪®¢, â.¥. |
§ ¯¨á âì ¥¥ ¢ |
|||||||||
¢¨¤¥ (2.5), ª ª W(s) = q+r Wi(s) £¤¥ |
|
|
|
|||||||
|
|
|
|
i=1 |
|
|
|
|
|
|
Wi(s) = 8 |
|
|
P Ki |
|
|
|
i = 1 : : : q |
|||
|
|
|
|
|
|
|||||
|
d0 |
s + d s ; si |
|
|
||||||
> |
|
|
j |
j |
|
j = i |
; |
q |
i=q+1 : : : q +r: |
|
|
|
2 js + j2 + j2 |
||||||||
< s2 |
|
|
|
|
||||||
> |
|
; |
|
|
|
|
|
|
|
|
«ï ª ¦¤®: £® á« £ ¥¬®£® (¢ ¯à®¨§¢®«ì® ¢ë¡à ®¬ ¯®àï¤-
ª¥) § ¯®«повбп ª«¥вª¨ ¬ ва¨жл A, ¨¬¥î饩 ¢¥é¥á⢥ãî
102

ä®à¬ã ®à¤ (2.4)
2 |
s1 |
0 |
0 |
: : : |
: : : |
|
|
|
0 |
3 |
0 |
s2 |
0 |
: : : |
: : : |
|
|
|
0 |
||
|
. |
|
... |
: : : |
|
|
|
. |
|
|
|
0 |
: : : |
0 |
sq |
0 |
: : : |
|
|
0 |
|
A = 0 : : : : : : 0 |
1 |
1 |
: : : |
0 |
: |
|||||
|
0 |
: : : |
: : : 0 |
; 1 |
1 |
: : : |
0 |
|
||
4 |
. |
|
|
... |
|
. .. |
; |
|
. |
5 |
6 |
0 |
0 : : : |
0 |
0 |
r |
r |
|
|||
0 |
0 : : : |
0 |
0 |
|
r |
r 7 |
||||
«¥¬¥âë n 1-¬ âà¨æë B ¨ 1 n-¬ âà¨æë C 室ïâáï â ª¨¬ ®¡à §®¬, ç⮡ë ᮮ⢥âáâ¢ãîé ï ¤ ®¬ã ¢å®¤ã ¯¥à¥¤ â®ç-
ï äãªæ¨ï ¨§ (2.5) ¨¬¥« |
|
§ ¤ ë¥ ª®íää¨æ¨¥âë ç¨á«¨â¥- |
||||||
«ï. 4 ᫨ Wi(s) = |
Ki |
|
|
⮠ᮮ⢥âáâ¢ãî騥 í«¥¬¥âë |
||||
|
|
|
||||||
|
s ; si |
|
|
|
|
|
||
¤®«¦ë 㤮¢«¥â¢®àïâì ãá«®¢¨î bici = Ki: «ï ¡«®ª®¢ ¢â®à®- |
||||||||
£® ¯®à浪 á ¯¥à¥¤ â®ç®© äãªæ¨¥© |
|
|
||||||
|
|
|
|
|
d0 |
s + d |
|
|
Wj(s) = |
|
|
|
j |
j |
|
|
|
s2 |
; |
2 js + 2 |
+ 2 |
|||||
|
|
|
|
|
j |
j |
||
|
|
|
|
|
|
|||
ª®íää¨æ¨¥âë ç¨á«¨â¥«ï d0j dj á¢ï§ ë á í«¥¬¥â ¬¨ ¬ âà¨æ B C á®®â®è¥¨ï¬¨
d0j = c1b1 + c2b2 dj = c1(b2 j ; b1 j) ; c2(b1 j + b2 j):
⨠ãá«®¢¨ï ¤ îâ ¢®§¬®¦®áâì ¢ë¡à âì ¨áª®¬ë¥ í«¥¬¥âë, ¯à¨ç¥¬ § ¤ ç â ª¦¥ à¥è ¥âáï ¥®¤®§ ç®. ®¦®, - ¯à¨¬¥à, ४®¬¥¤®¢ âì ¨á¯®«ì§®¢ âì á«¥¤ãî騥 § 票ï: b1 = 0 b2 = 1 c1 = jd0j j+ dj
4.4. ®à¤ ®¢ ä®à¬
᫨ ¯¥à¥¤ â®ç ï äãªæ¨ï á¨áâ¥¬ë ¨¬¥¥â ªà âë¥ ¯®«î- á , ¥¥ à §«®¦¥¨¥ ¡ã¤¥â ᮤ¥à¦ âì á« £ ¥¬ë¥, á⥯¥¨ § - ¬¥ ⥫¥© ª®â®àëå ®â¢¥ç îâ § ç¥¨ï¬ ªà â®áâ¨. «ï ¢¥- é¥á⢥ëå ª®à¥© ªà â®á⨠k ¯®«ãç îâáï § ¬¥ ⥫¨ k-©
4 ¤¥áì ãç¨âë¢ ¥âáï, çâ® ¯à¨ ¡«®ç®-¤¨ £® «ì®© ä®à¬¥ ¬ âà¨æë A ª ¦¤ ï ¯®¤á¨á⥬ ¬®¦¥â à áᬠâਢ âìáï ¥§ ¢¨á¨¬® ®â ¤à㣨å.
103
á⥯¥¨, ¤«ï ¬¨¬ëå ª®à¥© { á⥯¥¨ 2k: ®£¤ W(s) ¨¬¥¥â ¢¨¤ (2.5), (2.9). áå®¤ï ¨§ ©¤¥ëå ¯à¨ à §«®¦¥¨¨ ¯¥- । â®ç®© äãªæ¨¨ W(s) á« £ ¥¬ëå Wi(s) 㪠§ ®£® ¢¨¤ ¥âà㤮 § ¯¨á âì ¬ âà¨æã A ¢ ä®à¬¥ ®à¤ (2.6), ¢ ª®â®- ன ¢¥é¥áâ¢¥ë¬ ª®àï¬ á®®â¢¥âáâ¢ãîâ ¤¨ £® «ìë¥ ¡«®- ª¨ ¢¨¤ (2.7), ¬¨¬ë¬ { ¡«®ª¨ ¢¨¤ (2.8). «¥¬¥âë ¬ âà¨æ B C ¬®¦® ¯®«ãç¨âì ¯ã⥬ ®¡à âëå ¢ëç¨á«¥¨© ¬¥â®¤®¬ ¥®¯à¥¤¥«¥ëå ª®íää¨æ¨¥â®¢.
¯à¨¬¥à, ¤«ï ¢¥é¥á⢥ëå ª®à¥© s1j = s2j = : : :
(ªà â®á⨠kj) ¬®¦® ¯à¥¤áâ ¢¨âì Wj (s) ¢ ¢¨¤¥
|
kj |
; |
|
|
|
|
X |
|
|
||
Wj (s) = |
|
|
Kji |
|
|
i=1 |
(s skj )i |
: |
|
||
᫨ ¢ë¡à âì í«¥¬¥âë ᮮ⢥âáâ¢ãîé¨å áâப ¬ âà¨æë B |
|||||
¢ ¢¨¤¥ b1 = b2 = : : : = bkj;1 = 0 |
bkj |
= 1 ⮠ᮮ⢥âáâ¢ãî騥 |
|||
¤ ®© ª«¥âª¥ í«¥¬¥âë ¬ âà¨æë C |
®¯а¥¤¥«повбп а ¢¥бв¢ - |
||||
¬¨ ci = Kji : à㣮© ¢®§¬®¦ë© ¢ë¡®à { ¯®«®¦¨âì c1 |
= 1 |
||||
®áâ «ìë¥ í«¥¬¥âë ¯®¤áâப¨ { à ¢ë¬¨ ã«î. ®£¤ |
§ - |
||||
票ï Kji ¢§ïâë¥ ¢ ®¡à ⮬ ¯®à浪¥, ¯à¨á¢ ¨¢ îâáï í«¥- ¬¥â ¬ bi: ¢ë© ¢¨¤ ãà ¢¥¨© á®áâ®ï¨ï ¤«ï ¢¥é¥á⢥ëå ª®à¥© å à ªâ¥à¨áâ¨ç¥áª®£® ¬®£®ç«¥ A(s) ¯à¨¢¥¤¥ ¢ [94].
¬ ¥ ç ¨ ¥ 1. à®æ¥áá ¯à¥®¡à §®¢ ¨ï ¯¥à¥¤ â®ç®© äãªæ¨¨ ª ¡«®ç®-¤¨ £® «ì®© ¨ ¦®à¤ ®¢®© ä®à¬ ¬ áãé¥- á⢥® ¡®«¥¥ âà㤮¥¬®ª, 祬 ¯à¥®¡à §®¢ ¨ï ª ¢¨¤ã
¨«¨ , â ª ª ª á¢ï§ á à §«®¦¥¨¥¬ ¯¥à¥¤ â®ç®© äãª- 樨 á« £ ¥¬ë¥ ¨, á«¥¤®¢ ⥫ì®, á ¢ëç¨á«¥¨¥¬ ª®à¥©
åà ªâ¥à¨áâ¨ç¥áª®£® ¬®£®ç«¥ .
¬ ¥ ç ¨ ¥ 2. ਢ¥¤¥ë¥ ¯à®æ¥¤ãàë ¯à¨¬¥¨- ¬ë ¨ ª ॠ«¨§ã¥¬ë¬ á¨á⥬ ¬, ã ª®â®àëå degB(s) = degA(s):«ï ¨å ¨á¯®«ì§®¢ ¨ï ¤® á ç « ¯à¥®¡à §®¢ âì ¯¥à¥¤ -
â®çãî äãªæ¨î, ¢ë¤¥«¨¢ ¢ ¥© 楫ãî ç áâì ¯ã⥬ ¤¥«¥¨ï
¬®£®ç«¥®¢
~
W(s) B(s) = d + B(s): A(s) A(s)
®íää¨æ¨¥â d ®¡à §ã~¥â 1 1-¬ âà¨æã D ¢ (1.45), ¯¥à¥¤ â®ç- |
||
~ |
B(s) |
|
ï äãªæ¨ï W(s) = |
A(s) |
®ª §ë¢ ¥âáï áâண® ॠ«¨§ã¥¬®© ¨ |
¯à¨¢®¤¨âáï ª ãà ¢¥¨ï¬ á®áâ®ï¨ï ®¡ëçë¬ ®¡à §®¬. à¥- §ã«ìâ ⥠í⮣® ¯à¥®¡à §®¢ ¨ï 室ïâáï ¬ âà¨æë
104
¬ ¥ ç ¨ ¥ 3. ¥ª®â®àëå § ¤ ç å 㤮¡® ¯®-
«ãç âì ãà ¢¥¨ï á®áâ®ï¨ï ¥ ¤«ï ¢á¥© á¨á⥬ë (¯ãáâì |
¤ - |
¦¥ à §®¬ªã⮩), ¤«ï ®â¤¥«ìëå §¢¥ì¥¢ (¯®¤á¨á⥬). |
- |
¯à¨¬¥à, â ª ï á¨âã æ¨ï ¨¬¥¥â ¬¥áâ®, ª®£¤ á¨á⥬ § ¤ |
¢ |
¢¨¤¥ áâàãªâãன á奬ë. ª ¯à ¢¨«®, ¯¥à¥å®¤ ª ãà ¢¥¨- |
|
ï¬ á®áâ®ï¨ï §¢¥ì¥¢ ®ª §ë¢ ¥âáï áãé¥á⢥® ¡®«¥¥ ¯à®á- |
|
âë¬. «ï ⮣® çâ®¡ë ¯®«ãç¨âì ãà ¢¥¨ï á®áâ®ï¨ï ¢á¥© á¨á⥬ë, ¬®¦® ¨á¯®«ì§®¢ âì ¨§«®¦¥ë¥ ¢ ¯. 1.7. ¬¥â®¤ë ®¯à¥¤¥«¥¨ï ãà ¢¥¨© á®áâ®ï¨ï ¤«ï £à¥£¨à®¢ ëå á¨- á⥬. ¯à¨¬¥à, ¯à¨ á¨â¥§¥ æ¨ä஢ëå 䨫ìâ஢ ¯à¨¬¥ï¥â- áï "ª ᪠¤ ï ॠ«¨§ æ¨ï", ¯à¨ ª®â®à®© ¯¥à¥¤ â®ç ï äãª- æ¨ï á¨áâ¥¬ë ¯à¥¤áâ ¢«ï¥âáï ¢ ¢¨¤¥ ¯à®¨§¢¥¤¥¨ï ¯¥à¥¤ â®ç- ëå äãªæ¨© ¯¥à¢®£® ¨ ¢â®à®£® ¯®à浪®¢. à ¢¥¨ï á®áâ®ï- ¨ï ¤«ï í⮣® á«ãç ï ¯®«ãç îâáï ¯®á«¥¤®¢ ⥫ìë¬ ¯à¨¬¥- ¥¨¥¬ ¯à¨¢¥¤¥ëå ¢ 1.7. ä®à¬ã«.
¬ ¥ ç ¨ ¥ 4. ਢ¥¤¥ë¥ ¢ëè¥ ãà ¢¥¨ï à áᬮ- âà¥ë ¤«ï ¥¯à¥àë¢ëå á¨á⥬, ®¤ ª® ¨§«®¦¥ë¥ ¢ áâ®- ï饩 £« ¢¥ ª ®¨ç¥áª¨¥ ä®à¬ë ¨ ¬¥â®¤ë ¯®«ã票ï ãà ¢- ¥¨© á®áâ®ï¨ï ¯® ¯¥à¥¤ â®çë¬ äãªæ¨ï¬ á ®ç¥¢¨¤ë¬ ¨§- ¬¥¥¨¥¬ ®¡®§ 票© ¯à¨¬¥¨¬ë ¨ ª ¤¨áªà¥âë¬ á¨á⥬ ¬.
ਫ®¦¥¨¨ C. á. 435, ¯à¨¢¥¤¥ë ⥪áâë ¯à®£à ¬¬ ¯à¨¢¥¤¥¨ï ãà ¢¥¨© á®áâ®ï¨ï SIMO-á¨á⥬ ª ¢¨¤ã (¯à®£à ¬¬ tf2cf) ¨ MISO-á¨á⥬ ª ¢¨¤ã (¯à®£à ¬¬ tf2of).
4.5. «ãç © á¨á⥬ á ¥áª®«ìª¨¬¨ ¢å®¤ ¬¨ ¨ ¢ë室 ¬¨
®á¥¬áï ¢®¯à®á ®¯à¥¤¥«¥¨ï ¬¨¨¬ «ì®© ॠ«¨§ 樨 ¤«ï
MIMO-á¨á⥬, ¨¬¥îé¨å ¥áª®«ìª® ¢å®¤®¢ ¨ ¥áª®«ìª® ¢ë- 室®¢ (m > 1 l > 1): ¤ ç ¯®«ãç¥¨ï ¬¨¨¬ «ì®© ॠ- «¨§ 樨 ãà ¢¥¨© á®áâ®ï¨ï ¤«ï â ª¨å á¨á⥬ áãé¥á⢥® á«®¦¥¥ à áᬮâ८© ¢ëè¥, ¯®í⮬㠮£à ¨ç¨¬áï ¥ª®â®- à묨 ¯à¨¬¥à ¬¨. 5
ਬ¥à 1. ãáâì § ¤ ë ¬ âà¨çë¥ 2 2 ¯¥à¥¤ â®çë¥ äãªæ¨¨
|
1 |
|
1 |
|
|
1 |
|
0 |
|
|
s |
|
|
s |
|
||||
W1 (s) = s1 |
1 |
|
¨ W2 (s) = 0 |
1 |
: |
||||
s |
|||||||||
5 ®«¥¥ ¯®¤à®¡ë¥ ᢥ¤¥¨ï ® à¥è¥¨¨ í⮩ § ¤ ç¨ ¨¬¥îâáï ¢ à ¡®â å [1, 88, 174].
105

¥âà㤮 ãáâ ®¢¨âì, ç⮠ॠ«¨§ 樥© ¬¨¨¬ «ì®£® ¯®àï¤- |
||||
ª |
W1(s) ¡ã¤ãâ ãà ¢¥¨ï á®áâ®ï¨ï: |
|
|
|
|
x(t) = u1(t) |
y1 (t) = x(t) + u2 (t) y2 (t) = x(t) + u2(t): |
||
⨬ ãà ¢¥¨ï¬ ᮮ⢥âáâ¢ãîâ ¬ âà¨æë |
|
|
||
|
|
1 |
0 |
1 |
|
A1 = 0 B1 = [1 0] C1 = 1 D1 |
= 0 |
1 : |
|
á¢®î ®ç¥à¥¤ì ¯¥à¥¤ â®ç ï äãªæ¨ï W2(s) ¨¬¥¥â ¬¨¨- ¬ «ìãî ॠ«¨§ æ¨î ¢¨¤
|
x1 |
(t) = |
u1 |
(t) |
y1 |
(t) = x1 |
(t) |
|
|
|
|
x2 |
(t) = |
u2 |
(t) |
y2 |
(t) = x2 |
(t) |
|
|
|
ª®â®à®© ®â¢¥ç îâ ¬ âà¨æë |
|
|
|
|
|
|
||||
0 |
0 |
|
1 |
0 |
|
1 |
0 |
0 |
0 |
: |
A2 = 0 |
0 B2 = 0 |
1 C2 |
= 0 |
1 D2 = 0 |
0 |
|||||
ª ¢¨¤¨¬, ãà ¢¥¨ï á®áâ®ï¨ï áãé¥á⢥® ®â«¨ç îâáï: ¤ ¦¥ à §¬¥à®á⨠¢¥ªâ®à®¢ á®áâ®ï¨ï ã ¤ ëå á¨á⥬ ®ª - §ë¢ îâáï à §«¨ç묨. ë© ¯à¨¬¥à ¯®ª §ë¢ ¥â, çâ® ¯à¨ ¯¥à¥å®¤¥ ª ãà ¢¥¨ï¬ á®áâ®ï¨ï ¤«ï MIMO-á¨á⥬ á«¥¤ã- ¥â ãç¨âë¢ âì ¡®«¥¥ "⮪¨¥" ᢮©á⢠¬ âà¨çëå ¯¥à¥¤ - â®çëå äãªæ¨©, å à ªâ¥à¨áâ¨ç¥áª¨© ¬®£®ç«¥ ¬ âà¨æë
¯®«ãç ¥¬ëå ãà ¢¥¨© á®áâ®ï¨ï ¥®¡ï§ â¥«ì® á®¢¯ ¤ ¥â á ¬®£®ç«¥®¬ A(s) ¯®«ãç¥ë¬ ¢ ¢¨¤¥ ®¡é¥£® ªà ⮣® § - ¬¥ ⥫¥© ¯¥à¥¤ â®çëå äãªæ¨© Wi j(s):
ਬ¥à 2. [88]. ãáâì § ¤ ¬ âà¨ç ï ¯¥à¥¤ â®ç ï äãªæ¨ï
|
|
|
|
|
0:7 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
9s + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
W(s) = 2 |
0:4 |
|
|
3 : |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2:0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
4 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8s + 1 |
|
9s + 1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
||
ëç¨á«ïï ¬ âà¨çë¥ ¢ëç¥âë ¢ ¯®«îá å s1 = |
;9 |
s2 |
= ;8 |
|
|
|||||||||||||||||
¯®«ã稬 à §«®¦¥¨¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
0:7 0 |
|
|
1 |
|
|
0 0 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
||
W(s) = |
|
0 0:4 |
+ |
|
|
2 0 |
= |
|
M1+ |
|
M2 |
: |
||||||||||
9s + 1 |
8s + 1 |
9s + 1 |
8s + 1 |
|||||||||||||||||||
|
|
|
|
|
106 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
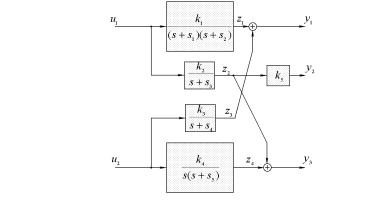
¨á. 4.1. âàãªâãà ï á奬 á¨áâ¥¬ë ¤«ï § ¤ ç¨ 2.
§¬¥à®áâì ¯à®áâà á⢠á®áâ®ï¨© ¬¨¨¬ «ì®© ॠ«¨§ - 樨 ®¯à¥¤¥«ï¥âáï, ª ª á㬬 à £®¢ ¬ âà¨æ M1 ¨ M2: ¤ - ®¬ ¯à¨¬¥à¥
0:7 |
0 |
rankM1 |
|
|
M1 = 0 |
0:4 |
= 2 M2 |
= |
á«¥¤®¢ â¥«ì® n = dimX = 3: âà¨æã £® «ì®© ä®à¬¥:
0 0 rankM2 = 1 2 0
A § ¯¨áë¢ ¥¬ ¢ ¤¨ -
|
2 |
|
|
;9 |
1 3 |
|
||||
|
|
|
1 |
0 |
0 |
|
|
|||
A = |
4 |
;9 |
|
1 |
|
|
5 |
: |
||
0 |
;8 |
|||||||||
0 |
||||||||||
|
0 |
|
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
«¥¥ ®¯à¥¤¥«ï¥¬ í«¥¬¥âë 3 2-¬ âà¨æë B ¨ 2 3-¬ âà¨æë C â ª, çâ®¡ë ¯®«ãç¨âì § ¤ ë¥ ç¨á«¨â¥«¨ W(s): ¥âà㤮 ã¡¥¤¨âìáï, ç⮠㪠§ ®¬ã ãá«®¢¨î 㤮¢«¥â¢®àïîâ ¬ âà¨æë
|
0:7 |
|
0 |
|
1 |
0 0 |
||
4 |
9 |
|
0:4 |
5 |
||||
4 |
|
|
|
|
||||
|
|
|
|
|||||
B = 2 |
|
01 |
|
|
09 |
3 C = 0 |
1 1 : |
|
|
|
|
||||||
áᬮâà¥ë© ¢ ਬ¥à¥ 2 ¬¥â®¤ ४®¬¥¤ã¥âáï ¤«ï á¨- á⥬, ¯¥à¥¤ â®çë¥ äãªæ¨¨ ª®â®àëå ¨¬¥îâ ⮫쪮 ¢¥é¥- áâ¢¥ë¥ ¯à®áâë¥ ¯®«îá [88]. ®¡é¥¬ á«ãç ¥ «£®à¨â¬ë ¯à¥®¡à §®¢ ¨ï ª ãà ¢¥¨ï¬ á®áâ®ï¨ï á«®¦¥¥ (á¬., ¯à¨- ¬¥à, [1], â ª¦¥ ਫ®¦¥¨¥ 2 ¢ [106]) ¨ §¤¥áì ¥ à áᬠâà¨- ¢ îâáï.
107
4.6. ¤ ç¨ ¨ ã¯à ¦¥¨ï
1. «ï á¨á⥬ë, § ¤ ®© ¯¥à¥¤ â®ç®© äãªæ¨¥©
W(s) = k( 1s + 1)( 2s + 1) s(T12 s2 + T2s + 1)
k = 10c;1 1 = 5c 2 = 0:2c T1 = 1c T2 = 5:2c ©â¨ ¬ âà¨- æë ãà ¢¥¨© á®áâ®ï¨ï ¢ ä®à¬¥ (2.12), (2.15) ¨ ¤¨ £® «ì®© (2.1). ª¨¥ ¨§ ¯®«ãç¥ëå ä®à¬ íª¢¨¢ «¥â- ë ¬¥¦¤ã ᮡ®© á â®ç®áâìî ¤® ¢ë¡®à ¡ §¨á ¯¥à¥¬¥ëå
á®áâ®ï¨ï?
2.®«ãç¨âì ¯¥à¥¤ â®çãî äãªæ¨î ¨ ãà ¢¥¨ï á®áâ®ï- ¨ï á¨á⥬ë á® áâàãªâãன á奬®© à¨á. 4.1 [94].
3.®ª § âì, çâ® ¯à¨ r = n á¨á⥬ã (4.1) ¬®¦® ¯à¨¢¥á⨠ª ¢¨¤ã ãà ¢¥¨© á®áâ®ï¨ï (1.45), £¤¥ D =6 0 (á¬. á®áªã 1 áâà ¨æ¥ 98).
108

5.-
®¯®«¨â¥«ìãî £«ï¤ãî ¨ä®à¬ æ¨î ® ¯®¢¥¤¥¨¨ á¨- á⥬ ¬®¦® ¯®«ãç¨âì à áᬮâ२¥¬ ¨å ä §®¢ëå ¯®àâà¥â®¢.¤¨¬ ®á®¢ë¥ ®¯à¥¤¥«¥¨ï ¨ à áᬮâਬ ®¡é¨¥ ᢮©áâ¢ ä §®¢ëå âà ¥ªâ®à¨© ¯à¨¬¥¨â¥«ì® ª «¨¥©ë¬ á¨á⥬ ¬.㤥¬ à áᬠâਢ âì ¢â®®¬ë¥ á¨á⥬ë, â.¥. â ª¨¥, ¢
га ¢¥¨п ª®в®але п¢® ¥ ¢е®¤¨в ¢а¥¬п. ª¨¬ ®¡а §®¬, ¡г- ¤¥¬ бз¨в вм, зв® ¯ а ¬¥вал б¨бв¥¬л ¥ ¬¥повбп ¢® ¢а¥¬¥- ¨ (б¨бв¥¬ бв ж¨® а ), в ª¦¥ зв® ¢е®¤®¥ ¢®§¤¥©бв¢¨¥ ®вбгвбв¢г¥в ¨ а бб¬ ва¨¢ вм в®«мª® б®¡бв¢¥л¥ ¤¢¨¦¥¨п б¨бв¥¬л
x(t) = Ax(t) |
x(0) = x0: |
(5.1) |
5.1.¯à¥¤¥«¥¨ï ¨ ®á®¢ë¥ ᢮©áâ¢ ä §®¢ëå âà ¥ª- â®à¨© ¨ ä §®¢ëå ¯®àâà¥â®¢
ਠ¯®áâ஥¨¨ ä §®¢ëå âà ¥ªâ®à¨© ª ¦¤®¬ã à¥è¥¨î áâ - ¢¨âáï ¢ ᮮ⢥âá⢨¥ ¤¢¨¦¥¨¥ â®çª¨ ¯® ¥ª®â®à®© ªà¨¢®© ¢ ¯à®áâà á⢥ á®áâ®ï¨© (ä §®¢®¬ ¯à®áâà á⢥). â® ¤ ¥â
¢®§¬®¦®áâì ¯®«ãç¨âì £¥®¬¥âà¨ç¥áªãî, |
â®ç¥¥ { ª¨¥¬ - |
â¨ç¥áªãî [12, 15, 79], ¨â¥à¯à¥â æ¨î ¯®¢¥¤¥¨ï á¨á⥬ë. |
|
ਠ§ ¤ ®¬ ç «ì®¬ á®áâ®ï¨¨ x0 |
¯®«ã稬 à¥è¥¨¥ |
x(t) ãà ¢¥¨ï (5.1). äãªæ¨¨ ®â t ¢ ¯à®æ¥áᥠ᢮¥£® ¤¢¨- ¦¥¨ï â®çª x ®¯¨áë¢ ¥â ¥ª®â®àãî ªà¨¢ãî ¢ ¯à®áâà á⢥ á®áâ®ï¨© X: ⠪ਢ ï §ë¢ ¥âáï ä §®¢®© âà ¥ªâ®à¨¥© , ¨«¨ ä §®¢®© ªà¨¢®© á¨á⥬ë (5.1), ᮮ⢥âáâ¢ãî饩 § ¤ ë¬ ç «ìë¬ ãá«®¢¨ï¬. ®áª®«ìªã ¯à¥¤áâ ¢«ï¥â ¨â¥à¥á à §- ¢¨â¨¥ ¯à®æ¥áá ¢® ¢à¥¬¥¨, ä §®¢®© âà ¥ªâ®à¨¨ 㪠§ë¢ - ¥âáï (áâ५ª®©) ¯à ¢«¥¨¥ ¤¢¨¦¥¨ï ¨§®¡à ¦ î饩 â®çª¨ ¯à¨ ¢®§à áâ ¨¨ ¢à¥¬¥¨ t:
§®¢ë¬ ¯®àâà¥â®¬ á¨áâ¥¬ë §ë¢ ¥âáï ᮢ®ªã¯®áâì ä - §®¢ëå âà ¥ªâ®à¨©, ¯®«ãç¥ëå ¯à¨ à §«¨çëå ç «ìëå
ãá«®¢¨ïå.
áᬮâਬ ®á®¢ë¥ ᢮©áâ¢ ä §®¢ëå âà ¥ªâ®à¨© ¨ ä - §®¢ëå ¯®àâà¥â®¢ á¨á⥬ 㪠§ ®£® ª« áá . ⨠᢮©á⢠᫥¤ãîâ ¨§ ®¡é¨å å à ªâ¥à¨á⨪ à¥è¥¨© ¤¨ää¥à¥æ¨ «ì- ëå ãà ¢¥¨© [12, 79].
«ï á¨á⥬ ¢¨¤ (5.1) ¢ë¯®«¥ë ãá«®¢¨ï áâ ¤ àâëå â¥- ®à¥¬ áãé¥á⢮¢ ¨ï ¨ ¥¤¨á⢥®á⨠à¥è¥¨ï. ஬¥ â®-
109

£®, ®¨ ¢ë¯®«¥ë ¨ ¤«ï ãà ¢¥¨© ¢ "®¡à ⮬" ¢à¥¬¥¨
= ;t: ⨠ãà ¢¥¨ï ¨¬¥îâ ¢¨¤ dx=d = ;Ax( ): âáî- ¤ á«¥¤ã¥â, çâ® à¥è¥¨ï ãà ¢¥¨ï (5.1) ®¯à¥¤¥«¥ë ¢ ®¡« - á⨠t 2 (;1 1): ¢®©á⢮ áâ 樮 à®á⨠á¨áâ¥¬ë ¯à¨¢®¤¨â ª ⮬ã, çâ® ¯à¨ ¯®áâ஥¨¨ ä §®¢ëå âà ¥ªâ®à¨© ç «ìë© ¬®¬¥â ¥ áãé¥á⢥ { âà ¥ªâ®à¨¨, ¯à®å®¤ï騥 ç¥à¥§ ¥ª®- â®àãî â®çªã x0 ¢ à §«¨çë¥ ¬®¬¥âë ¢à¥¬¥¨ t1 t2 ¯à¥¤áâ - ¢«ïîâ ᮡ®© ®¤ã âà ¥ªâ®à¨î.
®í⮬ã:
¥à¥§ ª ¦¤ãî â®çªã ¯à®áâà á⢠á®áâ®ï¨© ¯à®å®- ¤¨â ¥ª®â®à ï ä §®¢ ï âà ¥ªâ®à¨ï. «¥¤®¢ ⥫ì®, ä §®¢ë© ¯®àâà¥â á¨áâ¥¬ë ¬®¦¥â ¡ëâì § ¯®«¥ ä §®¢ë¬¨ âà ¥ªâ®à¨- ﬨ ᪮«ì 㣮¤® ¯«®â®.
¨ª ª ï ä §®¢ ï âà ¥ªâ®à¨ï ¥ ¨¬¥¥â â®ç¥ª à §¢¥â¢«¥- ¨ï, â.¥. ® ¥ ¬®¦¥â à ᯠ¤ âìáï ¤à㣨¥ âà ¥ªâ®à¨¨.
¨ª ª¨¥ à §«¨çë¥ âà ¥ªâ®à¨¨ ¥ ¬®£ãâ ¨¬¥âì â®ç¥ª ¯¥à¥á¥ç¥¨ï. ⮠᢮©á⢮ á«¥¤ã¥â ¨§ ¥¤¨á⢥®á⨠à¥- 襨ï ãà ¢¥¨© ¢ ®¡à ⮬ ¢à¥¬¥¨. ®í⮬㠤«ï á¨á⥬ 㪠§ ®£® ¢¨¤ ⥪ã饥 á®áâ®ï¨¥ ®¤®§ ç® ®¯à¥¤¥«ï¥â ª ª ¡ã¤ã饥, â ª ¨ ¯à®è«®¥ à §¢¨â¨¥ ¯à®æ¥áá .
ª¨¬ ®¡à §®¬, à §«¨çë¥ ä §®¢ë¥ âà ¥ªâ®à¨¨ ¥ ¬®£ãâ ¯¥à¥á¥ª âìáï. ᫨ ã ¨å ¥áâì å®âï ¡ë ®¤ ®¡é ï â®çª , â® â ª¨¥ âà ¥ªâ®à¨¨ ¯à¥¤áâ ¢«ïîâ ᮡ®© ãç á⪨ ¥ª®â®à®© ®¤- ®© "¡®«¥¥ ¯®«®©" âà ¥ªâ®à¨¨, ¯®áâ஥®© ¤«ï ¡®«¥¥ ¯à®- â殮®£® ¢à¥¬¥®£® ¨â¥à¢ « . 1 ®à®âª® £®¢®àï, âà ¥ª- â®à¨¨ «¨¡® ¥ ¯¥à¥á¥ª îâáï, «¨¡® ᮢ¯ ¤ îâ (á â®ç®áâìî ¤® ¯à®¤®«¦¥¨ï), ¨«¨, ¤à㣨¬¨ á«®¢ ¬¨, ç¥à¥§ ª ¦¤ãî â®çªã
ä §®¢®£® ¯à®áâà á⢠¯à®å®¤¨â ®¤ |
¨ ⮫쪮 ®¤ ä §®¢ ï |
|||||
ªà¨¢ ï. |
|
|
|
|
||
|
|
¬®¯¥à¥á¥ª î騥áï âà ¥ªâ®à¨¨ ᮮ⢥âáâ¢ãîâ «¨¡® |
||||
¯®«®¦¥¨ï¬ (á®áâ®ï¨ï¬) à ¢®¢¥á¨ï á¨á⥬ë, ¨ ⮣¤ ®¨ |
||||||
¢ë஦¤ îâáï ¢ â®çªã, «¨¡® ¯¥à¨®¤¨ç¥áª¨¬ ¤¢¨¦¥¨ï¬. |
|
|||||
¯¥à¢®¬ á«ãç ¥ ¢ë¯®«¥®, çâ® ¤«ï ¢á¥å t |
2 R |
: x(t) = x |
£¤¥ |
|||
x |
|
|
|
|
|
|
|
2 X ¥ § ¢¨á¨â ®â t: ® ¢â®à®¬ á«ãç ¥ áãé¥áâ¢ã¥â ¥ª®- |
|||||
â®à®¥ § 票¥ T > 0 §ë¢ ¥¬®¥ ¯¥à¨®¤®¬ â ª®¥, çâ® ¯à¨ |
||||||
¯à®¨§¢®«ì®¬ t ¨¬¥îâ ¬¥áâ® à ¢¥á⢠|
x(t) = x(t +T ) ® ¯à¨ |
|||||
1 ᯮ«ì§ã¥âáï ¯®ï⨥ ¬ ªá¨¬ «ìëå (¥¯à®¤®«¦ ¥¬ëå) âà ¥ªâ®à¨©.®®â¢¥âáâ¢ãî騥 ¨¬ à¥è¥¨ï ¥ ¬®£ãâ ¡ëâì ¯à®¤®«¦¥ë ¨ ª ª®© ¡®«¥¥ è¨à®ª¨© ¨â¥à¢ «. «ï «¨¥©ëå á¨á⥬ ¨â¥à¢ «®¬ ®¯à¥¤¥«¥¨ï ¬ ªá¨¬ «ìëå âà ¥ªâ®à¨© ï¥âáï ¢áï ¢¥é¥á⢥ ï ¯àï¬ ï R.
110

jt1 ; t2j < T xi(t1) =6 xi(t2):
§®¢ ï âà ¥ªâ®à¨ï ¯¥à¨®¤¨ç¥áª®£® ¯à®æ¥áá ¯à¥¤áâ ¢«ï- ¥â ᮡ®© § ¬ªãâãî ªà¨¢ãî, §ë¢ ¥¬ãî § ¬ªã⮩ âà ¥ª- â®à¨¥©, ®à¡¨â®© ¨«¨ 横«®¬. ¬® à¥è¥¨¥ x(t) §ë¢ ¥âáï
¯¥à¨®¤¨ç¥áª¨¬ á ¯¥à¨®¤®¬ T:
5.2.®«¥ ä §®¢ëå ᪮à®á⥩. « áá¨ä¨ª æ¨ï ®á®¡ëå â®ç¥ª
5.2.1. ¥ªâ®à ä §®¢®© ᪮à®áâ¨
ª ®â¬¥ç¥® ¢ëè¥, à¥è¥¨î x(t) ᮮ⢥âáâ¢ã¥â ¤¢¨¦¥¨¥
â®çª¨ ¢ ¯à®áâà á⢥ |
X: ãáâì ¢ ¬®¬¥â ¢à¥¬¥¨ t0 â®çª |
|
¯à®å®¤¨â á®áâ®ï¨¥ x0 |
: ¯à¥¤¥«¨¬ ¢¥ªâ®àãî ᪮à®áâì â®ç- |
|
ª¨, ®¯¨áë¢ î饩 ¤ ®¥ à¥è¥¨¥, ¢ ¬®¬¥â ¥¥ ¯à®å®¦¤¥¨ï |
||
|
|
|
ç¥à¥§ ¯®«®¦¥¨¥ x0 : v = x(t) t=t0 |
: 票¥ ¢¥ªâ®à v §ë¢ - |
|
¥¬®£® ¢¥ªâ®à®¬ ä §®¢®© ᪮à®á⨠¨«¨ ¯à®áâ® ä §®¢®© ᪮à®- |
||
áâìî, § ¢¨á¨â ¥ ®â ¬®¬¥â t0 |
®â ª®®à¤¨ â â®çª¨, ç¥à¥§ |
|
ª®â®àãî ¢ ¤ ë© ¬®¬¥â ¯à®å®¤¨â âà ¥ªâ®à¨ï. â § ¢¨á¨- |
||
¬®áâì ¢ëà ¦ ¥âáï ãà ¢¥¨¥¬ (5.1), ¨§ ª®â®à®£® á«¥¤ã¥â, çâ® ¤«ï ¢â®®¬ëå «¨¥©ëå á¨á⥬ ¢¥ªâ®à ä §®¢®© ᪮à®á⨠¢ â®çª¥ x ®¯à¥¤¥«ï¥âáï à ¢¥á⢮¬
v(x) = Ax:
®áª®«ìªã ¢¥ªâ®à ä §®¢®© ᪮à®á⨠¯®ª §ë¢ ¥â ¢¥ªâ®àãî ᪮à®áâì à¥è¥¨ï x(t) â®, ¥á«¨ ¥£® ¨§®¡à §¨âì ®â®á¨â¥«ì® ¤ ®© â®çª¨, ¯®«ã稬 ¯à ¢«¥¨¥ ª á ⥫쮩 ª ä §®¢®© âà ¥ªâ®à¨¨, ¬®¤ã«ì ¢¥ªâ®à ᪮à®á⨠å à ªâ¥à¨§ã¥â ⥬¯ ¤¢¨¦¥¨ï â®çª¨ ¢¤®«ì âà ¥ªâ®à¨¨.
᫨ ¢ ª ¦¤®© â®çª¥ ¯à®áâà á⢠X ¨§®¡а §¨вм б®®в¢¥в- бв¢гойго ¥© д §®¢го бª®а®бвм, ¯®«гз¨¬ ¯®«¥ ä §®¢ëå ᪮- à®á⥩. ¬¥â¨¬, çâ® ¤«ï ¯®áâ஥¨ï ¯®«ï ä §®¢ëå ᪮à®á- ⥩ ¥â ¥®¡å®¤¨¬®á⨠à¥è âì ¤¨ää¥à¥æ¨ «ì®¥ ãà ¢¥¨¥ (5.1), â ª ª ª ¤«ï ª ¦¤®£® x § 票¥ v(x) = Ax: ®«¥ ä - §®¢ëå ᪮à®á⥩ ¤ ¥â £«ï¤®¥ ¨ 㤮¡®¥ ¯à¥¤áâ ¢«¥¨¥ ® ¯®¢¥¤¥¨¨ á¨á⥬ë, â ª ª ª ª á ⥫ìë¥ ª âà ¥ªâ®à¨ï¬ ¯®- §¢®«ïîâ ¤®áâ â®ç® â®ç® ¯à¥¤áâ ¢¨âì ¨ ¢¨¤ á ¬¨å âà ¥ª-
111
