Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4603 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Уфимский Государственный Авиационный Технический Университет
Предмет:
Теория автоматического управления
Файл:

Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления

.pdf
Скачиваний:
97
Добавлен:
02.05.2014
Размер:
2.56 Mб
Скачать
☆

­¨ï ¢¨¤

(1.3) á ¬ âà¨æ ¬¨

 

 

 

 

 

 

 

 

 

6

 

 

0

1

;

 

 

 

0

 

 

0

7

 

6

 

0

7

A=2

;k1m1;1

0

 

 

k2m1;1

 

0

3

B =2

 

0

3 :(1.19)

4

 

 

0

0

 

 

 

 

0

 

 

1

5

 

4

 

 

5

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

k

m;1

0

 

(k

1

+ k

)m;1

0

 

 

 

k m;1

 

 

 

1

2

 

 

 

 

2

 

2

 

 

 

 

2

2

 

᫨ ¢ë室 ¬¨ áç¨â âì ¯®«®¦¥­¨¥ ª®à¯ãá

y1(t) = h1 (t) ¨

à ááâ®ï­¨¥ ¬¥¦¤ã ®áìî ªà¥¯«¥­¨ï ª®«¥á ¨ ¯®¢¥àå­®áâìî

 

 

(t) ; h3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y1(t) = h2

(t) â® ¯®«ã稬 ¬ âà¨æë

 

 

 

 

 

 

 

 

 

 

1

0

0

0

D =

0

:

 

 

 

 

 

 

C = 0 0 1 0

;1

 

 

 

ਬ¥à 3. ¨­ ¬¨ª

âà¥åá⥯¥­­®£® £¨à®áª®¯ . á-

ᬮâਬ âà¥åá⥯¥­­®© £¨à®áª®¯ ¢ ª ठ­®¢®¬ ¯®¤¢¥á¥, ¯®¤- ¢¥à¦¥­­ë© ¢«¨ï­¨î ¢­¥è­¨å ¬®¬¥­â®¢ ®â­®á¨â¥«ì­® ª ठ- ­®¢ëå ®á¥©. ¡®§­ 稬: (t) (t) { ã£«ë ¯®¢®à®â ®á¨ à®â®à

£¨à®áª®¯ \ H { ¥£® ª¨­¥â¨ç¥áª¨© ¬®¬¥­â\ JB JC { ¬®¬¥­âë

¨­¥à樨\ MB(t) MC(t) { ¢­¥è­¨¥ ¬®¬¥­âë.

®£¤ «¨­¥ à¨-

§®¢ ­­ë¥ ãà ¢­¥­¨ï ¤¢¨¦¥­¨ï ®á¨ £¨à®áª®¯

(¢ ®âª«®­¥­¨ïå

®â­®á¨â¥«ì­® ­¥ª®â®à®£® ®¯®à­®£® 㣫 0) ¨¬¥îâ ¢¨¤ [91]

8

(t) = !C (t)

 

 

JC!C(t) =

; C!C (t) + H cos 0!B(t) + MC (t)

(1.20)

>

_(t) =

!B (t)

 

 

 

;H cos 0! (t) ; B!B(t) + MB(t)

 

< JB!B(t) =

 

£¤¥ ¯ à ¬¥âàë C

B å à ªâ¥à¨§ãîâ ¢«¨ï­¨¥ ᨫ ¢ï§ª®£®

>

 

 

 

 

:

 

 

 

 

â७¨ï\ !B (t) !C (t) { 㣫®¢ë¥ ᪮à®á⨠¨§¬¥­¥­¨ï ­ ¯à ¢«¥-

­¨ï ®á¨ £¨à®áª®¯ .

¢¥¤¥¬ ¢¥ªâ®à á®áâ®ï­¨ï

 

x(t) = [ (t)

!C (t) (t) !B(t)]

T

¨ ¢¥ªâ®à ¢å®¤

 

 

 

u(t) = [MB(t) MC (t)]: ®£¤

ãà ¢­¥­¨ï á®áâ®ï­¨ï £¨à®áª®¯ ¬®£ãâ ¡ëâì § ¯¨á ­ë ¢ ¢¨¤¥ (1.3), £¤¥

6

0

;

1

0

;

0

7

6

0

0

7

A =2 0

 

; CJ;1

0

H cos 0J;1

3 B =2 J;1

0

3:(1.21)

4

0

 

0

0

 

1

5

4

0

0

5

 

0

 

H cos 0JB;1

0

 

BJB;1

 

 

0

JB;1

 

ª ¢¨¤­® ¨§ ¯à¨¢¥¤¥­­ëå ¯à¨¬¥à®¢, ­¥á¬®âàï ­ â® çâ®

¢¥ªâ®à á®áâ®ï­¨ï ¯à¨­ ¤«¥¦¨â ­¥ª®â®à®¬ã

¡áâà ªâ­®¬ã ¯à®-

бва ­бв¢г X ¥£® ª®¬¯®­¥­вл ¬®£г⠮⮦¤¥бв¢«пвмбп б з¨б«®- ¢л¬¨ §­ з¥­¨п¬¨ ª®­ªа¥в­ле д¨§¨з¥бª¨е ¯¥а¥¬¥­­ле, ¯а¥¤- бв ¢«¥­­ле ¢ ¢л¡а ­­®© б¨бв¥¬¥ ¥¤¨­¨ж.

32

1.4.4.¨äà®¢ë¥ ãáâனáâ¢

áᬮâਬ ⥯¥àì ¯à¨¬¥àë à §­®áâ­ëå ãà ¢­¥­¨© á®áâ®ï- ­¨ï (1.5). ª ®â¬¥ç¥­® ¢ëè¥, â ª¨¥ ãà ¢­¥­¥­¨ï ¨á¯®«ì§ã-

овбп ¯а¨ ®¯¨б ­¨¨ ¤¨­ ¬¨ª¨ б¨бв¥¬ ¤¨бªа¥в­®£® ¢а¥¬¥­¨, ª ª®в®ал¬ ®в­®бпвбп ¨ ж¨да®¢л¥ б¨бв¥¬л ®¡а ¡®вª¨ ¨­д®а¬ - ж¨¨ ¨ г¯а ¢«¥­¨п.

ਬ¥à 1. ¨áªà¥â­®¥ ¨­â¥£à¨à®¢ ­¨¥. à®æ¥áá ¢ë- ç¨á«¥­¨ï ¨­â¥£à « ®â ä㭪樨 ­¥¯à¥à뢭®£® ¢à¥¬¥­¨ ¢ ¤¨á- ªà¥â­ëå á¨á⥬ å ­ «®£¨ç¥­ á㬬¨à®¢ ­¨î ¢å®¤­®© ¯®á«¥-

¤®¢ ⥫쭮áâ¨. â® ¬®¦­® ¯à¥¤áâ ¢¨âì ४ãà७⭮© ä®à-

¬ã«®© x[k + 1] = x[k] + u[k] £¤¥ u[k] { §­ 祭¨ï ¢å®¤­®£® ¯à®-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P

 

 

 

 

æ¥áá , x[k] { ¢ëç¨á«¥­­®¥ §­ 祭¨¥ á㬬ë (x[k] =

k;1

]):

i=0 u[i

ਭ¨¬ ï § á®áâ®ï­¨¥ ¨ ¢ë室 á¨áâ¥¬ë §­ 祭¨ï x[k]

¯®«ã-

 

稬 ãà ¢­¥­¨ï á®áâ®ï­¨ï ¢ ä®à¬¥ (1.5), £¤¥ A = 1 B = 1 C =

1 D = 0:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

¬¥â¨¬, çâ® ¥á«¨ ¢ëç¨á«¨â¥«ì­®¥ ãáâனá⢮ ¤®áâ â®ç­®

 

 

¯à®¨§¢®¤¨â¥«ì­®, ¯à¨ ¢ëç¨á«¥­¨¨ y[k] ¬®¦¥â ãç¨âë¢ âìáï ¢

 

y[k] §­ 祭¨¥ u[k] ¢ â®â ¦¥ ¬®¬¥­â ¢à¥¬¥­¨

 

y

[k] =

k

 

u[i]

 

:

®£¤ ¢ (1.5) D = 1:

 

 

 

 

 

 

 

 

Pi=0

 

 

ਬ¥à 2.

¨ä஢ ï 䨫ìâà æ¨ï.

 

áᬮâਬ æ¨-

ä஢®© ­¥à¥ªãàᨢ­ë© 䨫ìâà ­¨¦­¨å ç áâ®â, ॠ«¨§ãî騩

 

¯à®æ¥áá ¢ëç¨á«¥­¨ï ᪮«ì§ï饣® á।­¥£®, ­ ¯à¨¬¥à, §

ç¥âë-

ॠ⠪â à ¡®âë:

y[k] =

1

P

k;1

u[i]: â®â

 

«£®à¨â¬ ¬®¦­®

 

 

 

 

i=k;4

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

¯à¥¤áâ ¢¨âì á ¯®¬®éìî £à㯯ë í«¥¬¥­â®¢ ¯ ¬ï⨠(¨«¨ "§ -

 

¤¥à¦ª¨"), ¯¥à¢ë© ¨§ ª®â®àëå ¢®á¯à¨­¨¬ ¥â §­ 祭¨¥ ¢å®¤-

 

­®£® ¯à®æ¥áá .

ª ¦¤®¬ á«¥¤ãî饬 è £¥ ¢ë¯®«­ï¥âáï

 

"ᤢ¨£" ᮤ¥à¦¨¬®£® í«¥¬¥­â®¢ ¯ ¬ï⨠®â ¯¥à¢®£® í«¥¬¥­-

 

â ª ¯®á«¥¤ãî騬. ª¨¬ ®¡à §®¬, ¯à¨å®¤¨¬ ª à §­®áâ­ë¬

 

ãà ¢­¥­¨ï¬:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

>

x1[k + 1] = u[k]

 

 

 

 

 

 

 

 

 

 

[k + 1] = x1

[k]

 

 

 

 

 

 

 

 

 

8 x2

 

 

 

 

 

 

 

 

 

>

x3

[k + 1] = x2

[k]

 

 

 

 

 

 

(1.22)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

:

 

[k + 1] = x3[k]

 

 

 

 

 

 

 

 

 

< x4

 

 

 

 

 

 

 

 

 

y[k] =

1

 

(x1[k] + x2[k] + x3[k] + x4

[k])

 

 

 

 

 

 

 

 

 

 

 

 

¢ १ã«ìâ ⥠祣® ¯®«ãç ¥¬ ãà ¢­¥­¨ï á®áâ®ï­¨ï (1.5) á ¬ -

33

âà¨æ ¬¨

 

 

 

 

 

 

 

 

 

 

 

6

0

0

0

0

7

6

1

7

 

 

 

0

0

1

0

0

 

 

 

A = 2

1 0

0 0

3

B = 2

0

3

C =

1

[1 1 1 1]:

0

1

0

0

0

 

4

5

4

5

4

 

 

 

 

 

 

 

 

 

áᬮâ७­ë© ¯à¨¬¥à ¯®ª §ë¢ ¥â, çâ® ãà ¢­¥­¨ï á®áâ®-

ï­¨ï ç áâ® ¯à¨¢®¤ïâ ª à §à¥¦¥­­ë¬ ¬ âà¨æ ¬, ª®â®àë¥ á®- ¤¥à¦ ⠮⭮á¨â¥«ì­® ¡®«ì讥 ç¨á«® ­ã«¥¢ëå í«¥¬¥­â®¢. ®- í⮬㠤«ï ¨á¯®«ì§®¢ ­¨ï ¬¥â®¤ ¯à®áâà ­á⢠á®áâ®ï­¨© æ¥- «¥á®®¡à §­® ¯à¨¡¥£ âì ª «£®à¨â¬ ¬ ¢ëç¨á«¥­¨©, ®à¨¥­â¨- ஢ ­­ë¬ ­ ¤¥©á⢨ï á â ª¨¬¨ ¬ âà¨æ ¬¨ [77], â ª¦¥ ¨á- ¯®«ì§®¢ âì á¯¥æ¨ «ì­ë¥ (ª ­®­¨ç¥áª¨¥) ä®à¬ë § ¯¨á¨ ãà ¢- ­¥­¨© á®áâ®ï­¨ï. ¥ª®â®àë¥ ¨§ â ª¨å ä®à¬ à áᬠâਢ îâáï ¢ £« ¢¥ 2. á. 67.

1.5.¥à¥¤ â®ç­ë¥ ä㭪樨 ¨ ¨å ®¯à¥¤¥«¥­¨¥ ¯® ãà ¢- ­¥­¨ï¬ á®áâ®ï­¨ï

1.5.1. ¥à¥¤ â®ç­ë¥ ä㭪樨 «¨­¥©­ëå á¨á⥬

áᬮâਬ «¨­¥©­ãî áâ 樮­ à­ãî á¨á⥬㠭¥¯à¥à뢭®£® ¢à¥¬¥­¨

x(t) = Ax(t) + Bu(t)

y(t) = Cx(t) + Du(t)

(1.23)

«¨¡® ¤¨áªà¥â­ãî «¨­¥©­ãî áâ 樮­ à­ãî á¨á⥬ã

 

x[k + 1] = Ax[k] + Bu[k]

 

y[k] = Cx[k] + Du[k]

(1.24)

£¤¥ x2Rn y 2Rl u2Rm:

 

 

 

 

¯à¥¤¥«¥­¨¥ [3, 47, 66]. ëà ¦¥­¨¥

 

 

 

;1

 

 

 

W( ) = C; In ; A

 

B + D

2 C

(1.25)

­ §ë¢ ¥âáï ¯¥à¥¤ â®ç­®© ä㭪樥© á¨á⥬ë (1.23) (¨«¨ (1.24))

®â ¢å®¤ u ª ¢ë室ã y:

2

 

 

 

 

¬¥â¨¬, çâ® W( ) ï¥âáï ¬ âà¨ç­®© ä㭪樥© à §¬¥-

àl m ®â ª®¬¯«¥ªá­®£® à£ã¬¥­â . «¨â¥à âãॠ¯® ⥮ਨ

ॣ㫨஢ ­¨ï ®¡ëç­® ¯à¨­ïâ® ¤«ï ­¥¯à¥à뢭ëå á¨á⥬ à- £ã¬¥­â ¯¥à¥¤ â®ç­®© ä㭪樨 ®¡®§­ ç âì ç¥à¥§ s ¨«¨ p, ¤«ï ¤¨áªà¥â­ëå á¨á⥬ { ç¥à¥§ z [15, 47, 66, 76, 95, 93].

34

¥а¥¤ в®з­л¥ дг­ªж¨¨ з бв® ¨б¯®«м§говбп ¢ а §«¨з­ле § ¤ з е ¨бб«¥¤®¢ ­¨п ¤¨­ ¬¨з¥бª¨е (¢ ¯¥а¢го ®з¥а¥¤м { «¨- ­¥©­ле ¨ бв ж¨®­ а­ле) б¨бв¥¬. а¨¬¥­¥­¨¥ нв¨е дг­ªж¨© ¤«п ¯®«гз¥­¨п з бв®в­ле е а ªв¥а¨бв¨ª ¡г¤¥в ¯®ª § ­® ¢ б«¥¤гой¥¬ ¯ а £а д¥. в®¡л б¤¥« вм ¤ ­­®¥ ®¯а¥¤¥«¥­¨¥ ¬¥­¥¥ д®а¬ «м­л¬ ¨ ¯®ª § вм, ª ª ¬®¦­® ¢¢¥бв¨ ¯¥а¥¤ в®з- ­л¥ дг­ªж¨¨ ¢ ¤аг£¨е б¨вг ж¨пе, ¨б¯®«м§г¥¬ ¤«п ¢л¢®¤ ¢л- а ¦¥­¨п (1.25) ¯à¥®¡à §®¢ ­¨¥ ¯« á 10 [15, 66, 76, 93, 94, 95].«ï í⮣® ¯à¨ ­ã«¥¢ëå ­ ç «ì­ëå ãá«®¢¨ïå x0 = 0 ¯¥à¥©-

 

 

 

 

 

 

 

x(t)

 

¤¥¬ ª ¨§®¡à ¦¥­¨ï¬ ¯® ¯« áã [66]: X (s) =

L

Y (s) =

 

y(t)

 

 

u(t) : ®£¤ ¯à¨ det(sIn

 

 

 

 

L

U(s) =

L

;

A) = 0 ¯®«ãç ¥¬

 

 

 

 

6

 

X (s) = (sIn ; A);1 BU(s) ¨ Y (s) = ;C (sIn ; A);1 B + D U(s):

ª¨¬ ®¡à §®¬, ¬ë ­ 諨 ¬ âà¨ç­ë© ¬­®¦¨â¥«ì, á¢ï§ë¢ î- 騩 ¨§®¡à ¦¥­¨ï ¯® ¯« á㠢室­®£® ¨ ¢ë室­®£® ¯à®æ¥á- ᮢ ¯à¨ ­ã«¥¢®¬ ­ ç «ì­®¬ á®áâ®ï­¨¨ { ¯¥à¥¤ â®ç­ãî äã­ª- æ¨î ¤ ­­®© á¨á⥬ë (1.25).

«ï ¤¨áªà¥â­ëå á¨á⥬ (1.24) ­ «®£¨ç­ë© १ã«ìâ â ¯®- «ãç ¥âáï á ¯®¬®éìî z-¯à¥®¡à §®¢ ­¨ï [76, 66].

«ï áâண® ॠ«¨§ã¥¬ëå á¨á⥬ ¯¥à¥¤ â®ç­ ï äã­ªæ¨ï ¨¬¥¥â ¡®«¥¥ ¯à®á⮩ ¢¨¤ W( ) = C; In ; A ;1B ª®â®àë© ®¡ëç­® ¨ ¡ã¤¥¬ ¨á¯®«ì§®¢ âì ¢ ¤ «ì­¥©è¥¬.

§¬¥à ¬ âà¨æë W( ) ®¯à¥¤¥«ï¥âáï à §¬¥à­®áâﬨ ¢å®- ¤ ¨ ¢ë室 á¨á⥬ë. «ï á¨á⥬ á ®¤­¨¬ ¢å®¤®¬ ¨ ®¤­¨¬ ¢ë室®¬, y(t) 2 R u(t) 2 R l = m = 1 ¨ W( ) áâ ­®¢¨âáï ®â- ­®è¥­¨¥¬ ¬­®£®ç«¥­®¢ ®â : W( ) = B(A( )): ®¡й¥¬ б«гз ¥ ¯®«гз ¥вбп ¬ ва¨ж , н«¥¬¥­в ¬¨ ª®в®а®© п¢«повбп ¯¥а¥¤ -

â®ç­ë¥ ä㭪樨 W ( ) = Bi j( ) i = 1 : : : l j = 1 : : : m

i j Ai j ( )

®â ª ¦¤®£® ¢å®¤ ui ª ª ¦¤®¬ã ¢ë室ã yi :

 

2

.

3

= 2

.

 

.. .

.

3 2

 

.

3 :

 

 

Y1( )

 

 

W1 1( )

: : :

W1 m( )

 

U1

( )

 

 

4 Yl ( )

5

4 Wl 1

( ) : : : Wl m( )

5 4 Um ( ) 5

10

 

 

 

§®¡à ¦¥­¨¥¬ ¯® ¯« áã X(s) ¢¥ªâ®à-ä㭪樨 x(t) ­ §ë¢ ¥âáï äã­ª-

 

 

 

 

 

 

 

 

 

 

1

 

 

æ¨ï ª®¬¯«¥ªá­®© ¯¥à¥¬¥­­®© s § ¤ ­­ ï ª ª L;x(t) = R0

 

e;stx(t)dt:

 

 

 

 

 

 

 

35

 

 

 

 

 

 

1.5.2. «£®à¨â¬ë ¢ëç¨á«¥­¨ï ¯¥à¥¤ â®ç­ëå ä㭪権

áâ ­®¢¨¬áï ­ ¢ëç¨á«¨â¥«ì­®© áâ®à®­¥ ¯®«ã祭¨ï W( ).¨¡®«ìèãî á«®¦­®áâì ¯à¥¤áâ ¢«ï¥â ¢ëç¨á«¥­¨¥ १®«ì¢¥­-

 

 

 

 

 

 

 

 

A

;1

¬ âà¨æë A: ® ¯à ¢¨«ã ®¡à 饭¨ï

âë R( ) = In;

 

¬ âà¨æ ¢ë¯®«­¥­®

 

 

 

 

 

 

 

 

 

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R( ) = adj In

; A

 

 

 

 

 

 

 

 

 

 

 

 

det( In

;

A)

 

 

 

 

 

 

 

 

 

 

 

 

;

 

 

 

£¤¥ ç¥à¥§ adj(

) ®¡®§­ 祭 ¬ âà¨æ

 

«£¥¡à ¨ç¥áª¨å ¤®¯®«-

­¥­¨© ª

 

 

 

 

 

 

T

¨«¨ ¯à¨á®¥¤¨­¥­­ ï (ª In ; A) ¬ âà¨æ

 

In ; A

 

[53]. ­ ¬¥­ ⥫ì í⮣® ¢ëà ¦¥­¨ï ¥áâì ᪠«ïà­ë© ¬­®£®-

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ç«¥­ á⥯¥­¨ n

det( In ; A) = A( ) = n + a1 n;1 + a2 n;2 +

+an . ­ ­ §ë¢ ¥âáï å à ªâ¥à¨áâ¨ç¥áª¨¬ ¬­®£®ç«¥­®¬ ¬ - âà¨æë A: ª¨¬ ®¡à §®¬, ¢á¥ ¯¥à¥¤ â®ç­ë¥ ä㭪樨 Wi j ( )

¢ëç¨á«¥­­ë¥ ¯® ä®à¬ã«¥ (1.25), ¨¬¥îâ (á â®ç­®áâìî ¤® ¢®§- ¬®¦­ëå ᮪à 饭¨©) ®¤¨­ ª®¢ë¥ §­ ¬¥­ ⥫¨ Ai j ( ) A( ):®í⮬ã å à ªâ¥à¨áâ¨ç¥áª¨© ¬­®£®ç«¥­ ¬ âà¨æë A ᮢ¯ ¤ -

¥в б® §­ ¬¥­ в¥«¥¬ ¯¥а¥¤ в®з­®© дг­ªж¨¨ б¨бв¥¬л. ¨¤ ¯¥- а¥е®¤­®£® ¯а®ж¥бб ¢ б¨бв¥¬¥, ¥¥ гбв®©з¨¢®бвм ®¯а¥¤¥«повбп ª®а­п¬¨ i ¤ ­­®£® ¬­®£®ç«¥­ . ­ 祭¨ï i ­ §ë¢ îâáï ᮡá⢥­­ë¬¨ ç¨á« ¬¨ ¬ âà¨æë A: ­®¦¥á⢮ ᮡá⢥­­ëå ç¨á¥« f ig ¨§¢¥áâ­® ª ª ᯥªâà ¤ ­­®© ¬ âà¨æë [53]. ®í⮬ã ãá«®¢¨¥ ᨬ¯â®â¨ç¥áª®© ãá⮩稢®á⨠á¨á⥬ë (1.23) ¬®¦- ­® áä®à¬ã«¨à®¢ âì, ª ª âॡ®¢ ­¨¥ ⮣®, ç⮡ë ᯥªâà ¬ - âà¨æë A 楫¨ª®¬ à ᯮ« £ «áï ¢ «¥¢®© ¯®«ã¯«®áª®á⨠ª®¬-

¯«¥ªá­®© ¯«®áª®á⨠C: «ï

ᨬ¯â®â¨ç¥áª®© ãá⮩稢®áâ¨

¤¨áªà¥â­ëå á¨á⥬ (1.24) ᯥªâà ¬ âà¨æë A ¤®«¦¥­ «¥¦ âì

¢­ãâਠ®ªà㦭®á⨠¥¤¨­¨ç­®£® à ¤¨ãá ¯«®áª®á⨠C á 業-

â஬ ¢ ­ ç «¥ ª®®à¤¨­ â.

R( ) ®á«®¦­ï¥âáï ⥬, çâ® å -

ëç¨á«¥­¨¥ १®«ì¢¥­âë

à ªâ¥à¨áâ¨ç¥áª ï ¬ âà¨æ

In ; A ­¥ ç¨á«®¢ ï, äã­ªæ¨-

®­ «ì­ ï { § ¢¨á¨â ®â ¯¥à¥¬¥­­®© : ®í⮬ã áâ ­¤ àâ­ë¥ «£®à¨â¬ë ®¡à 饭¨ï ¬ âà¨æ (­ ¯à¨¬¥à, «£®à¨â¬ ãáá ) §¤¥áì ­¥ ¯à¨¬¥­¨¬ë. «ï à¥è¥­¨ï í⮩ § ¤ ç¨ à §à ¡®â ­ àï¤ á¯¥æ¨ «ì­ëå «£®à¨â¬®¢: ¥¢¥àì¥{ ¤¤¥¥¢ , ­¨«¥¢áª®- £®, ãàì¥ [47, 94], ¤ î騥 å®à®è¨© १ã«ìâ ⠯ਠ­¥¢ë᮪®¬ ¯®à浪¥ á¨á⥬ë. «ï ¬ âà¨æ ¢ë᮪®© à §¬¥à­®á⨠¯à¨ ¢ë- ç¨á«¥­¨¨ ¯® í⨬ «£®à¨â¬ ¬ ¯à®¨á室¨â ¡ëáâ஥ ­ ª®¯«¥- ­¨¥ ®è¨¡®ª ®ªà㣫¥­¨ï, á¢ï§ ­­ëå á ®£à ­¨ç¥­­®áâìî à §-

36

à來®© á¥âª¨ . «ï ãáâà ­¥­¨ï í⮣® ¥­¨ï à §à - ¡®â ­ë ¡®«¥¥ ãáâ®©ç¨¢ë¥ ¢ëç¨á«¨â¥«ì­ë¥ «£®à¨â¬ë, ®á­®-

¢­­ë¥ ­ ¯à¨¢¥¤¥­¨¨ ¬ âà¨æ á ¯®¬®éìî í«¥¬¥­â à­ëå ¯à¥- ®¡à §®¢ ­¨© ª â ª ­ §ë¢ ¥¬®© ª ­®­¨ç¥áª®© ä®à¬¥ ¥áᥭ- ¡¥à£ [1, 100]. 11

ਠ"àãç­®¬" ¢ëç¨á«¥­¨¨ ¯¥à¥¤ â®ç­®© ä㭪樨 ®ª §ë-

¢¥âáï ¡®«¥¥ 㤮¡­®© § ¯¨áì ãà ¢­¥­¨© á®áâ®ï­¨ï ¢ ®¯¥à - â®à­®© ä®à¬¥ [66] á ¯®á«¥¤ãî騬 ®¯à¥¤¥«¥­¨¥¬ ¢ë室­®© ¯¥à¥¬¥­­®© ç¥à¥§ à¥è¥­¨¥ á¨á⥬ «¨­¥©­ëå «£¥¡à ¨ç¥áª¨å

ãà ¢­¥­¨©. áᬮâਬ íâ®â ¬¥â®¤ ¡®«¥¥ ¯®¤à®¡­®.

¥à¥¯¨è¥¬ ¢ëà ¦¥­¨¥ ¤«ï ¯¥à¥¤ â®ç­®© ä㭪樨 ¢ ¢¨¤¥

 

;

 

 

 

 

W( ) = CWx ( )+D £¤¥ Wx( ) =

 

In

;

A ;1B: ( ¬¥â¨¬, çâ®

 

 

 

 

 

Wx ( ) ¥áâì n m-¬ âà¨ç­ ï ¯¥à¥¤ â®ç­ ï äã­ªæ¨ï ª ¢¥ªâ®àã

á®áâ®ï­¨ï á¨á⥬ë). ।áâ ¢¨¬ Wx ( ) ¨ B ¢ ¢¨¤¥

Wx( ) =

[w1( ) w2( ) : : : wm( )] B = [b1 b2 : : : bm] £¤¥

wj ( ) bj

j = 1 2 ::: m { á⮫¡æë 㪠§ ­­ëå ¬ âà¨æ Wx ( ) ¨ B: «ï

wj ( ), ®ç¥¢¨¤­®, ¯®«ãç ¥¬ ãà ¢­¥­¨ï

 

 

 

( In ; A)wj( ) = bj

j = 1 2 ::: m

(1.26)

ª ¦¤®¥ ¨§ ª®â®àëå ï¥âáï á¨á⥬®© n «¨­¥©­ëå ãà ¢­¥- ­¨© ®â­®á¨â¥«ì­® n ­¥¨§¢¥áâ­ëå ª®¬¯®­¥­â ¢¥ªâ®à-ä㭪権 wj ( ) = [w1j ( ) w2j( ) : : : wmj ( )]T . 室ï à¥è¥­¨ï (1.26) ¯® ä®à¬ã« ¬ à ¬¥à [3, 53, 66], ¯®«ã稬

wij ( ) =

ij( )

i = 1 2 : : : n j = 1 2 ::: m

(1.27)

( )

£¤¥ ( ) = det( In ; A) ¥áâì £« ¢­ë© ®¯à¥¤¥«¨â¥«ì á¨á⥬ë (1.27), ᮢ¯ ¤ î騩 á å à ªâ¥à¨áâ¨ç¥áª¨¬ ¬­®£®ç«¥­®¬ ¬ -

âà¨æë A,

ij ( ) ¥áâì ®¯à¥¤¥«¨â¥«¨, ¯®«ã祭­ë¥ § ¬¥­®© i-£®

á⮫¡æ å à ªâ¥à¨áâ¨ç¥áª®© ¬ âà¨æë In ; A ­

á⮫¡¥æ bj:

©¤ï ¢á¥ ®¯à¥¤¥«¨â¥«¨, ¯®«ã稬 ¬ âà¨ç­ãî ¯¥à¥¤ â®ç­ãî

äã­ªæ¨î

Wx ( ) ª á®áâ®ï­¨î á¨á⥬ë. ®á«¥ 㬭®¦¥­¨ï ­

¬ âà¨æã C ¨ á㬬¨à®¢ ­¨ï ¯®«ã祭­®£® ¢ëà ¦¥­¨ï á ¬ âà¨-

楩 D ­ 室¨¬ ¨áª®¬ãî ¯¥à¥¤ â®ç­ãî äã­ªæ¨î.

 

­­ë© ¯à¨¥¬ ¢ëç¨á«¥­¨© 㤮¡¥­ ¨ ¤«ï ãà ¢­¥­¨© ¡®«¥¥

®¡é¥£® ¢¨¤ , ­ ¯à¨¬¥à

 

 

A0x(t) = A1x(t) + B1u(t)

(1.28)

11 âà¨æ A ¯®à浪 n ¨¬¥¥â ¢¥àå­îî ª ­®­¨ç¥áªãî ä®à¬ã ¥áᥭ¡¥à£ , ¥á«¨ ¥¥ í«¥¬¥­âë aij 㤮¢«¥â¢®àïîâ ãá«®¢¨î aij = 0 ¤«ï i ; j 2 (i j = 1 2 : : : n).

37

£¤¥ A0

;

n n-¬ âà¨æ , detA0 = 0: ਠ¯¥à¥å®¤¥ ª áâ ­¤ àâ­®¬ã

 

;61

 

;1

B1: ਠ¢ëç¨á«¥­¨¨

¢¨¤ã (1.23) ¯®«ãç ¥¬ A = A0

A1 B = A0

¯¥à¥¤ â®ç­®© ä㭪樨 ¬®¦­® í⮣® ­¥ ¤¥« âì,

áà §ã à¥-

è âì ãà ¢­¥­¨ï

 

 

 

 

 

 

( A0 ; A1 )wj ( ) = bj

j = 1 2 ::: m:

(1.29)

« ¢­ë© ®¯à¥¤¥«¨â¥«ì á¨á⥬ë (1.29) ( ) = det( A0 ; A1) ¡ã¤¥â (á â®ç­®áâìî ¤® ¯®áâ®ï­­®£® ¬­®¦¨â¥«ï) ᮢ¯ ¤ âì á

åà ªâ¥à¨áâ¨ç¥áª¨¬ ¬­®£®ç«¥­®¬ ¬ âà¨æë A:

áᬮâਬ ­¥ª®â®àë¥ ¯à¨¬¥àë.

1.5.3. ਬ¥àë ¯¥à¥å®¤ ª ¯¥à¥¤ â®ç­ë¬ äã­ªæ¨ï¬ ®â ãà - ¢­¥­¨© á®áâ®ï­¨ï

ਬ¥à 1. «¥ªâà¨ç¥áª¨¥ 楯¨. ¥à­¥¬áï ª à áᬮâ७- ­ë¬ ¢ ¯. 1.4.1. á. 25, ãà ¢­¥­¨ï¬ RLC-楯¥©. ¥¯®á।- á⢥­­ë¬ ¢ëç¨á«¥­¨¥¬ ¯®«ãç ¥¬, çâ® ãà ¢­¥­¨ï¬ (1.12) ¯à¨

y(t) = x(t) (¢ë室 { ­ ¯à殮­¨¥ ­

¥¬ª®áâ¨) ᮮ⢥âáâ¢ã¥â

¯¥à¥¤ â®ç­ ï äã­ªæ¨ï W(s) =

 

s +

 

1

 

 

;1

 

1

 

=

 

1

 

: ­-

 

 

T

 

 

 

T

T s + 1

­ ï 楯ì ï¥âáï

 

 

 

 

 

 

 

 

 

 

 

 

 

 

¯¥à¨®¤¨ç¥áª¨¬ §¢¥­®¬ ¯¥à¢®£® ¯®à浪

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

¢ë室®¬ á¨-

[15, 76] ( ¨«¨ 䨫ìâ஬ ­¨¦­¨å ç áâ®â). ®£¤

á⥬ë ï¥âáï ­ ¯à殮­¨¥ uR (t) ­

§ ¦¨¬ å १¨áâ®à , ¯®-

 

 

 

 

 

T s

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

«ãç ¥¬ W(s) = T s

+ 1 { ¤¨ää¥à¥­æ¨àãî饥 §¢¥­® á § ¬¥¤-

«¥­¨¥¬.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

«ï ª®«¥¡ ⥫쭮£® ª®­âãà

(1.13),

á.

26, á¨á⥬

(1.26)

¨¬¥¥â ¢¨¤

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(s + RL;1)w1(s) + L;1w2(s) = L;1

 

 

 

 

 

 

 

 

;C;1w1(s) + sw2(s) = 0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

®âªã¤

(Ls + R)w1

(s) + w2(s) = 1

 

 

 

(1.30)

 

 

 

;w1 (s) + sCw2(s) = 0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

£¤¥ s

2 C

 

w1(s) w2 (s) { ¯¥à¥¤ â®ç­ë¥ ä㭪樨 ª ¯¥à¥¬¥­­­ë¬

x1 x2

 

 

 

 

 

 

 

 

2

+ RCs

+ 1 1(s) = Cs

: § (1.30) ­ 室¨¬ (s) = LCs

 

2(s) = 1 ¯®í⮬ã

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Cs

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

w1(s) = LCs2

+ RCs + 1

w2 (s) = LCs2

+ RCs + 1:

ç¨âë¢ ï ãà ¢­¥­¨¥ ¢ë室 ¢ (1.13), ¯®«ãç ¥¬ ¯¥à¥¤ â®ç- ­ãî äã­ªæ¨î

W(s) = ;Rw1(s);w2 (s)+1 = ;RCs ; RL ;2 1 + LCs2 + RCs + 1 = LCs + RCs + 1

38

 

 

Ks2

 

 

 

 

R

 

 

C

 

 

 

 

2

 

=

T 2s2

+ 2 T s + 1

£¤¥ T = pLC K = LC = T

= 2 q L

: ­-

­ ï ¯¥à¥¤ â®ç­ ï äã­ªæ¨ï ᮮ⢥âáâ¢ã¥â ª®¬¡¨­ 樨 ¤¢®©-

­®£® ¤¨ää¥à¥­æ¨àãî饣® §¢¥­ ¨ ª®«¥¡ ⥫쭮£® (¯à¨ < 1) ¨«¨ ¯¥à¨®¤¨ç¥áª®£® ¢â®à®£® ¯®à浪 [15, 76] (¯à¨ 1) §¢¥- ­ì¥¢. ª ç¥á⢥ ç áâ®â­®-¨§¡¨à ⥫쭮£® 䨫ìâà ®­® ï- ¥âáï 䨫ìâ஬ ¢¥àå­¨å ç áâ®â ( -䨫ìâ஬).

⬥⨬, çâ® ¢ à áᬮâ७­ëå á«ãç ïå à §¬¥à­®áâì ¯à®- áâà ­á⢠á®áâ®ï­¨© á¨á⥬ë ᮢ¯ ¤ ¥â á® á⥯¥­ìî §­ ¬¥- ­ â¥«ï ¯¥à¥¤ â®ç­®© ä㭪樨. ஬¥ ⮣®, ã áâண® ॠ«¨§ã- ¥¬ëå á¨á⥬ á⥯¥­ì ç¨á«¨â¥«ï ¯¥à¥¤ â®ç­®© ä㭪樨 ­¨¦¥ á⥯¥­¨ §­ ¬¥­ ⥫ï. ਠD =6 0 ®­¨ ᮢ¯ ¤ îâ. ­­ ï § ¢¨á¨¬®áâì ¨¬¥¥â ®¡é¨© å à ªâ¥à ¨ ¡ã¤¥â ­ ¡«î¤ âìáï ¢

¤«ì­¥©è¥¬.

¯®á«¥¤ãîé¨å ¯à¨¬¥à å ¤«ï ¢ëç¨á«¥­¨ï ¯¥à¥¤ â®ç­ëå ä㭪権 ¡ã¤¥¬ ¨á¯®«ì§®¢ âì ᮮ⭮襭¨ï (1.28), (1.29).

ਬ¥à 2. ¢¨£ â¥«ì ¯®áâ®ï­­®£® ⮪ . áᬮâਬ ¬®¤¥«ì ¤¢¨£ â¥«ï ¯®áâ®ï­­®£® ⮪ (1.14), á.26. à ¢­¥­¨ï (1.29) ¯à¨­¨¬ îâ ¢¨¤

 

8

sw e(s) ; w! e(s) = 0

 

(Ls + R)wi e(s) + Cew! e(s) = 1

 

<

;CM wi e(s) + J w! e (s) = 0

 

:sw M (s)

; w! M (s) = 0

â ª¦¥

8

(Ls + R)wi M (s) + Cew! M (s) = 0

 

<

;CM wi M (s) + Jw! M (s) = ;1:

¤¥áì wj k(s) j

:

i !

k

2 f

e M

g

п¢«повбп ¯¥а¥¤ в®з­л-

 

2 f

 

g

 

 

 

¬¨ äã­ªæ¨ï¬¨ ®â ¢å®¤®¢ e(t) M(t) ª ¯¥à¥¬¥­­ë¬ á®áâ®ï­¨ï

(t) i(t) !(t): ®áª®«ìªã ¢ ¤ ­­®¬ ¯à¨¬¥à¥ ¢ë室®¬ áç¨â - ¥âáï ¢¥ªâ®à [ (t) i(t)]T ­ á ¡ã¤ãâ ¨­â¥à¥á®¢ âì ç¥âëॠ¯¥- । â®ç­ë¥ ä㭪樨: w e(s) w M (s) wi e (s) wi M (s): ©- ¤¥¬ ®¯à¥¤¥«¨â¥«¨ (s) = s(JLs2 + JRs + CeCM ) (s) e = CM(s) M = ;(Ls + R) (s)i e = Js2 (s)i e = Ces ®âªã¤ ¯®«ã- 稬 ¬ âà¨ç­ãî ¯¥à¥¤ â®ç­ãî äã­ªæ¨î á¨á⥬ë (1.14):

 

 

 

CM

 

 

2;(Ls+R)

 

 

2

 

 

 

 

 

s(JLs

+JRs+CeCM )

 

s(JLs

+JRs+CeCM )

W(s)=2

 

 

Js

 

 

 

 

Ce

3 : (1.31)

4

 

J Ls2 +JRs+CeCM

 

 

J Ls2 +J Rs+CeCM

5

¬¥â¨¬, çâ® ¢ ¤ ­­®¬ ¯à¨¬¥à¥ á㬬

á⥯¥­¥© §­ ¬¥­ â¥-

«¥© ¯¥à¥¤ â®ç­ëå ä㭪権 (¤ ¦¥ á ãç¥â®¬ ᮪à 饭¨ï ­ã- 39

«¥© ¨ ¯®«îᮢ) à ¢­ ¤¥áïâ¨, ¢ â® ¢à¥¬ï ª ª á¨á⥬ ®¯¨- áë¢ ¥âáï ãà ¢­¥­¨ï¬¨ á®áâ®ï­¨ï âà¥â쥣® ¯®à浪 . ®¦­® ᤥ« âì ¢ë¢®¤, çâ® ¤«ï ¬­®£®á¢ï§­ëå á¨á⥬ (á¨á⥬, ¨¬¥î- é¨å ­¥áª®«ìª® ¢å®¤®¢ ¨ ¢ë室®¢) ãà ¢­¥­¨ï á®áâ®ï­¨ï ¬®£ã⠯ਢ¥á⨠ª ॠ«¨§ 樨 ¬¥­ì襣® ¯®à浪 , 祬 ᮢ®ªã¯­®áâì ¯¥à¥¤ â®ç­ëå ä㭪権. 12

ª ¢¨¤­® ¨§ ¯®«ã祭­ëå ¢ëà ¦¥­¨©, à áᬠâਢ ¥¬ë© ®¡ê¥ªâ ¤¥¬®­áâà¨àã¥â à §­®®¡à §­®¥ ¯®¢¥¤¥­¨¥ ¢ § ¢¨á¨¬®- á⨠®â ⮣®, ­ ª ª®© ¢å®¤ ¯®áâ㯠¥â ¢®§¤¥©á⢨¥ ¨ ª ª ï ¢ë- 室­ ï ¯¥à¥¬¥­­ ï ®¯à¥¤¥«ï¥âáï. ® 㣫㠢à 饭¨ï à®â®à ¤¢¨£ ⥫ì ï¥âáï §¢¥­®¬ ¨­â¥£à¨àãî饣® ⨯ ¢ á®ç¥â - ­¨¨ á ¯¥à¨®¤¨ç¥áª¨¬ §¢¥­®¬ ¢â®à®£® ¯®à浪 ¨«¨ á ª®«¥¡ - ⥫ì­ë¬ §¢¥­®¬ { ¢ § ¢¨á¨¬®á⨠®â ᮮ⭮襭¨ï ¯ à ¬¥â஢.᫨ JR2 4LCeCM â® ¯à®æ¥áá ¨¬¥¥â ¯¥à¨®¤¨ç¥áª¨©, ¨­ - ç¥ { ª®«¥¡ ⥫ì­ë©, å à ªâ¥à. ® 类୮¬ã ⮪㠤¢¨£ ⥫ì ï¥âáï §¢¥­®¬ ¤¨ää¥à¥­æ¨àãî饣® ⨯ (®â ­ ¯à殮­¨ï

¨áâ®ç­¨ª ) «¨¡® ¯®§¨æ¨®­­ë¬ §¢¥­®¬ (®â ¬®¬¥­â ­ £à㧪¨).

 

­¥à樮­­®áâì ⮪®¢®© 楯¨ ¨¬¥¥â ⮦¥ ¯¥à¨®¤¨ç¥áª¨© «¨-

 

¡® ª®«¥¡ ⥫ì­ë© å à ªâ¥à. ª ç¥á⢥ ¨««îáâà 樨 ­

à¨á.

 

1.8 ¯à¨¢¥¤¥­ë £à 䨪¨ ¯¥à¥å®¤­ëå å à ªâ¥à¨á⨪ ¤«ï ¯¥à¥-

 

¤ â®ç­®© ä㭪樨 (1.31).

 

 

 

 

 

ਬ¥à 3. ¥â ⥫ì­ë¥

¯¯ à âë. ¡à ⨬áï ⥯¥àì

ª ãà ¢­¥­¨ï¬ ¤¢¨¦¥­¨ï «¥â ⥫ì­ëå ¯¯ à ⮢. áᬮâਬ

 

á­ ç «

㣫®¢®¥ ¤¢¨¦¥­¨¥ ¨áªãáá⢥­­®£® á¯ãâ­¨ª , ®¯¨á ­-

 

­®¥ ¢ ¯.

1.4.2. á. 27.

à ¢­¥­¨ï (1.15) ¢ ä®à¬¥ (1.29),

 

¨¬¥îâ ¢¨¤

 

 

 

 

 

 

 

 

 

sw (s) ; w! (s) = 0

 

(1.32)

 

 

Jxsw!(s) = 1:

 

 

 

âáî¤

¯®«ã稬 (s) = Jxs2 (s) = 1 W(s) =

K

K

= J;1

 

 

 

 

 

 

2

 

x

 

 

 

 

 

 

s

¤¢®©­®¥

 

â.¥. à áᬠâਢ ¥¬ ï á¨á⥬ ¯à¥¤áâ ¢«ï¥â ᮡ®©

 

¨­â¥£à¨àãî饥 §¢¥­®.

 

 

 

 

 

 

®«¥¥ á«®¦­®© § ¤ 祩 ï¥âáï ¯®«ã祭¨¥ ¯¥à¥¤ â®ç­ëå

 

ä㭪権 «¥â ⥫쭮£®

¯¯ à â

á. 28, § ¤ ­­®£® ãà ¢­¥­¨ï-

 

¬¨ (1.16) (¢ «¨­¥ ਧ®¢ ­­®¬ ¢¨¤¥ { ãà ¢­¥­¨ï¬¨ á®áâ®ï­¨ï

 

á ¬ âà¨æ ¬¨ (1.17)).

 

 

 

 

 

 

12 «¨â¥à âãॠ¢áâà¥ç îâáï á«¥¤ãî騥 ᮪à 饭¨ï:

{¯à¨ l = m = 1 á¨á⥬ ®â­®á¨âáï ª ¢¨¤ã SISO (single input { single output),

{¯à¨ l > 1 m > 1 { ª ¢¨¤ã MIMO (multi input { multi output).

®§¬®¦­ë, ᮮ⢥âá⢥­­®, ¢ ਠ­âë SIMO ¨ MISO.

40

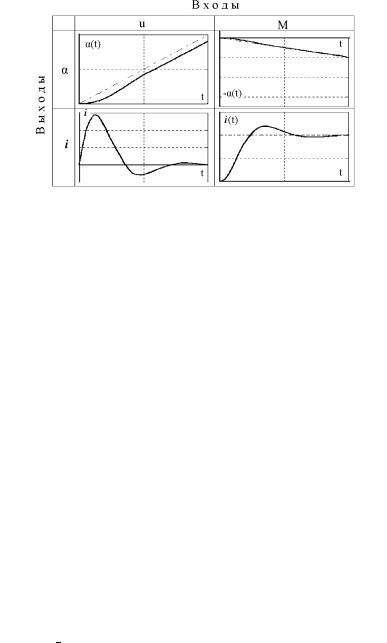
¨á. 1.8. ¥à¥å®¤­ë¥ å à ªâ¥à¨á⨪¨ ¤¢¨£ ⥫ï.

­­ ï á¨á⥬ ®¯¨áë¢ ¥âáï ¬ âà¨ç­®© ¯¥à¥¤ â®ç­®© äã-

­ªæ¨¥© è¥á⮣® ¯®à浪 . áᬮâਬ ã¯à®é¥­­ãî ¬®¤¥«ì ¯®­¨¦¥­­®£® ¯®à浪 , ¢ ª®â®à®© ­¥ ãç¨âë¢ îâáï ­¥ª®â®àë¥ ¯¥à¥¬¥­­ë¥ á®áâ®ï­¨ï, ¢å®¤ë ¨ ¢ë室ë á¨á⥬ë.

ª ¨§¢¥áâ­®, ¢ ¤¨­ ¬¨ª¥ ¬®¦­® ¢ë¤¥«¨âì á«¥¤ãî騥 ¯à®æ¥ááë, ®â«¨ç î騥áï ⥬¯®¬ (᪮à®áâìî ¯à®â¥ª ­¨ï) [19, 23, 98]:

{ ¨§¬¥­¥­¨¥ §¥¬­®© ᪮à®á⨠V (t)\

{ ¨§¬¥­¥­¨¥ ¯®«®¦¥­¨ï 業âà ¬ áá x(t) H(t)\

{ ¨§¬¥­¥­¨¥ 㣫®¢®£® ¯®«®¦¥­¨ï ª®®à¤¨­ â­ëå ®á¥© ®â­®á¨â¥«ì­® 業âà ¬ áá: (t) #(t) !z(t):

¨¡®«¥¥ ¡ëáâà® ¯à®â¥ª îâ ¯à®æ¥ááë ¨§¬¥­¥­¨ï 㣫®¢ëå ª®®à¤¨­ â, ¯®í⮬㠯ਠ¨áá«¥¤®¢ ­¨¨ íâ¨å ¯à®æ¥áᮢ ¬®¦­® (¯à¨¡«¨¦¥­­®) ¯à¥­¥¡à¥£ âì ¨§¬¥­¥­¨¥¬ ᪮à®á⨠¨ ¢ëá®âë ¯®«¥â . ¨¦¥ à áᬮâਬ ¬®¤¥«ì ¨§®«¨à®¢ ­­®£® 㣫®- ¢®£® ¤¢¨¦¥­¨ï, ª®â®à ï ¯®«ãç ¥âáï ¨áª«î祭¨¥¬ ãà ¢­¥­¨© ¤«ï V x H ¨§ (1.16) ¨ «¨­¥ ਧ 樨. ¯ã᪠ï ᨬ¢®« ¢ ®¡®§­ 祭¨ïå ®âª«®­¥­¨© ®â ®¯®à­®© âà ¥ªâ®à¨¨, § ¯¨è¥¬ «¨­¥ ਧ®¢ ­­ë¥ ãà ¢­¥­¨ï ¢ ¢¨¤¥ [23]

8

_(t) = ( a

+ a ) (t)

;

a #(t) + a ¢

(t)

 

; y

y

!z

y

 

y ¢

¢

(1.33)

!z(t) = amz (t) ; amz !z(t) ; amz #(t) ; amz ¢ (t)

:

 

 

 

 

 

 

 

 

 

< #(t) = !z(t):

 

 

 

 

 

 

 

ਠà áᬮâ७¨¨ 㣫®¢®£® ¤¢¨¦¥­¨ï ç áâ® ¬®¦­® ¯à¥­¥- ¡à¥£ âì (¢¢¨¤ã ¬ «®áâ¨) ª®íää¨æ¨¥­â®¬ ay å à ªâ¥à¨§ãî-

41

Соседние файлы в предмете Теория автоматического управления
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности