
Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления
.pdf
áᬮâਬ â ª¦¥ ª®¬¡¨¨à®¢ ë© § ª® áâ ¡¨«¨§ 樨, ¯à¨ ª®â®à®¬ ¢ ᨣ « ã¯à ¢«¥¨ï (¢ ¤ ®¬ á«ãç ¥ { ¢ ã¯à ¢«ïî- 騩 ¬®¬¥â) ¢¢®¤¨âáï â ª¦¥ ª®¬¯¥á¨àãî饥 ¢®§¤¥©á⢨¥ ¯®
¢®§¬ã饨î. ª ª ª ¢®§¬ãé î騩 ¬®¬¥â ¥¯®á।á⢥- ® ¨§¬¥à¥ ¡ëâì ¥ ¬®¦¥â, ¨á¯®«ì§ã¥¬ ¥£® ®æ¥ªã ^ ( ) ¯®«ã-
M t
ç¥ãî ¡«î¤ ⥫¥¬ (8.20). ®£¤ ª®¬¡¨¨à®¢ ë© § ª® ã¯à ¢«¥¨ï ¯à¨¨¬ ¥â ¢¨¤ 9
^ |
|
u(t) = ;k! !x(t) ; kmM(t): |
(9.23) |
ë¡®à ª®íää¨æ¨¥â k! ¢ë¯®«¨¬ ¨áå®¤ï ¨§ ãá«®¢¨ï ¡ëáâà®- ¤¥©áâ¢¨ï ¯à®æ¥áá áâ ¡¨«¨§ 樨 ¢ § ¬ªã⮬ ª®âãà¥. ®®â- ¢¥âáâ¢ãî騩 í⮬㠪®âãàã å à ªâ¥à¨áâ¨ç¥áª¨© ¬®£®ç«¥ ¨¬¥¥â ¢¨¤ D(s) = s + kJ!x ®âªã¤ k! = ;Jxs1 £¤¥ s1 { § ¤ ®¥ § 票¥ ª®àï D(s): 祢¨¤®, çâ® ¤«ï ¤ ®© á¨áâ¥¬ë ª®- íää¨æ¨¥â ¯¥à¥¤ ç¨ ¯® ¢®§¬ã饨î km = 1: ¥§ã«ìâ âë ¬®- ¤¥«¨à®¢ ¨ï á¨á⥬ë áâ ¡¨«¨§ 樨 ¯à¨ 㪠§ ëå á. 195 ¯ à ¬¥âà å ¨ s1 = 0:2 á;1 ¯à¨¢¥¤¥ë à¨á. 9.2. ª ¢¨¤®
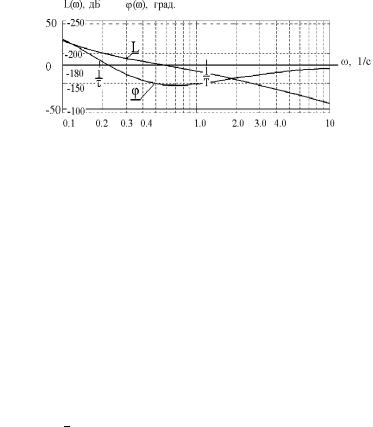
¨á. 9.2. à®æ¥ááë áâ ¡¨«¨§ 樨 .
¨§ à¨á㪠, ¯à¨ ¯à®¯®à樮 «ì®¬ § ª®¥ ã¯à ¢«¥¨ï ãáâ - ¢«¨¢ ¥âáï à ¢®ã᪮८¥ ¢à é ⥫쮥 ¤¢¨¦¥¨¥. á- ¯®«ì§®¢ ¨¥ ª®¬¡¨¨à®¢ ®£® § ª® ã¯à ¢«¥¨ï á ®æ¥ª®© ¨ ª®¬¯¥á 樥© ¢®§¬ãé¥¨ï ¢ ¤ ëå ãá«®¢¨ïå ¯à¨¢®¤¨â ª ᨬ¯â®â¨ç¥áª®¬ã áâ६«¥¨î ᪮à®á⨠ª ã«î. ãªâ¨à-
®© «¨¨¥© £à 䨪¥ u(t) ¯®ª § "¨¤¥ «ì ï" ª®¬¯¥á¨- àãîé ï á®áâ ¢«ïîé ï ¢ ã¯à ¢«ïî饬 ¢®§¤¥©á⢨¨, à ¢ ï
9 |
^ |
|
«¥¤ã¥â ãç¨âë¢ âì, çâ® ¯®áª®«ìªã ᨣ « M (t) ¢ëà ¡ âë¢ ¥âáï - |
¡«î¤ ⥫¥¬, ⮠ॣã«ïâ®à (¤¨ ¬¨ç¥áª¨© ª®¬¯¥á â®à) § ¤ ¥âáï ãà ¢¥- ¨ï¬¨ (8.20), (9.23).
212
;M (t): à¨á. 9.3 ¯à¨¢¥¤¥ ¤¨ £à ¬¬ ®¤¥ ( ) ¤«ï á¨á⥬ë áâ ¡¨«¨§ 樨 (8.17), (8.20), (9.23).
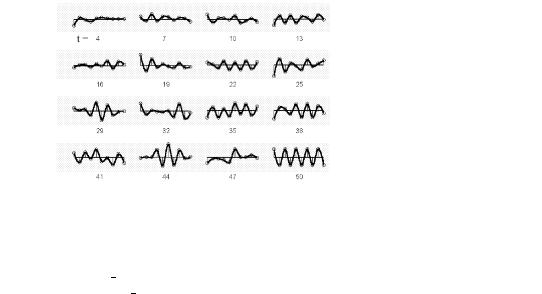
¨á. 9.3. ¨ £à ¬¬ë ®¤¥ á¨á⥬ë áâ ¡¨«¨§ 樨 á ॣã«ïâ®à®¬ (8.20), (9.23).
à 䨪¨ ¯®ª §ë¢ îâ «¨ç¨¥ ¤®áâ â®çëå § ¯ ᮢ ãá⮩- 稢®á⨠á¨á⥬ë (§ ¯ á ãá⮩稢®á⨠¯® ãᨫ¥¨î La = 12 ¤ , § ¯ á ãá⮩稢®á⨠¯® ä §¥ ' = 33o). ëç¨á«ïï ¯¥à¥- ¤ â®çãî äãªæ¨î ª®¬¯¥á â®à (8.20), (9.23) ®â ¢å®¤ !x
ª ã¯à ¢«¥¨î u ¯à¨ 㪠§ ëå § 票ïå ¯ à ¬¥â஢ ¯®«ã- 稬, çâ® à áᬮâà¥ë© § ª® ã¯à ¢«¥¨ï ¬®¦® ॠ«¨§®- ¢ âì §¢¥®¬ W(s) = k s2 + 2 s + 1 £¤¥ k = 1:13 á;2, T = 0:83
s2(T s + 1)
á, = 5:3 á. «ï ¢ë¯®«¥¨ï ¢ëç¨á«¥¨© ¨á¯®«ì§®¢ á«¥¤ã- î騩 äà £¬¥â ¯à®£à ¬¬ë ( ç «® ¯à®£à ¬¬ë ¯à¨¢¥¤¥®
á.196)
Km=1v Cá=[Kw Km 0]v Ac=A -B* áv Bc=Lv
{ä®à¬¨à®¢ ¨¥ ¬ âà¨æ ãà ¢¥¨© á®áâ®ï¨ï\
[num,den]=ss2tf(Ac,Bc,[Kw Km 0],0,1)v
{¢ëç¨á«¥¨¥ ¯¥à¥¤ â®ç®© äãªæ¨¨ ª®¬¯¥á â®à \ nf=num/Jv df=conv([1,0],den)
{¢ëç¨á«¥¨¥ ¯¥à¥¤ â®ç®© äãªæ¨¨ à §®¬ªã⮩ á¨áâ¥-
‘\ om=logspace(-1,1)v
[mag,ph]=bode(nf,df,om)v
{à áç¥â ç áâ®âëå å à ªâ¥à¨á⨪.
213

9.5.2. ®§¡ã¦¤¥¨¥ ª®«¥¡ ¨© ¢ 楯®çª¥ ®á樫«ïâ®à®¢
áᬮâਬ á¨á⥬ã, á®áâ®ïéãî ¨§ ¯®á«¥¤®¢ ⥫ì®á⨠®á- 樫«ïâ®à®¢ ( ¯à¨¬¥à, ¬ ï⨪®¢), ᮥ¤¨¥ëå ã¯à㣨¬¨
б¢п§п¬¨. ª п ¬®¤¥«м ¨б¯®«м§г¥вбп ¤«п ®¯¨б ¨п а §«¨з- ле д¨§¨з¥бª¨е ¨ ¬¥е ¨з¥бª¨е б¨бв¥¬ [52, 162]. ®вбгвбв¢¨¨ б¨« ва¥¨п ¨ ¯а¨ «¨¥©ле г¯аг£¨е ¤¥д®а¬ ж¨пе б¢п- §¥© (¢ ®¡« бв¨ ¤¥©бв¢¨п § ª® гª ) ж¥¯®зª N ¬ ï⨪®¢ ®¯¨áë¢ ¥âáï á¨á⥬®© ãà ¢¥¨©
8 |
|
|
|
; |
|
|
|
|
|
'1(t) + !2 sin'1 (t) = |
k '2(t) |
; '1 (t) + u(t) |
|
|
|
||
< |
|
2 |
: : : |
; |
|
; |
|
|
> |
'i(t) + !2 sin 'i(t) = |
k 'i+1(t) ; 2'i(t) + 'i+1(t) |
|
(9.24) |
||||
|
|
: : : |
|
(i = 2 3 : : : N |
1) |
|
||
: |
|
|
sin 'N (t) = k;'N;1(t) ; 'N (t) |
|
|
|
||
> |
'N (t) + ! |
|
|
|
|
|||
£¤¥ 'i(t) (i = |
1 2 : : : N) { ã£«ë ¯®¢®à®â ¬ ï⨪®¢\ |
u(t) |
||||||
{ ¢¥è¥¥ ã¯à ¢«ïî饥 ¢®§¤¥©á⢨¥, ¯à®¯®à樮 «ì®¥ ¬®- ¬¥âã, ¯à¨«®¦¥®¬ã ª ¯¥à¢®¬ã ¬ ï⨪ã\ ! k { ¯ à ¬¥âàë
á¨á⥬ë (! { ᮡá⢥ ï ç áâ®â ¬ «ëå ª®«¥¡ ¨© ¬ ïâ¨- ª®¢, k { ª®íää¨æ¨¥â ¦¥á⪮á⨠¯à㦨).
«¥¥ ¡ã¤¥¬ ¨á¯®«ì§®¢ âì «¨¥ ਧ®¢ ãî ¬®¤¥«ì, ¯à¥¤- ¯®« £ ï, çâ® ¬¯«¨â㤠ª®«¥¡ ¨© ¬ ï⨪®¢ ¥§ ç¨â¥«ì .ª ï ¬®¤¥«ì ¨¬¥¥â ¢¨¤
8 |
: : : |
|
2 |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
'1(t) + |
!2'1(t) = k '2 (t) ; '1(t) + u(t) |
|
|
|
|
|
|||||||||||||
'i(t) + ! 'i(t) = k 'i+1(t) |
; |
|
2'i(t) + 'i+1(t) |
|
|
(9.25) |
||||||||||||||
: : : |
|
|
|
|
|
(i = 2 3 : : : N |
|
1) |
|
|
|
|||||||||
> |
|
|
|
|
|
|
; |
|
2N |
|
|
|
|
; |
|
|
|
|
||
: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
< 'N (t) + !2'N (t) =;k 'N |
;1(t) |
; 'N |
(t) : |
|
|
|
||||||||||||||
¢¥¤¥¬ ¢¥ªâ®à á®áâ®ï¨ï x(t)2R |
|
|
x(t) = colf'1 '1 '2 '_2 : : : |
|||||||||||||||||
'N '_N g: áâ ¤ à⮩ ä®à¬¥ ãà ¢¥¨© á®áâ®ï¨ï |
|
|
|
|||||||||||||||||
x(t) = Ax(t) + Bu(t) ¬®¤¥«ì (9.25) § ¤ ¥âáï ¬ âà¨æ ¬¨ |
|
|
||||||||||||||||||
|
|
2 |
A1 |
|
A12 |
0 |
: : : 0 |
|
0 |
3 |
|
|
|
2 |
B1 |
3 |
|
|||
|
|
A12 |
|
A2 |
A12 |
: : : |
|
|
0 |
|
0 |
|
|
|
00 |
|
||||
A = |
0 A12 |
A2 |
... |
|
|
0 |
|
0 |
|
B |
= |
|
||||||||
|
. |
|
. . .. ... . |
|
. |
|
|
. |
|
|||||||||||
|
|
4 |
|
|
5 |
|
|
|
4 |
5 |
|
|||||||||
|
|
6 |
0 |
|
0 |
0 : : : A2 |
|
A12 |
7 |
|
|
|
6 |
0 |
7 |
|
||||
|
|
0 |
|
0 |
0 |
: : : A12 |
A1 |
|
|
|
0 |
|
||||||||
|
|
|
|
|
|
|
214 |
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
1 |
A2 |
0 |
1 |
A12 |
0 |
0 |
|
£¤¥ |
A1 = ;!2 ; k 0 |
= ;!2 ; 2k 0 |
= k 0 |
||||||
B1 = [ 0 1 ]T :
áᬮâਬ § ¤ çã ¢®§¡ã¦¤¥¨ï "¢®«ë" ª®«¥¡ ¨© § -
¤®© ¬¯«¨âã¤ë, ¯à¨ ª®â®àëå á®á¥¤¨¥ ¬ ï⨪¨ 室ïâáï ¢ ¯à®â¨¢®ä §¥. ਠí⮬ ®£à ¨ç¨¬áï âॡ®¢ ¨¥¬ ¯à¨-
¢¥¤¥¨ï ¨å ¢ íâ® á®áâ®ï¨¥ § § ¤ ®¥ ¢à¥¬ï ¨§ «î¡®£® - ç «ì®£® á®áâ®ï¨ï. «ï ¥¥ à¥è¥¨ï ¢®á¯®«ì§ã¥¬áï ¨§«®- ¦¥ë¬ ¢ ¯. 9.4. ¬¥â®¤®¬. ¯à ¢«¥¨¥ ¡ã¤¥¬ ¨áª âì ¢ ¢¨¤¥ ¯à®£à ¬¬®© äãªæ¨¨ ¢à¥¬¥¨ (9.13).
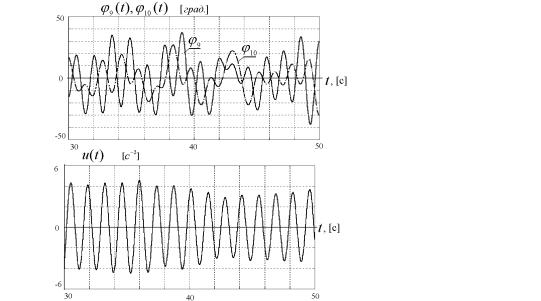
¨á. 9.4. ®« ª®«¥¡ ¨©.
¥§ã«ìâ âë à¥è¥¨ï § ¤ ç¨ ¤«ï N = 10 k = 5 á;2, ! = 0:4 á;1 'i(0) = 0 'i(0) = 0 (i = 1 2 : : : N), = 50 c, 'i( ) = (;1)i+1 30 £à ¤., 'i( ) = 0 ¯®ª § ë à¨á. 9.4, 9.5. ¯¥à¢®¬ ¨§®¡à ¦¥ë ¯®á«¥¤®¢ ⥫ì®á⨠¯®«®¦¥¨© ¬ ïâ¨- ª®¢ ¢ à §ë¥ ¬®¬¥âë ¢à¥¬¥¨ (®â¬¥ç¥ë æ¨äன ¢¨§ã). ¢â®à®¬ 9.5 ¯®ª § ë £à 䨪¨ 㣫®¢ ¯®¢®à®â '9(t) '10(t) ¨ ã¯à ¢«ïî饥 ¢®§¤¥©á⢨¥ u(t) ¯à®¬¥¦ã⪥ t 2 [30 50] á.¬¥â¨¬, çâ® ¢ ¤ ®¬ ¯à¨¬¥à¥ (ª ª ¨ ¢ ®¡é¥¬ á«ãç ¥) ¯à¨-
¢¥¤¥¨¥ á¨áâ¥¬ë ¢ § ¤ ®¥ á®áâ®ï¨¥ ¥ ®§ ç ¥â, ¢®®¡é¥ £®¢®àï, çâ® ® ®áâ ¥âáï ¢ í⮬ á®áâ®ï¨¨ ¨ ¤ «ìè¥ ¨«¨ ¡ã- ¤¥â ᮢ¥àè âì ¯à¥¤¯¨á ®¥ ¤¢¨¦¥¨¥. ᫨ ¨§ ¯®«ã祮£® á®áâ®ï¨ï x( ) ¯®áâநâì ã¯à ¢«¥¨¥, ¯¥à¥¢®¤ï饥 á¨á⥬㠢 íâ® ¦¥ á®áâ®ï¨¥ ª ¬®¬¥âã t = + ( > 0), â® ¯®«ã- 稬 ª®«¥¡ ¨ï á«®¦®© ä®à¬ë, ᨬ¬¥âà¨çë¥ ®â®á¨â¥«ì®
á¥à¥¤¨ë ¨â¥à¢ « [ + ]:
215
¨á. 9.5. £«ë ¯®¢®à®â ¬ ï⨪®¢ ¨ ã¯à ¢«¥¨¥.
«п ¢лз¨б«¥¨© ¨б¯®«м§г¥¬ б«¥¤гойго ¯а®£а ¬¬г.
MATLAB-¯à®£à ¬¬ ¬®¤¥«¨à®¢ ¨ï ¯à®æ¥áá ¢®§¡ã¦¤¥¨ï ¢®«ë ª®«¥¡ ¨©
k=5v om2=(0.2*2*pi)^2v |
N=10v |
{ ¢¢®¤ ¯ à ¬¥â஢ k ! ¨ ç¨á« |
¬ ï⨪®¢ N \ |
x0=zeros(2*N,1)v x1=zeros(2*N,1)v
{ ®¡ã«¥¨¥ ¬ áᨢ®¢ ç «ì®£® ¨ ª®¥ç®£® á®áâ®ï¨© t0=0v t1=50v
{ ¢¢®¤ t0 t1\ xmax=30/57.3v
{ ¢¢®¤ ¬¯«¨âã¤ë ª®«¥¡ ¨©\
A=zeros(2*N)v
{ ¢¢®¤ ã«¥¢ëå í«¥¬¥â®¢ ¬ âà¨æë A\
B=zeros(2*N,1)v B(2)=1v
{ ä®à¬¨à®¢ ¨¥ ¬ âà¨æë B\
A1=[0 1v -om2 0]v
216
{ ä®à¬¨à®¢ ¨¥ ¬ âà¨æë A1\ sig=1v
for in=1:N
{ ç «® 横« ä®à¬¨à®¢ ¨ï ¬ âà¨æë A ¨ ¢¥ªâ®à x1\ x1(2*(in-1)+1)=xmax*sigv
sig=-sigv
{ ä®à¬¨à®¢ ¨¥ ¯®á«¥¤®¢ ⥫ì®á⨠(;1)i\ for in1=1:N
l=2*(in1-1)+1v A(l:l+1,l:l+1)=A1v A(l+1,l)=A(l+1,l)-kv if ((in1>1)&(in1<N))
A(l+1,l)=A(l+1,l)-kv end
if in1<N A(l+1,l+2)=kv A(l+3,l)=kv
end end
end
{ ª®¥æ 横« ä®à¬¨à®¢ ¨ï ¬ âà¨æë A ¨ x1\
C=eye(2*N,2*N)v D=zeros(2*N,1)v
{ ä®à¬¨à®¢ ¨¥ ¬ âà¨æ C = I2 ¨ D = 0 ¤«ï ¬®¤¥«¨à®¢ ¨ï ¯® lsim (á¬. ਫ®¦¥¨¥ C. á. 431)\
Th=t1-t0v
{ ¢ëç¨á«¥¨¥ = t1 ; t0\ t=0:Th/1000:Thv Nt=length(t)v
w0=Bv u=zeros(size(t))v
{ ä®à¬¨à®¢ ¨¥ ç «ìëå ãá«®¢¨© w(0) = B ¨ ¢å®¤®£® ¢®§¤¥©á⢨ï u(t) 0 ¤«ï ¢ëç¨á«¥¨ï äãªæ¨¨ ¢¥á w(t)\
w=lsim(A,B,C,D,u,t,w0)v
{ ¢ëç¨á«¥¨¥ w(t)\
W=zeros(size(A))v
{ ç «ì®¥ ®¡ã«¥¨¥ ¬ áᨢ ¤«ï £à ¬¨ |
W( )\ |
for k=1:Nt |
|
W=W+w(k,:)'*w(k,:)v |
|
end |
|
W=W*Th/Nt |
|
{ ¢ëç¨á«¥¨¥ W( ) ¬¥â®¤®¬ ©«¥à \ |
|
217 |
|

c=inv(W)*(x1-expm(A*Th)*x0)v
{¢ëç¨á«¥¨¥ C ¯® ä®à¬ã«¥ (9.20)\ for k=1:Ntv u(k)=B'*expm(A'*(t1-t(k)))*cv end
{横« ä®à¬¨à®¢ ¨ï ¯à®£à ¬¬®£® ã¯à ¢«¥¨ï ¯® ä®à- ¬ã«¥ (9.13)\
[y,ti,x]=lsim(A,B,C,D,u,t,x0)v
{¬®¤¥«¨à®¢ ¨¥ á¨á⥬ë (¢ë¢®¤ £à 䨪®¢ ¢ë¯®«ï¥âáï áâ ¤ àâë¬ ®¡à §®¬).
9.6. ¤ ç¨ ¨ ã¯à ¦¥¨ï
1. ®ª § âì á¯à ¢¥¤«¨¢®áâì ⥮६ë à §¤¥«¥¨ï ¤«ï ¤¨ - ¬¨ç¥áª¨å ª®¬¯¥á â®à®¢, ¨á¯®«ì§ãîé¨å ¡«î¤ ⥫ì ã- ¥¡¥à£¥à .
2. «ï à áᬮâ८© ¢ ¯à¨¬¥à¥ á. 194 § ¤ ç¨ ¨¤¥- â¨ä¨ª 樨 ¢®§¬ã饨©, ¤¥©áâ¢ãîé¨å , ¯®«ãç¨âì «-
£®à¨â¬ ¤¨áªà¥â®£® ¡«î¤ â¥«ï ¯®«®£® ¯®à浪 , ¨¬¥îé¥- £® ¯®áâ®ïë¥ ¯ à ¬¥âàë ¨ ¨â¥à¢ « ª¢ ⮢ ¨ï T0, ª®â®- àë© ®æ¥¨¢ ¥â ¢®§¬ã饨¥ § ¨¬¥ì襥 ç¨á«® è £®¢ ¤¨á- ªà¥â®áâ¨. ᯮ«ì§®¢ âì ¯®«ãç¥ë¥ ®æ¥ª¨ ¯à¨ á¨â¥§¥ ¤¨áªà¥â®© áâ â¨ç¥áª®© á¨á⥬ë áâ ¡¨«¨§ 樨, ®¡¥á¯¥ç¨- ¢ î饩 ¨¬¥ì襥 ¢à¥¬ï ¯¥à¥å®¤®£® ¯à®æ¥áá .
3. ®«ãç¨âì [3] ãà ¢¥¨ï ¡«î¤ â¥«ï ¯¥à¢®£® ¯®à浪 ¤«ï ®¡ê¥ªâ , ¬®¤¥«ì ª®â®à®£® § ¤ ¬ âà¨æ ¬¨
|
2 |
1 |
1 |
1 |
3 |
|
2 |
0 |
3 |
|
0 |
0 |
1 |
|
|
A = |
0 |
1 |
0 |
B = |
1 |
C = |
: |
||||||||
|
0 |
1 |
1 |
|
1 |
|
1 |
0 |
0 |
|
|||||
|
4 |
|
|
|
5 |
|
4 |
|
5 |
|
|
|
|
|
|
4. ®«ãç¨âì ãà ¢¥¨ï ¡«î¤ â¥«ï ¯®«®£® ¯®à浪 |
|||||||||||||||
¤«ï 楯®çª¨ ¬ ï⨪®¢ 9.25, á. 214, ¯à¥¤¯®« £ ï, çâ® ¨§¬¥àï- |
||
¥âáï ⮫쪮 ®âª«®¥¨¥ i-£® ¬ ï⨪ (1 i N ): |
||
5. «ï á¨á⥬ë [3] |
|
|
x1 |
(t) = x1 |
(t) + x2(t) + u(t) |
x2 |
(t) = x1 |
(t) y(t) = x2(t) |
¯®«ãç¨âì ãà ¢¥¨ï ¤¨ ¬¨ç¥áª®£® ª®¬¯¥á â®à ¯¥à¢®£®
¯®à浪 , ®¡¥á¯¥ç¨¢ î饣® å à ªâ¥à¨áâ¨ç¥áª¨¥ ç¨á« § ¬ªã- ⮩ á¨á⥬ë, à ¢ë¥ s1 = ;3 s2 3 = ;2 |:
218

6. «ï ®¡ê¥ªâ ¢â®à®£® ¯®à浪 x(t) + x(t) = u(t) y(t) = x(t) + £¤¥ { ¯®áâ®ï®¥ ¥¨§¬¥à塞®¥ ¢®§¬ãé¥- ¨¥ [3], ¯®áâநâì ॣã«ïâ®à, ®¡¥á¯¥ç¨¢ î騩 ¯à¨ «î¡ëå
!0, y(t) ! 0 ¯à¨ t ! 1: ¯à¥¤¥«¨âì
¨¬¥ì訩 ¯®à冷ª ॣã«ïâ®à .
7.«ï § ¤ ç¨ 6 à áᬮâà¥âì [3] £ ମ¨ç¥áª®¥ ¢®§¬ã- 饨¥ (t) = 0 sin !t á ¨§¢¥á⮩ ç áâ®â®© !.
219

10.
10.1. ¡é¨¥ ᢥ¤¥¨ï ® ¥«¨¥©ëå á¨á⥬ å
¯à¥¤ë¤ãé¨å £« ¢ å ¨§ãç «¨áì «¨¥©ë¥ á¨á⥬ë. á- ᬮâਬ ¯®¤à®¡¥¥ § 票¥ í⮣® â¥à¬¨ . ¯à®é¥® ¬®¦® áç¨â âì, çâ® «¨¥©ë¥ á¨á⥬ë { íâ® â ª¨¥ á¨á⥬ë, ¤«ï ª®â®àëå á¯à ¢¥¤«¨¢ ¯à¨æ¨¯ á㯥௮§¨æ¨¨ { ॠªæ¨ï á¨- áâ¥¬ë «¨¥©ãî ª®¬¡¨ æ¨î (á㯥௮§¨æ¨î) ¢®§¤¥©á⢨© ᮢ¯ ¤ ¥â á â ª®© ¦¥ «¨¥©®© ª®¬¡¨ 樥© ॠªæ¨© ª - ¦¤®¥ ¢®§¤¥©á⢨¥ ¢ ®â¤¥«ì®áâ¨. 1 § í⮣® ®¡é¥£® ¯à¨æ¨- ¯ á«¥¤ã¥â, ¯à¨¬¥à, çâ® «¨¥©®¥ áâ â¨ç¥áª®¥ §¢¥® ¤®«¦- ® ®¯¨áë¢ âìáï «¨¥©®© (¯à®¯®à樮 «ì®©) § ¢¨á¨¬®áâìî y = Ku ¬¥¦¤ã ¢å®¤®¬ u(t) 2 Rm ¨ ¢ë室®¬ y(t) 2 Rl £¤¥ K { l m-¬ âà¨æ , § ¢¨áïé ï ®â t ¢ ¥áâ 樮 ஬ á«ãç ¥. ᫨ à áᬠâਢ ¥âáï ¤¨ ¬¨ç¥áª ï á¨á⥬ ¥¯à¥à뢮£® ¢à¥- ¬¥¨, â® ¢ «¨¥©®¬ ª®¥ç®¬¥à®¬ á«ãç ¥ ® ®¯¨áë¢ ¥â- áï «¨¥©ë¬¨ ¤¨ää¥à¥æ¨ «ì묨 ãà ¢¥¨ï¬¨, ¤¨áªà¥â ï á¨á⥬ { «¨¥©ë¬¨ à §®áâ묨 ãà ¢¥¨ï¬¨ ¨ â.¤.
¨бв¥¬л, ¤«п ª®в®але нв®в ¯а¨ж¨¯ ¥ ¢л¯®«п¥вбп, ®в®- бпвбп ª ¥«¨¥©ë¬. ¬¥в¨¬, зв® ¤ ®¥ ®¯а¥¤¥«¥¨¥ ®б¨в "¥£ в¨¢л©" е а ªв¥а ¢ ⮬ б¬лб«¥, зв® ®® гª §л¢ ¥в б¢®©бв¢®, ª®в®а®¥ г ®¯а¥¤¥«п¥¬ле б¨бв¥¬ ®вбгвбв¢г¥в. а - ¢¨«м¥¥ бª § вм, зв® б¢®©бв¢® «¨¥©®бв¨ ¢л¤¥«п¥в ª« бб «¨- ¥©ле б¨бв¥¬ ¨§ ¢б¥е (¢®®¡й¥ £®¢®ап, { ¥«¨¥©ле) б¨бв¥¬,¤ ª® ¨ ¢ в¥а¬¨®«®£¨з¥бª®¬, ¨ ¢ ¬¥в®¤¨з¥бª®¬ ®в®и¥¨¨ 㤮¡¥¥ бз¨в вм, зв® «¨¥©л¥ ¨ ¥«¨¥©л¥ б¨бв¥¬л ®в®- бпвбп ª а §л¬ ª« бб ¬.
⬥⨬, çâ® ¥á«¨ ¢ á®áâ ¢ á¨áâ¥¬ë ¢å®¤¨â å®âï ¡ë ®¤- ® ¥«¨¥©®¥ §¢¥®, â® ¨ ¢áï á¨á⥬ ¢ 楫®¬ áâ ®¢¨âáï ¥«¨¥©®©. â® ¤ ¥â ®á®¢ ¨¥ ¨®£¤ ®¯à¥¤¥«ïâì «¨¥©- ë¥ á¨á⥬ë, ª ª á¨á⥬ë, á®áâ®ï騥 ⮫쪮 ¨§ «¨¥©ëå §¢¥ì¥¢. ¥«¨¥©®© á¨á⥬®© ⮣¤ §ë¢ ¥âáï á¨á⥬ , á®- ¤¥à¦ é ï å®âï ¡ë ®¤¨ ¥«¨¥©ë© í«¥¬¥â.
1 ª®¥ ®¯à¥¤¥«¥¨¥ «¨¥©®© á¨á⥬ë ï¥âáï ¤®áâ â®ç® ®¡- 騬. ® ¯à¨¬¥¨¬® ª ª ª ª®¥ç®¬¥àë¬, â ª ¨ ª ¡¥áª®¥ç®¬¥àë¬ ¤¨ää¥à¥æ¨ «ìë¬ á¨á⥬ ¬, â ª¦¥ ª ¤¨áªà¥âë¬ á¨á⥬ ¬. ¤ ª® ®® ï¥âáï ¥ ᮢᥬ ¯®«ë¬, â ª ª ª ¥ ®âà ¦ ¥â ¢«¨ï¨ï ç «ì®£® á®áâ®ï¨ï. ®«®¥ ®¯à¥¤¥«¥¨¥ ᢮©á⢠«¨¥©®á⨠á¨á⥬ ¡ã¤¥â ¤ ® ¨¦¥, ¢ 10.3.1.
220

«¥¤г¥в ¯®¤з¥аªгвм, зв® ¢б¥ а¥ «мл¥ б¨бв¥¬л п¢«повбп ¥«¨¥©л¬¨. ¨§¨з¥бª¨¬ §¢¥мп¬ б¢®©бв¢¥л п¢«¥¨п блй¥¨п, £¨бв¥а¥§¨б , «одв ¨ в.¤. ¤ ª® «¨¥©л¬ б¨- бв¥¬ ¬ ¥ б«гз ©® г¤¥«¥® в ª®¥ ¡®«ми®¥ ¢¨¬ ¨¥ ¢ в¥- ®а¨¨ б¨бв¥¬. а¥¦¤¥ ¢б¥£®, в¥®а¨п «¨¥©ле б¨бв¥¬ ¤®- бв в®з® ¯а®бв . ®¦® ¤ ¦¥ бз¨в вм ¥¥ ¯а ªв¨з¥бª¨ § - ¢¥аи¥®©. ¥®а¨п ¥«¨¥©ле б¨бв¥¬ бгй¥бв¢¥® б«®¦- ¥¥, § з¨в¥«мл¥ гб¨«¨п ¯® ¨бб«¥¤®¢ ¨о ¥«¨¥©ле б¨- бв¥¬ ®¡лз® ¯а¨¢®¤пв ª ¬¥¥¥ ¤¥в «м®¬г ®¯¨б ¨о ¯а®- ж¥бб®¢, з¥¬ ¢ «¨¥©®¬ б«гз ¥. ¥«¨¥©л¥ б¨бв¥¬л ¬®£гв ®¡« ¤ вм в ª®© б«®¦®бвмо ¨ в ª¨¬ а §®®¡а §¨¥¬ б¢®©бв¢, зв® ¯а¥¤бв ¢«п¥вбп ¥¢®§¬®¦л¬ £®¢®а¨вм ® § ¢¥аи¥¨¨ в¥- ®а¨¨ в ª¨е б¨бв¥¬ ¢ ®¡®§а¨¬®¬ ¡г¤гй¥¬. ®¥з®, ¯а®бв®в ¨бб«¥¤®¢ ¨п ¥ п¢«п¥вбп б ¬ ¯® б¥¡¥ ¤®бв в®зл¬ ®б®¢- ¨¥¬ ¤«п ¯а¨¬¥¥¨п «¨¥©®© в¥®а¨¨. ¤ ª® ®з¥м ¢® ¬®£¨е б«гз пе ¨б¯®«м§®¢ ¨¥ «¨¥ а¨§®¢ ®© ¬®¤¥«¨ ¤ - ¥в ¯а ªв¨з¥бª¨ в¥ ¦¥ а¥§г«мв вл, зв® ¨ ¯а¨¬¥¥¨¥ ¡®«¥¥ в®з®© ¥«¨¥©®© ¬®¤¥«¨. «¥¤г¥в в ª¦¥ гз¥бвм, зв® ¯а¨ б®бв ¢«¥¨¨ ¬®¤¥«¨ б¨бв¥¬л ¥¨§¡¥¦® ¢®§¨ª ов ®и¨¡ª¨, б¢п§ л¥, ¯а¨¬¥а, б ¯®£а¥и®бвмо ®¯а¥¤¥«¥¨п § з¥¨©
¯ à ¬¥â஢ ®¡ê¥ªâ . «¨ï¨¥ íâ¨å ®è¨¡®ª ¬®¦¥â ®ª § âìáï ¡®«¥¥ áãé¥á⢥ë¬, 祬 ¯®£à¥è®á⥩, ¢ë§¢ ëå «¨¥ à¨- § 樥© ¬®¤¥«¨. ¯à¥¤¥«¥ë¬ ⥮à¥â¨ç¥áª¨¬ ®¡®á®¢ ¨¥¬ ¯à¨¬¥¨¬®á⨠«¨¥©®© ⥮ਨ á¨á⥬ á«ã¦¨â ¯¥à¢ë© ¬¥â®¤. . ï¯ã®¢ , ᮣ« á® ª®â®à®¬ã ¯à¨ "£« ¤ª®©" ¥«¨¥©- ®© å à ªâ¥à¨á⨪¥ ãá⮩稢®áâì ¥«¨¥©®© á¨áâ¥¬ë ¬®¦-
® ¨áá«¥¤®¢ âì ¯® ¯¥à¢®¬ã («¨¥©®¬ã) ¯à¨¡«¨¦¥¨î [34]. 2®íâ®¬ã ¯à ªâ¨ª¥ ®¡ëç® ¢ë¯®«ï¥âáï ¯à¥¤¢ à¨â¥«ì®¥ ¨áá«¥¤®¢ ¨¥ «¨¥ ਧ®¢ ®© ¬®¤¥«¨, ¤«ï ª®â®à®© ¨ ¯à®- ¨§¢®¤¨âáï á¨â¥§ § ª® ã¯à ¢«¥¨ï. ⥬ ®áãé¥á⢫ï¥âáï «¨§ ¯®«ã祮© á¨á⥬ë á ¨á¯®«ì§®¢ ¨¥¬ ¡®«¥¥ ¯®«®©, ¥«¨¥©®©, ¬®¤¥«¨. ® ¬®£¨å á«ãç ïå ®ª §ë¢ ¥âáï, çâ® ¥«¨¥©ë¥ ᢮©á⢠á¨áâ¥¬ë ¥ ¨£à îâ áãé¥á⢥®© à®- «¨. ਠ⠪®¬ ¯®¤å®¤¥ 楫¥á®®¡à §® ®¡¥á¯¥ç¨¢ âì ¢ë¯®«-
2 ¯®¬¨¬, çâ®, ᮣ« á® ¯¥à¢®¬ã ¬¥â®¤ã ï¯ã®¢ , ¥á«¨ «¨¥ ਧ®- ¢ ï á¨á⥬ ᨬ¯â®â¨ç¥áª¨ ãá⮩稢 , â® á®áâ®ï¨¥ à ¢®¢¥á¨ï ¥- «¨¥©®© á¨á⥬ë ãá⮩稢® ¢ ¬ «®¬= ¥á«¨ «¨¥ ਧ®¢ ï á¨á⥬ ¥ãá⮩稢 , â® ¥ãá⮩稢® ¨ á®áâ®ï¨¥ à ¢®¢¥á¨ï ¥«¨¥©®© á¨áâ¥- ¬ë= ¥á«¨ «¨¥ ਧ®¢ ï á¨á⥬ 室¨âáï " £à ¨æ¥ ãá⮩稢®áâ¨", â® ¥«ì§ï ¨áá«¥¤®¢ âì ãá⮩稢®áâì á®áâ®ï¨ï à ¢®¢¥á¨ï ¯® ¯¥à¢®¬ã ¯à¨¡«¨¦¥¨î.
221
