
Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления
.pdf
«î¡®¬ ¢å®¤®¬ ¢®§¤¥©á⢨¨ ¬®¦® ¯®«ãç¨âì ª ª á㬬㠯¥à¥- 室®© ¨ ¢ë㦤¥®© á®áâ ¢«ïîé¨å. ¥à¥å®¤ ï á®áâ ¢«ï-
îé ï S |
(x0 \ O) ¥áâì ¯à®æ¥áá, ¯®«ãç¥ë© ¯à¨ ã«¥¢®¬ ¢å®¤¥ |
|||
¨ § ¤ ëå ç «ìëå ãá«®¢¨ïå x0, ¢ë㦤¥ ï á®áâ ¢«ï- |
||||
îé ï S |
; |
0\ u[t0 t] |
|
¥áâì ॠªæ¨ï á¨áâ¥¬ë § ¤ ®¥ ¢å®¤®¥ |
¢®§¤¥©á⢨¥ ¯à¨ ã«¥¢ëå ç «ìëå ãá«®¢¨ïå.
¢®©á⢮ (10.11) ¯à¨¢®¤¨â ª ⮬ã, çâ® å à ªâ¥à ᮡá⢥- ëå ¤¢¨¦¥¨© á¨áâ¥¬ë ¥ § ¢¨á¨â ®â à §¬¥à®¢ ®¡« á⨠¯à®- áâà á⢠á®áâ®ï¨©, ¢ ª®â®à®© í⨠¤¢¨¦¥¨ï à áᬠâਢ -
îâáï. ®«¥¥ â®ç®, ¯®« £ ï ¢ (10.11) x00 = x0 x000 = 0 ¯®«ã稬 ¤«ï ¢á¥å k x0
S(kx0\ O) = kS(x0 \ O):
«¥¤®¢ ⥫ì®, ¢¨¤ ä §®¢ëå ¯®àâà¥â®¢ «¨¥©ëå áâ 樮 à- ëå á¨á⥬ ¥ § ¢¨á¨â ®â à §¬¥à ®ªà¥áâ®áâ¨ ç « ª®®à- ¤¨ â { íâ¨ ä §®¢ë¥ ¯®àâà¥âë ¬®¦® ¯à¥®¡à §®¢ âì ¤à㣠ª ¤àã£ã ¨§¬¥¥¨¥¬ ¬ áèâ ¡ .
®¢®ªã¯®á⨠íâ¨å ᢮©á⢠(«¨¡® ®¤®£® ¨§ ¨å) «¨è¥ë ¥«¨¥©ë¥ á¨á⥬ë. â® ¯à¨¢®¤¨â ª íä䥪⠬, ¥ª®â®àë¥ ¨§ ª®â®àëå à áᬮâà¥ë ¨¦¥. ᮢ®¥ ¢¨¬ ¨¥ 㤥«¨¬ ᮡáâ¢¥ë¬ ¤¢¨¦¥¨ï¬ ¢ ¥«¨¥©ëå á¨á⥬ å { å à ªâ¥à ¢ë㦤¥ëå ¯à®æ¥áᮢ ®ª §ë¢ ¥âáï ¥é¥ ¡®«¥¥ á«®¦ë¬ ¨ à §®®¡à §ë¬.
10.3.2. ¥¯ à âà¨áë¥ ¯®¢¥àå®áâ¨
ª ®â¬¥ç¥® ¢ëè¥, ã ¥«¨¥©ëå á¨á⥬ ¬®¦¥â ¡ëâì à §- «¨çë© å à ªâ¥à ᮡá⢥ëå ¤¢¨¦¥¨© ¢ à §ëå ®¡« áâïå ¯à®áâà á⢠á®áâ®ï¨©. ®í⮬㠯ਠ¨áá«¥¤®¢ ¨¨ â ª¨å á¨á⥬ ¥¤®áâ â®ç®, ¢®®¡é¥ £®¢®àï, à áᬠâਢ âì «¨èì ¥ª®â®àãî ®ªà¥áâ®áâì á®áâ®ï¨ï à ¢®¢¥á¨ï { ¨áá«¥¤®¢- ¨¥ ¤®«¦® ®å¢ âë¢ âì ¢á¥ ¢®§¬®¦ë¥ ®¡« á⨠¯à®áâà - á⢠á®áâ®ï¨©. áâ¥á⢥®, íâ® á¨«ì® ãá«®¦ï¥â «¨§.ਠ¨á¯®«ì§®¢ ¨¨ ç¨á«¥ëå ¬¥â®¤®¢ ¨áá«¥¤®¢ ¨ï ( ¯à¨- ¬¥à, ¬®¤¥«¨à®¢ ¨ï ) ª®«¨ç¥á⢮ ¢ëç¨á«¥¨© ®ª - §ë¢ ¥âáï § ç¨â¥«ì® ¢ëè¥, 祬 ¤«ï «¨¥©ëå á¨á⥬. â® ¯®ª §ë¢ ¥â ¥®¡å®¤¨¬®áâì à §¢¨â¨ï «¨â¨ç¥áª¨å ¬¥â®¤®¢ ¨áá«¥¤®¢ ¨ï.
ª ç¥á⢥ ¨««îáâà 樨 à áᬮâਬ á«¥¤ãî騩 ¯à®á⮩ ¯à¨¬¥à. ãáâì á¨á⥬ ®¯¨áë¢ ¥âáï ãà ¢¥¨¥¬
x(t) = x(t)2 ; x(t) x(0) = x0:
232

¨á⥬ ¨¬¥¥â ¤¢ |
á®áâ®ï¨ï à ¢®¢¥á¨ï: x |
= 0 ¨ x = 1: ¥- |
||
|
|
|
1 |
2 |
âà㤮 ã¡¥¤¨âìáï, çâ® ¯à¨ x0 < 1 § ª¨ x(t) ¨ x(t) ¯à®â¨¢®¯®- |
||||
«®¦ë ¨ à¥è¥¨¥ ¡ã¤¥â áâ६¨âìáï ª â®çª¥ x1 x(t) ! 0: ਠ|
||||
x0 > 1 ¢ë¯®«¥® x(t) > 0 ¨ à¥è¥¨¥ à á室¨âáï, x(t) ! 1 |
||||
(¯à¨ç¥¬ § 票¥ x(t) áâ ®¢¨âáï ¥®£à ¨ç¥® ¡®«ì訬 § |
||||
ª®¥ç®¥ ¢à¥¬ï). |
ª¨¬ ®¡à §®¬, |
x1 { ãá⮩稢®¥ á®áâ®ï- |
||
¨¥ à ¢®¢¥á¨ï, |
x2 { ¥ãá⮩稢®¥. ®çª |
x = 1 à §¤¥«ï¥â |
||
¯à®áâà á⢮ á®áâ®ï¨© X |
= R |
®¡« á⨠á ãáâ®©ç¨¢ë¬ ¨ |
||
¥ãáâ®©ç¨¢ë¬ å à ªâ¥à®¬ ¯®¢¥¤¥¨ï. |
|
|||
¯à¥¤¥«¥¨¥ [79]. ®¢¥àå®áâì, à §¤¥«ïîé ï ¯à®áâà - |
||||
á⢮ á®áâ®ï¨© á¨á⥬ë |
®¡« á⨠á à §ë¬¨ ⨯ ¬¨ ä - |
|||
§®¢ëå âà ¥ªâ®à¨© (â.¥. ¢¨¤®¢ ᮡá⢥ëå ¤¢¨¦¥¨©) §ë- ¢ ¥âáï ᥯ à âà¨á®© ¯®¢¥àå®áâìî (¯à¨ n = 2 à §¤¥«ïîé ï ¯®¢¥àå®áâì ï¥âáï ¥ª®â®à®© ªà¨¢®©, §ë¢ ¥¬®© ᥯ à -
âà¨á®©). 2
®«¥¥ â®ç®¥ ®¯à¥¤¥«¥¨¥ { ᥯ à âà¨á ï ¯®¢¥àå®áâì ¥áâì ¯®¢¥àå®áâì, ïîé ïáï «¨¡® í«¥¬¥â®¬ ¯à¨â殮¨ï, «¨¡® í«¥¬¥â®¬ ®ââ «ª¨¢ ¨ï ¤«ï ¢á¥å ¡«¨§ª¨å âà ¥ªâ®à¨©.
®£¤ (ª ª ¢ ¯à¨¢¥¤¥®¬ ¯à¨¬¥à¥) ᥯ à âà¨á®© ï¥â- áï ¥ª®â®à ï ä §®¢ ï âà ¥ªâ®à¨ï. ®§¬®¦® â ª¦¥, çâ® á¥-
¯ а ва¨бл ®¡а §говбп ¨§ гз бвª®¢ а §«¨зле ва ¥ªв®а¨© (а¨б. 10.2, ). 11.6. а бᬮва¥л б¨бв¥¬л, ¤«п ª®в®але ¤¢¨¦¥¨¥ ¯а®¨б室¨в ¯® б¥¯ а ва¨б®© ¯®¢¥ае®бв¨, ® б - ¬® ¯®пв¨¥ б®®в¢¥вбв¢гой¥£® а¥и¥¨п га ¢¥¨© 㦤 ¥вбп ¢ ¤®¯®«¨в¥«м®¬ ®¯а¥¤¥«¥¨¨.
10.3.3. ।¥«ìë¥ æ¨ª«ë. ¢â®ª®«¥¡ ¨ï
«ï ¥ª®â®àëå á¨á⥬ ¬®£ãâ, ª ª ¨§¢¥áâ®, áãé¥á⢮¢ âì ¯¥- ਮ¤¨ç¥áª¨¥ ¯à®æ¥ááë á ¯¥à¨®¤®¬ T â ª¨¥, çâ® x(t) = x(t +T) (¡®«¥¥ ¯®¤à®¡®¥ ®¯à¥¤¥«¥¨¥ ¯¥à¨®¤¨ç¥áª¨å ¯à®æ¥áᮢ ¤ - ® ¢ëè¥ ¢ 5.1. ¨ [79, 93]). ®®â¢¥âáâ¢ãî騥 ¨¬ ä §®¢ë¥ âà ¥ªâ®à¨¨ ¯à¥¤áâ ¢«ïîâ ᮡ®© § ¬ªãâë¥ ªà¨¢ë¥. «ï áâ 樮 àëå «¨¥©ëå á¨á⥬ ¯¥à¨®¤¨ç¥áª¨¥ ᮡáâ¢¥ë¥ ¤¢¨¦¥¨ï ¨¬¥îâ ¬¥áâ®, ¥á«¨ å à ªâ¥à¨áâ¨ç¥áª¨© ¬®£®ç«¥ A(s) = 0 ¯à¨ ¥ª®â®à®¬ s = | . ( ¥à¨®¤ T = 2 = :) ª®© ¢¨¤ ¤¢¨¦¥¨© ᢮©á⢥, ¯à¨¬¥à, ª®«¥¡ ⥫ìë¬ ª®á¥à¢ ⨢- ë¬ §¢¥ìï¬.
¦® ®в¬¥в¨вм, зв® ª®«¥¡ ¨п, ¢®§¨ª ой¨¥ г «¨¥©ле б¨бв¥¬, п¢«повбп ¥£àã¡ë¬¨ ¢ ⮬ á¬ëá«¥, ç⮠᪮«ì 㣮¤® ¬ «®¥ ®âª«®¥¨¥ ¯ à ¬¥â஢ á¨áâ¥¬ë ®â ¨á室ëå ¬®¦¥â
233
¨á. 10.2. ¥¯ à âà¨áë ¨ ¯à¥¤¥«ìë© æ¨ª«.
¯à¨¢¥á⨠ª ¨á祧®¢¥¨î ¯¥à¨®¤¨ç¥áª¨å ¤¢¨¦¥¨©. ஬¥ ⮣®, ¬ «®¥ ¨§¬¥¥¨¥ ç «ì®£® á®áâ®ï¨ï á¨áâ¥¬ë ¯à¨¢®- ¤¨â ª ¯à®¯®à樮 «ì®¬ã ¨§¬¥¥¨î ¬¯«¨âã¤ë ª®«¥¡ ¨©, ª ª íâ® ¢¨¤® ¨§ ä®à¬ã«ë ®è¨ (6.8) ¤«ï à¥è¥¨© «¨¥©- ëå á¨á⥬. ¥«¨¥©ëå á¨á⥬ ¢®§¬®¦® áãé¥á⢮¢ ¨¥ £àã¡ëå ¯¥à¨®¤¨ç¥áª¨å ¯à®æ¥áᮢ, å à ªâ¥à¨á⨪¨ ª®â®àëå ¥
¬¥повбп (ª з¥бв¢¥®) ¯а¨ ¨§¬¥¥¨¨ ¢ ®¯а¥¤¥«¥ле ¯а¥- ¤¥« е ¯ а ¬¥ва®¢ ¨«¨ з «мле гб«®¢¨©. бᬮва¨¬ нв® п¢«¥¨¥ ¯®¤а®¡¥¥.
ãáâì ¢â®®¬ ï á¨á⥬ ®¯¨áë¢ ¥âáï ãà ¢¥¨¥¬
x(t) = f;x(t) : |
(10.12) |
¯à¥¤¥«¥¨¥ [79]. ¥à¨®¤¨ç¥áª®¥ à¥è¥¨¥ x(t) |
â ª¦¥ á®- |
®â¢¥âáâ¢ãîé ï ¥¬ã âà ¥ªâ®à¨ï G áç¨â ¥âáï ¨§®«¨à®¢ ë¬ ¯¥à¨®¤¨ç¥áª¨¬ à¥è¥¨¥¬ ¨ §ë¢ ¥âáï ¯à¥¤¥«ìë¬ æ¨ª«®¬, ¥á«¨ áãé¥áâ¢ã¥â â ª®¥ > 0, çâ® ª ª®¢ ¡ë ¨ ¡ë« â®çª
x0 |
2 X |
室ïé ïáï ®â ªà¨¢®© |
G |
|
¯®«®¦¨â¥«ì®¬ à ááâ®ï- |
|||||
|
0 |
), |
7 |
¬¥ì襬, 祬 0 |
|
0 |
) < \ ¯à®å®¤ï饥 ç¥à¥§ |
|||
¨¨ G(x |
|
< G(x |
||||||||
¥¥ à¥è¥¨¥ ãà ¢¥¨ï (10.12) |
¥ ï¥âáï ¯¥à¨®¤¨ç¥áª¨¬. |
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
7 ááâ®ï¨¥ G(x) ®â â®çª¨ x ¤® ªà¨¢®© G ¢ ¯à®áâà á⢥ Rn ¬®¦® |
|||||||||
|
(jjx |
; xGjj), £¤¥ jj jj { ¥ª®â®à ï ( ¯à¨¬¥à, |
®¯à¥¤¥«¨âì ª ª G(x) = infxG 2G |
||
¥¢ª«¨¤®¢ ) ¢¥ªâ®à ï ®à¬ ¢ Rn: |
|
|
|
|
234 |

â® ®§ ç ¥â, çâ® ¯à¨ n = 2 ä §®¢®© ¯«®áª®á⨠¢¡«¨§¨ ¯à¥¤¥«ìëå 横«®¢ ¥ ¯à®å®¤¨â ¤àã£¨å § ¬ªãâëå âà ¥ªâ®- ਩ à¥è¥¨© ãà ¢¥¨ï (10.12). ⬥⨬, çâ® ã «¨¥©ëå ª®á¥à¢ ⨢ëå á¨á⥬ § ¬ªãâë¥ âà ¥ªâ®à¨¨ «¥¦ â "¢áî- ¤ã ¯«®â®" { ᪮«ì 㣮¤® ¬ «®¬ à ááâ®ï¨¨ ®â ¤ ®© § ¬ªã⮩ ªà¨¢®© 室ïâáï ¤à㣨¥ § ¬ªãâë¥ âà ¥ªâ®à¨¨.
ª ¤«ï ¢¥è¨å, â ª ¨ ¤«ï ¢ãâà¥¨å ¯® ®â®è¥¨î ª
¯à¥¤¥«ì®¬ã 横«ã G 8 ¨¬¥îâáï |
¤¢¥ ¢§ ¨¬® ¨áª«îç î騥 |
¢®§¬®¦®á⨠¯®¢¥¤¥¨ï ¢¡«¨§¨ G |
: ¢á¥ ¢ãâ२¥ âà ¥ªâ®- |
ਨ, ç¨ î騥áï ¢¡«¨§¨ G " ¬ âë¢ îâáï" G ª ª ᯨ- |
|
à «¨ «¨¡® ¯à¨ t ! 1 «¨¡® ¯à¨ t |
! ;1: ® ¦¥ á ¬®¥ ®â®- |
á¨âáï ¨ ª® ¢¥è¨¬ âà ¥ªâ®à¨ï¬ |
[79]. |
᫨ ¢á¥ ¢ãâ२¥ ¨ ¢¥è¨¥ âà ¥ªâ®à¨¨, ç¨ îé¨- ¥áï ¢¡«¨§¨ G " ¬ âë¢ îâáï" G ¯à¨ t ! 1 â® ¯à¥¤¥«ì- ë© æ¨ª« §ë¢ ¥âáï ãá⮩稢ë¬. ®®â¢¥âá⢥®, ¢®§¬®¦-
ë (¢¯®«¥) ¥ãáâ®©ç¨¢ë¥ ¨ ¯®«ããáâ®©ç¨¢ë¥ ¯à¥¤¥«ìë¥ æ¨-
ª«ë. |
|
¯à¥¤¥«¥¨¥ ( . . ¤à®®¢, á¬. [79]). áâ®©ç¨¢ë© |
|
¯à¥¤¥«ìë© æ¨ª« §ë¢ ¥âáï ¢â®ª®«¥¡ ¨¥¬. |
2 |
ª¨¬ ®¡à §®¬, ¢â®ª®«¥¡ ¨ï ¯à¥¤áâ ¢«ïîâ ᮡ®© ¯à®-
æ¥áá, å à ªâ¥àë© ¨áª«îç¨â¥«ì® ¤«ï ¥«¨¥©ëå á¨á⥬.à ªâ¨ç¥áª¨ ¬®¦® áç¨â âì, çâ® â ª®© ¯à®æ¥áá ¨¬¥¥â ¬¥áâ®, ª®£¤ á®áâ®ï¨¥ à ¢®¢¥á¨ï á¨áâ¥¬ë ¥ãá⮩稢® "¢ ¬ «®¬",
® á¨á⥬ ®¡« ¤ ¥â ¤¨áᨯ ⨢®áâìî, |
â ª çâ® ¯à®æ¥ááë |
||
¯à¨ "¡®«ìè¨å" ç «ìëå ®âª«®¥¨ïå § âãå îâ. |
ª ç¥- |
||
á⢥ ¯à¨¬¥à |
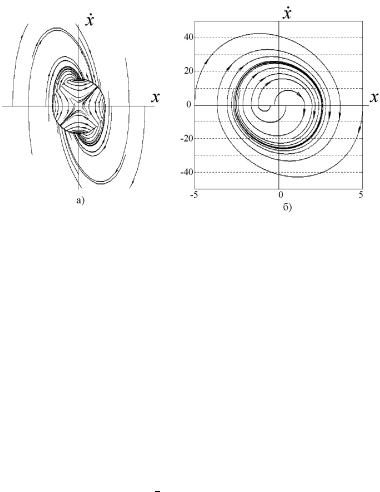
à¨á. 10.2, ¡ ¯®ª § ä §®¢ë© ¯®àâà¥â ¢- |
||
⮪®«¥¡ ⥫쮩 á¨á⥬ë T 2x + 2 Tx + x = ku u |
= c signx |
||
(T = 0:1 c, |
= 0:25), ïî饩áï ã¯à®é¥®© ¬®¤¥«ìî £¥- |
||
¥à â®à ª®«¥¡ ¨© [79, 94]. â á¨á⥬ |
¨áá«¥¤ã¥âáï ¨¦¥ |
||
¢ ¯.¯. 11.2.2. 11.3. ¬¥â¨¬, çâ® ¯à¥¤¥«ìë© æ¨ª« ï¥âáï ¨ ᥯ à âà¨á®©.
¥«¨¥©ë¬ á¨á⥬ ¬ ᢮©áâ¢¥ë ¥ ⮫쪮 ¯¥à¨®¤¨ç¥- ᪨¥ ᮡáâ¢¥ë¥ ¯à®æ¥ááë. ®§¬®¦ë â ª¦¥ ª¢ §¨¯¥à¨®¤¨- ç¥áª¨¥ ०¨¬ë, ᮮ⢥âáâ¢ãî騥 ª®«¥¡ ⥫ìë¬ ¤¢¨¦¥¨- ï¬ á ¥á®¨§¬¥à¨¬ë¬¨ ç áâ®â ¬¨. ®«¥¥ ⮣®, ¢®§¬®¦® ¢®§- ¨ª®¢¥¨¥ å ®â¨ç¥áª¨å ª®«¥¡ ⥫ìëå ¯à®æ¥áᮢ, ¨¬¥îé¨å ¥¯à¥àë¢ë© ᯥªâà ç áâ®â ¨, á«¥¤®¢ ⥫ì®, ®¡« ¤ îé¨å ᢮©á⢠¬¨, å à ªâ¥à묨 ¤«ï á«ãç ©ëå ¯à®æ¥áᮢ. áâ -
8 «ï ¯à®áâ®âë ¨§«®¦¥¨ï ᥩç á à áᬠâਢ ¥¬ á«ãç © ä §®¢®© ¯«®áª®áâ¨, n = 2:
235

®¢¨¢è¨¥áï å ®â¨ç¥áª¨¥ ¯à®æ¥ááë ®â«¨ç îâáï ®â ¯à¥¤¥«ì- ëå 横«®¢ ¨ ®¯¨áë¢ îâáï ¯à¨â¢ î騬¨ ¬®¦¥á⢠¬¨ { ââà ªâ®à ¬¨. ¢¥¤¥¨ï ® å ®â¨ç¥áª¨å á¨á⥬ å ¨ ¬¥â®¤ å ¨å ¨áá«¥¤®¢ ¨ï ¯à¨¢¥¤¥ë ¢ ¯. 13.3.
¨¡®«¥¥ ®¡é¥¥ ¨§ ¨§¢¥áâëå ®¯à¥¤¥«¥¨© ª®«¥¡ ⥫ìëå ¯à®æ¥áᮢ, ¢ª«îç î饥 ª ª ¯¥à¨®¤¨ç¥áª¨¥, â ª ¨ ¥à¥£ã«ïà- ë¥, å ®â¨ç¥áª¨¥, ¯à¥¤«®¦¥® . . ªã¡®¢¨ç¥¬ ¢ 1973 £. (á¬.
[55, 56, 76, 93])
¯à¥¤¥«¥¨¥ . ¥è¥¨¥ x(t) (t) á¨á⥬ë (10.8), (10.9) §ë¢ ¥âáï ª®«¥¡ ⥫ìë¬ (¨«¨ ª®«¥¡ ⥫ìë¬ ¯® ªã¡®¢¨-
çã) ¯® ¢ë室ã , |
¥á«¨ ¢ë¯®«¥ë á«¥¤ãî騥 ãá«®¢¨ï: 1) |
||
jjx(t)jj |
const\ 2) ¨á«® ¨§¬¥¥¨© § ª |
äãªæ¨¨ (t) ¡¥á- |
|
ª®¥ç® t 2 [0 |
1)\ 3) ¨á«® ¢ë室®¢ (t) § ¯à¥¤¥«ë § - |
||
¤ ®£® ¨â¥à¢ « |
[; ] > 0 > |
0, ¡¥áª®¥ç® |
|
t 2 [0 1): |
2 |
|
|
10.3.4. ®áâ®ï¨ï à ¢®¢¥á¨ï. â१ª¨ ¯®ª®ï
¡à ⨬áï ⥯¥àì ª á®áâ®ï¨ï¬ à ¢®¢¥á¨ï ¥«¨¥©ëå á¨- á⥬. ëè¥ ¡ë«® ®â¬¥ç¥®, çâ® â ª¨¬¨ á®áâ®ï¨ï¬¨ ï-
îâáï ®á®¡ë¥ â®çª¨, |
¢ ª®â®àëå ¢¥ªâ®à |
ä §®¢®© ᪮à®á⨠|
v ®¡à é ¥âáï ¢ ®«ì. |
«ï «¨¥©ëå áâ |
樮 àëå á¨á⥬ |
x(t) = Ax(t) ¢ë¯®«¥® v(x) = Ax ¯®í⮬㠬®¦¥á⢮ á®áâ®ï- ¨© à ¢®¢¥á¨ï fx g { «¨¡® ç «® ª®®à¤¨ â (¯à¨ det A 6= 0),
«¨¡® ¬®£®®¡à §¨¥ ¡®«¥¥ ¢ë᮪®© à §¬¥à®áâ¨, ® ¢á¥£¤ { ¥ª®â®à®¥ «¨¥©®¥ ¯®¤¯à®áâà á⢮ ( 㫨à㥬®¥ ¯®¤¯à®-
áâà á⢮ |
N |
(A) ¬ âà¨æë A) ¯à®áâà á⢠|
á®áâ®ï¨©, |
|
|
|
|
á. 113. |
|
fx |
g = N (A) N (A) X á¬. á®áªã 3 |
|||
«п ¥«¨¥©ле б¨бв¥¬ ®б®¡л¥ в®зª¨ ®¯а¥¤¥«повбп ¨§ |
||||
ãà ¢¥¨ï (10.12), ᮣ« á® ª®â®à®¬ã á®áâ®ï¨ï à ¢®¢¥á¨ï x ¤®«¦ë 㤮¢«¥â¢®àïâì ¥«¨¥©®¬ã «£¥¡à ¨ç¥áª®¬ã ãà ¢- ¥¨î (â®ç¥¥ { á¨á⥬¥ ãà ¢¥¨© ®â®á¨â¥«ì® ª®¬¯®¥â xi ¢¥ªâ®à x ):
f(x ) = 0: |
(10.13) |
âáî¤ ¢¨¤®, çâ® ¢ § ¢¨á¨¬®á⨠®â ¯à ¢ëå ç á⥩ ãà ¢- ¥¨ï (10.12), ¬®¦¥á⢮ á®áâ®ï¨© à ¢®¢¥á¨ï fx g ¬®£ãâ ¨¬¥âì á«®¦ãî áâàãªâãàã. â® ¬®¦¥â ¡ëâì ᮢ®ªã¯®áâì ¨§®«¨à®¢ ëå â®ç¥ª «¨¡® ®â१®ª ¯àאַ© ("®â१®ª ¯®ª®ï"),
ç áâì ¯«®áª®á⨠("¯« á⨪ ¯®ª®ï", "§® § áâ®ï") ¨ â.¤.
236

«ï ¨««îáâà 樨 à¨á. 10.3 ¯à¨¢¥¤¥ë ¯à¨¬¥àë ä §®- ¢ëå ¯®àâà¥â®¢ á¨á⥬ á ¬®¦¥á⢮¬ ¨§®«¨à®¢ ëå á®áâ®ï- ¨© à ¢®¢¥á¨ï ( ) ¨ á ®â१ª®¬ ¯®ª®ï (¡). 9
¨á. 10.3. ®áâ®ï¨ï à ¢®¢¥á¨ï ¥«¨¥©ëå á¨á⥬.
10.3.5.¥¥¤¨á⢥®áâì à¥è¥¨©. ¥à¥á¥ç¥¨¥ âà ¥ªâ®- ਩
ª ¨§¢¥áâ® ¨§ ⥮ਨ ¤¨ää¥à¥æ¨ «ìëå ãà ¢¥¨© [12], ãà ¢¥¨¥ (10.12) ¨¬¥¥â à¥è¥¨¥, ¯à¨â®¬ ¥¤¨á⢥®¥, ¯à¨ ¢ë¯®«¥¨¨ â ª §ë¢ ¥¬®£® ãá«®¢¨ï ¨¯è¨æ , ᮣ« á® ª®- â®à®¬ã ¤«ï ¢á¥å x0 x00 2 X áãé¥áâ¢ã¥â ª®áâ â (ª®áâ ⨯è¨æ ) L > 0 (L < 1) ¥ § ¢¨áïé ï ®â x0 x00 çâ® ¨¬¥¥â
¬¥áâ®
jjf(x0) ; f(x00)jj Ljjx0 ; x00jj: |
(10.14) |
â® ã⢥ত¥¨¥ ï¥âáï ®¤®© ¨§ ⥮६ ® áãé¥á⢮¢ ¨¨ ¨ ¥¤¨á⢥®á⨠à¥è¥¨© ®à¬ «ì®© á¨áâ¥¬ë ¤¨ää¥à¥æ¨- «ìëå ãà ¢¥¨© (10.12) [12, 79]. á«®¢¨¥ ¨¯è¨æ ®§ ç - ¥â, çâ® äãªæ¨ï f(x) ¥ ¤®«¦ ¨§¬¥пвмбп ¢ «о¡®© ®¡« бв¨ ¯а®бва бв¢ X ¡ëáâ॥ ¥ª®â®à®© «¨¥©®© äãªæ¨¨ á ª®- áâ ⮩, ¥ § ¢¨áï饩 ®â ¢ë¡®à ®¡« áâ¨.
«ï «¨¥©ëå á¨á⥬ ãá«®¢¨¥ (10.14), ®ç¥¢¨¤®, ¢ë¯®«¥- ®, çâ® ¯®§¢®«¨«® ¢ ¯. 5.1. áä®à¬ã«¨à®¢ âì ®¡é¨¥ ᢮©áâ¢
9 |
{ ä §®¢ë© ¯®àâà¥â á¨á⥬ë x + 0:5x + 5 sin x = 0= ¡ { á¨á⥬ë |
|
|
x + signx + x = 0: |
|
|
237 |

д §®¢ле ¯®ава¥в®¢ в ª¨е б¨бв¥¬. «п ¥«¨¥©ле б¨бв¥¬ гб«®¢¨¥ ¨¯и¨ж ¬®¦¥в ¡лвм аги¥®. ¯а¨¬¥а, б¨бв¥- ¬ ¬®¦¥в ᮤ¥а¦ вм "а §ал¢го" (а¥«¥©го) ¥«¨¥©®бвм.®£¤ ¢ ®ªа¥бв®бв¨ в®з¥ª а §ал¢ ¯а ¢л¥ з бв¨ га ¢¥- ¨п (10.12) а бвгв ¥®£а ¨з¥® ¡лбва®. аг£¨¬ ¯а¨¬¥а®¬ п¢«повбп ª¢ ¤а в¨зл¥, ªг¡¨зл¥ ¥«¨¥©®бв¨, ¯а®¨§¢¥¤¥- ¨п ¯¥а¥¬¥ле б®бв®п¨п ¢ f (x) ¨ â.¤. 10
§ ¢¨á¨¬®á⨠®â ¢¨¤ äãªæ¨¨ f(x) ¤«ï ¥«¨¥©ëå á¨- á⥬ ¢®§¬®¦ë à §ë¥ ¯à®æ¥ááë, ¢ë§¢ ë¥ àã襨¥¬ 㪠-
§ ®£® ãá«®¢¨ï. ¯à¨¬¥à, ¢®§¬®¦® ᫨逸 à §«¨çëå ä §®¢ëå âà ¥ªâ®à¨© ¢ ®¤ã. ª®© ¢¨¤ ¯®¢¥¤¥¨ï ᢮©á⢥, ¯à¥¦¤¥ ¢á¥£® á¨á⥬ ¬ á à §àë¢ë¬¨ ¥«¨¥©®áâﬨ. - ¯à¨¬¥à, ¢ ®¯â¨¬ «ìëå ¯® ¡ëáâத¥©á⢨î á¨á⥬ å ¢® ¬®- £¨å á«ãç ïå ¢á¥ âà ¥ªâ®à¨¨ ᫨¢ îâáï ¢ ®¤ã, ¯à®å®¤ïéãî ç¥à¥§ § ¤ ãî â®çªã [76]. á¨á⥬ å á ५¥©®-«®£¨ç¥áª¨¬ ã¯à ¢«¥¨¥¬ â ª¦¥ ¢®§¬®¦¥ ¯à¥¤¥«ìë© æ¨ª«, á®áâ®ï騩 ¨§ ãç á⪮¢ ä §®¢ëå ªà¨¢ëå, ª®â®àë© ¨§®¡à ¦ îé ï â®çª ¯®¯ ¤ ¥â ¨§ à §«¨çëå ç «ìëå ãá«®¢¨© § ª®¥ç®¥ ¢à¥- ¬ï (á¬. à¨á. 10.4, a). à ªâ¥à® â ª¦¥ ¯®ï¢«¥¨¥ ᪮«ì- §ïé¨å ०¨¬®¢, ¯à¨ ª®â®àëå à §ë¥ âà ¥ªâ®à¨¨ ¯®¯ ¤ îâ
з¥а¥§ ª®¥з®¥ ¢а¥¬п ¥ª®в®аго ¯®¢¥ае®бвм (¥ п¢«пойгобп, ¢®®¡й¥ £®¢®ап, а¥и¥¨¥¬ (10.12)). ª з бвл© б«г-
ç© ¤¢¨¦¥¨¥ ¯® ¥ª®â®à®© âà ¥ªâ®à¨¨ ¬®¦¥â § ª®¥ç®¥ ¢à¥¬ï ¯à¨¢¥á⨠ª á®áâ®ï¨î à ¢®¢¥á¨ï á¨á⥬ë. â® ®§ -
ç¥â, çâ® ¯¥à¥å®¤ë© ¯à®æ¥áá ¢ ¥¯à¥à뢮© ¥«¨¥©®© á¨- á⥬¥ ¬®¦¥â ¨¬¥âì ª®¥çãî ¤«¨â¥«ì®áâì, çâ® ¨áª«î祮
¤«ï áâ 樮 àëå ¥¯à¥àë¢ëå «¨¥©ëå á¨á⥬.
¬¥â¨¬, çâ® ¤«ï â ª¨å á¨á⥬ â¥àï¥âáï ¢®§¬®¦®áâì ®¯à¥- ¤¥«¨âì à §¢¨â¨¥ ¯à®æ¥áá ¢ ¯à®è«®¬ ¯® ¥£® ⥪ã饬ã á®áâ®- ï¨î. ¥¥ ¤¨ ¬¨ç¥áª¨¥ ¤¥â¥à¬¨¨à®¢ ë¥ á¨áâ¥¬ë ¡ë- «¨ ®¯à¥¤¥«¥ë ª ª á¨á⥬ë, ã ª®â®àëå ¯® ç «ì®¬ã á®- áâ®ï¨î ¨ ¢å®¤®¬ã ¯à®æ¥ááã ¬®¦® ®¤®§ ç® ®¯à¥¤¥«¨âì ¡ã¤ã饥 ¯®¢¥¤¥¨¥. ⬥祮¥ ¢ëè¥ á¢®©á⢮ ¥ ¯à®â¨¢®- à¥ç¨â ¤ ®¬ã ®¯à¥¤¥«¥¨î, â ª ª ª ¯®á«¥¤¥¥ ®â®á¨âáï ª ¡ã¤ã饬ã, ¥ ª ¯à®è«®¬ã à §¢¨â¨î ¯à®æ¥áá . áᬮâਬ
10 ®£¤ ¨á¯®«ì§ã¥âáï â ª §ë¢ ¥¬®¥ «®ª «ì®¥ ãá«®¢¨¥ ¨¯è¨æ (¢ ®â«¨ç¨¥ ®â £«®¡ «ì®£® (10.14)), ᮣ« á® ª®â®à®¬ã ª®áâ â L ¤®«¦- "®¡á«ã¦¨¢ âì" «¨èì ¥ª®â®àãî ®£à ¨ç¥ãî ®¡« áâì ¯à®áâà á⢠á®áâ®ï¨© [36]. ®£¤ , ¯à¨¬¥à ¤«ï f(x) = x2 ¢ë¯®«¥® «®ª «ì®¥ ãá«®- ¢¨¥ ¨¯è¨æ , ¤«ï f(x) = sign(x) ¢ ®ªà¥áâ®á⨠â®çª¨ 0 ®® ¥ ¢ë¯®«¥®.«®¡ «ì®¥ ãá«®¢¨¥ ¨¯è¨æ (10.14) ¥ ¢ë¯®«¥® ¢ ®¡®¨å á«ãç ïå.
238

⥯¥àì á«¥¤ãî騩 ¯à¨¬¥à.
ãáâì á¨á⥬ ®¯¨áë¢ ¥âáï ãà ¢¥¨¥¬ ¯¥à¢®£® ¯®à浪
|
|
x(t) = sign(x(t))p |
|
|
|
|
|
|
jx(t)j |
x(0) = x0: |
|
||
®«®¦¨¬ x0 = 0: 祢¨¤®, ãà ¢¥¨¥ ¨¬¥¥â âਢ¨ «ì®¥ à¥- |
||||||
襨¥ x1(t) |
|
0: ஬¥ ⮣®, ¥¯®á।á⢥®© ¯®¤áâ ®¢ª®© |
||||
|
|
t2 |
t2 |
â ª¦¥ ¥áâì |
||
ã¡¥¦¤ ¥¬áï, çâ® äãªæ¨¨ x2(t) = 4 ¨ x3(t) = ; 4 |
||||||
à¥è¥¨ï ¤ ®£® ãà ¢¥¨ï ¯à¨ 㪠§ ®¬ ç «ì®¬ ãá«®- |
||||||
¢¨¨. |
|
|
|
|
|
|
¬¥â¨¬, çâ® ¢ ¤ ®¬ ¯à¨¬¥à¥ ãá«®¢¨¥ ¨¯è¨æ |
àãè¥- |
|||||
® ¢ ®ªà¥áâ®áâ¨ ç « ª®®à¤¨ â. |
|
|
|
|||
«¥¤®¢ ⥫ì®, ¥«¨¥©®áâì ãà ¢¥¨© á¨áâ¥¬ë ¬®¦¥â ¯à¨¢¥á⨠ª á«®¦®á⨠¢ ®¯à¥¤¥«¥¨¨ á ¬®£® ¯®ïâ¨ï ¥¥ á®- áâ®ï¨ï. ®¥ç®, ¯à¨ â¥å¨ç¥áª®© ॠ«¨§ 樨 â ª®© á¨áâ¥- ¬ë ¨«¨ ¥¥ ¬®¤¥«¨à®¢ ¨¨ à §¢¨â¨¥ ¯à®æ¥áá ¯®©¤¥â ¯® ª®- ªà¥â®© âà ¥ªâ®à¨¨, ®¤ ª® ¯®«ã祮¥ à¥è¥¨¥ ¡ã¤¥â ᨫì- ® § ¢¨á¥âì ®â ç «ìëå ãá«®¢¨©, ¯®£à¥è®á⥩, ¢®§¬ãé¥- ¨©. ¤¥áì ¬ë ®¡à é ¥¬ ¢¨¬ ¨¥ ¢®§¨ª î騥 ⥮à¥â¨- ç¥áª¨¥ § âà㤥¨ï.
10.3.6. ª®«ì§ï騥 ०¨¬ë
¦л¬ ª« бᮬ ¥«¨¥©ле б¨бв¥¬ б а §ал¢®© ¯а ¢®© з - бвмо п¢«повбп б¨бв¥¬л, ¤«п ª®в®але б¢®©бв¢¥® бгй¥бв¢®- ¢ ¨¥ ᪮«ì§ïé¨å ०¨¬®¢ { ¤¢¨¦¥¨ï ¨§®¡à ¦ î饩 â®çª¨ ¯® ¯®¢¥àå®áâ¨ à §àë¢ , ¢ë§¢ ®¥ ⥬, çâ® ¢¥ªâ®àë ä §®¢®© ᪮à®á⨠¯à ¢«¥ë ®â®á¨â¥«ì® í⮩ ¯®¢¥àå®á⨠¢ ¯à®- ⨢®¯®«®¦ë¥ ®¡« áâ¨. १ã«ìâ ⥠¨§®¡à ¦ îé ï â®çª ¤¢¨¦¥âáï ¯® ¯®¢¥àå®áâ¨ à §àë¢ , ¯à¨ç¥¬ ¢¥ªâ®à ä §®¢®© ᪮à®á⨠¥ ¬®¦¥â ¡ëâì ®¯à¥¤¥«¥ ¯® ãà ¢¥¨ï¬ á¨áâ¥¬ë ¨ ¤«ï ®¤®© ¨§ ®¡« á⥩. ®§¨ª®¢¥¨¥ ᪮«ì§ï饣® à¥- ¦¨¬ ªà¨¢®©, § ¤ ®© ãà ¢¥¨¥¬ (x) = 0 ¯®ª § ® à¨á. 10.4, ¡. ª ¢¨¤® ¨§ à¨á㪠, ¢¥ªâ®àë ä §®¢®© ᪮à®-
á⨠¢¡«¨§¨ £à ¨æë à §àë¢ ¯à ¢«¥ë ¢ ¯à®â¨¢®¯®«®¦ë¥ ®¡« áâ¨. â® ¯à¨¢®¤¨â ª ⮬ã, çâ® ¨§®¡à ¦ îé ï â®çª § ª®¥ç®¥ ¢à¥¬ï ¯®¯ ¤ ¥â ªà¨¢ãî (x) = 0 ¨ ¤ «¥¥ ¤¢¨¦¥â- áï ¯® ¥©. ¤¥áì â ª¦¥ ¡«î¤ ¥âáï ¯¥à¥á¥ç¥¨¥ à §«¨çëå ä §®¢ëå âà ¥ªâ®à¨©.
®§¨ª ¥â § ¤ ç ®¯à¥¤¥«¥¨ï ¤¢¨¦¥¨ï á¨áâ¥¬ë ¯® 㪠- § ®© ¯®¢¥àå®áâ¨, ¤à㣨¬¨ á«®¢ ¬¨ { ®¯à¥¤¥«¥¨ï à¥è¥-
239

¨á. 10.4. ¥à¥á¥ª î騥áï âà ¥ªâ®à¨¨ ¨ ᪮«ì§ï騩 ०¨¬
¨ï ãà ¢¥¨ï (10.12), ¥á«¨ äãªæ¨ï f (x) ¯à¥â¥à¯¥¢ ¥â à §- àë¢ (¯® x) ¢ ª ¦¤ë© ¬®¬¥â ¢à¥¬¥¨. §¢¥á⥠àï¤ ¯®¤å®- ¤®¢ ª à¥è¥¨î í⮩ § ¤ ç¨ (á¬. [30, 102]). ¥ª®â®àë¥ ¨§ ¨å
¡ã¤ãâ à áᬮâà¥ë ¢ ¯. 11.6.
10.3.7. «¨ï¨¥ ¢¥è¨å ¢®§¤¥©á⢨©
«п ¥«¨¥©ле ¥бв ж¨® але б¨бв¥¬, б¨бв¥¬ ¯®¤¢¥а¦¥- ле ¢¥и¨¬ ¢®§¤¥©бв¢¨п¬, е а ªв¥а ¯®¢¥¤¥¨п бв ®¢¨вбп ¥й¥ ¡®«¥¥ б«®¦л¬. ª ®в¬¥з¥® ¢ли¥, ¢ ¥«¨¥©®¬ б«г- з ¥ ®вбгвбв¢г¥в б¢®©бв¢® а §¤¥«¥¨п, ¯®нв®¬г ª ª гбв®©з¨- ¢®бвм, в ª ¨ ª з¥бв¢® ¯а®ж¥бб®¢ ¢ в ª¨е б¨бв¥¬ е б«¥¤г¥в ¨§-
ãç âì, ¢®®¡é¥ £®¢®àï, á ãç¥â®¬ ®¤®¢à¥¬¥® ª ª ç «ìëå ãá«®¢¨©, â ª ¨ ¢¥è¨å ¢®§¤¥©á⢨©.
ਠ¢¥è¨å ¢®§¤¥©á⢨ïå ¬®£ãâ ¢®§¨ª âì â ª¨¥ ¥¨ï, ª ª ¯®¤ ¢«¥¨¥ ¨ ¢®§¡ã¦¤¥¨¥ ¢â®ª®«¥¡ ¨© (¢ § ¢¨á¨¬®á⨠®â ¢å®¤®£® ¯à®æ¥áá ), ¯à¨ã¤¨â¥«ì ï á¨åந§ æ¨ï ª®«¥- ¡ ¨©, ०¨¬ ¡¨¥¨©, ¥¨¥ ᪠窮®¡à §®£® ¨ ¯ à ¬¥âà¨-
ç¥áª®£® १® á , ¢®§¨ª®¢¥¨¥ å ®â¨ç¥áª¨å ¯à®æ¥áᮢ ¨ â.¤. [15, 72, 76].
ªâã «ìë¬ ï¢«ï¥âáï ¢®¯à®á ¨§ãç¥¨ï ¢«¨ï¨ï ¥«¨¥©- ëå §¢¥ì¥¢ ᢮©á⢠á¨á⥬ë, ¤«ï ª®â®à®© ¢ ®á®¢®¬ ¯à¨¬¥¨¬® «¨¥©®¥ ®¯¨á ¨¥. ¤¥áì ¬®£ãâ ¡ëâì á ¬ë¥ à §- ®®¡à §ë¥ á¨âã 樨. áâ ®¢¨¬áï «¨èì ¥ª®â®àëå.
ਠ«¨ç¨¨ ¥çã¢á⢨⥫ì®á⨠¤ â稪®¢ á¨á⥬ ã¯à -
240
¢«¥¨ï ¯à¥¦¤¥ ¢á¥£® ¯ ¤ ¥â â®ç®áâì á¨á⥬ë. ஬¥ â®- £®, ¤«ï áâ â¨ç¥áª¨ ¥ãá⮩稢ëå ®¡ê¥ªâ®¢ ã¯à ¢«¥¨ï ¨§-§ ¢ë§¢ ®£® ¥çã¢á⢨⥫ì®áâìî 㬥ìè¥¨ï ª®íää¨æ¨¥â ¯¥à¥¤ ç¨ ¯à¨ ¬ «ëå ®âª«®¥¨ïå á®áâ®ï¨¥ à ¢®¢¥á¨ï áâ - ®¢¨âáï ¥ãá⮩稢ë¬. â® ¬®¦¥â ¯à¨¢¥á⨠ª ¢â®ª®«¥¡ - ⥫쮬ã (¨«¨ ¤ ¦¥ à á室ï饬ãáï) ¯à®æ¥ááã [113]. «®- £¨ç®¥ ¢«¨ï¨¥ ®ª §ë¢ ¥â ª¢ ⮢ ¨¥ ᨣ «®¢ ¯® ãà®¢î ¢ á¨á⥬ å á æ¨ä஢묨 ॣã«ïâ®à ¬¨ [15, 76].
«¨ï¨¥ áëé¥¨ï «®£¨ç® 㬥ìè¥¨î ª®íää¨æ¨¥- â ãᨫ¥¨ï ¤«ï ᨣ «®¢ ¡®«ì让 ¬¯«¨âã¤ë. ᫨ ¤«ï ¡- ᮫îâ® ãá⮩稢ëå á¨á⥬ íâ® ¯à¨¢®¤¨â ª ¯®â¥à¥ â®ç®áâ¨, â® ¤«ï ãá«®¢® ãá⮩稢ëå á¨á⥬ áë饨¥ ¬®¦¥â ¯à¨¢¥- á⨠ª ¥ãá⮩稢®áâ¨. ஬¥ ⮣®, ¯à¨ áë饨¨ ᨣ « ã¯à ¢«¥¨ï ¤®«ï ¤¥¬¯ä¨àãîé¨å á®áâ ¢«ïîé¨å ¢ ã¯à ¢«ïî- 饬 ¢®§¤¥©á⢨¨ 㬥ìè ¥âáï, çâ® â ª¦¥ ¬®¦¥â ¯à¨¢¥á⨠ª ¥¦¥« ⥫ìë¬ á â®çª¨ §à¥¨ï ãá⮩稢®á⨠á¨á⥬ë ¥- ¨ï¬ [113].
¥«¥©ë¥ (à §àë¢ë¥) å à ªâ¥à¨á⨪¨ ¯à¨ ¬ «ëå ®âª«®- ¥¨ïå ¢å®¤®£® ᨣ « ¯à®ï¢«ïîâ á¥¡ï ª ª §¢¥ìï á ¡®«ì- 訬 ª®íää¨æ¨¥â®¬ ãᨫ¥¨ï. â® ¯à¨¢®¤¨â ª ¯®¢ë襨î
â®ç®áâ¨, ®¤ ª® ¬®¦¥â ¢ë§¢ âì ¥¦¥« ⥫ìë¥ ¢â®ª®«¥¡ - ¨ï ¨«¨ àã襨¥ ãá⮩稢®á⨠á¨á⥬ë [76, 94, 102, 106].
241
