
Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления
.pdf
¯ à ¬¥â஢ ®¡ê¥ªâ ¢¬¥áâ® (12.76) á«¥¤ã¥â ¨á¯®«ì§®¢ âì - áâà ¨¢ ¥¬ë© ¯à¥-䨫ìâà, § ¤ ¢ ¥¬ë© ãà ¢¥¨ï¬¨
xf (t) = Af xf (t) + Bf r(t) yf (t) = T (t)xf (t) |
(12.77) |
|||||||||||
£¤¥ xf (t) |
2 R |
N |
\ (t) |
2 R |
N { ¢¥ªâ®à áâà ¨¢ ¥¬ëå ¯ à ¬¥- |
|||||||
|
|
|
|
T |
|
|
N = n + n0. âà¨æë |
|||||
â஢: (t) = [!1(t) !2 |
(t) : : : !N (t)] |
|
|
|
||||||||
Af Bf § ¯¨è¥¬ ¢ ª ®¨ç¥áª®© ä®à¬¥ ä §®¢®© ¯¥à¥¬¥®© |
||||||||||||
( , á. 74). |
®¬¨ «ì®¥ § 票¥ (t) § ¢¨á¨â ®â |
|||||||||||
¯ à ¬¥â஢ ®¡ê¥ªâ ¨ ¤®«¦® 㤮¢«¥â¢®àïâì (12.76) ¤«ï ¯¥- |
||||||||||||
। â®ç®© äãªæ¨¨ |
Wf (s) = T (sI |
; |
Af );1Bf : ¢ë¡à ®¬ |
|||||||||
|
|
|
|
|
|
|
|
N |
|
|
||
ª ®¨ç¥áª®¬ ¡ §¨á¥ ¢ë¯®«¥® F (s) = |
|
i=1 |
! sN;i |
. âáî- |
||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
¤ ¯®«ãç ¥¬ á¨á⥬㠫¨¥©ëå ãà ¢¥¨© ¤«ï ®¬¨ «ìëå |
||||||||||||
§ 票©: ! |
i = 1 : : : N |
|
|
|
|
P |
|
|
|
|||
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
X |
!i sN;i |
= K(A(s)B0(s) + A0 |
(s)B(s)): |
(12.78) |
|||||||
|
|
|
||||||||||
i=1
⨠§ ç¥¨ï § ¢¨áï⠮⠥¨§¢¥áâëå ¯ à ¬¥â஢ ®¡ê¥ªâ , ®æ¥ª¨ ª®â®àëå ¬®£ãâ ¡ëâì ¯®«ãç¥ë á ¯®¬®éìî «£®à¨â¬ ¤ ¯â¨¢®© ¨¤¥â¨ä¨ª 樨, ®¯¨á ®£® ¢ 12.7.2.
«п ¢л¡®а игв ¢¢¥¤¥¬ б«¥¤гойго ¯¥а¥¤ в®зго дгª- ж¨о [107]:
|
Wc(s) = " ("s + 1)k;2 |
|
> 0: |
(12.79) |
|
(s + )k;1 |
|
|
|
¨¦¥ |
áä®à¬ã«¨à®¢ ë ᢮©á⢠|
|
à áè¨à¥®£® ®¡ê¥ªâ |
|
(12.74) á |
èã⮬ (12.79) [107]. |
|
|
|
1. ãáâì Wp (s) (12.72) { ¬¨¨¬ «ì®-ä §®¢ ï (B(s) {
£ãࢨ楢 ¬®£®ç«¥), ¨¬¥¥â ®â®á¨â¥«ìë© ¯®à冷ª k > 1 ¨ Wp (0) > 0: ®£¤ áãé¥áâ¢ãîâ ¯ à ¬¥âà 0 > 0 ¨ äãªæ¨ï "0( ) > 0 â ª ï, çâ® ¯¥à¥¤ â®ç ï äãªæ¨ï W (s) = Wp (s) + Wc (s) { áâண® ¬¨¨¬ «ì®-ä §®¢ ï ( ) ¤«ï ¢á¥å ¨ 0 < " < "0( 0).
2. ãáâì Wp (s) { ãá⮩稢 ï (A(s) { £ãࢨ楢 ¬®£®-
ç«¥), ¨¬¥¥â ®â®á¨â¥«ìë© ¯®à冷ª k > 1 ¨ Wp(0) > 0: ®£¤ ¤«ï «î¡®£® " > 0 áãé¥áâ¢ã¥â ¤®áâ â®ç® ¡®«ì讥 § 票¥0 â ª®¥, çâ® W (s) = Wp(s) + Wc(s) { ¤«ï ¢á¥å 0.
ª¨¬ ®¡à §®¬, ¬®¦® ¢¢¥á⨠èãâ (12.79) ¯®à浪
342

deg(As(s)) = k ; 1 = n ; m ; 1, ª®â®àë© ¯à¨ ¤®áâ â®ç® ¡®«ì- 讬 ¨ ¬ «®¬ " ®¡¥á¯¥ç¨¢ ¥â ãá«®¢¨¥ ¤«ï à áè¨à¥- ®£® ®¡ê¥ªâ (12.74) ¯à¨ «î¡®¬ ¬¨¨¬ «ì®-ä §®¢®¬ ®¡ê¥ªâ¥ ã¯à ¢«¥¨ï ¨ ¯à®¨§¢®«ì®© § ¤ ®© ®¡« á⨠¯ à ¬¥â஢.
ª á«¥¤ã¥â ¨§ ã⢥ত¥¨ï 2, ¯à¨ ¤à㣮¬ ᯮᮡ¥ ¢ë¡®- à ¯ à ¬¥â஢ èãâ (12.79), ãá«®¢¨¥ ¢ë¯®«ï¥âáï ¤«ï ãá⮩稢ëå (¨, ¢®§¬®¦®, ¥¬¨¨¬ «ì®-ä §®¢ëå) ®¡ê¥ªâ®¢.í⮬ á«ãç ¥ ãà ¢¥¨¥ èãâ ¬®¦® ã¯à®áâ¨âì\ ¨¬¥® ¢¬¥áâ® (12.79) ¬®¦® ¢§ïâì Wc (s) = s + :
।¯®«®¦¨¬ ⥯¥àì, çâ® èãâ (12.79) ¢ë¡à ¤«¥¦ - 騬 ®¡à §®¬ ¨ à áè¨à¥ë© ®¡ê¥ªâ (12.74) 㤮¢«¥â¢®àï¥â ãá«®¢¨î . ¥à¥¯¨è¥¬ ãà ¢¥¨ï à áè¨à¥®£® ®¡ê¥ª- â ¢ á«¥¤ãî饩 ª ®¨ç¥áª®© ä®à¬¥ [102, 189]:
|
x1(t) = A11x1(t) + A12x2(t) |
|
||
|
x2(t) |
= A21x1(t) + A22x2(t) + bu(t) |
(12.80) |
|
|
y(t) |
= Cx(t) |
|
|
£¤¥ x1 |
(t) 2 RN;1, x2 |
(t) 2 R |
¨ y(t) = c1x1(t) + c2x2 |
(t) { ¨§¬¥àï- |
¥¬ë© ¢ë室, c2b > |
0\ A11 |
xA12 A21 A22 b { ¥¨§¢¥áâë¥ |
||
¯ à ¬¥âàë, C = [c1 c2] : |
|
|
||
ª¨¬ ®¡à §®¬, ¢ à áᬠâਢ ¥¬®© § ¤ ç¥ âॡã¥âáï ©-
⨠ã¯à ¢«ïî饥 ¢®§¤¥©á⢨¥ u(t) ¨ § ª® áâனª¨ (t) ¢ (12.77) â ª®©, çâ® ¤«ï «î¡®£® ¤ ®£® § ç¥¨ï ®â®á¨â¥«ì- ®£® ¯®à浪 k ®¡ê¥ªâ ã¯à ¢«¥¨ï, ¥£® ¢ë室 ᨬ¯â®â¨ç¥- ᪨ 㤮¢«¥â¢®àï¥â (12.73).
¤ ç ¬®¦¥â ¡ëâì à¥è¥ ¢ ¤¢ íâ ¯ . ¥à¢ë© íâ ¯ á®á- ⮨⠢ à §à ¡®âª¥ «£®à¨â¬ ¨¤¥â¨ä¨ª 樨 ¯ à ¬¥â஢ ¨ ®¡¥á¯¥ç¥¨¨ ¨å á室¨¬®á⨠ª ¨áâ¨ë¬ § 票ï¬.
â®à®© íâ ¯ á®á⮨⠢ ¢ë¡®à¥ ã¯à ¢«¥¨ï u(t), ®¡¥á¯¥ç¨- ¢ î饣® á室¨¬®áâì (t) = y(t) ; yf (t) ª ã«î § ª®¥ç®¥ ¢à¥¬ï.
12.7.2. «£®à¨â¬ áâனª¨ ¯ à ¬¥â஢
¤ ®¬ ¯ à £à ä¥ ¯à¥¤áâ ¢«¥ «£®à¨â¬ ¨¤¥â¨ä¨ª 樨, ¡«¨§ª¨© ª ४ãàà¥â®© ¯à®æ¥¤ãॠ¬¥â®¤ ¨¬¥ìè¨å ª¢ - ¤à ⮢ ¨ ¨á¯®«ì§ãî騩 ⮫쪮 ¨§¬¥à¥¨ï ¢å®¤ ¨ ¢ë室 ®¡ê¥ªâ . ¥à¢ë¬ è £®¬ ï¥âáï à §à ¡®âª 䨫ìâ஢, ¢¢¥- ¤¥¨¥ ª®â®àëå ¯®§¢®«ï¥â ¨§¡¥¦ âì ¨§¬¥à¥¨ï ¯à®¨§¢®¤ëå ®â ¢ë室 ®¡ê¥ªâ .
343

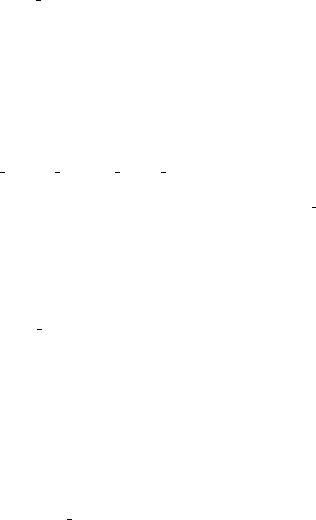
£¤¥ k0I > ;(0) = ;(0) |
T |
> 0 |
ç¥à¥§ (t) ®¡®§ ç¥ |
y~ |
(t). |
|
|||||
|
|
|
~ |
(n) |
|
®ª § ⥫ìá⢮ á室¨¬®á⨠¯ à ¬¥â஢ '~(t) ¨á¯®«ì§ã¥â ¯à¥¤¯®«®¦¥¨¥, çâ® á¨á⥬ ¯®¤¢¥à¦¥ ¥¨á祧 î饬㠢®§-
¡ã¦¤¥¨î á® áâ®à®ë ᨣ « ã¯à ¢«¥¨ï u(t) . |
|
|||||
«¨â¥à âãॠ®¯¨á ë ¨ ¤à㣨¥ |
«£®à¨â¬ë ¨¤¥â¨ä¨ª - |
|||||
樨, ®á®¢ ë¥ ¥ ¬¥â®¤¥ ¨¬¥ìè¨å ª¢ ¤à ⮢. |
¯à¨- |
|||||
¬¥à, [23, 106], ¬®¦® ¨á¯®«ì§®¢ âì |
«£®à¨â¬ |
|
||||
_ |
T |
(t) |
T |
|
~ |
(12.86) |
(t) = |
;;(t)'~(t)'~T |
|
(t) + ;(t)'~(t) (t) |
|||
;(t) = |
;;(t)'~(t)'~ |
(t);(t) + ;(t) |
|
|||
£¤¥ > 0 { ¯ à ¬¥âà «£®à¨â¬ . |
|
|
|
|||
«¥¤ãî騬 è £®¬ ï¥âáï ¢ë¡®à § ª® ã¯à ¢«¥¨ï.
12.7.3. ë¡®à § ª® ã¯à ¢«¥¨ï
®«ã稬 § ª® ã¯à ¢«¥¨ï, ®¡¥á¯¥ç¨¢ î騩 ᪮«ì§ï騩 à¥- ¦¨¬ ¯®¢¥àå®á⨠= y ; yf = 0. «ï í⮣®, ¨á¯®«ì§ãï (12.80), ¯à¥¤áâ ¢¨¬ ãà ¢¥¨¥ ®è¨¡ª¨ ¢ ¢¨¤¥
(t) = c1x1(t) + c2x2(t) ; yf (t) = |
|
|
|
||||
= c1A11x1(t)+ |
|
|
|
||||
+c1A12x2(t) + c2A21x1 (t) + c2A22x2(t) + c2bu(t) ; yf (t): |
|||||||
ਨ¬ ï ¢® ¢¨¬ ¨¥, çâ® |
|
|
|
|
|||
1 |
|
( (t) + yf (t) ; c1x1(t)) |
|
(12.87) |
|||
x2 (t) = |
|
|
|
||||
c2 |
|
||||||
¯®á«¥ ¯®¤áâ ®¢ª¨ (12.87) ¢ (12.87) ¯®«ã稬 |
|
|
|||||
(c2b);1 (t)=Lx1(t)+a1 (t)+a1yf (t);(c2 b);1y_f (t)+u(t) (12.88) |
|||||||
£¤¥ L { 1 (N ; 1)-¢¥ªâ®à\ |
|
22 c1 |
|||||
|
|
|
|
c A |
+ c A |
||
L = (c2b);1 c1A11 + c2A21 ; 1 |
12 c2 2 |
||||||
1 |
|
|
|
|
|||
a1 = |
|
(c1A12 + c2A22 ): |
|
|
|||
c2(c2b) |
|
|
|||||
।áâ ¢¨¬ ⥯¥àì ¬®¤¥«ì ®è¨¡ª¨ ¤«ï x1 (t). |
|
®¤áâ ¢«ïï |
|||||
(12.87) ¢ (12.80), ¯®«ã稬 |
|
|
|
|
|||
|
|
|
|
A12 |
A12 |
|
|
x1(t) = A x1(t) ; c2 (t) + |
c2 yf (t) |
(12.89) |
|||||
345 |
|
|
|
||||
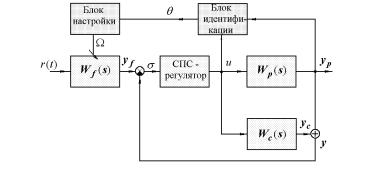
£¤¥ A = A11 |
; A12 |
c1 |
: à ¢¥¨ï (12.77), (12.88), (12.89) ®¯¨áë- |
|||
c2 |
||||||
¢ îâ ¬®¤¥«ì ®è¨¡ª¨. ç⥬, çâ® à áè¨à¥ë© ®¡ê¥ªâ ®¡« - |
||||||
¤ ¥â ᢮©á⢮¬ . â® ®§ ç ¥â [191], çâ® A { £ãࢨæ¥- |
||||||
¢ ¬ âà¨æ |
|
¨ c2b > 0: ¦® ®â¬¥â¨âì, çâ® yf (t) ®£à ¨ç¥® |
||||
(jyf (t)j |
|
f ) ¢á«¥¤á⢨¥ £ãࢨ楢®á⨠Af ¨ ®£à ¨ç¥®á⨠|
||||
y |
||||||
r(t), f (t). |
|
|
|
|
||
롥६ ⥯¥àì ᨣ « ã¯à ¢«¥¨ï ¢ ¢¨¤¥ |
|
|||||
|
|
|
u(t) = ;ks (t) ; sign( (t)) |
(12.90) |
||
£¤¥ ks ¨ { ¯®«®¦¨â¥«ìë¥ ¯ à ¬¥âàë. ¯à ¢«¥¨¥ (12.90) ®¡¥á¯¥ç¨¢ ¥â áãé¥á⢮¢ ¨¥ ã á¨á⥬ë ãá⮩稢®£® ᪮«ì- §ï饣® ०¨¬ ¯®¢¥àå®á⨠= 0: ¬¥â¨¬, çâ® ãá⮩ç¨- ¢®áâì á¨áâ¥¬ë ¬®¦¥â ¡ëâì ®¡®á®¢ ¯ã⥬ ¯®á«¥¤®¢ ⥫ì- ®£® ¯à¨¬¥¥¨ï ¤¢ãå äãªæ¨© ï¯ã®¢ [191]:
V |
= |
1 |
(cb);1 2 |
+ |
1xT |
P x |
V |
|
= |
1 |
(cb);1 2: |
|
1 |
|
2 |
|
|
2 |
1 |
1 |
|
2 |
|
2 |
|
¨á. 12.8. âàãªâãà ï á奬 ¤ ¯â¨¢®© á¨á⥬ë.
âàãªâãà ï á奬 ¤ ¯â¨¢®© á¨á⥬ë ã¯à ¢«¥¨ï ¯à¥¤- áâ ¢«¥ à¨á. 12.8.
12.7.4.ਬ¥à. ¤ ¯â¨¢®¥ ã¯à ¢«¥¨¥ «¥â ⥫ìë¬ ¯-
¯à ⮬
ª ç¥á⢥ ¯à¨¬¥à ¯à¨¬¥¥¨ï ¯à¥¤«®¦¥®£® ¬¥â®¤ à á- ᬮâਬ § ¤ çã ã¯à ¢«¥¨ï ¤¢¨¦¥¨¥¬ «¥â ⥫쮣® ¯¯ - à â ( ) ¯® â £ ¦ã. ãáâì ¨¬¥¥â ¯®áâ®ïë¥, ¯à¨- ®à®-¥®¯à¥¤¥«¥ë¥ ¯ à ¬¥âàë, § ç¥¨ï ª®â®àëå «¥¦ â ¢
346

§ ¤ ®© ®£а ¨з¥®© ®¡« бв¨. ¬¥в¨¬, зв® ¯®¤®¡ п б¨- вг ж¨п ¬®¦¥в ¨¬¥вм ¬¥бв® ¯а¨ ¯®«¥в¥ а §«¨зле а¥¦¨¬ е, ª®£¤ ¢лб®в , бª®а®бвм ¨ £аг§ª ¨§¬¥повбп ¬¥¤«¥- ® ¯® ба ¢¥¨о б в¥¬¯®¬ г£«®¢ле ¤¢¨¦¥¨©. «п ®¯¨б ¨п ¤¨ ¬¨ª¨ г£«®¢®£® ¤¢¨¦¥¨п ¨б¯®«м§г¥¬ б«¥¤гой¨¥ «¨-
¥ ਧ®¢ ë¥ ãà ¢¥¨ï [23] (á¬. |
â |
ª¦¥ ¯.¯. |
1.4.2. á. |
29\ |
|||||||||||||
1.5.3. á. 41) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< |
(t) = !z (t) + ay (t) + ay¢ ¢ (t) |
|
|
|
|
|
|
|||||||||
|
!_ (t) = |
|
a |
(t) |
|
a!z |
! |
(t) |
|
a ¢ |
|
|
(t) |
|
|
|
|
|
8 |
; |
; |
; |
¢ |
|
(12.91) |
||||||||||
|
_z |
mz |
|
mz |
z |
|
mz |
|
|
|
|||||||
|
: |
#(t) = !z(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
£¤¥ #(t) |
!(t) { 㣮« ¨ 㣫®¢ ï ᪮à®áâì â £ ¦ , (t) { 㣮« |
||||||||||||||||
â ª¨, |
(t) { 㣮« ®âª«®¥¨ï àã«¥© ¢ëá®âë\ |
a |
a |
a! |
a |
||||||||||||
¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
mz |
! |
|
am¢z { ¯ а ¬¥вал . е § з¥¨п § ¢¨бпв ®в гª § ле ¢л- и¥ д ªв®а®¢ ¨ ¬®£гв ¨§¬¥пвмбп ¢ и¨а®ª¨е ¯а¥¤¥« е ¢ § ¢¨-
ᨬ®á⨠®â ¢ëá®âë ¨ ᪮à®á⨠¯®«¥â . ®çë¥ § ç¥¨ï ¯ - à ¬¥â஢ ¯à¨®à® ¥ ®¯à¥¤¥«¥ë. ।¯®« £ ¥¬ â ª¦¥, çâ® ¤¨ ¬¨ª®© ¨á¯®«¨â¥«ì®£® ®à£ ¬®¦® ¯à¥¥¡à¥çì ¨ áç¨- â âì, çâ® ã¯à ¢«¥¨¥¬ ï¥âáï ®âª«®¥¨¥ àã«¥© ¢ (t): ç¨- â ¥¬, çâ® ¤®áâ㯠¨§¬¥à¥¨î ⮫쪮 ॣ㫨à㥬 ï ª®®à¤¨- â #(t): à ¢¥¨ï¬ (12.91) ®â¢¥ç ¥â ¯¥à¥¤ â®ç ï äãªæ¨ï (12.72), £¤¥ deg A(s) = 3 deg B(s) = 1 k = 2 :
¤ ®© § ¤ ç¥ âॡã¥âáï ®¡¥á¯¥ç¨âì § ¤ ®¥ ¯®¢¥¤¥¨¥ ¢â®¯¨«®â¨à㥬®© á¨á⥬ë ã¯à ¢«¥¨ï ¢ ᮮ⢥âá⢨¨ á
íâ «®®© ¬®¤¥«ìî (12.73), £¤¥ Am(s) = p3 + am1 p2 + am2 p + am3 .®íää¨æ¨¥âë ãà ¢¥¨ï ®¡ê¥ªâ ã¯à ¢«¥¨ï (12.81) á¢ï-
§ ë á ¯ à ¬¥âà ¬¨ ¬®¤¥«¨ (12.91) á®®â®è¥¨ï¬¨
a1 = a!mzz ;ay a2 =amz ;a!mzz ay a3 =0 b0 =;am¢z b1 = am¢z ay + ay¢ amz :
祢¨¤®, çâ® §¤¥áì ¥ âॡã¥âáï ¯à®¢®¤¨âì ®æ¥¨¢ ¨ï a3 \ á«¥¤®¢ ⥫ì®, ¬®¦® 㬥ìè¨âì ç¨á«® ®æ¥¨¢ ¥¬ëå ¯ à - ¬¥â஢ ¨ ã¯à®áâ¨âì «£®à¨â¬ ¨¤¥â¨ä¨ª 樨.
à áᬠâਢ ¥¬®¬ ¯à¨¬¥à¥ ®â®á¨â¥«ìë© ¯®à冷ª ®¡ê-
¥ªâ k = 2 ¨ èãâ (12.79) ¬®¦¥â ¡ëâì § ¤ ¯¥à¥¤ â®ç®© |
|||||
äãªæ¨¥© Wc(s) = |
|
|
¨¬¥î饩 ¯ à ¬¥âàë > 0 > 0: |
||
s + |
|||||
|
|
|
|||
¢¥¤¥¬ 䨫ìâàë âà¥â쥣® ¯®à浪 ¤«ï ¢å®¤®£® ¨ ¢ë室- |
|||||
®£® ¯à®æ¥áᮢ (12.76) ¢ ¢¨¤¥ |
|
||||
x#(t) = Adx#(t) + bd#(t) |
x (t) = Adx (t) + bd ¢ (t) (12.92) |
||||
|
|
|
|
347 |
|

£¤¥ x#(t) x (t) |
2R |
3 |
Ad |
bd ¨¬¥îâ ª ®¨ç¥áªãî ä®à¬ã ä - |
|||||||
|
|
|
|
3 |
2 |
+d2s+d3 |
: ¥ª- |
||||
§®¢®© ¯¥à¥¬¥®©, det(sI;Ad) D(s) = s |
|
+d1s |
|||||||||
â®à '~(t) ⥯¥àì ¬®¦® § ¯¨á âì ¢ ¢¨¤¥ '~(t) = [x# 3(t) x# 2(t) |
|||||||||||
x 2(t) x 1 (t)]T : ¨£ « ~(t) ¢ (12.84) ®¯à¥¤¥«ï¥âáï ¢ëà ¦¥¨¥¬ |
|||||||||||
x# 3(t) ¨ ¬®¦¥â ¡ëâì ©¤¥ ¨§ (12.92) ç¥à¥§ x#(t) #(t) ¡¥§ ¤¨ä- |
|||||||||||
ä¥à¥æ¨à®¢ ¨ï. ®¬¯®¥â ¬¨ ¢¥ªâ®à |
|
(t) 2 R4 п¢«повбп |
|||||||||
®æ¥ª¨ ᮮ⢥âáâ¢ãîé¨å ¯ à ¬¥â஢ ¯¥à¥¤ â®ç®© äãªæ¨¨ |
|||||||||||
;a1 ;a2 b0 |
b1 |
: ¤ ®¬ ¯à¨¬¥à¥ ;(t) { ¬ âà¨æ |
4 |
|
4, |
||||||
|
|||||||||||
;(0) = k0I: ª®ç â¥«ì® |
«£®à¨â¬ ¨¤¥â¨ä¨ª 樨 ¨¬¥¥â ¢¨¤ |
||||||||||
(12.84), (12.85): |
|
|
|
|
|
|
|
|
|
|
|
t t ' t ' t t t ' t t
_( ) = ;;( ) ~( ) ~T ( ) T ( ) + ;( ) ~( )~( )
;(t) = ;;(t)'~(t)'~T (t);(t) + ;(t) ; k10 ;2(t) : (12.93)
áᬮâਬ ⥯¥àì ॣã«ïâ®à á ¯¥à¥¬¥®© áâàãªâãன.¢¥¤¥¬ à áè¨à¥ë© ¢ë室®© ᨣ « ya (t) = #(t)+yc(t) £¤¥ yc(t) { ¢ë室 èãâ¨àãî饣® §¢¥ ¨ ¢ë¡¥à¥¬ ᨣ « ã¯à ¢«¥- ¨ï ¢ ¢¨¤¥
¢(t) = ;ks (t) ; sign (t) |
(12.94) |
£¤¥ (t) = y(t) ; yf (t)\ yf (t) { ¢ë室 ¯à¥-䨫ìâà |
(12.77). |
«ï ¤®á⨦¥¨ï 楫¨ ã¯à ¢«¥¨ï (12.73) ©¤¥¬ ¯ à ¬¥-
âàë ¯à¥-䨫ìâà â ª, çâ®¡ë ¯à¨ ¢ë¯®«¥¨¨ ¯à¥¤¯®«®¦¥- ¨ï ® á室¨¬®á⨠®æ¥®ª ¯ à ¬¥â஢ ¢ ãáâ ®¢¨¢è¥¬-
áï ०¨¬¥ ª ¨å ¨áâ¨ë¬ § ç¥¨ï¬ ãà ¢¥¨ï ¯à¥-䨫ìâà |
|
(12.77) 㤮¢«¥â¢®à﫨 (12.76), £¤¥ |
K = Am(0) ¨ ¬®£®ç«¥ |
|
B(0) |
F (s) = Ap(s)B0(s) + A0(s)Bp(s) : «ï ¤ ®© á¨áâ¥¬ë ¯®«ãç ¥¬ |
|
F (s) = s3 + ( a1 + b0)s2 + ( a2 |
+ b0 + b1)s + b1 (12.95) |
¨ § ¬¥ â¥«ì ¯¥à¥¤ â®ç®© äãªæ¨¨ Wf (s) (12.76) { ¬®£®- ç«¥ ç¥â¢¥à⮩ á⥯¥¨:
Am(s)A0(s) = s4 + ( + d1)s3 + ( d1 + d2)s2 + ( d2 + d3)s + d3 :ª®ç â¥«ì® ¯®«ãç ¥¬ á«¥¤ãî騥 ãà ¢¥¨ï áâà ¨¢ ¥-
348

¬®£® ¯à¥-䨫ìâà |
(12.77): |
|
|
|||
xf 1(t) = xf 2(t) xf 2(t) = xf 3(t) |
|
|
||||
xf 3(t) = xf 4(t) |
|
|
||||
xf 4(t) = ; d3xf 1(t) ; d3xf 2(t) ; ( d1 + d2)xf 3(t); |
||||||
; |
( + d1)xf 4(t) + r(t) |
|
|
|||
|
|
P |
4 |
; |
(12.96) |
|
yf (t) = K(t) |
i=1 !i(t)xf i(t) |
|||||
!1(t) = 4 (t) !2 (t) = 4(t) + 3(t) 2 (t) |
||||||
!3(t) = 3 (t) |
; 1(t) !4 = |
|
|
|||
K(t) = |
d3 |
: |
|
|
|
|
4 (t) |
|
|
|
|||
|
|
|
|
|
|
|
஢¥à¨¬ ⥯¥àì ¢ë¯®«¥¨¥ ãá«®¢¨ï ¤«ï à áᬠ-
âਢ ¥¬®© á¨á⥬ë. ¤ ®¬ á«ãç ¥ ç¨á«¨â¥«ì ¯¥à¥¤ â®ç- ®© äãªæ¨¨ à áè¨à¥®£® ®¡ê¥ªâ (12.74) F (s) ¨¬¥¥â ¢¨¤ (12.95) ¨ ¤®«¦¥ ¡ëâì £ãà¢¨æ¥¢ë¬ ¬®£®ç«¥®¬ âà¥â쥩 áâ¥- ¯¥¨. 㤥¬ à áᬠâਢ âì , ¨¬¥î騥 ®à¬ «ìãî íà®- ¤¨ ¬¨ç¥áªãî á奬ã [19, 23]. ਠí⮬ ª®íää¨æ¨¥âë ç¨á«¨-
â¥«ï ¯¥à¥¤ â®ç®© äãªæ¨¨ W ¢ ®âà¨æ ⥫ìë, b0 < 0 b1 < 0:
вбо¤ ¢лв¥ª ов б«¥¤гой¨¥ б®®в®и¥¨п, ª®в®ал¥ ¤®«¦л ¢л¯®«пвмбп ¤«п ¯ а ¬¥ва®¢ ¨ игв :
< 0 b0 + a1 |
< 0 b0 + a2 + b1 |
< 0 |
(12.97) |
|
b02 + a1b0 + 2a1a2 + b0b1 ; b1 > 0: |
||||
|
||||
ª ç¥á⢥ ¨««îáâà 樨 à áᬮâਬ १ã«ìâ âë ¨á¯®«ì- §®¢ ¨ï à áᬮâ८£® ¤ ¯â¨¢®£® ॣã«ïâ®à (12.94), (12.92),
(12.96), (12.79) á «£®à¨â¬®¬ ¨¤¥â¨ä¨ª 樨 (12.86) ¢ § ¤ - ç¥ ã¯à ¢«¥¨ï , ç¨á«¥ë¥ § ç¥¨ï ¯ à ¬¥â஢ ª®â®à®- £® ¤«ï à §«¨çëå ०¨¬®¢ ¯®«¥â ¯à¨¢¥¤¥ë ¢ â ¡«. 12.1.
ª ¢¨¤® ¨§ в ¡«¨жл, ¯ а ¬¥вал ¨§¬¥повбп ¢ и¨а®- ª¨е ¯а¥¤¥« е ¨ а¥¦¨¬ 3 б®®в¢¥вбв¢г¥в ¥гбв®©з¨¢®¬г ®¡к¥ª-
âã.
ਠ¬®¤¥«¨à®¢ ¨¨ ¯à¨ïâë á«¥¤ãî騥 § ç¥¨ï ¯ à - ¬¥â஢ «£®à¨â¬®¢ ã¯à ¢«¥¨ï ¨ ¨¤¥â¨ä¨ª 樨:
{ å à ªâ¥à¨áâ¨ç¥áª¨© ¬®£®ç«¥ íâ «®®© ¬®¤¥«¨
Am(s)=s3 +am1 s2 +am2 s+am3 am1 =14:2 c;1 am2 =51 c;2 am3 =90 c;3:
{ ¯ à ¬¥âàë èãâ¨àãî饣® §¢¥ : = 10 c;1 = |
|
2 \ |
|
|
||
{ ¯ à ¬¥âàë 䨫ìâ஢ (12.76): d1 = 20 c |
|
d2 = 200 c |
|
|||
|
;1 |
|
; |
|
;2 |
|
d3 = 103 c;3 \
349

¡«¨æ 12.1. à ¬¥âàë ¬®¤¥«¨
|
ay |
amz |
am!zz |
ay¢ |
am¢z |
a1 |
a2 |
b0 |
b1 |
|
|
|
|
|
|
|
|
|
|
N0 |
c;1 |
c;2 |
c;1 |
c;1 |
c;1 |
c;2 |
c;2 |
c;2 |
c;3 |
|
|
|
|
|
|
|
|
|
|
1 |
;1:10 |
15:5 |
1:20 |
0:09 |
33:0 |
2:3 |
16:8 |
;33 |
;35 |
2 |
;0:86 |
5:81 |
0:18 |
0:06 |
9:15 |
1:0 |
6:0 |
;9:2 |
;7:5 |
3 |
;1:34 |
;12:5 |
0:45 |
0:07 |
15:2 |
1:8 |
;12 |
;15:2 |
;21:2 |
{¯ à ¬¥âàë ॣã«ïâ®à á ¯¥à¥¬¥®© áâàãªâãன: ks = 10 = 3\
{ ç «ìë¥ § ç¥¨ï ¢ «£®à¨â¬¥ ¨¤¥â¨ä¨ª 樨:
;(0) = k0I k0 = 103 (0) = [0 0 0 ;10:] \ ¯ à ¬¥âà = 5\
¨á. 12.9. à ¨æ ®¡« á⨠¤«ï = 0:5.
¥à ¢¥á⢠(12.97) ®¯à¥¤¥«ïîâ ®¡« áâì à áè¨à¥- ®£® ®¡ê¥ªâ , â.¥. ¤¨ ¯ §® § 票© ¯ à ¬¥â஢ , ¤«ï ª®â®àëå ¯à¨¬¥¨¬ § ª® ã¯à ¢«¥¨ï (12.94). à¨á. 12.9 ¯®ª § ®¡« áâì "㦥áâ®ç¥®©" , ¤«ï ª®â®à®© ç¨á- «¨â¥«ì ¯¥à¥¤ â®ç®© äãªæ¨¨ à áè¨à¥®£® ®¡ê¥ªâ (12.74)
F (s) ¨¬¥¥â á⥯¥ì ãá⮩稢®á⨠= 0:5: 18 ਠ¯®áâ஥¨¨
18 ¯®¬¨¬, çâ® á⥯¥ìî ãá⮩稢®á⨠¬®£®ç«¥ á⥯¥¨ n §ë- ¢ ¥âáï ¢¥«¨ç¨ = ;maxi(Re si) i = 1 2 : : : n [15, 95, 76].
350

¨á. 12.10. à®æ¥áá ¨¤¥â¨ä¨ª 樨 ¯ à ¬¥â஢ .
¨á. 12.11. ¥à¥å®¤ë¥ ¯à®æ¥ááë ¯® 㣫ã â £ ¦ .
®¡« á⨠¢ àì¨à®¢ «¨áì ¯ à ¬¥âàë ay amz amz : à - ¬¥âàë ay¢ = 0:07 á;1 a!mzz = 0:18 á;2: ¨äà ¬¨ à¨á. 12.9 ®¡®§ ç¥ë â®çª¨, ᮮ⢥âáâ¢ãî騥 áâப ¬ â ¡«. 12.1.
¥§ã«ìâ âë ¬®¤¥«¨à®¢ ¨ï ¯à¨¢¥¤¥ë à¨á. 12.10, 12.11.¥à¥å®¤ë¥ ¯à®æ¥ááë ¯® 㣫ã â £ ¦ ¯à¨ § ¤ î饬 ¢®§-
¤¥©á⢨¨ r(t) # (t) ¢ ¢¨¤¥ ¯àאַ㣮«ì®© ¢®«ë
# (t) = #0sign(sin(0:2 t))
£¤¥ #0 = 5 £à ¤. ¤«ï à §«¨çëå § 票© ¯ à ¬¥â஢ ¨§ â - ¡«¨æë 12.1 ¯à¨¢¥¤¥ë à¨á. 12.10. à¨á. 12.11 ¯®ª § ë £à 䨪¨ ®æ¥®ª ¯ à ¬¥â஢ ¤«ï ०¨¬ 1 (á«¥¤ã¥â ®¡à -
351
