Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления

3)§­ ª b0 ¢ (13.43) ¨§¢¥á⥭\

4)¯ à ¬¥âàë á¨áâ¥¬ë ¨ 楫ì 㤮¢«¥â¢®àïîâ á«¥¤ãî騬 ®£à ­¨ç¥­¨ï¬:

®£¤ áãé¥áâ¢ã¥â 0 > 0 â ª®¥, çâ® ¤«ï ª ¦¤®£® y< 0 áãé¥áâ¢ãîâ > 0, >0, 2(0,1) â ª¨¥, ç⮠楫ì (13.40) á y ¨ y ¤«ï ¢á¥å ¤®áâ â®ç­® ¡®«ìè¨å k >0 ¢ á¨á⥬¥ (13.39), (13.45), (13.46) á ®£à ­¨ç¥­¨¥¬ jukj< u.

®ª § ⥫ìá⢮ â¥®à¥¬ë ®á­®¢ ­® ­ ¨á¯®«ì§®¢ ­¨¨ äã­ª- 樨 ï¯ã­®¢ V (x) = k ; k2. ëè¥ãª § ­­ë© «£®à¨â¬ ¡ë« ãᯥ譮 ¯à¨¬¥­¥­ ª § ¤ ç ¬ ¤ ¯â¨¢­®£® ã¯à ¢«¥­¨ï ¬®¤¥-

«ìî ¡àîáᥫïâ®à á ¢­¥è­¨¬ ¢®§¡ã¦¤¥­¨¥¬, ¬®¤¥«ìî ñá- á«¥à ¨ ¬®¤¥«ìî ãªã誨­ { ᨯ®¢ 娬¨ç¥áª®© ॠªæ¨¨ á ä §®¢ë¬ ¯¥à¥å®¤®¬ [31, 149].

¨¦¥ ¯à¨¢®¤ïâáï ¢ ª ç¥á⢥ ¯à¨¬¥à®¢ १ã«ìâ âë ¤«ï ¡àîáᥫïâ®à ¨ á¨á⥬ë ñáá«¥à , á«¥¤ãï [31].

13.4.2. ¤ ¯â¨¢­®¥ ã¯à ¢«¥­¨¥ ¬®¤¥«ìî ¡àîáᥫïâ®à

¤­®© ¨§ ­ ¨¡®«¥¥ ¯®¯ã«ïà­ëå ¨ ¯®¤à®¡­® ¨áá«¥¤®¢ ­­ëå ¬®¤¥«¥© 娬¨ç¥áª®© ª¨­¥â¨ª¨ ï¥âáï âਬ®«¥ªã«ïà­ ï ¬®- ¤¥«ì, ¨«¨ ¡àîáᥫïâ®à. â ¬®¤¥«ì ¡ë« ¯à¥¤«®¦¥­ . ìî- ਭ£®¬ [192] ¢ 1952£. ¨ ¤¥â «ì­® ¨§ãç « áì . ਣ®¦¨­ë¬ á

гбв®©з¨¢л© ¯а¥¤¥«м­л© ж¨ª« [70], ¯®¤®¡­л© ¨§®¡а ¦¥­­®¬г ­ а¨б. 13.2. бᬮва¨¬ б«¥¤гойго § ¤ зг г¯а ¢«¥­¨п.гбвм ¢ ¬®¬¥­вл ¢а¥¬¥­¨ tk ¯¥à¥¬¥­­ ï Y (t) ¤®á⨣ ¥â ᢮¥£®

382

¨á. 13.2. áâ®©ç¨¢ë© ¯à¥¤¥«ì­ë© 横« ¡àîáᥫïâ®à .

k-£® «®ª «ì­®£® ¬ ªá¨¬ã¬ , ᮮ⢥âáâ¢ãî饥 ¬ ªá¨¬ «ì­®¥ §­ 祭¨¥ ®¡®§­ 稬 yk = Y (tk ). ãáâì ã¯à ¢«ïî饥 ¢®§¤¥©- á⢨¥ u(t) ¡ã¤¥â ªãá®ç­®-¯®áâ®ï­­®© ä㭪樥©, ¨§¬¥­ïî饩 ¯ à ¬¥âà A ¢ ¬®¬¥­âë ¢à¥¬¥­¨ tk á ãç¥â®¬ ¨§¬¥à¥­­®£® §­ - 祭¨ï yk : A = A0 + u(t), u(t) = uk ¤«ï tk t < tk+1. ­ 祭¨ï ¯ à ¬¥â஢ á¨á⥬ë A0 ¨ B ¯à¥¤¯®« £ îâáï ­¥¨§¢¥áâ­ë¬¨.¥«ì ã¯à ¢«¥­¨ï á®á⮨⠢ 㤥ঠ­¨¨ §­ 祭¨© «®ª «ì­ëå ¬ ªá¨¬ã¬®¢ Y (t) ­ ¤ ­­®¬ ã஢­¥ y á ¯®¬®éìî 楫¥­ ¯à - ¢«¥­­®£® ¨§¬¥­¥­¨ï u(t) ¢ ¬®¬¥­âë ¢à¥¬¥­¨ tk. ¨­¥ ਧ®- ¢ ­­ ï ¬®¤¥«ì "¢å®¤{¢ë室" (13.43) ¯à¨¬¥â ¢¨¤

£¤¥ a ¨ b { ­¥¨§¢¥áâ­ë¥ ª®íää¨æ¨¥­âë, 'k { ®£à ­¨ç¥­­ ï ®è¨¡ª ¬®¤¥«¨.

®¯à¥¤¥«ïî騩 ­®¢®¥ §­ 祭¨¥ ã¯à ¢«ïî饣® ¢®§¤¥©á⢨ï uk , ¨ «£®à¨â¬ ¤ ¯â 樨, ®á­®¢ ­­ë© ­ १ã«ìâ â å ¯à¥¤ë- ¤ã饩 £« ¢ë ¨ ¢ëç¨á«ïî騩 ®æ¥­ª¨ ^ ^ ¯ à ¬¥â஢ ¬®¤¥«¨

ak bk

383

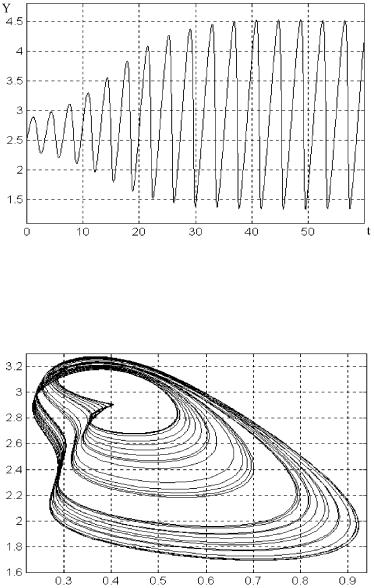
¨á. 13.3. à 䨪 Y (t) ¤«ï ã¯à ¢«ï¥¬®£® ¡àîáᥫïâ®à .

¨á. 13.4. ®â¨ç¥áª¨© ââà ªâ®à ¢®§¡ã¦¤¥­­®£® ¡àîáᥫï- â®à .

384

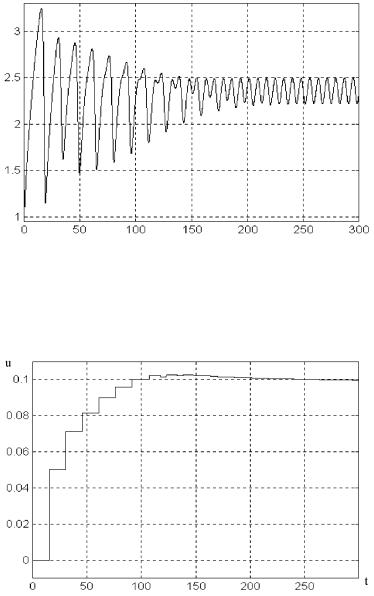
¨á. 13.5. à 䨪 Y (t) ¤«ï ã¯à ¢«ï¥¬®£® ¢®§¡ã¦¤¥­­®£® ¡àîáᥫïâ®à (y =2.5).

¨á. 13.6. à 䨪 u(t) ¤«ï ã¯à ¢«ï¥¬®£® ¢®§¡ã¦¤¥­­®£® ¡àîáᥫïâ®à (y =2.5).

385

楫¨ ã¯à ¢«¥­¨ï (13.40) ¯à¨ y = 4:5 ( max Y (t) 3:55 ¤«ï ­¥- ã¯à ¢«ï¥¬®© á¨á⥬ë). 뫨 ¢ë¡à ­ë á«¥¤ãî騥 ­ ç «ì-

13.4). ®áâ ­®¢ª § ¤ ç¨ ã¯à ¢«¥­¨ï ¨ ¤ ¯â¨¢­ë© «£®à¨â¬

г¯а ¢«¥­¨п ­¥ ¬¥­повбп ¢ ба ¢­¥­¨¨ б а бᬮва¥­­®© § ¤ - з¥© г¯а ¢«¥­¨п ª®«¥¡ ­¨п¬¨ ¡аобб¥«пв®а . н⮬ б«гз ¥ A = A0 + a~ cos(!t) + u(t), yk = Y (tk): ­ 祭¨ï ¯ à ¬¥â஢ á¨- á⥬ë A0 B a~ ¨ ! ¯à¥¤¯®« £ îâáï ­¥¨§¢¥áâ­ë¬¨. ¥«ì ã¯à - ¢«¥­¨ï á®á⮨⠢ 㤥ঠ­¨¨ §­ 祭¨© «®ª «ì­ëå ¬ ªá¨¬ã- ¬®¢ Y (t) ­ ¤ ­­®¬ ã஢­¥ y á ¯®¬®éìî 楫¥­ ¯à ¢«¥­­®£®

¨§¬¥­¥­¨ï u(t) ¢ ¬®¬¥­âë ¢à¥¬¥­¨ tk .

à¨á. 13.5, 13.6 ¯®ª § ­ë § ¢¨á¨¬®á⨠Y (t) ¨ u(t) ®â ¢à¥- ¬¥­¨ t ¯à¨ y =2.5 (maxY (t) 3:2 ¤«ï ­¥ã¯à ¢«ï¥¬®© á¨áâ¥- ¬ë). «ï ¬®¤¥«¨à®¢ ­¨ï ¡ë«¨ ¢ë¡à ­ë á«¥¤ãî騥 ­ ç «ì- ­ë¥ ãá«®¢¨ï ¨ §­ 祭¨ï ¯ à ¬¥â஢: X(0)=0.5\ Y (0)=1.0. ®- ¤¥«¨à®¢ ­¨¥ ¯®ª § «®, ç⮠楫ì ã¯à ¢«¥­¨ï (13.40) â ª¦¥ ¤®-

á⨣ ¥âáï ¤«ï ¤àã£¨å §­ 祭¨© y , ¢¯«®âì ¤® y =3.5.

13.4.3. ¤ ¯â¨¢­®¥ ã¯à ¢«¥­¨¥ ¬®¤¥«ìî ñáá«¥à

­ áâ®ï饩 £« ¢¥ ¬®¤¥«¨à®¢ ­¨¥¬ ¨áá«¥¤ã¥âáï ¢®¯à®á ® ­¥- ®¡å®¤¨¬®á⨠¢¢¥¤¥­¨ï ®£à ­¨ç¥­¨ï ­ ¢¥«¨ç¨­ã ã¯à ¢«¥­¨ï ¨ ¢®§¬®¦­®á⨠¤®á⨦¥­¨ï 楫¨ ã¯à ¢«¥­¨ï á ¯®¬®éìî â - ª®£® ®£à ­¨ç¥­¨ï ¯®á।á⢮¬ ¬ «®£® ã¯à ¢«¥­¨ï.

áᬮâਬ ¬®¤¥«ì ¤¨­ ¬¨ª¨ 娬¨ç¥áª®© ॠªæ¨¨, ¯à®â¥-

ªî饩 ¢ ­¥ª®â®à®© ¥¬ª®áâ¨ á ¯¥à¥¬¥è¨¢ ­¨¥¬ ¨ ¯à¥¤«®¦¥­-

386

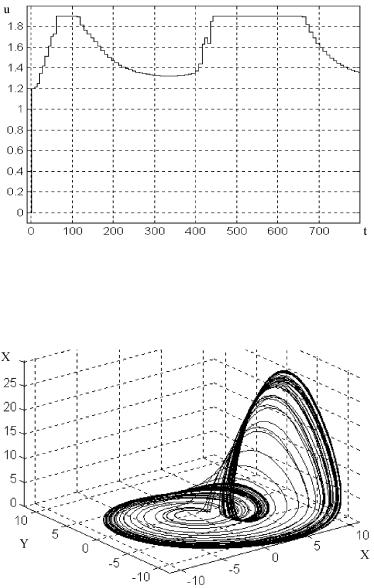
¨á. 13.9. à 䨪 ã¯à ¢«¥­¨ï u(t) (y = 6).

¨á. 13.10. §®¢ë© ¯®àâà¥â ã¯à ¢«ï¥¬®© ¬®¤¥«¨ ¥áá«¥à (y = 6).

388

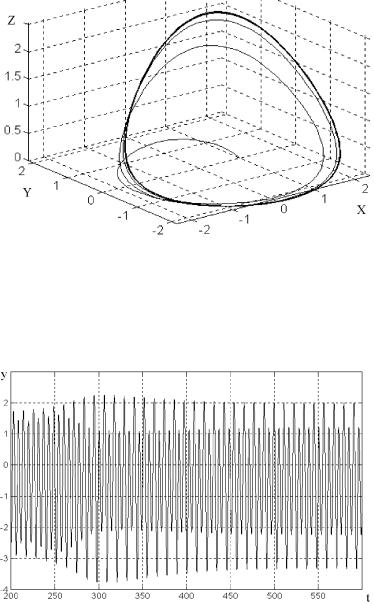
¨á. 13.11. ।¥«ì­ë© 横« ¯¥à¢®£® ¯®à浪 ¢ á¨á⥬¥¥áá«¥à .

¨á. 13.12. à 䨪 ª®®à¤¨­ âë Y (t) (y = 2).

389

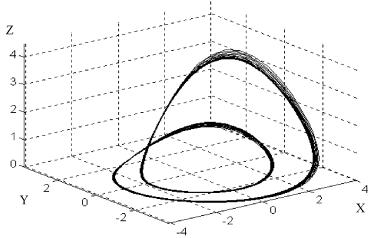
¨á. 13.13. §®¢ë© ¯®àâà¥â ã¯à ¢«ï¥¬®© ¬®¤¥«¨ ¥áá«¥à (y = 2).

­®© . ¥á᫥஬ ¢ 1976 £. [68, 70]:

£¤¥ A B C { ¯®«®¦¨â:¥«ì­ë¥ ¯ à ¬¥âàë. í⮩ ¬®¤¥«¨ ¨¬¥-

¥âáï ­¥ãá⮩稢®¥ ¯®«®¦¥­¨¥ à ¢­®¢¥á¨ï ¢ â®çª¥ X = Y = = Z = 0 ¨ ¯à¨ ­¥ª®â®àëå §­ 祭¨ïå ¯ à ¬¥â஢ A,B,C ¤¨­ -

¬¨ª á¨á⥬ë (13.53) áâ ­®¢¨âáï å ®â¨ç¥áª®© [70], ª ª ¯®ª -

§­® ­ à¨á. 13.7.

бᬮва¨¬ б«¥¤гойго § ¤ зг г¯а ¢«¥­¨п. гбвм tk { в¥ ¬®¬¥­вл ¢а¥¬¥­¨, ¢ ª®в®ал¥ ¯¥а¥¬¥­­ п Y (t) ¤®бв¨£ ¥в б¢®¥£® k-£® «®ª «м­®£® ¬ ªб¨¬г¬ . ®®в¢¥вбв¢гой¥¥ ¬ ªб¨- ¬ «м­®¥ §­ з¥­¨¥ ®¡®§­ з¨¬ yk =Y (tk). гбвм г¯а ¢«пой¥¥ ¢®§¤¥©бв¢¨¥ ¡г¤¥в ªгб®з­®-¯®бв®п­­®© дг­ªж¨¥©, ¨§¬¥­по-

饩 §­ 祭¨¥ ¯ à ¬¥âà C ¢ ¬®¬¥­âë tk á ãç¥â®¬ ¨§¬¥à¥­- ­®£® §­ 祭¨ï yk: C = C0 + u(t), u(t) = uk ¤«ï tk t < tk+1.­ 祭¨ï ¯ à ¬¥â஢ á¨á⥬ë A,B,C0 ¯à¥¤¯®« £ îâáï ­¥¨§- ¢¥áâ­ë¬¨. ¥«ì ã¯à ¢«¥­¨ï á®á⮨⠢ 㤥ঠ­¨¨ §­ 祭¨© «®ª «ì­ëå ¬ ªá¨¬ã¬®¢ Y (t) ­ ¤ ­­®¬ ã஢­¥ y á ¯®¬®éìî 楫¥­ ¯à ¢«¥­­®£® ¨§¬¥­¥­¨ï u(t) ¢ ¬®¬¥­âë ¢à¥¬¥­¨ tk . ¨-

390

­¥ ਧ®¢ ­­ ï ¬®¤¥«ì "¢å®¤{¢ë室" (13.43) ¤«ï à áᬠâà¨- ¢ ¥¬®© á¨áâ¥¬ë ¯à¨¬¥â ¢¨¤

yk+1 + a1yk + a2yk;1 + a3yk;2 = b1uk +b2uk;1 + b3uk;2 + 'k (13.54)

£¤¥ uk { ã¯à ¢«ïî饥 ¢®§¤¥©á⢨¥\ faig3 ¨ fbig3 { ­¥¨§¢¥áâ­ë¥

1 1

ª®íää¨æ¨¥­âë\ 'k { ®£à ­¨ç¥­­ ï ®è¨¡ª ¬®¤¥«¨.

¤ ¯â¨¢­ë© «£®à¨â¬ ã¯à ¢«¥­¨ï ¢ª«îç ¥â ¢ á¥¡ï «£®- à¨â¬ ã¯à ¢«¥­¨ï ®á­®¢­®£® ª®­âãà

®¯à¥¤¥«ïî騩 ­®¢®¥ §­ 祭¨¥ ã¯à ¢«ïî饣® ¢®§¤¥©á⢨ï uk , ¨ «£®à¨â¬ ¤ ¯â 樨, ®á­®¢ ­­ë© ­ १ã«ìâ â å ¯à¥- ¤ë¤ã饣® ¯ à £à ä ¨ ¢ëç¨á«ïî騩 ®æ¥­ª¨ ^ ^ ¯ à ¬¥-

ai k bi k

â஢ ¬®¤¥«¨ (13.54) ®¡ê¥ªâ ã¯à ¢«¥­¨ï ( > 0 { ª®íää¨æ¨¥­â ãᨫ¥­¨ï ¤ ¯â 樨):

ᮮ⢥âá⢨¨ á ⥮६®© 1 ç¨á«® ª®íää¨æ¨¥­â®¢ ¬®¤¥«¨ "¢å®¤-¢ë室" ¤®«¦­® ¡ëâì ­ ¥¤¨­¨æã ¬¥­ìè¥ à §¬¥à­®á⨠¨á室­®© ­¥¯à¥à뢭®© á¨á⥬ë. ¤­ ª® ¨­â¥à¥á­® ¨áá«¥¤®- ¢ âì ¢®¯à®á ®¡ 㢥«¨ç¥­¨¨ ¨«¨ 㬥­ì襭¨¨ ç¨á« ª®íää¨æ¨- ¥­â®¢ ¬®¤¥«¨ á â®çª¨ §à¥­¨ï ª ª á®åà ­¥­¨ï à ¡®â®á¯®á®¡- ­®á⨠«£®à¨â¬ , â ª ¨ ᪮à®á⨠á室¨¬®á⨠«£®à¨â¬ ¯à¨ ¤®á⨦¥­¨¨ 楫¨ ã¯à ¢«¥­¨ï. ®í⮬㠤«ï ¬®¤¥«¨ ¥áá«¥à ¡ë«¨ ¯à®áç¨â ­ë ¬®¤¥«¨ "¢å®¤-¢ë室" ¤«ï âà¥å, ¤¢ãå ¨ ®¤-

­®£® ª®íää¨æ¨¥­â®¢ ¯à¨ ¯à®ç¨å à ¢­ëå ãá«®¢¨ïå. ®¤¥«¨- ஢ ­¨¥ ¯®ª § «®, ç⮠楫ì ã¯à ¢«¥­¨ï ¤®á⨣ ¥âáï ¤ ¦¥ ¯à¨ ¯à®á⥩襩 ¬®¤¥«¨ á ®¤­¨¬ ª®íää¨æ¨¥­â®¬ (¢¨¤¨¬®, íâ® ®á®- ¡¥­­®áâì ª®­ªà¥â­®© á¨á⥬ë), ­® ¢ áà ¢­¥­¨¨ á ¬®¤¥«ìî á âà¥¬ï ª®íää¨æ¨¥­â ¬¨ ᪮à®áâì á室¨¬®á⨠áãé¥á⢥­­® ¯ - ¤ ¥â.

¥®à¥â¨ç¥áª¨¥ १ã«ìâ âë ¯®¤¢¥à£«¨áì ¯à®¢¥àª¥ ¯®á।- á⢮¬ ª®¬¯ìîâ¥à­®£® ¬®¤¥«¨à®¢ ­¨ï á ¨á¯®«ì§®¢ ­¨¥¬ ¯ - ª¥â [72], ä㭪樮­¨àã饣® ¢ á।¥ MATLAB. à¨á. 13.8, à¨á. 13.9 ¯®ª § ­ë § ¢¨á¨¬®á⨠ª®®à¤¨­ âë Y (t) ¨ ã¯à ¢«ïî饣® ¢®§¤¥©á⢨ï u(t) ª ª ä㭪樨 t ¤«ï 楫¨ ã¯à - ¢«¥­¨ï (13.40) ¯à¨ y = 6 (max Y (t)=4.54 ¤«ï ­¥ã¯à ¢«ï¥¬®© å ®â¨ç¥áª®© á¨á⥬ë). ®®â¢¥âáâ¢ãî騩 ä §®¢ë© ¯®àâà¥â

391