
Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления
.pdf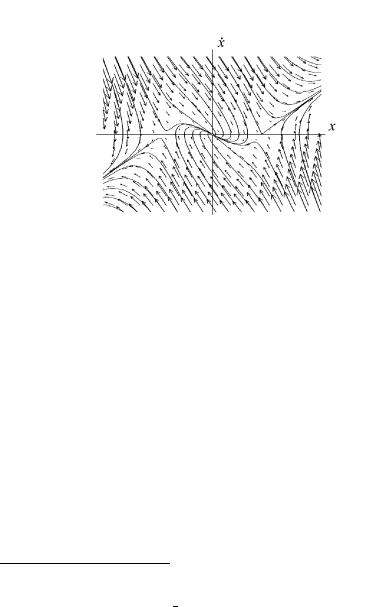
â®à¨©. 2 ª ç¥á⢥ ¯à¨¬¥à à¨á. 5.1 ¯®ª § ë ¯®«¥ ä §®- ¢ëå ᪮à®á⥩ ¨ ä §®¢ë© ¯®àâà¥â á¨áâ¥¬ë ¢â®à®£® ¯®à浪 . ( ®¤¥«¨à®¢ « áì à áᬮâà¥ ï ¢ [94] ¥«¨¥© ï á¨á⥬
x + 2x ; 3x + 4 sat(x) = 0 sat( ) { äãªæ¨ï áë饨ï, á¬. á. 226).
¨á. 5.1. ®«¥ ä §®¢ëå ᪮à®á⥩.
5.2.2. ®áâ®ï¨ï à ¢®¢¥á¨ï á¨á⥬ë
¯à®áâà á⢥ á®áâ®ï¨© á¨áâ¥¬ë ¬®£ãâ ¡ëâì ®á®¡ë¥ â®ç- ª¨, ¢ ª®â®àëå ¢¥ªâ®à ä §®¢®© ᪮à®á⨠®¡à é ¥âáï ¢ ®«ì, v(x) = 0: â® ãá«®¢¨¥ íª¢¨¢ «¥â® ⮬ã, çâ® ¤ ë¥ â®çª¨ ¯à¥¤áâ ¢«ïîâ ᮡ®© á®áâ®ï¨ï (¯®«®¦¥¨ï) à ¢®¢¥á¨ï á¨-
á⥬ë [12, 79]. ª¨¬ ®¡à §®¬, ¥á«¨ ¤«ï ¥ª®â®à®© x0 ¢ë¯®«- ¥® v(x0) = 0 â® ¨¬¥¥âáï à¥è¥¨¥ x(t) x0: ¯à ¢¥¤«¨¢® ¨ ®¡à ⮥ ã⢥ত¥¨¥ { ª ¦¤®¬ã à¥è¥¨î x(t) x0 ᮮ⢥â- áâ¢ã¥â ã«¥¢®© ¢¥ªâ®à ä §®¢®© ᪮à®á⨠¢ â®çª¥ x0: ª ®â- ¬¥ç¥® ¢ëè¥, ä §®¢ë¥ âà ¥ªâ®à¨¨ ¢ á®áâ®ï¨ïå à ¢®¢¥á¨ï ¢ë஦¤ îâáï ¢ â®çª¨, ¢¥ªâ®àë ä §®¢®© ᪮à®á⨠"¨ªã¤
¥ ¯à ¢«¥ë" (¢ í⮬ á¬ëá«¥ â ª¨¥ â®çª¨ "®á®¡ë¥").
áᬮâਬ á®áâ®ï¨ï à ¢®¢¥á¨ï á¨á⥬ë (5.1). § ¨§«®-
¦¥®£® ïá®, çâ® ¬®¦¥á⢮ X0 = fx0g á®áâ®ï¨© à ¢®¢¥á¨ï
2 í⮬ ᢮©á⢥ ®á®¢ â ª §ë¢ ¥¬ë© ¬¥â®¤ ¨§®ª«¨, ïî- 騩áï ¯à¨¡«¨¦¥ë¬ £à ä® «¨â¨ç¥áª¨¬ ¬¥â®¤®¬ ¯®áâ஥¨ï ä §®¢ëå ¯®àâà¥â®¢ ¥«¨¥©ëå á¨á⥬ x = f(x) ¢â®à®£® ¯®à浪 . á¢ï§¨ á à §- ¢¨â¨¥¬ ¢ëç¨á«¨â¥«ìëå á।á⢠ª áâ®ï饬㠢६¥¨ ¬¥â®¤ ¨§®ª«¨ ¯®â¥àï« á¢®¥ § 票¥.
112

í⮩ á¨áâ¥¬ë ®¯à¥¤¥«ï¥âáï «¨¥©ë¬ ãà ¢¥¨¥¬ |
|
Ax0 = 0 |
(5.2) |
£¤¥ A { n n-¬ âà¨æ , x0 { n-¬¥àë© ¢¥ªâ®à. ª ¨§¢¥áâ® ¨§ «¨¥©®© «£¥¡àë [53, 66, 115], ãà ¢¥¨¥ (5.2) ¨¬¥¥â ¥¤¨- á⢥®¥ âਢ¨ «ì®¥ à¥è¥¨¥ x0 = 0 ¢ ⮬ ¨ ⮫쪮 ⮬ á«ã-
ç ¥, ª®£¤ ¬ âà¨æ A ¥¢ë஦¤¥ ï: detA =6 0: áᬮâਬ, çâ® íâ® ®§ ç ¥â á â®çª¨ §à¥¨ï ᢮©á⢠¤¨ ¬¨ç¥áª®© á¨áâ¥- ¬ë. ®áª®«ìªã å à ªâ¥à¨áâ¨ç¥áª¨© ¬®£®ç«¥ A(s), â.¥. § - ¬¥ â¥«ì ¯¥à¥¤ â®ç®© äãªæ¨¨ á¨áâ¥¬ë ¢ëà ¦ ¥âáï à ¢¥- á⢮¬ A(s) = det(sIn ;A) 室¨¬, çâ® A(0) an = (;1)ndetA: ç¨â, ᢮¡®¤ë© ç«¥ å à ªâ¥à¨áâ¨ç¥áª®£® ¬®£®ç«¥ á
â®ç®áâìî ¤® § ª ᮢ¯ ¤ ¥â á ®¯à¥¤¥«¨â¥«¥¬ ¬ âà¨æë A:᫨ ® ¥ à ¢¥ ã«î, â® ã á¨á⥬ë (5.1) ¡ã¤¥â ¥¤¨á⢥- ®¥ ã«¥¢®¥ á®áâ®ï¨¥ à ¢®¢¥á¨ï. á«®¢¨¥ an = 0 ¢ë¯®«- ï¥âáï ¤«ï §¢¥ì¥¢ ¨â¥£à¨àãî饣® ⨯ . ¬¥® ¤«ï ¨å ¢®§¬®¦ë ¥ã«¥¢ë¥ á®áâ®ï¨ï à ¢®¢¥á¨ï. áᬮâਬ íâ® ¯®¤à®¡¥¥.
ª ª ª ¤«ï ¢á¥å x0 |
2 X |
0 |
¨¬¥¥â ¬¥áâ® à ¢¥á⢮ Ax0 = 0 |
||||||||
â® X |
0 |
|
|
|
|
3 |
¬ âà¨æë A , X |
0 |
= N (A): |
||
|
ï¥âáï ã«ì-¯à®áâà á⢮¬ |
|
|
||||||||
ª ¨§¢¥áâ®, [53, 115], ¯à®áâà á⢮ |
N(A) ï¥âáï «¨¥©- |
||||||||||
ë¬ ¯®¤¯à®áâà á⢮¬ |
¯à®áâà á⢠|
|
X: §¬¥à®áâì ¯à®- |
||||||||
áâà á⢠|
N (A) à ¢ |
à §®á⨠¬¥¦¤ã à §¬¥à®áâìî ¯à®- |
|||||||||
áâà á⢠|
X ¨ à £®¬ ¬ âà¨æë A : dimN(A) = n ; rankA: - |
||||||||||
ª¨¬ ®¡à §®¬, ¢ § ¢¨á¨¬®á⨠®â ¬ âà¨æë A (в®з¥¥, ®в ¥¥ а - £ ) б®бв®п¨п а ¢®¢¥б¨п «¨¥©®© б¨бв¥¬л п¢«повбп «¨¡® в®зª®© f0g, «¨¡® ¯àאַ©, ᮤ¥à¦ 饩 íâã â®çªã, «¨¡® ¯«®á- ª®áâìî, ¯à®å®¤ï饩 ç¥à¥§ ç «® ª®®à¤¨ â, «¨¡® «¨¥©ë¬ ¯®¤¯à®áâà á⢮¬ ¡®«¥¥ ¢ë᮪®© à §¬¥à®áâ¨.
5.2.3. ¥ª®¬¯®§¨æ¨ï ¯à®áâà á⢠á®áâ®ï¨©
ëè¥, ¢ ¯. 3.1.2. ¨á¯®«ì§®¢ «®áì ¯®ï⨥ ¨¢ ਠâëå ¯®¤- ¯à®áâà áâ¢. áᬮâਬ ¥£® ¡®«¥¥ ¯®¤à®¡®.
¯®¬¨¬ á«¥¤ãî騥 ¯®«®¦¥¨ï [53, 115].¯à¥¤¥«¥¨¥. à®áâà á⢮ X ï¥âáï ¯àאַ© á㬬®©
᢮¨å ¯®¤¯à®áâà á⢠X1 X2 : : : Xm (¨®£¤ § ¯¨áë¢ îâ
X = X1 X2 Xm), ¥á«¨ :
3 ã«ì-¯à®áâà á⢮¬ ( 㫨àã¥¬ë¬ ¯à®áâà á⢮¬) N(A) ¬ âà¨- æë A §ë¢ ¥âáï ¬®¦¥á⢮ fxg â ª®¥, çâ® ¤«ï ¢á¥å x 2 N(A) ¢ë¯®«¥® Ax = 0 [53, 115]. 祢¨¤®, çâ® ¢á¥£¤ â®çª f0g 2 N(A).
113
¤«ï ¢á类£® x 2 X |
áãé¥áâ¢ã¥â à §«®¦¥¨¥ x = x1 + x2 + |
||||
+ xm £¤¥ x1 2 X1 : : : xm 2 Xm: |
|
|
|||
íâ® à §«®¦¥¨¥ ¥¤¨á⢥®. (¤ ®¥ ãá«®¢¨¥ ¬®¦® |
|||||
§ ¯¨á âì ¢ íª¢¨¢ «¥â®© ¡®«¥¥ ¯à®á⮩ ä®à¬¥, |
¨¬¥®: |
||||
¥á«¨ x = x1 + x2 + + xm = 0 £¤¥ x1 2 X1 |
: : : |
x1 2 Xm â® |
|||
x1 = x2 = |
= xm = 0): |
2 |
|
|
|
|
|
|
|||
§ ¥¤¨á⢥®áâ¨ à §«®¦¥¨ï á«¥¤ã¥â, çâ® ¢á直¥ ¯®¤- |
|||||
¯à®áâà á⢠|
X1 : : : Xm ¨¬¥îâ ®¡é¨¬ «¨èì ®¤¨ í«¥¬¥â |
||||
f0g: |
|
A ¨¬¥¥â ¢ ¯à®áâà á⢥ X |
¨¢ ਠâë¥ |
||
᫨ ¬ âà¨æ |
|||||
¯®¤¯à®áâà á⢠|
X1 : : : |
Xm â.¥. ¤«ï ¢á¥å x |
2 Xi ¢ë¯®«¥® |
||
Ax 2 Xi i = 1 2 : : : m, ¨ ¥á«¨ ¯à®áâà á⢮ X ¬®¦® ¯à¥¤áâ - |
|||||
¢¨âì ¢ ¢¨¤¥ ¯àאַ© áã¬¬ë ¨¢ ਠâëå ¯®¤¯à®áâà áâ¢, â®
¥¢ë஦¤¥ë¬ ¯à¥®¡à §®¢ ¨¥¬ ¬ âà¨æ ¬®¦¥â ¡ëâì ¯à¨- ¢¥¤¥ ª ¡«®ç®-¤¨ £® «ì®¬ã ¢¨¤ã. ¯à ¢¥¤«¨¢® ¨ ®¡à â-
®¥ ã⢥ত¥¨¥: ¥á«¨ ¬ âà¨æ ¨¬¥¥â ª¢ §¨¤¨ £® «ìãî (¡«®ç®-¤¨ £® «ìãî) áâàãªâãàã, â® ¯à®áâà á⢮ X à §- « £ ¥âáï ¯àï¬ãî á㬬㠨¢ ਠâëå (¯® ®â®è¥¨î ª ¤ ®© ¬ âà¨æ¥) ¯®¤¯à®áâà áâ¢.
᫨ 㫨àãî騩 ¬®£®ç«¥ f (s) (á¬. 3.2.) ¬ âà¨æë A à §«®¦¨âì ¢ ¯à®¨§¢¥¤¥¨¥ ¤¢ãå ¢§ ¨¬®-¯à®áâëå ¬®¦¨â¥-
«¥©: f (s) = f1(s)f2 |
(s) â® ¯à®áâà á⢮ X |
¬®¦® à §«®¦¨âì ¢ |
||||
¯àï¬ãî á㬬㠤¢ãå ¯®¤¯à®áâà á⢠X = |
X1 X2 ¨¢ ਠâ- |
|||||
ëå ®â®á¨â¥«ì® ¬ âà¨æë A: |
|
|
||||
᫨ ¥ª®â®àë© |
㫨àãî騩 ¬®£®ç«¥ f(s) ¬ âà¨æë A |
|||||
|
|
|
Q |
|
|
|
|
|
|
m |
|
|
|
¯à¥¤áâ ¢¨âì ¢ ¢¨¤¥ f (s) = i=1 |
(s ; si)ri £¤¥ si { ¢á¥ (à §«¨çë¥) |
|||||
ª®à¨ ¬®£®ç«¥ , ri { ¨å ªà â®áâ¨, â® ¯à®áâà á⢮ |
||||||
à §« £ ¥âáï ¯àï¬ãî á㬬ã m ¯®¤¯à®áâà á⢠X1 : : : XmX |
||||||
¨¢ ਠâëå ®â®á¨â¥«ì® ¬ âà¨æë A ¯à¨ç¥¬ í⨠¯®¤¯à®- |
||||||
бва бв¢ п¢«повбп г«м-¯а®бва бв¢ ¬¨ ¬ ва¨жл (siI;A)ri : |
||||||
ª®¥æ, ¥á«¨ |
|
㫨àãî騩 ¬®£®ç«¥ f (s) ¬ âà¨æë A |
||||
¯à¥¤áâ ¢¨âì ¢ ¢¨¤¥ |
|
|
|
|
||
|
m |
|
q |
|
|
|
f (s) = |
Y |
(s ; si)ri |
Y |
(s2 ; 2 j + j2 + j2)pj |
||
|
i=1 |
|
j=1 |
|
|
|
£¤¥ si { ¢á¥ à §«¨çë¥ ¢¥é¥áâ¢¥ë¥ ª®à¨ ¬®£®ç«¥ , sj j+1 = j | j { à §«¨çë¥ ¥¢¥é¥áâ¢¥ë¥ ª®à¨, â® ¯à®- áâà á⢮ X à §« £ ¥âáï ¯àï¬ãî á㬬㠨¢ ਠâëå
114

|
m |
|
|
q |
|
|
X = |
X |
r |
|
X |
c |
|
k=1 |
Xk |
k=1 |
Xj |
: |
||
ª®¬ã à §¡¨¥¨î ¯à®áâà á⢠|
á®áâ®ï¨© á¨á⥬ë ᮮ⢥â- |
|||||
áâ¢ã¥â ¯à¨¢¥¤¥¨¥ ¬ âà¨æë A ª ª ®¨ç¥áª®© ä®à¬¥ ®à¤ - (2.1.3.).
áå®¤ï ¨§ ¨§«®¦¥®£®, ¯à®áâà á⢮ á®áâ®ï¨© X á¨áâ¥- ¬ë ¬®¦® ¯à¥¤áâ ¢¨âì ¢ ¢¨¤¥ ¯àאַ© á㬬ë L ¨¢ ਠâëå
¯®¤¯à®áâà á⢠XiA, â.¥. ª ¦¤ë© ¢¥ªâ®à x 2 X § ¯¨á âì ¢ ¢¨¤¥ «¨¥©®© ª®¬¡¨ 樨 x = PLi=1 ixi £¤¥ xi 2 XiA i = 1 2 : : : L ([3, 53]). áᬮâਬ á¢ï§ì í⮣® à §¡¨¥¨ï á ä §®¢ë¬¨ ¯®à- âà¥â ¬¨ á¨á⥬ë, ®¡à é ï ®á®¢®¥ ¢¨¬ ¨¥ á«ãç © ¯à®- áâëå ᮡá⢥ëå ç¨á¥«.
᫨ ¬ âà¨æ A ¨¬¥¥â ¯®¯ à® à §«¨çë¥ ª®à¨ å à ªâ¥-
à¨áâ¨ç¥áª®£® ¬®£®ç«¥ , â® ¥âਢ¨ «ì묨 ¢¥é¥á⢥ë- ¬¨ ¨¢ ਠâ묨 ¯®¤¯à®áâà á⢠¬¨ ¨¬¥ì襩 à §¬¥à- ®á⨠¡ã¤ãâ ᮡáâ¢¥ë¥ ¯àï¬ë¥ (¤«ï ¢¥é¥á⢥ëå ª®à¥©) ¨ ᮡáâ¢¥ë¥ ¯«®áª®á⨠(¤«ï ¬¨¬ëå ª®¬¯«¥ªá®-ᮯà殮- ëå ª®à¥© å à ªâ¥à¨áâ¨ç¥áª®£® ¬®£®ç«¥ ). ãáâì - ç «ì®¥ á®áâ®ï¨¥ á¨áâ¥¬ë ¯à¨ ¤«¥¦¨â ᮡá⢥®© ¯àï-
¬®© i |
ᮮ⢥âáâ¢ãî饩 (¯à®á⮬ã) ¢¥é¥á⢥®¬ã ª®àî |
||||||
si â.¥. |
x0 |
= |
i xi |
£¤¥ |
i |
2 R { ¥ª®â®à®¥ ç¨á«®, |
xi { |
G |
|
|
0 0 |
|
0 |
|
0 |
ᮡáâ¢¥ë© ¢¥ªâ®à, ®â¢¥ç î騩 ᮡá⢥®¬ã § 票î si:
«ï ¢¥ªâ®à |
ä §®¢®© ᪮à®á⨠¢ í⮩ â®çª¥ ¬®¦® § ¯¨á âì |
||
v(x ) = Ax |
0 |
= 0s x0 |
: ®í⮬㠢¥ªâ®à ä §®¢®© ᪮à®á⨠¡ã¤¥â |
0 |
i i i |
|
|
¯à ¢«¥ ¯® í⮩ ¦¥ ¯àאַ©. 4 ¨ ᮡáâ¢¥ë¥ ¯àï¬ë¥ á¨-
á⥬ë ᮮ⢥âáâ¢ãîâ ¥ª®â®àë¬ ä §®¢ë¬ âà ¥ªâ®à¨ï¬. «¥- ¤®¢ ⥫ì®, ¢áï ä §®¢ ï âà ¥ªâ®à¨ï ®áâ ¥âáï ¯àאַ© Gi 5 ਠ㪠§ ëå ç «ìëå ãá«®¢¨ïå ¥âà㤮 ¯®«ãç¨âì ¨ ä®à¬ã«ã ¤«ï ¯à®æ¥áá x(t): ¥©á⢨⥫ì®, â ª ª ª ¢ë¯®«¥- ® (5.1), â® x(t) = six(t) x(0) = 0i x0i : âáî¤ ¯®«ãç ¥¬ à¥è¥- ¨¥ x(t) = esitx(0): â® ¢ëà ¦¥¨¥ ¬®¦® § ¯¨á âì ¨ ¢ á«¥¤ãî-
饬 ¢¨¤¥. ¢¥¤¥¬ äãªæ¨î i(t) 2 R ª ª à¥è¥¨¥ ãà ¢¥¨ï
4 âண®¥ ¤®ª § ⥫ìá⢮ í⮣® ä ªâ ¯à¨¢¥¤¥®, ¯à¨¬¥à, ¢ [12].
5 ¬¥â¨¬, çâ® ä §®¢ ï âà ¥ªâ®à¨ï ¯à¨ ¤«¥¦¨â ᮡá⢥®© ¯àאַ©, ® ¥«ì§ï áç¨â âì, çâ® ¯àï¬ ï Gi ï¥âáï ä §®¢®© âà ¥ªâ®à¨¥©. ¥©- á⢨⥫ì®, ¯àאַ© Gi «¥¦ â ¯® ªà ©¥© ¬¥à¥ âਠ¥¯¥à¥á¥ª î騥áï ä §®¢ë¥ âà ¥ªâ®à¨¨: ¤¢¥ ¨§ ¨å 室ïâáï ¯® à §ë¥ áâ®à®ë ®â ç « ª®®à¤¨ â, âà¥âìï ¥áâì â®çª f0g: ஬¥ ⮣®, ¯à¨ si = 0 ª ¦¤ ï â®çª ¯àאַ© Gi ï¥âáï ®â¤¥«ì®© ä §®¢®© âà ¥ªâ®à¨¥©.
115

|
(t) |
= s |
(t) |
(0) |
= 0: ®£¤ x(t) = |
|
(t)x0: 祢¨¤®, |
i |
|
i i |
|
i |
i |
i |
i |
çâ® i(t) = esit i0: ª¨¬ ®¡à §®¬, ¨§®¡à ¦ îé ï â®çª ¡ã¤¥â |
|||||||
¤¢¨£ âìáï ¢¤®«ì ¯àאַ© Gi á ª®íää¨æ¨¥â®¬ i(t): ¯à ¢«¥- |
|||||||
¨¥ ¤¢¨¦¥¨ï ®¯à¥¤¥«ï¥âáï § ª®¬ si : ¯à¨ si < 0 ¤¢¨¦¥¨¥ |
|||||||
¡ã¤¥â ¯à ¢«¥® ª á®áâ®ï¨î à ¢®¢¥á¨ï |
f0g, ¯à¨ si > 0 { |
||||||
®â â®çª¨ f0g, |
¯à¨ si |
= 0 { x(t) 6x0, ¨ ª ¦¤ ï â®çª ¯àאַ© |
|||||
ï¥âáï á®áâ®ï¨¥¬ à ¢®¢¥á¨ï. |
|
|
|||||
¡®¡é ï ¯à¨¢¥¤¥ë¥ à áá㦤¥¨ï, ¯à¨¬¥¬, çâ® á¨á⥬ ®¡« ¤ ¥â k ¯à®áâ묨 ¢¥é¥á⢥묨 ª®àﬨ. ª ®â¬¥ç¥®
¢ëè¥, ¨¬ ®â¢¥ç ¥â k «¨¥©® ¥§ ¢¨á¨¬ëå ᮡá⢥ëå ¢¥ª- â®à®¢ ¨, ᮮ⢥âá⢥®, k ᮡá⢥ëå ¯àï¬ëå [3, 53, 115]. § «¨¥©®á⨠á¨á⥬ë á«¥¤ã¥â, çâ® ¤¢¨¦¥¨¥ ¯à¨ ¯à®¨§¢®«ì- ëå ç «ìëå ãá«®¢¨ïå ¬®¦® ¯à¥¤áâ ¢¨âì, ª ª á㯥௮§¨- æ¨î ¤¢¨¦¥¨© ¯® ᮡáâ¢¥ë¬ ¯à ¢«¥¨ï¬. ®«¥¥ ¯®¤à®¡- ®: ¥á«¨ ç «ì®¥ á®áâ®ï¨¥ x(0) ¯à¨ ¤«¥¦¨â ¨¢ ਠâ- ®¬ã ¯®¤¯à®áâà áâ¢ã, ¯®à®¦¤¥®¬ã ᮡá⢥묨 ¢¥ªâ®-
à ¬¨ x01 x02 : : : x0k â® íâ® á®áâ®ï¨¥ ¬®¦® à §«®¦¨âì ¯® ¡ -
§¨áã, á®áâ®ï饬㠨§ ᮡá⢥ëå ¢¥ªâ®à®¢: x(0) = Pki=1 ix0i :
®£¤ à¥è¥¨¥ x(t) ¨¬¥¥â ¢¨¤: x(t) = Pki=1 i (t)x0i £¤¥ i(t) =
esit 0i :
᫨ ¨¬¥îâáï ¯à®áâë¥ ¬¨¬ë¥ ª®¬¯«¥ªá®-ᮯà殮ë¥
ª®à¨ å à ªâ¥à¨áâ¨ç¥áª®£® ¬®£®ç«¥ , â® ®¨ ¥ ®¯à¥¤¥«ï- îâ ¨ª ª®£® ᮡá⢥®£® ¯à ¢«¥¨ï ¢ ¢¥é¥á⢥®¬ ¯à®- áâà á⢥. ¤ ª® á ¯®¬®éìî ¨§«®¦¥®£® ¢ ¯. 3.1.2. ¯à¨¥¬ â ª¨¬ ª®àï¬ ¬®¦® ¯®áâ ¢¨âì ¢ ᮮ⢥âá⢨¥ ᮡá⢥ãî ¯«®áª®áâì, ª®â®à ï â ª¦¥ ï¥âáï ¨¢ ਠâë¬ ¯®¤¯à®- áâà á⢮¬ ¬ âà¨æë A: áá㦤 ï «®£¨ç® ¯à¥¤ë¤ã饬ã á«ãç î ¯à¨å®¤¨¬ ª ¢ë¢®¤ã, çâ® âà ¥ªâ®à¨ï, ç¨ îé ïáï ᮡá⢥®© ¯«®áª®á⨠¡ã¤¥â ¥© ¢á¥£¤ ¯à¨ ¤«¥¦ âì.
ª®з в¥«м® ¬®¦® б¤¥« вм ¢л¢®¤, зв® ¯а¨ ®вбгвбв¢¨¨ ªа вле ª®а¥© е а ªв¥а¨бв¨з¥бª®£® ¬®£®з«¥ д §®¢го ва ¥ªв®а¨о ¬®¦® ¯®«гз¨вм бг¯¥а¯®§¨ж¨¥© ¤¢¨¦¥¨© ¯® б®¡-
áâ¢¥ë¬ ¯àï¬ë¬ ¨ ᮡáâ¢¥ë¬ ¯«®áª®áâï¬.
«ãç © ªà âëå ª®à¥© ¡®«¥¥ á«®¦¥, â ª ª ª ¯à¨ ¥¬ ¢®§- ¬®¦ë á¨âã 樨, ¢ ª®â®àëå ¥«ì§ï à §«®¦¨âì ¯à®áâà á⢮ á㬬㠨¢ ਠâëå ¯®¤¯à®áâà áâ¢ à §¬¥à®á⨠¥ ¡®- «¥¥ ¤¢ãå.
á«¥¤ãî饬 ¯ à £à ä¥ ¢¨¤ ä §®¢ëå âà ¥ªâ®à¨© ¯«®á-
6 ¯®¬¨¬, çâ® §¤¥áì ¬ë à áᬠâਢ ¥¬ á«ãç © ¯à®áâëå ¢¥é¥á⢥- ëå ª®à¥©.
116

ª®á⨠¡ã¤¥â à áᬮâॠ¡®«¥¥ ¯®¤à®¡®.
5.3.¨¤ë ä §®¢ëå ¯®àâà¥â®¢ ¤«ï á¨á⥬ ¢â®à®£® ¯®- à浪
áᬮâਬ «¨¥©ë¥ á¨áâ¥¬ë ¢â®à®£® ¯®à浪 , X = R2: å á®áâ®ï¨¥ ¬®¦® ¨§®¡à §¨âì ¢ ¢¨¤¥ â®çª¨ ¯«®áª®á⨠7.
áᬮâਬ ¥ª®â®àë¥ á«ãç ¨.
ãáâì ᮡáâ¢¥ë¥ ç¨á« s1 s2 ¬ âà¨æë A ¤¥©á⢨⥫ì- ë ¨ ®â«¨çë ®â ã«ï, s1 =6 s2: ®£¤ ¨¬¥îâáï ¥¤¨á⢥®¥ á®áâ®ï¨¥ à ¢®¢¥á¨ï ¢ â®çª¥ f0g ¨ ¤¢¥ ¥á®¢¯ ¤ î騥 ᮡ- áâ¢¥ë¥ ¯àï¬ë¥ G1 G2: ᫨ si < 0 â® ¤¢¨¦¥¨¥ ¨§®¡à ¦ î- 饩 â®çª¨ ¯® ¯àאַ© Gi ¯à ¢«¥® ª á®áâ®ï¨î à ¢®¢¥á¨ï,
¥á«¨ si > 0 { ®â í⮣® á®áâ®ï¨ï. ਠsi = 0 ¨§®¡à ¦ îé ï â®çª ¯àאַ© Gi ¥¯®¤¢¨¦ . ⬥⨬ â ª¦¥, çâ® â®çª , à ᯮ«®¦¥ ï ¬¥¦¤ã ¥ª®â®à묨 «ãç ¬¨ ᮡá⢥ëå ¯àï- ¬ëå, ¢ ¯à®æ¥áᥠ¤¢¨¦¥¨ï ¢á¥£¤ ®áâ ¥âáï ¬¥¦¤ã ¨¬¨, â ª ª ª ¯® í⨬ «ãç ¬ ¯à®å®¤ïâ ä §®¢ë¥ âà ¥ªâ®à¨¨, à §«¨ç-
ë¥ ä §®¢ë¥ âà ¥ªâ®à¨¨ ¯¥à¥á¥ª âìáï ¥ ¬®£ãâ.
®«¥¥ ¤¥â «ì®¥ ®¯¨á ¨¥ ä §®¢®£® ¯®àâà¥â á¨áâ¥¬ë § - ¢¨á¨â ®â § ª®¢ s1,s2:
1. áâ®©ç¨¢ë© ã§¥«. ᫨ s1 < 0 s2 < 0 ¢á¥ ä §®¢ë¥ âà ¥ªâ®à¨¨ ¯à ¢«¥ë ª á®áâ®ï¨î à ¢®¢¥á¨ï { â®çª¥ f0g { ¨ ᨬ¯â®â¨ç¥áª¨ ª ¥¬ã ¯à¨¡«¨¦ îâáï (á¬. à¨á. 5.2, ).
¨á⥬ ᨬ¯â®â¨ç¥áª¨ ãá⮩稢 . ª®© ä §®¢ë© ¯®àâà¥â ᢮©á⢥¥ ᮡáâ¢¥ë¬ ¤¢¨¦¥¨ï¬ ¯¥à¨®¤¨ç¥áª®£® §¢¥ ¢â®à®£® ¯®à浪 , ¨¬¥î饣® ¯¥à¥¤ â®çãî äãªæ¨î
W(s) = |
K |
|
(T1 > 0 T2 > 0): |
(T1 s + 1)(T2s + 1) |
2. ¥ãáâ®©ç¨¢ë© ã§¥«. ᫨ s1 > 0 s2 > 0 â® ª à- â¨ ä §®¢ëå âà ¥ªâ®à¨© ⮦¥ ¨¬¥¥â ¢¨¤ 㧫 , ® ¯à - ¢«¥¨¥ ¤¢¨¦¥¨ï ¬¥ï¥âáï ¯à®â¨¢®¯®«®¦®¥. ª®© ⨯
7 ¥б¬®вап в®, зв® ®¡лз® ¨бб«¥¤говбп б¨бв¥¬л ¡®«¥¥ ¢лб®ª®£® ¯®- ап¤ª , ¨§гз¥¨¥ ¤¢¨¦¥¨© ¯«®бª®бв¨ ®ª §л¢ ¥вбп ¯®«¥§л¬. ¥©бв¢¨- в¥«м®, ¯а¨ ¯а®бвле б®¡бв¢¥ле з¨б« е ¬ ва¨жл A á¨á⥬ "à ᯠ¤ - ¥âáï" àï¤ ¯®¤á¨á⥬ ¥ ¢ëè¥ ¢â®à®£® ¯®à浪 . ஬¥ ⮣®, ç áâ® ¯à¨ ¨áá«¥¤®¢ ¨¨ ¬®¦® ¯à¥¥¡à¥çì ¬ «ë¬¨ ¯®áâ®ï묨 ¢à¥¬¥¨. ®£¤ ¯®¢¥¤¥¨¥ á¨á⥬ë á ¤®áâ â®ç®© ¤«ï ¯à ªâ¨ª¨ â®ç®áâìî ®¯¨áë¢ ¥âáï ãà ¢¥¨ï¬¨ ¢â®à®£® ¯®à浪 .
117
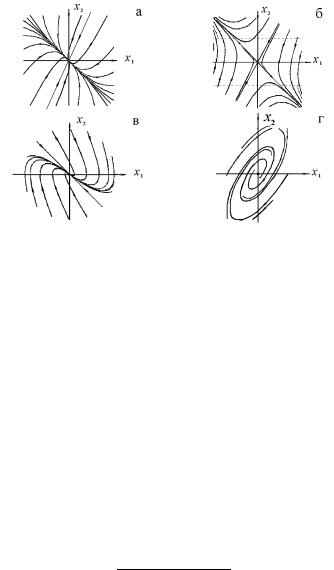
¨á. 5.2. §®¢ë¥ ¯®àâà¥âë á¨á⥬ ¢â®à®£® ¯®à浪 .
¯®¢¥¤¥¨ï ᢮©á⢥¥ ¥ãáâ®©ç¨¢ë¬ á¨á⥬ ¬. ਬ¥à { ᮡáâ¢¥ë¥ ¤¢¨¦¥¨ï §¢¥ á ¯¥à¥¤ â®ç®© äãªæ¨¥©
W(s) = |
K |
(T1 > 0 T2 > 0): |
|
|
|
||
(T1 s ; 1)(T2s ; 1) |
|||
3. ¥¤«®. |
᫨ § ª¨ ᮡá⢥ëå ç¨á¥« ¯à®â¨¢®¯®- |
||
«®¦ë ¬¥¦¤ã ᮡ®©, ¯à¨¬¥à, s1 |
> 0 s2 < 0 â® ¯® ¯àאַ© |
||
G1 ¤¢¨¦¥¨¥ ¯à®¨á室¨â ®â á®áâ®ï¨ï à ¢®¢¥á¨ï, ¯® ¯àï- |
|||
¬®© G2 { ª í⮬ã á®áâ®ï¨î (á¬. à¨á. 5.2, ¡). ¥á¬®âàï |
|||
â®, çâ® §¤¥áì ¨¬¥îâáï âà ¥ªâ®à¨¨, ¯à ¢«¥ë¥ ª ç «ã |
|||
ª®®à¤¨ â ¨ ᮮ⢥âáâ¢ãî騥 § âãå î騬 ¯à®æ¥áá ¬, ᥤ- «® ᢮©á⢥® ¥ãáâ®©ç¨¢ë¬ á¨á⥬ ¬. ਬ¥à { §¢¥® á ¯¥à¥¤ â®ç®© äãªæ¨¥©
W(s) = |
K |
|
(T1 > 0 T2 > 0): |
(T1 s ; 1)(T2s + 1) |
4. ¤¨ ¨§ ª®à¥© ¨¬¥¥â ã«¥¢®¥ § 票¥. ãáâì, -
¯à¨¬¥à, s1 = 0 s2 6= 0: ®£¤ ¯àï¬ ï G1 ®¡à §ã¥â ¬®¦¥á⢮ á®áâ®ï¨© à ¢®¢¥á¨ï á¨áâ¥¬ë ¨ ¤¢¨¦¥¨ï ¯® ¥© ¥ ¯à®¨áå®- ¤¨â. §®¢ë© ¯®àâà¥â á®á⮨⠨§ ¯àï¬ëå, ¯ à ««¥«ìëå G1:᫨ s2 < 0 â® ¤¢¨¦¥¨¥ ¯® âà ¥ªâ®à¨ï¬ ¯à ¢«¥® ¢ áâ®- à®ã ¯àאַ© G1 ¨ ç¥ { ¢ ¯à®â¨¢®¯®«®¦ãî áâ®à®ã. ª¨¥
118
¯à®æ¥ááë ᢮©á⢥ë ãá⮩稢®¬ã ¨ ¥ãá⮩稢®¬ã ¨â¥- £à¨àãî騬 §¢¥ìï¬ á ¯¥à¥¤ â®ç묨 äãªæ¨ï¬¨
W(s) = |
K |
¨ W(s) = |
K |
|
|
|
|
||
s(T2s + 1) |
s(T2s ; 1) |
|||
ᮮ⢥âá⢥® (T1 > 0 T2 > 0).
5. ¡ ª®àï à ¢ë ã«î. ë© á«ãç © ®â¢¥ç ¥â - «¨ç¨î ã á¨áâ¥¬ë ªà âëå ᮡá⢥ëå ç¨á¥«, ¨ ¢¨¤ ä §®¢®- £® ¯®àâà¥â § ¢¨á¨â ®â à §¬¥à ¦®à¤ ®¢ëå ª«¥â®ª. ᫨ ¦®à¤ ®¢ ä®à¬ ¬ âà¨æë A ¯à¥¤áâ ¢«¥ ¤¢ã¬ï ª«¥âª ¬¨ ¯¥à¢®£® ¯®à浪 (â.¥. ¬ âà¨æ ®à¤ ã«¥¢ ï), â® ä §®-
¢л¥ ва ¥ªв®а¨¨ ¯а¥¤бв ¢«пов б®¡®© в®зª¨ ¯«®бª®бв¨ ¨ ª ¦¤®¥ б®бв®п¨¥ б¨бв¥¬л ¥бвм б®бв®п¨¥ а ¢®¢¥б¨п. а¨- ¬¥а®¬ в ª®© б¨бв¥¬л п¢«повбп ¤¢ ¥§ ¢¨б¨¬ле ¬¥¦¤г б®- ¡®© ¨¤¥ «мле ¨в¥£а¨агой¨е §¢¥ . б«¨ ¦®а¤ ®¢ ª«¥в- ª ¨¬¥¥в а §¬¥а ¤¢ , в® д §®¢л¥ ва ¥ªв®а¨¨ ¯а¥¤бв ¢«пов б®¡®© ¬®¦¥бв¢® ¯ап¬ле, ¯ а ««¥«мле б®¡бв¢¥®© ¯ап- ¬®©. ® нв®© ¯аאַ© ¤¢¨¦¥¨п ¥ ¯а®¨б室¨в (® ®¡а §г¥в ¬®¦¥бв¢® б®бв®п¨© а ¢®¢¥б¨п), ¯® а §л¥ бв®а®л ®в ¥¥ ¨§®¡а ¦ ой¨¥ в®зª¨ ¤¢¨¦гвбп ¢ ¯а®в¨¢®¯®«®¦ле - ¯а ¢«¥¨пе. ª®© е а ªв¥а д §®¢ле ва ¥ªв®а¨© б¢®©бв¢¥
¤¢®©®¬ã ¨â¥£à¨àãî饬㠧¢¥ã W(s) = Ks2 : ¬¥â¨¬, çâ®
¥á«¨ ¢ ¯¥à¢®¬ á«ãç ¥ á¨á⥬ ¥©âà «ì®-ãá⮩稢 , â® ¢® ¢â®à®¬ { ¥ãá⮩稢 .
6. à âë¥ ¥ã«¥¢ë¥ ¢¥é¥áâ¢¥ë¥ ª®à¨. ᫨ ã á¨- áâ¥¬ë ¨¬¥îâáï ªà âë¥ ¥ã«¥¢ë¥ ¢¥é¥áâ¢¥ë¥ á®¡á⢥- ë¥ ç¨á« s1 = s2, â® â ª¦¥ ¢®§¬®¦ë ¤¢ áãé¥á⢥® à §- «¨çëå á«ãç ï. ᫨ ª ®¨ç¥áª ï ¦®à¤ ®¢ ä®à¬ ¬ - âà¨æë á®á⮨⠨§ ¤¢ãå ª«¥â®ª ¯®à浪 ®¤¨, â® ®¡é¥¥ à¥- 襨¥ ãà ¢¥¨ï (5.1) ¨¬¥¥â ¢¨¤ x(t) = es1t ¨ ®¯¨áë¢ ¥â á®- ¢®ªã¯®áâì «ã祩, ¢ë室ïé¨å ¨§ ç « ª®®à¤¨ â. ਠs1 = s2 < 0 ¤¢¨¦¥¨¥ ¯à®¨á室¨â ¢ ¯à ¢«¥¨¨ ª ç «ã ª®®à¤¨ â, ¯à¨ s1 = s2 > 0 { ¢ ¯à®â¨¢®¯®«®¦ãî áâ®à®-
ã. ਬ¥à®¬ á¨á⥬ë á â ª¨¬ ⨯®¬ ä §®¢ëå âà ¥ªâ®à¨© ï¥âáï á¨á⥬ , á®áâ®ïé ï ¨§ ¤¢ãå ¥§ ¢¨á¨¬ëå ¯¥à¨®¤¨- ç¥áª¨å §¢¥ì¥¢ á à ¢ë¬¨ ¯®áâ®ï묨 ¢à¥¬¥¨.
᫨ ª ®¨ç¥áª ï ¦®à¤ ®¢ ä®à¬ ¬ âà¨æë á®á⮨⠨§ ®¤®© ª«¥âª¨ ¯®à浪 ¤¢ , â® ¨¬¥¥âáï ®¤ ᮡá⢥ ï ¯àï- ¬ ï, ª®â®à®© «¥¦ â ä §®¢ë¥ âà ¥ªâ®à¨¨ ¯à¨ ᮮ⢥âáâ¢ã- îé¨å ç «ìëå ãá«®¢¨ïå ¨ ¬®¦¥á⢮ ªà¨¢ëå, § ¯®«ïî-
119

騥 ¯®«ã¯«®áª®áâ¨, à §¤¥«¥ë¥ ¤ ®© ¯àאַ© (à¨á. 5.2, ¢). ª®© ¢¨¤ ä §®¢®£® ¯®àâà¥â ¢ ®ªà¥áâ®á⨠á®áâ®ï¨ï
à ¢®¢¥á¨ï §ë¢ ¥âáï ãáâ®©ç¨¢ë¬ ¢ë஦¤¥ë¬ 㧫®¬ {
¯à¨ s1 = s2 < 0 ¨ ¥ãáâ®©ç¨¢ë¬ ¢ë஦¤¥ë¬ 㧫®¬ { ¯à¨ s1 = s2 > 0: â®â ä §®¢ëå âà ¥ªâ®à¨© å à ªâ¥à¥ ¤«ï ¯®- á«¥¤®¢ â¥«ì® á®¥¤¨¥ëå ¯¥à¨®¤¨ç¥áª¨å §¢¥ì¥¢ á ®¤¨- ª®¢ë¬¨ ¯®áâ®ï묨 ¢à¥¬¥¨, â.¥. á¨á⥬¥ á ¯¥à¥¤ â®ç®© äãªæ¨¥©
|
K |
|
K |
|
||
W(s) = |
|
¨«¨ W(s) = |
|
|
|
(T > 0): |
(T s + 1)2 |
(T s ; 1)2 |
|||||
áᬮâਬ ⥯¥àì á¨á⥬ã á ¬¨¬ë¬¨ ª®¬¯«¥ªá®-ᮯàï- |
||||||
¦¥ë¬¨ ᮡá⢥묨 ç¨á« ¬¨ s1 2 |
= | |
|
> 0: í⮬ |
|||
á«ãç ¥ â ª¦¥ ¨¬¥¥âáï ¥¤¨á⢥®¥ á®áâ®ï¨¥ à ¢®¢¥á¨ï ¢ |
||||||
â®çª¥ f0g: ¨¤ ä §®¢ëå ¯®àâà¥â®¢ § ¢¨á¨â ®â § 票ï :
7. ®ªãá. ਠ=6 0 ¯®«ãç ¥¬ á¨á⥬㠪ਢëå, ¨¬¥- îé¨å ¢¨¤ 䨮-¨áª ¦¥ëå «®£ à¨ä¬¨ç¥áª¨å á¯¨à «¥©.ਠ< 0 ¤¢¨¦¥¨¥ ¯à®¨á室¨â ª á®áâ®ï¨î à ¢®¢¥á¨ï (ãáâ®©ç¨¢ë© ä®ªãá), ¯à¨ > 0 { ®â í⮣® á®áâ®ï¨ï (¥- ãáâ®©ç¨¢ë© ä®ªãá) (á¬. à¨á. 5.2, ¢).
áâ®©ç¨¢ë© ä®ªãá ᢮©á⢥¥ ª®«¥¡ ⥫ìë¬ §¢¥ìï¬ á ¯¥à¥¤ â®ç®© äãªæ¨¥©
W(s) = |
K |
(0 < < 1 T > 0 ) |
||
|
|
|||
T2s2 + 2 T s + 1 |
||||
¥ãáâ®©ç¨¢ë© { §¢¥ìï¬ |
|
|
|
|
|
W(s) = |
|
K |
|
|
|
|
|
|
|
T2s2 |
; 2 T s + 1 |
||
(á ⥬¨ ¦¥ ¤¨ ¯ §® ¬¨ § 票© ¯ à ¬¥â஢). |
||||
8. ¥âà. ਠ= 0 ¯®«ãç ¥¬ á¨á⥬㠧 ¬ªãâëå í««¨- |
||||
¯â¨ç¥áª¨å âà ¥ªâ®à¨© á æ¥â஬ ¢ ç «¥ ª®®à¤¨ â. ⨬ âà ¥ªâ®à¨ï¬ ᮮ⢥âáâ¢ãîâ ¯¥à¨®¤¨ç¥áª¨¥ ¯à®æ¥ááë á ¯¥à¨- ®¤®¬ 2 = { ¥§ âãå î騥 £ ମ¨ç¥áª¨¥ ª®«¥¡ ¨ï. à¨- ¬¥à®¬ ¬®¦¥â á«ã¦¨âì ª®á¥à¢ ⨢®¥ §¢¥® á ¯¥à¥¤ â®ç®©
äãªæ¨¥© W(s) = K+ 1: T 2s2
¡à ⨬áï ⥯¥àì ª å à ªâ¥àë¬ ®á®¡¥®áâï¬ ä §®¢ëå ¯®àâà¥â®¢ ¯«®áª®á⨠¯à¨ ª ®¨ç¥áª®¬ ¯à¥¤áâ ¢«¥¨¨ ãà ¢¥¨© á®áâ®ï¨ï. áᬮâਬ ¤¨ £® «ìãî (¢¥é¥á⢥- ãî ¦®à¤ ®¢ã) ä®à¬ã (á¬. 2.1.) ¨ ª ®¨ç¥áªãî ä®à¬ã ä - §®¢®© ¯¥à¥¬¥®© (á¬. 2.2.), ª ª ¨¡®«¥¥ à á¯à®áâà ¥ë¥.
120
5.3.1.§®¢ë¥ ¯®àâà¥âë ¯à¨ ¤¨ £® «ì®© (¦®à¤ ®¢®©) ä®à- ¬¥ ¬ âà¨æë A
⮬ á«ãç ¥, ª®£¤ ¬ âà¨æ A ¯à¥¤áâ ¢«¥ ¢ ᮡá⢥®¬
¡ §¨á¥, ¯®áâ஥¨¥ ä §®¢ëå ¯®àâà¥â®¢ ¥áª®«ìª® ã¯à®é ¥â- áï. ¯à¨¬¥à, ¬®¦® ¯®«ãç¨âì ¤®áâ â®ç® ¯à®áâë¥ ä®à¬ã- «ë ¤«ï ä §®¢ëå ªà¨¢ëå. áᬮâਬ ®â¤¥«ì® á«ãç ¨ ¢¥é¥- á⢥ëå ¨ ¬¨¬ëå ᮡá⢥ëå ç¨á¥«.
1.¥é¥áâ¢¥ë¥ à §«¨çë¥ ª®à¨. §¥« ¨ ᥤ«®. ëè¥, ¢
¯.5.3. à áᬮâà¥ë å à ªâ¥àë¥ ¢¨¤ë ä §®¢ëå ¯®àâà¥â®¢,
¢ ⮬ ç¨á«¥ { ¨ ¯à¨ s1 s2 |
2 R |
|
s1 |
= 0 s2 |
= 0 s1 |
= s2: |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
6 |
6 |
|
â®ç¨¬ ¢¨¤ ä §®¢ëå ªà¨¢ëå ¯à¨ ¤¨ £® «ì®© ¬ âà¨æ¥ |
||||||||||||||||
A = diagfs1 s2g |
¤«ï í⮣® á«ãç ï. ª ®â¬¥ç¥® ¢ëè¥ (á¬. |
|||||||||||||||
3.1.1.), ¯à¨ ¢¥é¥á⢥ëå à §«¨çëå ª®àïå å à ªâ¥à¨áâ¨ç¥- |
||||||||||||||||
᪮£® ¬®£®ç«¥ |
|
¬ âà¨æë ¥¥ ᮡáâ¢¥ë¥ ¢¥ªâ®àë ¯à ¢«¥- |
||||||||||||||
ë ¢¤®«ì ®à⮣® «ìëå ª®®à¤¨ âëå ®á¥©. |
ਬ¥¬, çâ® |
|||||||||||||||
x1 = e = [1 0]T |
, x2 = e |
|
= [0 1]T : |
à ¢¥¨ï á®áâ®ï¨ï (5.1) |
||||||||||||
0 |
1 |
|
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
⮣¤ |
¯à¨¨¬ îâ ¢¨¤ |
|
|
|
|
|
|
|
|
|
|
|||||
|
< |
dx1 |
= s1x1 |
(t) x1 |
(0) = x1 0 |
|
|
|||||||||
|
|
|
dt |
|
(5.3) |
|||||||||||
|
8 |
|
|
|
||||||||||||
|
> dx2 |
= |
|
s2x2(t) |
x2(0) = x2 0: |
|
|
|||||||||
|
> |
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
᪫îç ï ¨§:(5.3) ¢à¥¬ï (íâ® ¬®¦® ᤥ« âì, ä®à¬ «ì® "¯®- |
||||||||||||||||
¤¥«¨¢" ¢â®à®¥ ãà ¢¥¨¥ ¯¥à¢®¥ á ãç¥â®¬ s1 |
= 0) ¯®«ã稬 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
¤¨ää¥à¥æ¨ «ì®¥ ãà ¢¥¨¥ á à §¤¥«ïî騬¨áï ¯¥à¥¬¥ë- |
||||||||||||||||
¬¨. ਨ¬ ï ¢ ª ç¥á⢥ à£ã¬¥â |
x1 ¯®«ã稬 ¢ëà ¦¥¨¥ |
|||||||||||||||
¤«ï x2 : |
|
|
|
dx2 |
|
s2x2 |
dx2 |
|
s2 |
dx1 |
|
|
||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
dx1 |
= s1x1 |
x2 |
= s1 |
x1 |
|
|
|||||
|
s2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lnjx2j = s1 lnjx1j |
+ C1 |
®âªã¤ |
®ª®ç â¥«ì® ¯®«ãç ¥¬ ¢ëà ¦¥- |
|||||||||||||
¨¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s2 |
|
|
|
|
|
|
|
|
|
j |
x2 |
j |
= C x1 |
j |
s1 |
(s1 |
= 0 |
x1 |
= 0): |
|
(5.4) |
||||
|
|
|
|
j |
|
|
6 |
|
|
6 |
|
|
||||
ëà ¦¥¨¥ (5.4) ®¯¨áë¢ ¥â «¨¨¨, |
ª®â®àëå à ᯮ«®¦¥ë |
|||||||||||||||
ä §®¢ë¥ ªà¨¢ë¥ ¢ 㪠§ ëå á«ãç ïå. ¬¥â¨¬, çâ® ¯à¨ ᮢ- ¯ ¤ îé¨å § ª å ᮡá⢥ëå ç¨á¥« í⨠ªà¨¢ë¥ ¨¬¥îâ ¢¨¤ "¯ à ¡®«", ¯à¨ à §ëå § ª å { "£¨¯¥à¡®«". ¥à¢ë© ¢¨¤ ä §®¢®£® ¯®àâà¥â ᮮ⢥âáâ¢ã¥â 㧫ã (ãá⮩稢®¬ã ¨«¨ ¥- ãá⮩稢®¬ã), ¢â®à®© { ᥤ«ã.
121
