
Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления
.pdf"ᮢ६¥ë¬". ¬¥â¨¬ â ª¦¥, çâ® ¢ ¨¦¥¥àãî ¯à ªâ¨- ªã ¢á¥ £«ã¡¦¥ ¯à®¨ª îâ ¬¥â®¤ë, ª®â®àë¥ à ¥¥ ª § «¨áì 㤥«®¬ ª« áá¨ç¥áª®© ¬ ⥬ ⨪¨ ¨ ¬¥å ¨ª¨. ®í⮬ã á«¥- ¤ã¥â £®¢®à¨âì ¥ ®¡ «ìâ¥à ⨢ëå, ® ¤®¯®«ïîé¨å ¤à㣠¤à㣠¯®¤å®¤ å. ®¤¨å á«ãç ïå ¡®«¥¥ 㤮¡ë¬ ï¥âáï ¨á¯®«ì§®¢ ¨¥ ¯¥à¥¤ â®çëå äãªæ¨©, ¢ ¤à㣨å { ãà ¢¥¨© á®áâ®ï¨ï, ¢® ¬®£¨å á«ãç ïå ¯à¨¬¥¥¨¥ ®¡®¨å ¯®¤å®¤®¢ à ¢®æ¥®.
ᮢ ï ç áâì ª¨£¨ (£« ¢ë 1 { 11) ᮤ¥à¦¨â ¤®áâ â®ç- ® ¯®«®¥ ¢¢¥¤¥¨¥ ¢ ¬¥â®¤ ¯à®áâà á⢠á®áâ®ï¨©, ¢ ¥£® ®á®¢ë¥ ¯®ïâ¨ï, ¨¤¥¨ ¨ १ã«ìâ âë. ।¯®« £ ¥âáï, çâ® ¯®á«¥ § ª®¬á⢠á í⮩ ç áâìî ç¨â ⥫ì ᬮ¦¥â ¯®¨¬ âì ï§ëª ãçëå áâ ⥩ ¨ ¬®®£à 䨩, ¢ ª®â®àëå ¤ ë© ¬¥â®¤ è¨à®ª® ¨á¯®«ì§ã¥âáï. «ï ¡®«¥¥ ¯®«®£® ¨§ãç¥¨ï ¢ ᮮ⢥â- áâ¢ãîé¨å ¬¥áâ å ⥪áâ ¤ ë ¡¨¡«¨®£à ä¨ç¥áª¨¥ 㪠§ ¨ï.®¤à®¡¥¥ ® ᮤ¥à¦ ¨¨ ª¨£¨ ¬®¦® 㧠âì ¨§ ®£« ¢«¥¨ï.
®¤¥а¦ ¨¥ ®б®¢®© з бв¨ ª¨£¨ б®®в¢¥вбв¢г¥в гз¥¡л¬ ¯« ¬ ªгаб®¢ в¥®а¨¨ ¢в®¬ в¨з¥бª®£® г¯а ¢«¥¨п ¯а¨ ¯®¤- £®в®¢ª¥ ¨¦¥¥а®¢ ¢ ®¡« бв¨ ¢в®¬ в¨§ ж¨¨ ¨ г¯а ¢«¥¨п.¤¥бм в¥¬ ¥ ¬¥¥¥ ®вбгвбв¢гов в ª¨¥ ¢ ¦л¥ а §¤¥«л, ª ª
¨áá«¥¤®¢ ¨¥ ãá⮩稢®á⨠«¨¥©ëå á¨á⥬ ®á®¢¥ «- £¥¡à ¨ç¥áª¨å ¨ ç áâ®âëå ªà¨â¥à¨¥¢, ¡®«¥¥ ⮣® { ¯®ï⨥ ãá⮩稢®á⨠áç¨â ¥âáï § ª®¬ë¬ ç¨â ⥫î (å®âï ¡ë ¨- âã¨â¨¢®¬ ã஢¥), ®¯à¥¤¥«¥¨ï ãá⮩稢®á⨠¤ ë 㦥 ¢ á¢ï§¨ á ¬¥â®¤®¬ äãªæ¨© ï¯ã®¢ ¯à¨ à áᬮâ२¨ ¥«¨- ¥©ëå á¨á⥬. ¥â ¬¥â®¤®¢ «¨§ â®ç®á⨠á¨á⥬ à¥-
£ã«¨à®¢ ¨ï ¨ ¬¥â®¤®¢ á¨â¥§ ª®à४â¨àãîé¨å §¢¥ì¥¢ ®á®¢¥ ç áâ®âëå å à ªâ¥à¨á⨪. ¥¤®áâ ⮪ ¬¥áâ ¥ ¯®§¢®- «¨« à áᬮâà¥âì ®¯¨á ¨¥ ¬®£®á¢ï§ëå ¤¨ ¬¨ç¥áª¨å á¨- á⥬ ãà ¢¥¨ï¬¨ ¢å®¤-¢ë室. ® ⮩ ¦¥ ¯à¨ç¨¥ ª¨£ á®- ¤¥à¦¨â ᢥ¤¥¨ï ⮫쪮 ® ¤¥â¥à¬¨¨à®¢ ëå á¨á⥬ å.
®®¡é¥ £®¢®àï, ª¨£ ¯®á¢ïé¥ ¥ ⮫쪮 á¨á⥬ ¬ ¢- ⮬ â¨ç¥áª®£® ã¯à ¢«¥¨ï, ® ¨ ¤¨ ¬¨ç¥áª¨¬ á¨á⥬ ¬ ¢®- ®¡é¥, ¡¥§®â®á¨â¥«ì® ª ⮬ã, ¨¬¥¥âáï ¢ ¨å ®¡à â ï á¢ï§ì ¨«¨ ¥â. ®«ì讥 ¢¨¬ ¨¥ 㤥«ï¥âáï ᯮᮡ ¬ ¯à¥®¡à §®- ¢ ¨ï ¬®¤¥«¥©, â ª¦¥ ¬¥â®¤ ¬ ⥮ਨ ®æ¥¨¢ ¨ï ¨ ¬®¤ «ì- ®£® ã¯à ¢«¥¨ï { í⨠¢ ¦ë¥ à §¤¥«ë ⥮ਨ ¤¨ ¬¨ç¥áª¨å á¨á⥬ ¥¤®áâ â®ç® ¯®«® ®á¢¥é¥ë ¢ ¤®áâ㯮© ã祡®© «¨â¥à âãà¥. «¨§ ¥«¨¥©ëå á¨á⥬ ᮤ¥à¦¨â âà ¤¨æ¨- ®ë¥ à §¤¥«ë, ®â®áï騥áï ª ¬¥â®¤ ¬ £ ମ¨ç¥áª®© «¨¥-
12
ਧ 樨 ¨ ¡á®«î⮩ ãá⮩稢®áâ¨, ¨ à áè¨à¥ ¢ ¯à - ¢«¥¨¨ ¨áá«¥¤®¢ ¨ï ᪮«ì§ïé¨å ०¨¬®¢.
®á«¥¤ïï ç áâì (£« ¢ë 12, 13) ®â®á¨âáï ª "¯¥à¥¤¥¬ã ªà î" 㪨 { ¬¥â®¤ ¬ ¥«¨¥©®£® ¨ ¤ ¯â¨¢®£® ã¯à ¢«¥- ¨ï, ¨â¥á¨¢® à §¢¨¢ ¢è¨¬áï ¢ 90-å £®¤ å. â®â ¬ â¥à¨ « ¨§«®¦¥ ¡®«¥¥ äà £¬¥â à®, ¥£® ®â¡®à ¢«¨ï«¨ ãçë¥ ¨â¥à¥áë ¢â®à®¢. ᮢ®¥ ¢¨¬ ¨¥ 㤥«ï¥âáï ¬¥â®¤ ¬ ¤ ¯â¨¢®£® ã¯à ¢«¥¨ï á ¥ï¢®© íâ «®®© ¬®¤¥«ìî ¨ ¬¥- ⮤ã èãâ¨à®¢ ¨ï, â ª¦¥ § ¤ ç ¬ ¨ ¬¥â®¤ ¬ ã¯à ¢«¥¨ï ª®«¥¡ ⥫ì묨 (¢ ⮬ ç¨á«¥ { å ®â¨ç¥áª¨¬¨) ¯à®æ¥áá ¬¨. áâ®ï饥 ¢à¥¬ï 㪠§ ë¥ ¢®¯à®áë á« ¡® ®á¢¥é¥ë ¥ ⮫ì- ª® ¢ ã祡¨ª å ¨ ¬®®£à ä¨ïå, ® ¨ ¢ ¦ãà «ìëå áâ âìïå. â® ¦¥ ¢à¥¬ï ªâã «ì®áâì ¯¥à¥ç¨á«¥ëå § ¤ ç à áâ¥â. ¨ ¯à¥¤áâ ¢«ïîâ ¨ ⥮à¥â¨ç¥áª¨© ¨â¥à¥á, ¯®áª®«ìªã á¢ï§ ë á ¨áá«¥¤®¢ ¨¥¬ ç áâ¨ç®© ãá⮩稢®á⨠¨ ç áâ¨ç®© áâ - ¡¨«¨§ 樨 ¥«¨¥©ëå á¨á⥬ { ¯à ¢«¥¨¥¬, ª®â®à®¥, ¯®- ¢¨¤¨¬®¬ã, ¡ã¤¥â ¨£à âì ¢ ¦ãî à®«ì ¢ à §¢¨â¨¨ ⥮ਨ ¢- ⮬ â¨ç¥áª®£® ã¯à ¢«¥¨ï ¢ ç «¥ XXI ¢¥ª .
«ï ¡®«¥¥ £«ã¡®ª®£® ¨§ã票ï ⥮ਨ ¥«¨¥©®£® ¨ ¤ - ¯â¨¢®£® ã¯à ¢«¥¨ï ¬®¦® ४®¬¥¤®¢ âì ª¨£ã . . ¨-
à®è¨ª , . . ¨ª¨ä®à®¢ , . . à ¤ª®¢ " ¥«¨¥©®¥ ¨ ¤ ¯â¨¢®¥ ã¯à ¢«¥¨¥ á«®¦ë¬¨ ¤¨ ¬¨ç¥áª¨¬¨ á¨á⥬ - ¬¨" [64], ¢ë室ïéãî ®¤®¢à¥¬¥® ¢ ⮩ ¦¥ á¥à¨¨.
¨£ á ¡¦¥ § ¤ ç ¬¨ ¨ ã¯à ¦¥¨ï¬¨. ਠ¯®¤¡®à¥ ã¯à ¦¥¨© ¢â®àë ¯®«ì§®¢ «¨áì å®à®è® ¨§¢¥áâ묨 ¨ ¯à®- 襤訬¨ ¨á¯ëâ ¨¥ ¢à¥¬¥¥¬ ª¨£ ¬¨ . . ¤à¥¥¢ [3],
. 㥡¥à£¥à |
[174], . ¢ ª¥à ª ¨ . ¨¢ [47], . |
î ¨ . ¥©¥à |
[94]. |
§¢¨â¨¥ ¢ëç¨á«¨â¥«ì®© â¥å¨ª¨ ¯à¥¤®¯à¥¤¥«¨«® ¥ ⮫ì- ª® «¨æ® ⥮ਨ ã¯à ¢«¥¨ï, ® ¨ ¬¥â®¤ë ¥¥ ¯à¥¯®¤ ¢ ¨ï.ª®æ¥ XX ¢¥ª ¥¢®§¬®¦® ¨§ãç âì ⥮à¨î, ¥ ¯®«ì§ãïáì ¯à®£à ¬¬ë¬¨ ¯ ª¥â ¬¨ ¨ á। ¬¨. ¨¡®«ì襥 à á¯à®- áâà ¥¨¥ ¢ ¯¥à¥¤®¢ëå ¢ëáè¨å ã祡ëå § ¢¥¤¥¨ïå è« ã¤®¡ ï ¨ 㨢¥àá «ì ï á¨á⥬ MATLABR, à §à ¡®â - ï ¨ ª®¬¬¥àç¥áª¨ à á¯à®áâà 塞 ï ä¨à¬®© The MathWorks Com., . ®í⮬㠨§«®¦¥¨¥ ¢ ¤ ®© ª¨£¥ ®à¨¥â¨- ஢ ® á¨á⥬ â¨ç¥áª®¥ ¨á¯®«ì§®¢ ¨¥ á¨á⥬ë MATLAB ¤«ï à¥è¥¨ï § ¤ ç «¨§ ¨ á¨â¥§ . ¥ª®â®àë¥ ¢á¯®¬®£ - ⥫ìë¥ á¢¥¤¥¨ï ® á¨á⥬¥ MATLAB ¯®¬¥é¥ë ¢ ਫ®¦¥- ¨¨ C. ®¯®«¨â¥«ìãî ¨ä®à¬ æ¨î ¬®¦® ©â¨ ¢ ª¨£ å
13
[10, 32, 81, 82], â ª¦¥ á ©â¥ ä¨à¬ë The MathWorks Com.
(www.mathworks.com).
¨â â¥«ï ¢¥àïª § ¨â¥à¥áã¥â ¯®å®¦ ï MATLAB, ® ¢ ®â«¨ç¨¥ ®â ¤ ®© á¨á⥬ë ᢮¡®¤® à á¯à®áâà ï¥- ¬ ï á¨á⥬ ScilabR, à §à ¡®â ï ¢® à 樨 ¢ ¨áâ¨âã⥠INRIA (www-rocq.inria.fr/scilab). à ⪨¥ ᢥ¤¥¨ï ® á¨áâ¥- ¬¥ ScilabR ¯à¨¢¥¤¥ë ¢ ਫ®¦¥¨¨ D.
¨£ ¬®¦¥â ¨á¯®«ì§®¢ âìáï ¢ ª ç¥á⢥ ã祡®£® ¯®á®¡¨ï ¯à¥¯®¤ ¢ ⥫ﬨ, áâ㤥⠬¨ ¨ ᯨà â ¬¨ ¯® á¯¥æ¨ «ì®-
áâï¬, á¢ï§ ë¬ á ¢â®¬ ⨧ 樥© ¨ ã¯à ¢«¥¨¥¬ â ª¦¥ á¯¥æ¨ «¨áâ ¬¨, ¨â¥à¥áãî騬¨áï ¯à¨«®¦¥¨ï¬¨ ⥮ਨ ¤¨- ¬¨ç¥áª¨å á¨á⥬.
¢â®àë ᮧ îâ «¨ç¨¥ ¥¤®áâ ⪮¢ ¢ à ¡®â¥ ¨ á ¡« - £®¤ à®áâìî ¯à¨¬ãâ «î¡ãî ªà¨â¨ªã, ¢ ⮬ ç¨á«¥ ¨ á ¬ãî ª®áâàãªâ¨¢ãî { ¯¨á ¨¥ ¤à㣮© ª¨£¨ ¯®¤®¡®£® த .¬¥ç¥ë¥ ®¯¥ç ⪨ ¨ ¤®¯®«¨â¥«ìë© ¬ â¥à¨ « ¯® ⥬¥ ª¨£¨ ¡ã¤¥â ¯®¬¥é âìáï ¢ â¥à¥â áâà ¨æ¥ « ¡®à - â®à¨¨ " ¯à ¢«¥¨¥ á«®¦ë¬¨ á¨á⥬ ¬¨" (www.ipme.ru/ipme/labs/ccs/ccs.html). ¬ ¬®¦® ©â¨
¨ ¤à㣨¥ ¯®«¥§ë¥ ᢥ¤¥¨ï ® ¯ã¡«¨ª æ¨ïå, ª®ä¥à¥æ¨ïå,
¯à®£à ¬¬ëå ¯à®¤ãªâ å, â ª¦¥ áá뫪¨ ¤à㣨¥ ¨áâ®ç- ¨ª¨ ¨ä®à¬ 樨 ¯® ⥮ਨ ¢â®¬ â¨ç¥áª®£® ã¯à ¢«¥¨ï ¨ ᬥ¦ë¬ ¢®¯à®á ¬.
§¤ ¨¥ ª¨£¨ ¡ë«® ¯®¤¤¥à¦ ® " ⥣à æ¨ï", ¯à®- ¥ªâ 360-01. ï¤ à¥§ã«ìâ ⮢, ¯®¬¥é¥ëå ¢ ¥¥, ¡ë« ¯®«ãç¥ ¢ ¯à®æ¥áᥠᮢ¬¥á⮩ à ¡®âë ¢â®à®¢ ¯® £à â ¬ (96-
01-01151, 99-01-0672) ¨ " ⥣à æ¨ï" (¯à®¥ªâë 2.1-589,0145, 0151) ¢ áâ¨âã⥠¯à®¡«¥¬ ¬ 訮¢¥¤¥¨ï .
¢в®ал ¯®«м§говбп б«гз ¥¬ ¯®¡« £®¤ а¨вм ¢б¥е, ¯®¬®- £ ¢и¨е ¨¬ ¢ а ¡®в¥ ¤ ª¨£®©, в ª¦¥ ¢ла §¨вм ¯а¨§ - в¥«м®бвм а¥ж¥§¥в ¬ . . ¥¬«пª®¢г ¨ . . «ли¥¢г § ¯®«¥§л¥ ¨ ¤®¡а®¦¥« в¥«мл¥ § ¬¥з ¨п.
¢â®àë ¯®á¢ïé îâ ª¨£ã ¯ ¬ï⨠¡¥§¢à¥¬¥® ã襤襣®. . ¥à¢®§¢ ᪮£® { ¡«¥áâï饣® ã祮£® ¨ ¯¥¤ £®£ , 祩 ä㤠¬¥â «ìë© " ãàá ⥮ਨ ¢â®¬ â¨ç¥áª®£® ã¯à ¢«¥- ¨ï" [76] ¡ë« ¨ ®áâ ¥âáï ¥¤®áï£ ¥¬ë¬ ¯à¨¬¥à®¬ ¤«ï ¯®¤à - ¦ ¨ï.
®à¨á ¤à¨¥¢áª¨©, «¥ªá ¤à à ¤ª®¢ªâ- ¥â¥à¡ãà£, ¤¥ª ¡àì 1999 £.
14

1. .
1.1.¨ ¬¨ç¥áª¨¥ ¨ áâ â¨ç¥áª¨¥ á¨á⥬ë. ®ï⨥ á®áâ®ï¨ï ¤¨ ¬¨ç¥áª¨å á¨á⥬
î¡ ï á¨á⥬ , ¢ ⮬ ç¨á«¥ ¨ á¨á⥬ ã¯à ¢«¥¨ï, á®áâ®- ¨â ¨§ ᮢ®ªã¯®á⨠¯®¤á¨á⥬ (§¢¥ì¥¢). ¢¥ìï ¬®£ãâ à §- «¨ç âìáï ¯® å à ªâ¥àã ॠªæ¨© ¢å®¤®¥ ¢®§¤¥©á⢨¥. í⮩ â®çª¨ §à¥¨ï ¢á¥ §¢¥ìï ¬®£ãâ ¡ëâì à §¤¥«¥ë áâ -
â¨ç¥áª¨¥ (¡¥§ë¥à樮ë¥) ¨ ¤¨ ¬¨ç¥áª¨¥ (¨¥à樮ë¥) .áᬮâਬ ®â«¨ç¨â¥«ìë¥ ®á®¡¥®á⨠¢ ¯®¢¥¤¥¨¨ ¨ ¬ â¥-
¬â¨ç¥áª®¬ ®¯¨á ¨¨ á¨á⥬ ®¤®£® ¨ ¤à㣮£® ⨯®¢.
â â¨ç¥áª¨¥ á¨á⥬ë 1 ®¡« ¤ îâ ¬£®¢¥®© ॠªæ¨¥©
¢å®¤®¥ ¢®§¤¥©á⢨¥. ®«¥¥ áãé¥áâ¢¥ë¬ á¢®©á⢮¬ â ª¨å á¨á⥬ ï¥âáï â®, çâ® ¨å ॠªæ¨ï ¢å®¤®¥ ¢®§¤¥©á⢨¥ ¥ § ¢¨á¨â ®â ¯à¥¤ëáâ®à¨¨, ®â ¯®¢¥¤¥¨ï á¨áâ¥¬ë ¢ ¯à®è«®¬,
⪦¥ ®â ¯à¥¤ë¤ãé¨å § 票© ¢å®¤ .
⥬ â¨ç¥áª¨ íâ® ¬®¦® ®¯¨á âì á«¥¤ãî騬 ®¡à §®¬.
¡®§ 稬 ç¥à¥§ u(t) y(t) ¢å®¤ ¨ ¢ë室 á¨áâ¥¬ë ¢ ¬®¬¥â t: áâ â¨ç¥áª®© á¨áâ¥¬ë ¤«ï ª ¦¤®£® t ¢ë室 y(t) ¬®¦® ®¯à¥¤¥«¨âì ®¤®§ ç® ¯® § 票î u(t) ¢ â®â ¦¥ ¬®¬¥â ¢à¥¬¥¨. «ï í⮩ 楫¨ á«ã¦¨â áâ â¨ç¥áª ï å à ªâ¥à¨áâ¨-
ªy = f (u) ¨«¨ y = f (u t) (¤«ï ¥áâ 樮 àëå á¨á⥬).
ᮮ⢥âá⢨¨ á ¥© ¯®«ãç ¥¬ y(t) = f (u(t)): ¨ª ª®© ¤à㣮© ¤®¯®«¨â¥«ì®© ¨ä®à¬ 樨 ¥ âॡã¥âáï. 2
ç¥ ®¡á⮨⠤¥«® á ¤¨ ¬¨ç¥áª¨¬¨ á¨á⥬ ¬¨. å ®á®- ¡¥®áâìî ï¥âáï â®, çâ® ¤«ï ®¯à¥¤¥«¥¨ï y(t) ¥¤®áâ â®ç- ® ¨ä®à¬ 樨 ®¡ u(t) ¢ â®â ¦¥ ¬®¬¥â ¢à¥¬¥¨. ë室®© ᨣ « § ¢¨á¨â â ª¦¥ ®â ¯à¥¤ëáâ®à¨¨ ¨§¬¥¥¨ï ¢å®¤ ¨, ªà®¬¥ ⮣®, ᮢ®ªã¯®á⨠¥ª®â®àëå ¢¥«¨ç¨, §ë¢ ¥¬ëå ç «ìë¬ á®áâ®ï¨¥¬ á¨á⥬ë. áᬮâਬ ¯®ï⨥ á®áâ®- ï¨ï ¡®«¥¥ ¯®¤à®¡®.
®ï⨥ á®áâ®ï¨ï á¨á⥬ë (§¢¥ ) ï¥âáï ®¤¨¬ ¨§
¡§®¢ëå ¯®ï⨩ ⥮ਨ ¤¨ ¬¨ç¥áª¨å á¨á⥬, ¯®í⮬㠮®
1 ¤ «ì¥©è¥¬ â¥à¬¨ë á¨á⥬ , ¯®¤á¨á⥬ ¨ §¢¥® ®¡ëç® ¡ã- ¤ã⠨ᯮ«ì§®¢ âìáï ª ª ᨮ¨¬ë, â ª ª ª ¨å ¬ ⥬ â¨ç¥áª¨¥ ¬®¤¥«¨
®¤®â¨¯ë.
2 â â¨ç¥áª®© å à ªâ¥à¨á⨪®© ¢ ®¡é¥¬ á«ãç ¥ §ë¢ îâ § ¢¨á¨- ¬®áâì ¬¥¦¤ã ¢å®¤®¬ ¨ ¢ë室®¬ á¨áâ¥¬ë ¢ ãáâ ®¢¨¢è¥¬áï ०¨¬¥ (¯® ¨áâ¥ç¥¨¨ ¢à¥¬¥¨ ¯¥à¥å®¤ëå ¯à®æ¥áᮢ). ®¦® ᪠§ âì, çâ® ã ¡¥§ë- ¥à樮ëå á¨á⥬ (§¢¥ì¥¢) íâ®â ०¨¬ áâ㯠¥â ¥¬¥¤«¥®.
15

®¯à¥¤¥«ï¥âáï ¥ ç¥à¥§ ¤à㣨¥ ¯®ïâ¨ï, ªá¨®¬ â¨ç¥áª¨ { ¯¥à¥ç¨á«¥¨¥¬ ᮢ®ªã¯®á⨠¯à¨áãé¨å ¥¬ã ᢮©á⢠[44, 46].
áᬮâਬ ¥ª®â®àë¥ ¨§ ¨å.
ª ®â¬¥ç¥® ¢ëè¥, ¢ë室 ¤¨ ¬¨ç¥áª®© á¨áâ¥¬ë ®¯à¥- ¤¥«ï¥âáï ®¤®§ ç®, ¥á«¨ § ¤ ë ¯à¥¤ëáâ®à¨ï ¨§¬¥¥¨ï ¢å®¤®£® ¯à®æ¥áá ¥ª®â®à®¬ ¯à®¬¥¦ã⪥ ¨, ªà®¬¥ ⮣®, ¥ª®â®à ï ᮢ®ªã¯®áâì ¢¥«¨ç¨, ®â®áïé ïáï ª ç «ã ¤ - ®£® ¯à®¬¥¦ã⪠{ ç «ì®¥ á®áâ®ï¨¥ á¨á⥬ë. ¨¬¢®«¨- ç¥áª¨ íâ® ¡ã¤¥¬ § ¯¨áë¢ âì â ª: 3
y(t1) = S(x(t0 )\ u[t0 t1]):
ª¨¬ ®¡à §®¬, á®áâ®ï¨¥ á¨á⥬ë { íâ® ¥ª®â®àë© ¯ à - ¬¥âà, ¯®§¢®«ïî騩 ᤥ« âì ®¤®§ çë¬ ®¯à¥¤¥«¥¨¥ ¥¥ ¢ë- 室 ¯® ¢å®¤ã.
§«¨çë¥ ç «ìë¥ á®áâ®ï¨ï ¯à¨¢®¤ïâ, ¢®®¡é¥ £®¢®àï,
ªà §«¨ç®© ॠªæ¨¨ ®¤® ¨ â® ¦¥ ¢å®¤®¥ ¢®§¤¥©á⢨¥. ¯à¨¢¥¤¥®¬ ¢ëè¥ ãà ¢¥¨¨ S { ¥ª®â®àë© ®¯¥à â®à, ¯à¥- ®¡à §ãî騩 ®¤ã äãªæ¨î ¢ ¤àã£ãî.
®áâ®ï¨¥ á¨áâ¥¬ë ¤®«¦® 㤮¢«¥â¢®àïâì ç¥âë६ ªá¨®- ¬ ¬ (ãá«®¢¨ï¬) ᮢ¬¥áâ®á⨠[44]. áᬮâਬ ¤¢¥ ¨¡®«¥¥
¢ ¦ë¥ ¨§ ¨å. |
|
ªá¨®¬ 1. ë室 y(t) ¤«ï ¢á¥å t t0 ®¯à¥¤¥«ï¥âáï ®¤- |
|
®§ ç®, ¥á«¨ § |
¤ ë x(t0 ) ¨ u[t0 t1] (á¬. à¨á. 1.1, ). |
ª¨¬ ®¡à §®¬, á®áâ®ï¨¥ á¨áâ¥¬ë ¢ ¤ ë© ¬®¬¥â ¢à¥- |
|
¬¥¨ ᮤ¥à¦¨â |
¢áî ¯ ¬ïâì ® ¯à®è«®¬, áãé¥á⢥ãî ¤«ï |
à §¢¨â¨ï ¯à®æ¥áá ¢ ¡ã¤ã饬. ᫨ 䨪á¨à®¢ âì ç «ì®¥ á®áâ®ï¨¥, â® ¡ã¤ã饥 ®â ¯à®è«®£® ¥ § ¢¨á¨â\ ¢á¥, çâ® ã¦-
® § âì ®â ¯à®è«®£® ¤«ï ®¯à¥¤¥«¥¨ï ¯à®æ¥áá ¢ ¡ã¤ã饬, ᮤ¥à¦¨âáï ¢ á®áâ®ï¨¨ ¤ ë© ¬®¬¥â ¢à¥¬¥¨. ª¨¬ ®¡à §®¬, ¤«ï ®¯à¥¤¥«¥¨ï ¡ã¤ã饣® ¯®¢¥¤¥¨ï á¨áâ¥¬ë ¥ ¨¬¥¥â § 票ï â®, ª ª ® ¯à¨è« ¢ ¤ ®¥ á®áâ®ï¨¥, { ¯®
ç «ì®¬ã á®áâ®ï¨î ¨ ¢å®¤ã ¯à®æ¥áá ®¯à¥¤¥«ï¥âáï ®¤®- § ç®.
ªá¨®¬ 2. ᫨ âà ¥ªâ®à¨î á¨á⥬ë à §¡¨âì àï¤ ãç á⪮¢, â® ¬®¦® à áᬠâਢ âì ¤¢¨¦¥¨¥ ª ¦¤®¬ ¨§ ¨å ª ª ®¢ãî âà ¥ªâ®à¨î ¯à¨ ᮮ⢥âáâ¢ãî饬 ç «ì®¬ á®áâ®ï¨¨ (á¬. à¨á. 1.1, ¡).
ãáâì t0 < t1 < t2: ®£¤ y(t2) = S(x(t0 )\ u[t0 t2]): ¤à㣮© áâ®à®ë, ¯à¨ «î¡ëå x(t0) u[t0 t1] ¬®¦® ®¯à¥¤¥«¨âì á®áâ®ï¨¥
3 ¥à¥§ u[t0t1] ®¡®§ 祮 á㦥¨¥ äãªæ¨¨ u( ) ¯à®¬¥¦ã⮪ [t0 t1]:
16
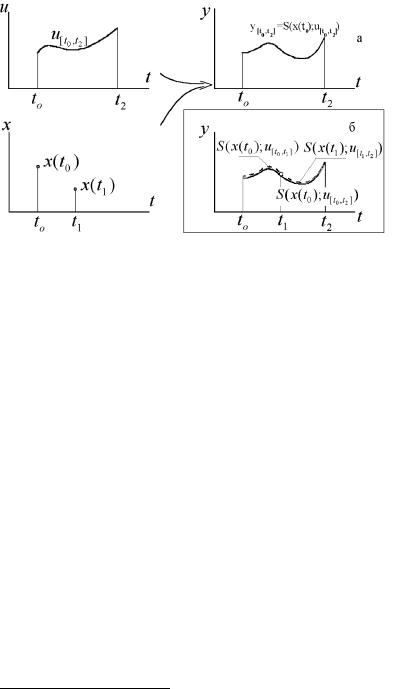
¨á. 1.1. ªá¨®¬ë ᮢ¬¥áâ®áâ¨. |
|
x(t1) â ª¨¬ ®¡à §®¬, çâ® y(t2) = S(x(t1 )\ u[t1 t2 |
]): |
§ í⮩ ªá¨®¬ë á«¥¤ã¥â, çâ® á®áâ®ï¨¥ |
¤¨ ¬¨ç¥áª®© |
б¨бв¥¬л ¤®«¦® ¨§¬¥пвмбп ¢® ¢а¥¬¥¨ б®®в¢¥вбв¢гой¨¬ ®¡а §®¬ (¢ § ¢¨б¨¬®бв¨ ®в ¢е®¤®£® ¯а®ж¥бб ¨ з «м®£® б®бв®п¨п).
¯à¥¤¥«¥¨¥.
®¦¥á⢮ X = fxg ¢®§¬®¦ëå § 票© á®áâ®ï¨ï á¨áâ¥¬ë §ë¢ ¥âáï ¯à®áâà á⢮¬ á®áâ®ï¨©
(¤ ®© á¨á⥬ë). 4 2
áâ® ¬®¦® à áᬠâਢ âì ¢ ª ç¥á⢥ ¯à®áâà á⢠á®- áâ®ï¨© n-¬¥à®¥ «¨¥©®¥ ¢¥é¥á⢥®¥ ¯à®áâà á⢮, X = Rn: ®£¤ á®áâ®ï¨¥ x(t) ¥áâì n-¬¥àë© ¢¥é¥áâ¢¥ë© ¢¥ªâ®à { ¢¥ªâ®à á®áâ®ï¨ï, ¨«¨ ä §®¢ë© ¢¥ªâ®à. ®¬¯®¥âë í⮣®
¢¥ªâ®à ®¡ëç® ¡ã¤¥¬ ®¡®§ ç âì ç¥à¥§ xi(t) â.¥. ¯¨á âì
2 x1(t) 3
( ) x(t) = 6 x2.t 7 :
4 xn(t)5
«ï ªà ⪮á⨠¡ã¤¥¬ â ª¦¥ ¨á¯®«ì§®¢ âì § ¯¨áì
x = colfx1 x2 : : : xng ¨«¨ x = [x1 x2 : : : xn]T :
4 ᯮ«ì§ã¥âáï â ª¦¥ â¥à¬¨ "ä §®¢®¥ ¯à®áâà á⢮".
17
ª ï § ¯¨áì ¢ ®¡é¥¬ á«ãç ¥ ®§ ç ¥â, çâ® x ¥áâì ¢¥ªâ®à- á⮫¡¥æ, á®áâ ¢«¥ë© ¨§ à ᯮ«®¦¥ëå ¢ á⮫¡¥æ ª®¬¯®- ¥â ¢¥ªâ®à®¢ xi i = 1 2 : : : n : ®£¤ , ª ª ¡ã¤¥â ¢¨¤® ¨§ ª®â¥ªáâ , ¨¤¥ªá ¨á¯®«ì§ã¥âáï ¤«ï ®¡®§ 票ï à §«¨çëå ®¤®¨¬¥ëå ¢¥ªâ®à®¢.
¬¥â¨¬, çâ® â ª®© ¢¨¤ ¯à®áâà á⢠á®áâ®ï¨© ¥ ¨áç¥à- ¯ë¢ ¥â ¢á¥å ¢®§¬®¦ëå á¨âã 権. ¯à¨¬¥à, ¯à®áâà á⢮ á®áâ®ï¨© ª®¥çëå ¢â®¬ ⮢ á®á⮨⠨§ ª®¥ç®£® ç¨á« â®ç¥ª. ¤à㣮© áâ®à®ë, ¤«ï ¬®£¨å á¨á⥬ ¥«ì§ï 㪠§ âì ª®¥ç®¥ § 票¥ n à §¬¥à®á⨠¯à®áâà á⢠X: в ª¨¬ б¨бв¥¬ ¬ ®в®бпвбп а §«¨зл¥ а б¯а¥¤¥«¥л¥ ®¡к¥ªвл, ¤¨- ¬¨ª ª®в®але ®¯¨бл¢ ¥вбп ¤¨дд¥а¥ж¨ «мл¬¨ га ¢¥¨- п¬¨ ¢ з бвле ¯а®¨§¢®¤ле, ®¡к¥ªвл б § ¯ §¤л¢ ¨¥¬ ¨ в ª ¤ «¥¥. нв®© ª¨£¥ а бб¬ ва¨¢ овбп в®«мª® ª®¥ç®¬¥àë¥ ¤¨ ¬¨ç¥áª¨¥ á¨á⥬ë. ¤ ª® ¨ ¤«ï ª®¥ç®¬¥àëå á¨á⥬ ¥ ®¡ï§ â¥«ì® X = Rn: ¯à¨¬¥à, ¤«ï ¯à®á⥩襩 ¬¥å ¨- ç¥áª®© á¨á⥬ë { ¬ ï⨪ { ®¤®© ¨§ ¯¥à¥¬¥ëå á®áâ®ï¨ï ï¥âáï 㣮« ¯®¢®à®â ®â®á¨â¥«ì® â®çª¨ ¯®¤¢¥á . ® ¢ ¬®¦¥á⢥ ¢®§¬®¦ëå § 票© 㣫®¢®© ¯¥à¥¬¥®© â®çª¨ 0 à ¤. ¨ 2 à ¤. ᮢ¯ ¤ îâ. «¥¤®¢ ⥫ì®, íâ® ¬®¦¥á⢮
¥ ¬®¦¥â ¡ëâì «¨¥©ë¬ ¯à®áâà á⢮¬, ¥£® £¥®¬¥âà¨ç¥áª¨¬ ®¡à §®¬ ï¥âáï ¥ ¯àï¬ ï, ®ªà㦮áâì. âண®¥ à á- ᬮâ२¥ â ª¨å á¨á⥬ âॡã¥â ¯à¨¢«¥ç¥¨ï ¯®ïâ¨ï ¬®£®- ®¡à §¨ï ¨ ¢ë室¨â § à ¬ª¨ í⮩ ª¨£¨. ¥¬ ¥ ¬¥¥¥ ¬®£¨¥ ᢮©á⢠á¨á⥬ á 㣫®¢ë¬¨ ª®®à¤¨ â ¬¨ ¬®¦® ¨§ãç âì, ¥ ¨á¯®«ì§ãï ªá¨®¬ «¨¥©®£® ¯à®áâà á⢠. ®í⮬ã, ¥á«¨ ¥
®£®¢®à¥® ¯à®â¨¢®¥, ¬ë ¡ã¤¥¬ áç¨â âì, çâ® X = Rn: |
|||
§ |
®¯à¥¤¥«¥¨ï ¯®ïâ¨ï á®áâ®ï¨ï á«¥¤ã¥â, çâ® ¥á«¨ x |
||
{ á®áâ®ï¨¥ á¨á⥬ë, ( |
) { ¥ª®â®à®¥ ¢§ ¨¬® ®¤®§ 箥 |
||
|
|
|
|
®â®¡à |
¦¥¨¥ ¯à®áâà á⢠|
X ¢ ᥡï ( : X ;! X), â® x~ = (x) |
|
â ª¦¥ ¬®¦® à áᬠâਢ âì ª ª á®áâ®ï¨¥ ¤ ®© á¨á⥬ë
[44]. ª¨¬ ®¡à §®¬, á®áâ®ï¨¥ ®¯à¥¤¥«ï¥âáï ¥¥¤¨á⢥- ë¬ ®¡à §®¬, á â®ç®áâìî ¤® ¢§ ¨¬® ®¤®§ 箣® ¯à¥- ®¡à §®¢ ¨ï (ª®â®àëå ¬®¦¥â ¡ëâì ᪮«ì 㣮¤® ¬®£®).
ç áâ®áâ¨, ¥á«¨ |
X |
= Rn |
T { ¥ª®â®à ï ¥¢ë஦¤¥ ï |
¬ âà¨æ ¯®à浪 |
n |
(det T |
= 0) â® ¢¥ªâ®à x~ = T x â ª¦¥ ¬®- |
6
¦¥â ¡ëâì ¨á¯®«ì§®¢ ¤«ï ®¯¨á ¨ï á®áâ®ï¨ï á¨á⥬ë. -
ª®© ¯¥à¥å®¤ §ë¢ ¥âáï ¯à¥®¡à §®¢ ¨¥¬ ¡ §¨á ¢ ¯à®áâà - á⢥ á®áâ®ï¨©. â® ¯à¥®¡à §®¢ ¨¥ ¥ àãè ¥â ¢å®¤®- ¢ë室ëå á®®â®è¥¨© ¢ ®¯¨á ¨¨ á¨á⥬ë.
18

®ªà¥â¨§¨à㥬 ¢¨¤ ãà ¢¥¨© á®áâ®ï¨ï. áᬮâਬ â ª §ë¢ ¥¬ë¥ ª®¥ç®¬¥àë¥ ¤¨ää¥à¥æ¨ «ìë¥ (¥¯à¥àë¢- ë¥) á¨á⥬ë. à ¢¥¨ï á®áâ®ï¨ï â ª¨å á¨á⥬ ¬®£ãâ ¡ëâì ¯à¥¤áâ ¢«¥ë ¢ ¢¨¤¥
x(t) = |
f x(t) u(t) t x(t0 ) = x0 t |
|
t0 |
|
|
y(t) = |
g |
;x(t) u(t) t : |
|
(1.1) |
|
¥à¢®¥ ¨§ íâ¨å |
;ãà ¢¥¨© { (ᮡá⢥®) ãà ¢¥¨¥ á®áâ®- |
||||
ï¨ï, ¨«¨ í¢®«î樮®¥ ãà ¢¥¨¥, ®¯¨áë¢ ¥â ¨§¬¥¥¨¥ á®- áâ®ï¨ï á¨áâ¥¬ë ¢® ¢à¥¬¥¨ t 2 R ¢ § ¢¨á¨¬®á⨠®â ç «ì- ëå ãá«®¢¨© ¢ ¬®¬¥â t0 ¨ ¢å®¤®£® ¢®§¤¥©á⢨ï u(t): â®à®¥ ãà ¢¥¨¥ { ãà ¢¥¨¥ ¢ë室 , ãáâ ¢«¨¢ ¥â á¢ï§ì ¬¥¦¤ã â¥-
ªã騬¨ § 票ﬨ á®áâ®ï¨ï ¨ ¢å®¤ , á ®¤®© áâ®à®ë, ¨
¢ë室 |
y(t) { á ¤à㣮©. ªâ¨ç¥áª¨ ¢áï ¤¨ ¬¨ª á¨á⥬ë |
|||||
á®á।®â®ç¥ ¢ ¯¥à¢®¬ ãà ¢¥¨¨, |
¢â®à®¥ ï¥âáï áâ â¨- |
|||||
ç¥áª¨¬ á®®â®è¥¨¥¬. |
|
|
|
|
||
¥à¥¬¥ë¥, ¢å®¤ï騥 ¢ ãà ¢¥¨ï (1.1), áç¨â îâáï ¢¥ª- |
||||||
â®à묨: x(t) 2 Rn |
y(t) 2 Rl u(t) 2 Rm |
f( ) g( ) { ¢¥ªâ®à- |
||||
äãªæ¨¨ ®â ¢¥ªâ®àëå à£ã¬¥â®¢ ᮮ⢥âáâ¢ãîé¨å à §¬¥à- |
||||||
®á⥩. |
|
|
|
|
|
|
1.2. |
à ¢¥¨ï á®áâ®ï¨ï «¨¥©ëå á¨á⥬ |
|
||||
᫨ äãªæ¨¨ f ( ) g( ) «¨¥©ë ¯® x |
u â® ãà ¢¥¨ï á®- |
|||||
áâ®ï¨ï (1.1) ¬®£ãâ ¡ëâì § ¯¨á ë ¢ ¢¨¤¥ [44] |
|
|||||
|
x(t) = A(t)x(t) + B(t)u(t) |
x(t0) = x0 t t0 |
(1.2) |
|||
|
y(t) = C(t)x(t) + D(t)u(t): |
|
|
|
|
|
ª¨¥ á¨áâ¥¬ë §ë¢ îâáï ¥¯à¥àë¢ë¬¨ «¨¥©ë¬¨ á¨- |
||||||
á⥬ ¬¨. 5 ¤¥áì, ª ª ¨ ¢ëè¥, x(t) |
2 Rn |
y(t)2 Rl u(t) 2Rm |
||||
¬ âà¨æë-äãªæ¨¨ A(t) B(t) |
C(t) D(t) ¨¬¥îâ à §¬¥àë |
|||||
n n n m l n l m |
ᮮ⢥âá⢥®. |
|
|
|
||
¯à¥¤¥«¥¨¥ 1. |
᫨ D(t) |
0 â® â® á¨á⥬ (1.2) §ë¢ - |
||||
¥âáï ᮡá⢥®© (áâண® ॠ«¨§ã¥¬®©). ¯à®â¨¢®¬ á«ãç ¥ |
||||||
á¨á⥬ §ë¢ ¥âáï ¥á®¡á⢥®©. |
2 |
|
|
|||
5 «ï «¨¥©ëå á¨á⥬ á¯à ¢¥¤«¨¢ ¯à¨æ¨¯ á㯥௮§¨æ¨¨, ᮣ« á® ª®â®à®¬ã ॠªæ¨ï á¨áâ¥¬ë «¨¥©ãî ª®¬¡¨ æ¨î (á㯥௮§¨æ¨î) ¢®§- ¤¥©á⢨© ᮢ¯ ¤ ¥â á ⮩ ¦¥ «¨¥©®© ª®¬¡¨ 樥© ॠªæ¨© ª ¦¤®¥ ¢®§¤¥©á⢨¥ ¢ ®â¤¥«ì®áâ¨. ¡é¥¥ ®¯à¥¤¥«¥¨¥ «¨¥©ëå ¤¨ ¬¨ç¥áª¨å á¨á⥬ ¯à¨¢¥¤¥® ¢ ¯. 10.3.1. á. 231.
19
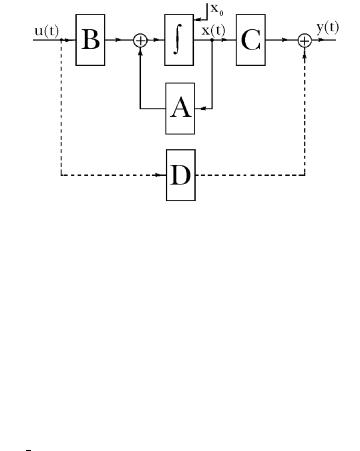
а ¢¥¨п б®бв®п¨п (1.2) а¥ «¨§г¥¬ле ¥¯а¥ал¢ле б¨- бв¥¬ ¨««обва¨аговбп бвагªвга®© бе¥¬®©, ¯а¨¢¥¤¥®©
à¨á. 1.2.
¨á. 1.2. âàãªâãà ï á奬 á¨á⥬ë (1.2).
¯à¥¤¥«¥¨¥ 2. ᫨ ¬ âà¨æë A(t) B(t) C(t) D(t) ¯®áâ®- ïë (¥ § ¢¨áï⠮⠢६¥¨ t), â® á¨á⥬ (1.2) §ë¢ ¥âáï
áâ 樮 ன, ¢ ¯à®â¨¢®¬ á«ãç ¥ { ¥áâ 樮 ன. 2
¨¤ ¯à®æ¥áᮢ ¢ áâ 樮 àëå á¨á⥬ å ¥ § ¢¨á¨â ®â â®- £®, ª ª®© ¬®¬¥â ¢à¥¬¥¨ à áᬠâਢ ¥âáï ª ª ç «ìë©.®í⮬㠤«ï ¨å ¬®¦® áç¨â âì t0 = 0:
®áª®«ìªã ¨¦¥ ®á®¢®¥ ¢¨¬ ¨¥ 㤥«ï¥âáï áâ 樮 à- ë¬ á®¡áâ¢¥ë¬ á¨á⥬ ¬, § ¯¨è¥¬ ᮮ⢥âáâ¢ãî騥 ãà ¢- ¥¨ï á®áâ®ï¨ï:
x(t) = Ax(t) + Bu(t) y(t) = Cx(t) x(0) = x0 t 0: (1.3)
«®£¨ç® ¬®£ãâ ¡ëâì § ¯¨á ë ãà ¢¥¨ï á®áâ®ï¨ï à¥- «¨§ã¥¬ëå ¤¨áªà¥âëå á¨á⥬. ¨ ¨¬¥îâ ¢¨¤ à §®áâëå
ãà ¢¥¨©
x[k + 1] = |
f x[k] u[k] k x[k0] = x0 k k0 |
|
|||
|
; |
|
|
|
|
y[k] = |
g;x[k |
] u[k] k |
(1.4) |
||
{ ¤«ï ¥«¨¥©ëå á¨á⥬ ¨ |
|
|
|
||
x[k + 1] = A[k]x[k] + B[k]u[k] |
x[t0] = x0 k k0 |
(1.5) |
|||
y[k] = C[k]x[k] + D[k]u[k] |
|
|
|||
|
|
|
20 |
|
|

{ ¤«ï «¨¥©ëå á¨á⥬. ãà ¢¥¨ïå (1.4), (1.5) k = k0 k0 + |
|||||||||||||
+1 k0 + 2 : : : { "¤¨áªà¥â®¥ ¢à¥¬ï", x[k] |
n y[k] |
2R |
l u[k] |
2 |
|||||||||
R |
m |
|
f ( )2R |
n |
g( ) |
2R |
l |
|
|
2 R |
|
||
|
|
|
|
: |
âà¨æë-äãªæ¨¨ A[k] B[k] C[k] D[k] |
||||||||
¨¬¥îâ à §¬¥àë n n n m l n l m: |
|
|
|
|
|||||||||
|
|
¬ ¥ ç ¨ ¥ . ®£¤ |
ãà ¢¥¨ï á®áâ®ï¨ï § ¯¨áë¢ îâ |
|
|||||||||
¡®«¥¥ ¯®¤à®¡®, ¢ë¤¥«ïï ¢ ¨å, ªà®¬¥ ã¯à ¢«¥¨ï, ¢¥è¨¥ |
|
||||||||||||
¢®§¬ã饨ï '(t), |
â ª¦¥ à §¤¥«ïï ¢ë室®© ᨣ « |
ã¯à - |
|||||||||||
¢«ï¥¬ë© yc(t) ¨ ¨§¬¥àï¥¬ë© ym(t) ¢ë室ë. ®£¤ |
ãà ¢¥¨ï |
||||||||||||
(1.3) ¯à¨¨¬ îâ ¢¨¤ |
|
|
|
|
|
|
|
||||||
x(t) = Ax(t) + Buu(t) + B''(t) yc(t) = Ccx(t) ym(t) = Cmx(t):
¥ª®â®àëå á«ãç ïå ¯®¤®¡ ï ¤¥â «¨§ æ¨ï ®ª §ë¢ ¥âáï 㤮¡- ®© ¨ ¡ã¤¥â ¨á¯®«ì§®¢ âìáï ¨¦¥.
1.3. ¨¥ ਧ æ¨ï ãà ¢¥¨© á®áâ®ï¨ï
а¥ «мле б¨бв¥¬ е ¢б¥£¤ ¯а¨бгвбв¢гов ¥«¨¥©л¥ § - ¢¨б¨¬®бв¨, ®¡гб«®¢«¥л¥, ¯а¨¬¥а, в ª¨¬¨ б¢®©бв¢ ¬¨ д¨- §¨з¥бª¨е §¢¥м¥¢, ª ª блй¥¨¥, «одв, ¥зг¢бв¢¨в¥«м®бвм, ªг«®®¢® ("бге®¥") ва¥¨¥ ¨ в ª ¤ «¥¥. в¨ ндд¥ªвл ¯а¨¢®- ¤пв ª ¥«¨¥©®бв¨ б¨бв¥¬л ¢ ж¥«®¬. ¥в®¤л ¨бб«¥¤®¢ ¨п ¥«¨¥©ле б¨бв¥¬ ¡г¤гв а бᬮва¥л ¢ £« ¢¥ 11. б. 242. б- б«¥¤®¢ ¨¥ б¨бв¥¬л ¬®¦® бгй¥бв¢¥® г¯а®бв¨вм ¯гв¥¬ «¨- ¥ ਧ 樨 ¥¥ ¬®¤¥«¨, â.¥. ¯à¨¡«¨¦¥®© § ¬¥®© ãà ¢¥¨© ¢¨¤ (1.1) ãà ¢¥¨ï¬¨ (1.2) (¨«¨, ¤«ï ¤¨áªà¥âëå ¯à®æ¥áᮢ,
{¨á¯®«ì§®¢ ¨¥¬ (1.5) ¢¬¥áâ® (1.4)).
áᬮâਬ ¯à®æ¥áá «¨¥ ਧ 樨 ¢ ®¡é¥¬ ¢¨¤¥. ãáâì
¤¨ ¬¨ª á¨áâ¥¬ë ®¯¨áë¢ ¥âáï ãà ¢¥¨ï¬¨ á®áâ®ï¨ï (1.1)
x(t) = f(x u t) y(t) = g(x u t): |
(1.6) |
¢¥¤¥¬ ¥ª®â®àë¥ ¯à®¨§¢®«ì® ¨§¬¥ïî騥áï ¯® ¢à¥¬¥- ¨ ("®¯®àë¥") äãªæ¨¨ x (t) 2 Rn ¨ u (t) 2 Rm. ©¤¥¬ «¨- ¥©ãî ç áâì à §«®¦¥¨ï äãªæ¨© f ( ) g( ) ¢ ®ªà¥áâ®á⨠x (t) u (t) ¢ àï¤ ¥©«®à . 6 १ã«ìâ ⥠¯®«ã稬
x(t) + x(t) = f(x (t) u (t) t) + @f(x u t) |
|
x(t) + |
|
|||||
|
@x |
|
|
|
|
|
||
|
|
|
|
|
|
|||
|
+@f (x u t) |
|
|
u(t) + O2 |
(1.7) |
|||
|
@u |
|
|
|
|
|
|
|
6 «ï ®áãé¥á⢨¬®á⨠í⮩ ®¯¥à 樨 âॡã¥âáï ¤¨ää¥à¥æ¨à㥬®áâì |
||||||||
äãªæ¨© f( ) g( ) ¯® x u ¢ ®ªà¥áâ®á⨠x (t) |
u (t). |
|
|
|
|
|||
21 |
|
|
|
|
|
|
|
|
