Файловый архив студентов. Файловый архив студентов.
1284 вуза, 4929 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Уфимский Государственный Авиационный Технический Университет
Предмет:
Теория автоматического управления
Файл:

Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления

.pdf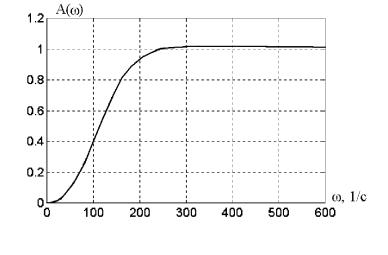
Скачиваний:
130
Добавлен:
02.05.2014
Размер:
2.56 Mб
Скачать
☆

¨á. 1.9. ¬¯«¨â㤭®-ç áâ®â­ ï å à ªâ¥à¨á⨪ ª®«¥¡ - ⥫쭮£® ª®­âãà

¥ªáâ ¯à®£à ¬¬ë ­ ï§ëª¥ MATLAB ¤«ï à áç¥â ª®«¥¡ ⥫쭮£® ª®­âãà

L=4.0v

R=800v

C=10e-6v

 

{ § ¤ ­¨¥ §­ 祭¨© ¯ à ¬¥â஢\

 

T=sqrt(L*C),

xi=R/2*sqrt(C/L), K=L*C

 

{ ¢ëç¨á«¥­¨¥ T K

 

 

ommax=600v

omega=0:ommax/100:ommaxv

 

{ § ¤ ­¨¥ §­ 祭¨© ç áâ®âë !\

 

s=j*omegav

% { ®¯à¥¤¥«¥­¨¥ à£ã¬¥­â s = |!

\

W=K*s.

2 ./(T 2*s. 2+ 2*xi* T*s+ 1)v

 

{ ¯®¤áâ ­®¢ª

s ¢ W(s)\

 

A=abs( W)vb

b

b

 

{ ¢ëç¨á«¥­¨¥ \

 

 

plot(omega, A, 'w'), grid

 

{ ¢ë¢®¤ ­

£à 䨪. à ¬¥âà 'w' § ¤ ¥â 梥⠫¨­¨¨

­ £à 䨪¥ (á¬. [72, 81, 139])

ਬ¥à 2. ¥â ⥫ì­ë© ¯¯ à â. ®«ã稬 ⥯¥àì ¤¨ - £à ¬¬ã ®¤¥ («®£ à¨ä¬¨ç¥áª¨¥ ç áâ®â­ë¥ å à ªâ¥à¨á⨪¨) à áᬮâ७­®£® ¢ëè¥ ¢ ¯à¨¬¥à¥ 2 ­ á. 28 «¥â ⥫쭮£® ¯- ¯ à â (1.16). ¨­¥ ਧ®¢ ­­ ï ¬®¤¥«ì ¯à®¤®«ì­®£® 㣫®- ¢®£® ¤¢¨¦¥­¨ï ¯à¨­ïâ ¢ ¢¨¤¥ (1.33), ᮮ⢥âáâ¢ãî- 騥 ¯¥à¥¤ â®ç­ë¥ ä㭪樨 ¨¬¥îâ ¢¨¤ (1.36). áᬮâਬ

52

«¥£ª¨© á® á«¥¤ãî騬¨ §­ 祭¨ï¬¨ ¯ à ¬¥â஢ ­ ­¥-

ª®â®à®¬ ०¨¬¥ ¯®«¥â [4]: ay =

2:10 [c;1]

ay = 0:16[c;1]

amz = 29:4 [c;2 ]

am!zz = 2:18 [c;1]

;am¢z

= 60:7 [c;2]: 믮«­ïï

¢лз¨б«¥­¨п, ¯®«гз¨¬ б«¥¤гойго ¯¥а¥¤ в®з­го дг­ªж¨о ¯®

㣫ã â ­£ ¦ :

 

 

 

 

 

 

 

¢

 

(60:7s + 127)

 

 

k#( s + 1)

 

W# (s) =

;2

+ 4:28s + 34:0)

=

 

;2 2

 

 

 

s(s

 

s(T s + 2 T s + 1)

 

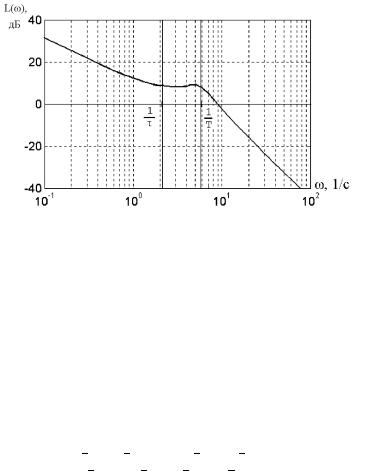
£¤¥ ª®íää¨æ¨¥­â ¯¥à¥¤ ç¨ k# = 3:75 [c;1] ¯®áâ®ï­­ë¥ ¢à¥¬¥­¨= 0:48 [c] T = 0:17 [c] ª®íää¨æ¨¥­â ¤¥¬¯ä¨à®¢ ­¨ï = 0:37 : ¨ £à ¬¬ ®¤¥ ( ) «¥â ⥫쭮£® ¯¯ à â ¯® 㣫ã â ­£ ¦ ¯à¥¤áâ ¢«¥­ ­ à¨á. 1.10

¨á. 1.10. ¨ £à ¬¬ ®¤¥ «¥â ⥫쭮£®

¯¯ à â .

¥ªáâ ¯à®£à ¬¬ë ­ ï§ëª¥ MATLAB ¤«ï à áç¥â

ç áâ®â­ëå

å à ªâ¥à¨á⨪ «¥â ⥫쭮£®

¯¯ à â

 

 

a

 

alpha

 

 

y= -2.10v

a

 

 

delta

 

y= 0.16v

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

alpha

 

 

m= 29.4v

a

 

omega

 

m = 2.18v

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

delta

 

m= 60.7v

 

 

 

 

 

 

 

 

 

 

 

 

 

ãà ¢­¥-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

{ § ¤ ­¨¥ §­ 祭¨© ¯ à ¬¥â஢ a a a

a!z a ¢

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y y

mz

 

mz

mz

 

­¨© (1.33)\

num=- a delta m*[1, - a alpha y]

den=[1, a omega m, -a alpha y, ...

53

a alpha m, -a alpha y*a omega m, 0]

{ ä®à¬¨à®¢ ­¨¥ ¬ áᨢ®¢ ª®íää¨æ¨¥­â®¢ ç¨á«¨â¥«ï ¨ §­ - ¬¥­ â¥«ï ¯¥à¥¤ â®ç­®© ä㭪樨 W ¢ (s) ¨§ (1.34)\

#

k=-n1(2)/d1(3), tau=n1(1)/n1(2) T=sqrt(1/d1(3)), ksi=d1(2)/d1(3)/2/T

{ ¢ëç¨á«¥­¨¥ ¯ à ¬¥â஢ k# T ¯¥à¥¤ â®ç­®© ä㭪樨 W#om=logspace(¢ (s)\ -1, 2)v

{ § ¤ ­¨¥ §­ 祭¨© ç áâ®âë !\

[mag, phase]=bode(num, den, om)v

{ ¢ëç¨á«¥­¨¥ ç áâ®â­ëå å à ªâ¥à¨á⨪ á ¯®¬®éìî ¯à®æ¥- ¤ãàë bode (á¬. ਫ®¦¥­¨¥)

lmag=20*log10(mag)v

{ ¯¥à¥¢®¤ §­ 祭¨© ¢ ¤¥æ¨¡¥«ë\

semilogx(om, lmag, 'w', 1/tau, 0, '+w', 1/T, 0, '+w'), grid

{ ¢ë¢®¤ ¤¨ £à ¬¬ë ®¤¥ ( ) ­ £à 䨪. ¨¬¢®«ë '+' ¢ë¢®¤ïâáï ­ ®á¨ ! ¤«ï 㪠§ ­¨ï ᮯàï£ îé¨å ç áâ®â [15, 76].

«ï ç¨á«¥­­®£® ­ 宦¤¥­¨ï ¯¥à¥¤ â®ç­ëå ä㭪権 ¨ ç - áâ®â­ëå å à ªâ¥à¨á⨪ ­¥¯®á।á⢥­­® ¯® ãà ¢­¥­¨ï¬ á®-

áâ®ï­¨ï á¨áâ¥¬ë ¬®¦­® ¨á¯®«ì§®¢ âì MATLAB-¯à®£à ¬¬ã:

A=[a

 

 

alpha

 

 

 

y, 0 , -a

 

alpha

 

yv...

 

 

 

 

 

 

 

a

 

 

 

alpha

 

m, -a

 

omega

 

m, -a

 

alpha

 

mv...

 

 

 

 

 

 

 

 

0

1

 

 

 

0 ]v

B=[a

 

 

delta

 

yv -a

 

delta

 

mv 0]v C=[0 0 1]v D=0v

 

 

 

 

 

{ä®à¬¨à®¢ ­¨¥ ¬ âà¨æ ãà ¢­¥­¨© á®áâ®ï­¨ï (1.33)

[n, d]=ss2tf(A, B, C, D, 1)v

{¢ëç¨á«¥­¨¥ ¬ áᨢ®¢ ª®íää¨æ¨¥­â®¢ ¬ âà¨ç­®© ¯¥à¥¤ - â®ç­®© ä㭪樨 \

[mag, phase]=bode(A, B, C, D, 1, om)v

{¢ëç¨á«¥­¨¥ ç áâ®â­ëå å à ªâ¥à¨á⨪.

¬¥â¨¬, ç⮠१ã«ìâ âë ¢ëç¨á«¥­¨© ¡ã¤ãâ ­¥áª®«ìª® ®â- «¨ç âìáï ¨§-§ ¢«¨ï­¨ï ¯ à ¬¥âà ay¢ å à ªâ¥à¨§ãî饣® ¯®¤ê¥¬­ãî ᨫã àã«¥© ¢ëá®âë. â®â ¯ à ¬¥âà ­¥ ãç¨âë-

¢ ¥âáï ¢ (1.34) ¤«ï ª®¬¯ ªâ­®á⨠¢ëà ¦¥­¨©, ­® ¢ª«î祭 ¢ ¬ âà¨æã B ¢ ¯à®£à ¬¬¥.

54

ਬ¥à 3. ¬®à⨧¨à®¢ ­­ ï âà ­á¯®àâ­ ï á¨áâ¥-

¬ ©¤¥¬ ç áâ®â­ë¥ å à ªâ¥à¨á⨪¨ âà ­á¯®àâ­®© á¨áâ¥- ¬ë (1.19), á. 32. ® ¯¥à¥¤ â®ç­ë¬ äã­ªæ¨ï¬ W1(s) W2(s)

¯®«ã祭­ë¬ ¢ ¯. 1.5.3. (¯à¨¬¥à 4, á. 38), ¯®«ãç ¥¬ á«¥¤ãî- 騥 ¢ëà ¦¥­¨ï ¤«ï :

 

 

 

 

k1k2

 

 

 

A1(!) = jm1m2!4

; (k1m1 + k1m2 + k2m1)!2 + k1k2j

 

A2(!) =

jm1m2!

4

m1!2jk1 ; m2!2j

2

+ k1k2j

:

 

 

; (k1m1 + k1m2 + k2m1)!

 

 

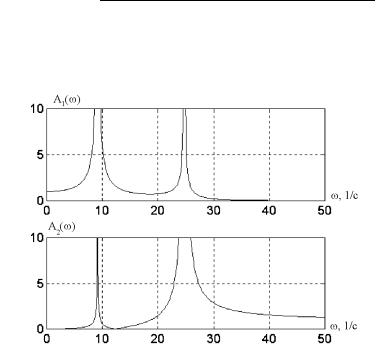
ª ç¥á⢥ ¯à¨¬¥à

­

 

à¨á. 1.11 ¯®ª § ­ë , à ááç¨â ­-

­ë¥ ¯à¨ á«¥¤ãîé¨å §­ 祭¨ïå ¯ à ¬¥â஢ [126]: m1 = 500 [ª£], m2 = 400 [ª£], k1 = 60[ª /¬], k2 = 170[ª /¬].

¨á. 1.11. âà ­á¯®àâ­®© á¨á⥬ë.

¥ªáâ MATLAB-¯à®£à ¬¬ë ¤«ï à áç¥â ç áâ®â­ëå å à ªâ¥à¨á⨪ âà ­á¯®àâ­®© á¨á⥬ë

k

 

1= 60e3 v

k

 

 

2= 170e3 v

 

 

 

m

 

1= 500 v

m

 

2= 400 v

 

 

{ ¢¢®¤ ¯ à ¬¥â஢ á¨á⥬ë\

ommax= 50 v

 

 

omega=0:ommax/500:ommaxv

 

 

 

 

 

55

{ § ¤ ­¨¥ §­ 祭¨© ç áâ®âë

 

!\

 

 

 

 

 

 

 

 

 

 

A

 

 

 

1=k

 

 

 

1*k

 

 

2./abs(m

 

1*m

 

2*omega. 4-...

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(k

 

 

1*m

 

 

1+ k

 

1*m

 

2+k

 

2*m

 

 

 

1).*omega. 2+ k

 

1*k

 

2 )v

 

 

 

 

 

 

 

 

 

 

 

 

A

 

2=m

 

1*omega. 2 .*abs(k

 

1- m

 

2.*omegab

. 2)./...

 

 

 

 

 

 

abs(m

 

1*m

 

2*omega. 4-...

 

 

 

 

 

 

 

 

b

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(k

 

1*m

 

1+ k

 

1*mb

2+k 2*m 1).*omega. 2+ bk 1*k 2)v

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

{ ¢ëç¨á«¥­¨¥ A1 (!b) A2

(!)\

 

 

 

 

 

 

 

subplot(211), plot(omega, A

 

1, 'w'), gridb

 

 

 

 

 

 

 

 

 

 

 

axis([0 ommax 0 10])

 

 

 

 

 

 

2, 'w'), grid

 

 

 

 

 

subplot(212), plot(omega, A

 

 

 

 

 

 

 

 

 

 

 

 

axis([0 ommax 0 10])

 

 

 

 

 

 

 

 

 

 

 

 

 

 

{ ¢ë¢®¤ £à 䨪®¢ . à ¬¥âà axis § ¤ ¥â ¤¨ ¯ §®­ë

ª®®à¤¨­ â­ëå ®á¥©.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

¤ ­­®© ¯à®£à ¬¬¥ ¢ëç¨á«¥­¨ï ¢ë¯®«­¥­ë ¯® ¯à¨¢¥¤¥­-

­ë¬ ¢ëè¥ ­ «¨â¨ç¥áª¨¬ ¢ëà ¦¥­¨ï¬. ­ «®£¨ç­® ¯à¨¬¥àã

2, ¬®¦­® ­¥ ¢ë¯®«­ïâì ­ «¨â¨ç¥áª¨å ¢ëª« ¤®ª, ¯®«ãç âì

ç¨á«¥­­® ¯® ¬ âà¨æ ¬ ãà ¢­¥­¨© á®áâ®ï­¨ï á¨á⥬ë á

¯®¬®éìî ¯à®æ¥¤ãàë bode.

 

 

 

 

ਬ¥à 4. ¨ä஢®© 䨫ìâà. ¯. 1.5.3. á. 45, ¯®«ãç¥-

­

¯¥à¥¤ â®ç­ ï äã­ªæ¨ï ­¥à¥ªãàᨢ­®£® æ¨ä஢®£® 䨫ì-

âà

(1.22), ¨¬¥îé ï ¢¨¤ (1.38) W(z) =

1 + z + z2 + z3

: «ï ­ -

 

 

宦¤¥­¨ï ç áâ®â­ëå å à ªâ¥à¨á⨪ 䨫ìâà

4z4

¢ë¯®«­¨¬ ¯®¤-

áâ ­®¢ªã z = e|!: ®«ã稬 W(e|! ) =

1 + e|! + e2|! + e3|!

:

 

 

 

 

 

4e4|!

à áᬠâਢ ¥¬®¬ á«ãç ¥ ¢¢¨¤ã ᨬ¬¥âਨ ¢ëà ¦¥­¨ï ¤«ï

W(z) ¯à¨ à áç¥â¥ ç áâ®â­ëå å à ªâ¥à¨á⨪ 㤮¡­® ¢ë¯®«- ­¨âì ¯à¥®¡à §®¢ ­¨ï W(e|! ) = 0:25 e;4|! +e;3|! +e;2|! +e;|! =

0:25

 

e;2:5|! e;1:5|! +e;0:5|! +e0:5|! +e1:5|!

 

= 0:5

 

e;2:5|!

 

cos 1:5! +

 

 

 

= e

;2:5|!

 

;

 

 

 

 

 

 

cos 0:5!

 

cos! cos 0:5!: âáî¤

䨫ìâà

A(!)

 

 

|!

 

;

 

 

 

 

 

 

 

;

 

j1W(.12e.

 

j

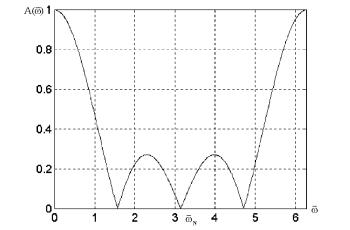
= jcos(!) cos(0:5!)j: à 䨪 A(!) ¯à¥¤áâ ¢«¥­ ­ à¨á.

 

 

¥ªáâ MATLAB-¯à®£à ¬¬ë ¤«ï à áç¥â ç áâ®â­ëå

 

 

 

 

 

 

å à ªâ¥à¨á⨪ æ¨ä஢®£® 䨫ìâà

 

 

 

omega=0:0.005:2*piv

z=exp(i*omega)v

 

 

 

 

{ ®¯à¥¤¥«¥­¨¥ §­ 祭¨©

à£ã¬¥­â

z = e|!

¯¥à¥¤ â®ç­®©

ä㭪樨 ¤«ï ¢ëç¨á«¥­¨ï ç áâ®â­ëå å à ªâ¥à¨á⨪ ¤¨áªà¥â-

­®© á¨á⥬ë\

 

 

W= (1+ z+ z. 2+ z. 3)./z. 4/4v

b

b

b

{ ¢ëç¨á«¥­¨¥ W(e|!)\

 

 

 

 

56
C B

A=abs(W)v

plot(omega, A, 'w'), grid, axis([0, 2*pi, 0, 1])

{ ¢ëç¨á«¥­¨¥ ¨ ¢ë¢®¤ £à 䨪 .

¨á. 1.12.

æ¨ä஢®£® 䨫ìâà

¬ ¥ ç ­ ¨ ¥ .

à áᬮâ७­ëå ¢ëè¥ ¯à¨¬¥à å ç -

áâ®â­ë¥ å à ªâ¥à¨á⨪¨ ®¯à¥¤¥«ï«¨áì ¯®á«¥ ¯à¥¤áâ ¢«¥­¨ï ¯¥à¥¤ â®ç­ëå ä㭪権 ¯® ᮮ⢥âáâ¢ãî騬 ¢å®¤ ¬ ¨ ¢ëå®-

¤ ¬ ¢ ¢¨¤¥ ®â­®è¥­¨ï ¬­®£®ç«¥­®¢. ¢ëç¨á«¨â¥«ì­®¬ ®â- ­®è¥­¨¨ ®ª §ë¢ ¥âáï ¯à¥¤¯®çâ¨â¥«ì­ë¬ ¯®«ì§®¢ âìáï ­¥¯®- á।á⢥­­® ¯®¤áâ ­®¢ª®© = |! («¨¡® = e|! { ¤«ï ¤¨áªà¥â-

­ëå á¨á⥬) ¢ ¢ëà ¦¥­¨¥ ¤«ï १®«ì¢¥­âë R( ) =

 

In ;A ;1:

в¥¬ ¨б¯®«м§говбп б®®в­®и¥­¨п R( + |) =

 

(

+ |)In

 

;1

 

;

 

 

 

 

;

 

 

 

 

 

;1

 

 

;

;

A

 

=

 

A

 

|In

( In

 

A)2

+ 2In

 

= U + |V £¤¥

 

In

;

;

 

;

 

 

 

 

 

 

 

 

= |!

 

 

 

 

;

 

 

 

= Re = Im

(¯à¨

¯®¤бв ¢«повбп §­ з¥­¨п = 0

= !

¯à¨ = e|! §­ 祭¨ï = cos! = sin!). १ã«ì-

â ⥠ç¨á«¥­­® ­ 室ïâáï ¬ âà¨ç­ë¥ §­ 祭¨ï ¢¥é¥á⢥­­®© ¨ ¬­¨¬®© ç áâ®â­ëå å à ªâ¥à¨á⨪ U V: ¬­®¦ ï ¨å ­ ¬ âà¨æë ¯®«ãç ¥¬ ¢¥é¥á⢥­­ãî ¨ ¬­¨¬ãî ç áâ®â­ë¥

å à ªâ¥à¨á⨪¨ ¯® § ¤ ­­®¬ã ¢å®¤ã ¨ ¢ë室ã. ª®© ᯮ- ᮡ ¯®§¢®«ï¥â ¨§¡¥¦ âì ¢ëç¨á«¥­¨ï ¯¥à¥¤ â®ç­ëå ä㭪権 ®â ¯ à ¬¥âà ¨, ªà®¬¥ ⮣®, ¨á¯®«ì§®¢ âì íä䥪⨢­ë¥ ¢ë- ç¨á«¨â¥«ì­ë¥ «£®à¨â¬ë ¬ âà¨ç­®© «£¥¡àë.

57

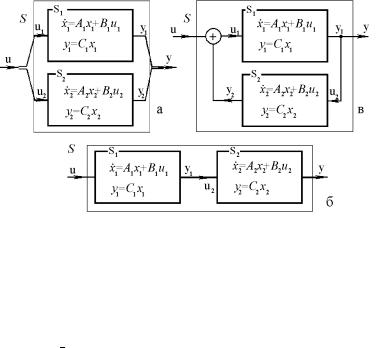
1.7. à ¢­¥­¨ï á®áâ®ï­¨ï ¯à¨ ᮥ¤¨­¥­¨¨ á¨á⥬

® ¬­®£¨å á«ãç ïå ¢®§­¨ª ¥â ­¥®¡å®¤¨¬®áâì ¯®«ãç¨âì ¥¤¨- ­ë¥ ãà ¢­¥­¨ï ¤«ï á¨á⥬ë, á®áâ®ï饩 ¨§ ­¥áª®«ìª¨å ᮥ¤¨-

­¥­­ëå ¬¥¦¤ã ᮡ®© ¯®¤á¨á⥬. ª¨¥ á¨áâ¥¬ë ¨­®£¤ ­ §ë- ¢ îâáï "ª®¬¯®§¨â­ë¬¨". áᬮâਬ, ª ª ¢ë£«ï¤¨â à¥è¥- ­¨¥ í⮩ § ¤ ç¨ ¯à¨ ®¯¨á ­¨¨ ¬®¤¥«¥© á¨á⥬ ãà ¢­¥­¨ï¬¨ á®áâ®ï­¨ï [47].

1.7.1. ¥§ ¢¨á¨¬ë¥ ¯®¤á¨á⥬ë

áᬮâਬ ¢­ ç «¥ ­ ¨¡®«¥¥ ¯à®á⮩ á«ãç ©, ª®£¤ ª®¬¯®- §¨â­ ï á¨á⥬ á®á⮨⠨§ ¤¢ãå ­¥§ ¢¨á¨¬ëå ¯®¤á¨á⥬ (à¨á. 1.13, ). 室®¬ á¨á⥬ë ï¥âáï ¢¥ªâ®à, ¯®«ã祭­ë© ®¡ê-

¥¤¨­¥­¨¥¬ ¢å®¤®¢ ª ¦¤®© ¯®¤á¨á⥬ë, ¢ë室®¬ { ®¡ê¥¤¨- ­¥­¨¥ ¨å ¢ë室®¢.

¨á. 1.13. âàãªâãàë ª®¬¯®§¨â­ëå á¨á⥬.

ãáâì á¨á⥬ë Si i = 1 2 ®¯¨áë¢ îâáï ãà ¢­¥­¨ï¬¨ á®- áâ®ï­¨ï

xi(t) = Ai(t)xi (t) + Bi(t)ui(t) yi(t) = Ci (t)xi(t)

¢ ª®â®àëå ¬ âà¨æë Ai(t) Bi(t) Ci(t) ¨¬¥îâ à §¬¥àë, ᮮ⢥â- á⢥­­®, ni ni ni mi li mi : ¢¥¤¥¬ ᮢ®ªã¯­ë¥ (®¡é¨¥) ¢¥ª-

 

 

x1

(t) x2(t)

2Rn1+n2 ¢å®¤

 

â®àë: á®áâ®ï­¨ï x(t) = col

u(t) =

 

 

 

 

 

 

 

 

58

 

 

col

u1

(t) u2

(t)

 

 

m1

+m2

¨ ¢ë室

 

y1(t) y2

(t)

 

R

l1

+l2

:

 

 

2 R

 

 

 

 

ã¡¥¦¤ ¥¬áï,

2

 

 

 

¡ê¥¤¨­¨¢

ãà ¢­¥­¨ï á¨áâ¥¬ë ¢ ®¤­®,

 

çâ® ®â­®á¨â¥«ì­® ¢¢¥¤¥­­ëå ¯¥à¥¬¥­­ëå íâ® ãà ¢­¥­¨¥ ¨¬¥- ¥â ¢¨¤ (1.3)

x(t) = A(t)x(t) + B(t)u(t) y(t) = C(t)x(t)

¢ ª®â®à®¬ ¬ âà¨æë A(t) B(t) C(t) ¨¬¥ов б«¥¤гойго ¡«®з- ­го бвагªвгаг:

A1(t)

0n1 n2

B(t) =

B1 (t)

A(t) = 0n2 n1

A2(t)

0n2 m1

 

 

C1 (t)

0l1 n2

:

 

C(t) = 0l2 n1

C2(t)

1.7.2. ®á«¥¤®¢ ⥫쭮¥ ᮥ¤¨­¥­¨¥

0n1 m2

B2 (t)

ãáâì ⥯¥àì ¢å®¤®¬ á¨á⥬ë S ï¥âáï ¢å®¤ ¯®¤á¨á⥬ë S1

u(t) u1(t)\ ¢ë室 á¨áâ¥¬ë ®¡à §ã¥âáï ¢ë室®¬ ¯®¤á¨á⥬ë

S2 y(t)

y2(t) ¨ ¢ë室 ¯¥à¢®© ¯®¤á¨á⥬ë S1 ¯®áâ㯠¥â ­

¢å®¤ ¯®¤á¨á⥬ë S2

â ª, çâ® ¨å à §¬¥à­®á⨠ᮢ¯ ¤ îâ, l1 =

m2 ¨ u2

(t) = y1(t): ¥à¥¯¨è¥¬ ãà ¢­¥­¨ï ¯®¤á¨á⥬ á ãç¥â®¬

㪠§ ­­®© á¢ï§¨ ¬¥¦¤ã ­¨¬¨ (à¨á. 1.13, ¡). ®«ã稬

x1

(t) = A1(t)x1

(t) + B1

(t)u(t)

y1(t) = C1 (t)x1(t)

x2

(t) = A2(t)x2

(t) + B2

(t)C1(t)x1 (t) y(t) = C2 (t)x2(t)

®âªã¤

¯®«ãç ¥¬ ¬ âà¨æë ãà ¢­¥­¨© ¢ ä®à¬¥ (1.3) ¢¨¤

 

 

A1(t)

0n1 n2

B1(t)

 

 

A(t) = B2(t)C1 (t) A2(t)

B(t) = 0n1 m2

 

 

 

C(t) = [ 0l2 n1

C2(t) ] :

1.7.3.

®¥¤¨­¥­¨¥ á ®¡à â­®© á¢ï§ìî

ãáâì ⥯¥àì ¯®¤á¨á⥬ë ᮥ¤¨­¥­ë á ®¡à â­®© á¢ï§ìî, â.¥.

¢ë室 ¯®¤á¨á⥬ë S2

á㬬¨àã¥âáï (¨«¨ ¢ëç¨â ¥âáï) á® ¢å®-

¤®¬ ¢á¥© á¨á⥬ë S

¨ ¯®áâ㯠¥â ­ ¢å®¤ ¯®¤á¨á⥬ë S1:

ª ç¥á⢥ ¢ë室

á¨á⥬ë S ¨á¯®«ì§ã¥¬ ¢ë室 ¯®¤á¨á⥬ë S2

(à¨á. 1.13, ¢).

ª¨¬ ®¡à §®¬, ¬ë áç¨â ¥¬, çâ® m1 = l2

m2 = l1 m = m1 l = l2 n = n1 + n2 u1(t) = u(t) y2 (t)

59

u2(t) = y1(t): ãç¥â®¬ á¢ï§¨ ¬¥¦¤ã ¯®¤á¨á⥬ ¬¨ ¨å ãà ¢­¥- ­¨ï ¯à¨­¨¬ îâ ¢¨¤

x1(t)=A1(t)x1(t) B1 (t)C2(t)x2 (t)+B1 (t)u(t) y(t)=C1(t)x1 (t) x2(t)=A2(t)x2(t)+B2 (t)C1(t)x1 (t)

¨ ¬ ва¨жл ¢ (1.3) ®¯а¥¤¥«повбп ¢ла ¦¥­¨п¬¨

A1

(t)

 

B1 (t)C2

(t)

B1 (t)

 

A(t) = B2(t)C1(t)

 

A2(t)

 

B(t) = 0n1 m2

 

C(t) = [C1(t)

0l1 n2 ] :

 

­ «®£¨ç­ë¬ ®¡à §®¬ ¬®£ãâ ¡ëâì ¯®«ã祭ë ãà ¢­¥­¨ï á®- áâ®ï­¨ï ¯à¨ ¯®á«¥¤®¢ ⥫쭮¬ ᮥ¤¨­¥­¨¨, â ª¦¥ ¢ ¤à㣨å, ¡®«¥¥ á«®¦­ëå á«ãç ïå. ⬥⨬, çâ® å®âï ¨§«®¦¥­¨¥ íâ®- £® ¯ à £à ä ª á «®áì ­¥¯à¥à뢭ëå á¨á⥬, ¢á¥ ¯®«ã祭­ë¥

¢ëè¥ á®®â­®è¥­¨ï á¯à ¢¥¤«¨¢ë (¯®á«¥ ®ç¥¢¨¤­ëå ¨§¬¥­¥­¨© ¢ ®¡®§­ 祭¨ïå) ¨ ¤«ï ¤¨áªà¥â­ëå á¨á⥬.

1.8. ८¡à §®¢ ­¨¥ ¡ §¨á

ª ®â¬¥ç¥­® ¢ ¯. 1.1. á. 15, ¢¥ªâ®à á®áâ®ï­¨ï ¬®¦¥â ¡ëâì ¯à¥¤áâ ¢«¥­ ­¥¥¤¨­á⢥­­ë¬ ®¡à §®¬ { ¯à®¨§¢®«ì­®¥ ¢§ ¨¬­®- ®¤­®§­ ç­®¥ ®â®¡à ¦¥­¨¥ ¯à®áâà ­á⢠á®áâ®ï­¨© X ¢ á¥- ¡ï ¤ ¥â ­®¢ë© ¢¥ªâ®à, ª®â®àë© â ª¦¥ ¬®¦­® ¨á¯®«ì§®¢ âì

¢ ª ç¥á⢥ á®áâ®ï­¨ï á¨á⥬ë. â®â ¢¥ªâ®à ¨¬¥¥â ¤à㣨¥ §­ 祭¨ï ª®¬¯®­¥­â. ᮡ¥­­® à á¯à®áâà ­¥­® «¨­¥©­®¥ ­¥- ¢ë஦¤¥­­®¥ ¯à¥®¡à §®¢ ­¨¥ á ª¢ ¤à â­®© n n-¬ âà¨æ¥© T det T 6= 0: ਠ⠪®¬ ¯à¥®¡à §®¢ ­¨¨ £®¢®àïâ, çâ® ¢¥ªâ®à á®áâ®ï­¨ï ¯à¥¤áâ ¢«¥­ ¢ ­®¢®¬ ¡ §¨á¥, ᮮ⢥âáâ¢ãî饥 ¯à¥®¡à §®¢ ­¨¥ ãà ¢­¥­¨© ­ §ë¢ î⠯८¡à §®¢ ­¨¥¬ ¡ §¨á

ãà ¢­¥­¨© á®áâ®ï­¨ï. ¨¤ ãà ¢­¥­¨© á¨áâ¥¬ë ¯à¨ í⮬ ¨§¬¥- ­ï¥âáï, ­® ®áâ îâáï ­¥¨§¬¥­­ë¬¨ ¢å®¤®-¢ë室­ë¥ ᮮ⭮è¥- ­¨ï. ç áâ­®áâ¨, ¤«ï áâ 樮­ à­ëå «¨­¥©­ëå á¨á⥬ ®áâ - ¥âáï ­¥¨§¬¥­­®© ¯¥à¥¤ â®ç­ ï äã­ªæ¨ï. áᬮâਬ ¯à¥- ®¡à §®¢ ­¨¥ ¡ §¨á ¡®«¥¥ ¯®¤à®¡­®.

ãáâì T { ­¥¢ë஦¤¥­­ ï ¬ âà¨æ ¯®à浪 n det T 6= 0 x(t)2Rn { ¢¥ªâ®à á®áâ®ï­¨ï á¨á⥬ë. ¯à¥¤¥«¨¬ ¢¥ªâ®à

x~(t) = T x(t): ᨫ㠭¥¢ë஦¤¥­­®á⨠¬ âà¨æë ¯à¥®¡à §®¢ - ­¨ï T ¢¥ªâ®à x~(t) ®¯à¥¤¥«ï¥âáï ¯® x(t) ¢§ ¨¬­®-®¤­®§­ ç­® ¨

60

¬®¦­® § ¯¨á âì x(t) = T ;1x~(t): 17 ¥à¥¯¨è¥¬ ãà ¢­¥­¨ï á®- áâ®ï­¨ï (1.2) ¢ ¯à¥®¡à §®¢ ­­®¬ ¢¨¤¥. ç¨âë¢ ï çâ® x(t) = T ;1x~(t) ¯®«ã稬

x~(t) = T A(t)T;1x~(t) + T B(t)u(t) x~(t0) = x~0 = T x0

(1.43)

y(t) = C(t)T;1x~(t) + D(t)u(t)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

~

 

;1

 

~

 

~

 

¡®§­ 稬 ¬ âà¨æë A(t) = T A(t)T

 

B

(t) =

T B(t) C

(t) =

C(t)T ;1: âáî¤

¯®«ãç ¥¬ ãà ¢­¥­¨ï (1.43) ¢ ä®à¬¥ (1.2):

x~(t)

=

~

 

~

 

x~(t0) = x~0

= T x0

 

A(t)~(x t) + B(t)u(t)

 

(1.44)

y(t)

=

~

(t)~(x t) + D(t)u(t):

 

 

 

 

 

C

 

 

 

 

 

 

à ¢­¥­¨ï (1.44) ¯à¥¤áâ ¢«ïîâ ᮡ®© ãà ¢­¥­¨ï á®áâ®ï­¨ï

á¨á⥬ë (1.2) ¢ ­®¢®¬ ¡ §¨á¥. 祢¨¤­®, çâ® à §«¨ç­ëå ä®à¬ ãà ¢­¥­¨© á®áâ®ï­¨ï ¬®¦¥â ¡ëâì § ¯¨á ­® ­¥®£à ­¨ç¥­­® ¬­®£®. 18

áᬮâਬ ⥯¥àì áâ 樮­ à­ë¥ ॠ«¨§ã¥¬ë¥ á¨á⥬ë,

§¤ ­­ë¥ ãà ¢­¥­¨ï¬¨

x(t) = Ax(t) + Bu(t)

y(t) = Cx(t) + Du(t):

(1.45)

१ã«ìâ ⥠¯à¥®¡à §®¢ ­¨ï á ¬ âà¨æ¥© T ¯®«ã稬

 

~

~

~

(1.46)

x~(t) = Ax~(t) + Bu(t)

y(t) = Cx~(t) + Du(t)

~ ~ ~

®¯à¥¤¥«¥­ë ¢ëè¥. ëç¨á«¨¬ ¯¥à¥¤ -

£¤¥ ¬ âà¨æë A B C

â®ç­ãî äã­ªæ¨î á¨á⥬ë (1.46) ¯® ä®à¬ã«¥ (1.25) ¨ ¢ë¯®«­¨¬

¯à¥®¡à §®¢ ­¨ï: 19

 

 

 

 

 

 

 

 

 

;

 

 

;

 

 

 

 

 

~

 

 

;

;

 

 

 

 

 

 

 

;1

 

 

 

 

 

 

 

 

 

~

 

 

~ ;1

~

 

 

 

 

;1

 

sIn

 

T AT

;1

 

;1

T B + D =

W(s) = C sIn

A B + D = CT

 

 

 

 

 

 

 

 

 

 

 

= C

;

sIn ; A

 

 

T

+ D

W(s):

 

 

 

 

ª¨¬ ®¡à §®¬, ¯¥à¥¤ â®ç­ ï äã­ªæ¨ï á¨áâ¥¬ë ¯®á«¥ ¯à¥-

®¡à §®¢ ­¨ï ¯®¤®¡¨ï

 

 

á ¬ âà¨æ¥© T ­¥ ¨§¬¥­¨« áì. ®¢®àïâ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

17 «¨â¥à âãॠ¨­®£¤

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

¨á¯®«ì§ãî⠯८¡à §®¢ ­¨¥ x~(t) = T ;1x(t): à¨

â ª®¬ ¯à¥®¡à §®¢ ­¨¨ ¢ ¯®á«¥¤ãîé¨å ä®à¬ã« å ­ ¤® ¢¬¥áâ® ¬ âà¨æë T

¨á¯®«ì§®¢ âì T ;1 (¨ ­ ®¡®à®â).

 

 

 

 

 

 

 

 

 

 

 

 

 

18 ¤¥áì ­¥ à áᬮâ७® ¯à¥®¡à §®¢ ­¨¥ á ¯¥à¥¬¥­­®© ¢® ¢à¥¬¥­¨ ¬ -

âà¨æ¥© T

= T (t). âà¨æ

 

 

~

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A(t) ¯à¨ â ª®¬ ¯à¥®¡à §®¢ ­¨ï ¯à¨­¨¬ ¥â ¢¨¤

~

_

(t) + T(t)A(t) T

;1

(t):

 

 

 

 

 

 

 

 

 

 

 

 

 

A(t) =

T

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

19 ᯮ«ì§®¢;

­ë ⮦¤

¥á⢠(AB);1 = B;1A;1

det(AB) = det A det B

á¯à ¢¥¤«¨¢ë¥ ¤«ï ª¢ ¤à â­ëå ­¥¢ë஦¤¥­­ëå ¬ âà¨æ.

61

Соседние файлы в предмете Теория автоматического управления
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности