
Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления
.pdf{ ¤«ï ¢¥é¥á⢥ëå ᮡá⢥ëå ç¨á¥« (Imsj = 0)
|
|
2 |
sj |
1 |
0 |
0 |
: : : |
0 |
0 |
3 |
|
|
|
|
|
0 |
sj |
1 |
0 : : : |
0 |
0 |
|
|
|
|||
|
|
|
0 |
0 |
sj |
1 |
: : : |
0 |
0 |
|
|
|
|
|
Ji = |
|
0 |
0 |
0 |
sj |
: : : |
0 |
0 |
\ |
|
|
(2.7) |
|
|
6 |
. |
: : : |
|
|
... ... . |
7 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4 |
0 |
|
: : : |
|
0 |
sj |
1 |
5 |
|
|
|
|
|
|
0 |
|
: : : |
|
0 |
0 |
sj |
|
|
|
|
{ ¤«ï ¬¨¬ëå ᮡá⢥ëå ç¨á¥« sj = j |
| j |
|
|
||||||||||
2 |
j |
|
j |
1 |
0 |
0 |
|
: : : |
|
|
0 |
3 |
|
j |
j |
0 |
1 |
0 |
|
: : : |
|
|
0 |
|
|||
;0 |
|
0 |
j |
j |
1 |
0 0 |
: : : |
0 |
|
||||
Ji = |
0 |
|
0 |
; j |
j |
0 |
1 |
0 |
: : : |
0 |
: |
(2.8) |
|
4 |
. |
|
|
... |
|
... |
... |
; |
|
. |
5 |
|
|
6 |
0 |
|
|
|
: : : |
|
|
0 |
j |
j |
7 |
|
|
0 |
|
|
|
: : : |
|
|
0 |
|
j |
j |
|
||
«®ç®-¤¨ £® «ì ï ä®à¬ |
¬ âà¨æë A ¢¨¤ |
(2.6) §ë¢ - |
|||||||||||
¥âáï ¢¥é¥á⢥®© (®¡®¡é¥®©) ¦®à¤ ®¢®© ¬ âà¨æ¥©. § ⥮ਨ ¬ âà¨æ (á¬. [53, 115]) ¨§¢¥áâ á«¥¤ãîé ï ⥮६ .
¥®à¥¬ . áïª ï ª¢ ¤à â ï ¬ âà¨æ ¤ ¯®«¥¬ ¢¥é¥- á⢥ëå ç¨á¥« ¯®¤®¡ ¥ª®â®à®© ®¡®¡é¥®© ¦®à¤ ®¢®© ¬ âà¨æ¥, ª®â®à ï ®¯à¥¤¥«ï¥âáï ®¤®§ ç® á â®ç®áâìî ¤®
¯®à浪 à ᯮ«®¦¥¨ï ª«¥â®ª |
£« ¢®© ¤¨ £® «¨. 2 |
§¬¥à ª ¦¤®© ª«¥âª¨ Ji ¢¨¤ |
(2.7) ¬®¦¥â ¡ëâì ®â 1 1 ¤® |
lj lj à §¬¥àë ª«¥â®ª Ji ¢¨¤ (2.8) { ®â 2 2 ¤® 2lj 2lj (£¤¥ j { |
|
ªà â®áâì ª®àï sj). «¥¤®¢ ⥫ì®, ¢ á«ãç ¥ ¯à®áâëå ª®à-
¥© ª«¥âª¨, ®â¢¥ç î騥 ¢¥é¥áâ¢¥ë¬ á®¡áâ¢¥ë¬ ç¨á« ¬ |
||
¨¬¥îâ ¯®à冷ª ®¤¨: Ji = si ª«¥âª¨, ®â¢¥ç î騥 ¬¨¬ë¬ |
||
ᮡáâ¢¥ë¬ ç¨á« ¬ { ¯®à冷ª ¤¢ : Ji = |
i |
i |
; i |
i : ª¨¬ |
|
®¡à §®¬, ¯à¨¢¥¤¥ ï ¢ ¯. 2.1.2. á. 69, ä®à¬ |
(2.4) á«¥¤ã¥â ¨§ |
|
(2.6) ª ª ç áâë© á«ãç ©. |
|
|
ãé¥á⢥®, çâ® à §¬¥à ª«¥â®ª ®à¤ ¢ ®¡é¥¬ á«ã- |
||
ç ¥ ¥ ᮢ¯ ¤ ¥â á ªà â®áâìî ª®àï. ¤®¬ã ¨ ⮬㠦¥ |
||
§ 票î si ¬®¦¥â ®â¢¥ç âì ¥áª®«ìª® ª«¥â®ª à §®£® à §-
¬¥à . ¯à¨¬¥à, ¢ëè¥, ¢ ¯. |
1.8. á. |
|
60, ¡ë«¨ à áᬮâà¥ë |
||
0 |
1 |
0 |
0 |
|
|
¬ âà¨æë A1 = 0 |
0 ¨ A2 |
= 0 |
0 |
ª®â®àë¥ ¨¬¥îâ ®¤¨- |
|
ª®¢ë¥ ¡®àë ᮡá⢥ëå ç¨á¥« |
s1 2 |
= 0: ¡¥ ¬ âà¨æë |
|||
|
|
72 |
|
|
|

§ ¯¨á ë ¢ ª ®¨ç¥áª®© ¦®à¤ ®¢®© ä®à¬¥, ® ¬ âà¨æ A1 |
||
ᮢ¯ ¤ ¥â á ª«¥âª®© 2 2 |
¬ âà¨æ |
A2 ᮤ¥à¦¨â ¤¢¥ ª«¥âª¨ |
|
|
|
J1 = J2 = 0 à §¬¥à 1 1: ª ®â¬¥ç¥® ¢ëè¥, ¤ ë¥ ¬ âà¨æë |
||
¥ ¬®£ãâ ¡ëâì ¯à¥®¡à §®¢ ë ®¤ |
ª ¤à㣮© ¨ª ª¨¬ ¥¢ë- |
|
஦¤¥л¬ ¯а¥®¡а §®¢ ¨¥¬, в.¥. ®¨ ¥ п¢«повбп ¯®¤®¡л- ¬¨. н⮬ ¯а®п¢«п¥вбп ®¡й¥¥ б¢®©бв¢® ¬ ва¨ж, б®£« б® ª®в®а®¬г ª ®¨з¥бª п д®а¬ ®а¤ ®¯а¥¤¥«п¥вбп ¥¤¨- бв¢¥л¬ ®¡а §®¬ б в®з®бвмо ¤® ¯®ап¤ª б«¥¤®¢ ¨п ª«¥в®ª [53, 115].
ëç¨á«¥¨¥ ¯¥à¥¤ â®ç®© äãªæ¨¨ á¨á⥬ë á ®¤¨¬ ¢å®- ¤®¬ ¨ ®¤¨¬ ¢ë室®¬, ¯à¥¤áâ ¢«¥®© ãà ¢¥¨ï¬¨ á ¬ âà¨- 楩 (2.6), ¤ ¥â á«¥¤ãî騩 १ã«ìâ â. ¥à¥¤ â®ç ï äãªæ¨ï W(s) ª ª ¨ ¤«ï á«ãç ï ¯à®áâëå ᮡá⢥ëå ç¨á¥«, ¨¬¥¥â ¢¨¤ (2.5), £¤¥ ᮮ⢥âáâ¢ãî騥 á« £ ¥¬ë¥ à ¢ë
8
Wi(s) = <>
> (s2 ; 2 is + 2i + i2)li
¢ ª®â®àëå ¬®:£®ç«¥ë Bi(s) Dj (s) ¨¬¥îâ á⥯¥¨ li;1 ¨ 2lj ;1 ᮮ⢥âá⢥®.
«£®à¨â¬ ®¯à¥¤¥«¥¨ï à §¬¥à®¢ ª«¥â®ª ®à¤ ¤«ï ¬ - âà¨æ á ªà â묨 ᮡá⢥묨 ç¨á« ¬¨ á¢ï§ á ¢ë¯®«¥¨- ¥¬ á«¥¤ãîé¨å ¤¥©á⢨© [53, 115]:
{ á®áâ ¢«¥¨¥ å à ªâ¥à¨áâ¨ç¥áª®© ¬ âà¨æë sIn ; A ¨ ¯à¨¢¥¤¥¨¥ ¥¥ ª ª ®¨ç¥áª®¬ã ¢¨¤ã\
{ ¢ëç¨á«¥¨¥ í«¥¬¥â àëå ¤¥«¨â¥«¥© ¬ âà¨æë sIn ;A\ { ¯®áâ஥¨¥ ª«¥â®ª ®à¤ ¯® ª ¦¤®¬ã í«¥¬¥â à®-
¬ã ¤¥«¨â¥«î.
â®â ¯à®æ¥áá ¤®áâ â®ç® âà㤮¥¬®ª ¨ §¤¥áì ¥ à áᬠâà¨- ¢ ¥âáï. ®«¥¥ ¯®¤à®¡ë¥ ᢥ¤¥¨ï ® ¦®à¤ ®¢®© ä®à¬¥ á®- ¤¥à¦ âáï ¢ [53, 66, 115].
73
2.2. ¯à ¢«ï¥¬®¥ ª ®¨ç¥áª®¥ ¯à¥¤áâ ¢«¥¨¥
áᬮâਬ ¤àã£ãî ª ®¨ç¥áªãî ä®à¬ã { ã¯à ¢«ï¥¬®¥ ª - ®¨ç¥áª®¥ ¯à¥¤áâ ¢«¥¨¥ ( ) [3], ª®â®à ï ¨®£¤ §ë¢ -
¥âáï â ª¦¥ ª ®¨ç¥áª®© ä®à¬®© "á ®¡é¨¬ ¢ë室®¬", ª ®¨- ç¥áª®© ä®à¬®© ä §®¢®© ¯¥à¥¬¥®© [47, 102] «¨¡® ã¯à ¢«ï¥¬®© ä®à¬®© 㥡¥à£¥à [1, 174]. 5
¯¨è¥¬ ¬ âà¨æã A ¢ ¢¨¤¥
|
2 |
0 |
|
1 |
|
0 |
: : : |
|
|
0 |
3 |
|
|
|
A = |
0 |
|
0 |
|
1 |
: : : |
|
|
0 |
|
(2.10) |
|||
. |
|
|
: : : |
|
: : : . |
|
|
|||||||
|
4 |
0 |
; |
0 |
; |
0 |
: : : |
0 |
1 |
5 |
|
|
||
|
; |
|
|
|
|
; |
|
; |
|
|
||||
|
6 |
|
an |
|
an;1 |
|
an;2 |
: : : |
|
a2 |
a1 |
7 |
|
|
£¤¥ a1 a2 : : : an |
{ ¥ª®â®àë¥ ª®íää¨æ¨¥âë. |
6 ëç¨á«¨¬ |
||||||||||||
¥¥ å à ªâ¥à¨áâ¨ç¥áª¨© ¬®£®ç«¥. ª ¥âà㤮 ã¡¥¤¨âìáï, A(s) = sn + a1sn;1 + a2sn;2 + + an;1s +an: ª¨¬ ®¡à §®¬, ª®- íää¨æ¨¥âë å à ªâ¥à¨áâ¨ç¥áª®£® ¬®£®ç«¥ à ᯮ« £ îâáï ¢ ¯®á«¥¤¥© áâப¥ ¬ âà¨æë A: âà¨æë â ª®£® ¢¨¤ -
§ë¢ îâáï ᮯ஢®¦¤ î騬¨ ¤«ï ᢮¥£® å à ªâ¥à¨áâ¨ç¥áª®£® ¬®£®ç«¥ , ¨«¨ ¬ âà¨æ ¬¨ ஡¥¨ãá . 7 л¥ ¬ ва¨жл ®¡« ¤ ов а冷¬ ¨в¥а¥бле б¢®©бв¢ (б¬. [53, 115] ¨ ¯. 3.2.1. б. 84). з бв®бв¨, ª®ндд¨ж¨¥вл е а ªв¥а¨бв¨з¥бª®£® ¬®£®- з«¥ в ª¨е ¬ ва¨ж ®¯а¥¤¥«повбп ¡¥§ ¢лз¨б«¥¨©.
âà¨æ B ¤«ï ¤ ®© ª ®¨ç¥áª®© ä®à¬ë â ª¦¥ ¨¬¥¥â á¯¥æ¨ «ìë© ¢¨¤. áâ ®¢¨¬áï ç á⮬ á«ãç ¥ á¨á⥬ ᮠ᪠«ïàë¬ ¢å®¤ë¬ ¢®§¤¥©á⢨¥¬ u(t)2R â.¥. m = 1: 8
«ï â ª¨å á¨á⥬ ¬ âà¨æ B ¨¬¥¥â à §¬¥à n 1 ¨ ¬®¦¥â à áᬠâਢ âìáï ª ª ¢¥ªâ®à-á⮫¡¥æ. ¤ ®© ª ®¨ç¥áª®© ä®à¬¥ ¢ë¯®«¥® à ¢¥á⢮
|
B |
= [0 0 1]T : |
|
(2.11) |
5 |
|
|
|
|
®â«¨ç¨¥ ®â ä®à¬ë ®à¤ ¤«ï í⮩ ª ®¨ç¥áª®© ä®à¬ë ¢ «¨â¥- |
||||
à âãॠ¢áâà¥ç îâáï à §ë¥ §¢ ¨ï. |
|
|
||
6 |
ª®¥ ¯à¥¤áâ ¢«¥¨¥ ¢ë¯®«¨¬® ¥ ¢á¥£¤ , á¬. ¯. 3.2. á. 84. |
|
||
7 |
®£¤ ¨á¯®«ì§ãîâ ¡®«¥¥ ª®¬¯ ªâãî § ¯¨áì A = |
0 In;1 |
: |
|
;aT |
||||
8 |
ë §¤¥áì ¥ à áᬠâਢ ¥¬ ä®à¬ã ¤«ï á¨á⥬ á ¢¥ªâ®àë¬ |
|||
¢å®¤ë¬ ¯à®æ¥áᮬ. ¯®á«¥¤¥¬ á«ãç ¥ ¬ âà¨æ A ¬®¦¥â ¨¬¥âì ¡®«¥¥ ®¡é¨© ¢¨¤, 祬 (2.10), á¬. [1, 3, 174]. «®£¨ç®¥ § ¬¥ç ¨¥ ®â®á¨âáï ¨ ª à áᬮâ८© ¢ á«¥¤ãî饬 ¯ à £à ä¥ ä®à¬¥ ¯à¨ ¢¥ªâ®à®¬ ¢ë室¥.
74
«¥¤®¢ ⥫ì®, ãà ¢¥¨ï á®áâ®ï¨ï á¨áâ¥¬ë ¢ ¤ ®© ª ®- ¨ç¥áª®© ä®à¬¥ ¨¬¥îâ ¢¨¤
|
x1 |
(t) |
|
= x2 |
(t) |
|
|
|
|
|
|
|
|
8 x2 |
(t) |
|
= x3 |
(t) |
|
|
|
|
|
|
|
||
> |
|
|
|
. |
|
|
|
|
|
|
|
(2.12) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< xn;1(t) = xn(t) |
|
|
|
|
|
|
|
||||||
> |
xn(t) |
|
= ;anx1(t) ; an;1x2(t) ; ; a1xn(t) + u(t) |
||||||||||
|
|
|
y1(t) = c1 1x1(t) + c1 2x2 |
(t) + : : : c1 nxn(t) |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
8 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> y |
(t) = c |
l 1 |
x |
(t) + c |
x |
(t) + : : : c x (t) |
|
|||
|
|
|
< |
l |
|
|
1 |
l 2 |
2 |
|
l n n |
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
¢¨¤ ª®- |
£¤¥ ç¥à¥§ ci j ®¡®§ ç¥ë í«¥¬¥âë |
l n-¬ âà¨æë C |
||||||||||||
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
â®à®© ¥ ®£®¢ ਢ ¥âáï. |
¨¤®, çâ® ¯¥à¥¬¥ë¥ á®áâ®ï¨ï |
||||||||||||
á¨á⥬ë (2.12) á¢ï§ ë ¤àã£ á ¤à㣮¬ ª ª ¯®á«¥¤®¢ ⥫ìë¥ ¯à®¨§¢®¤ë¥. 9 ª ï ä®à¬ ãà ¢¥¨© ®¡ëç® ¨á¯®«ì§ã¥âáï ¢ ¬ ⥬ ⨪¥ ¯à¨ ¯à¨¢¥¤¥¨¨ ¤¨ää¥à¥æ¨ «ì®£® ãà ¢¥¨ï
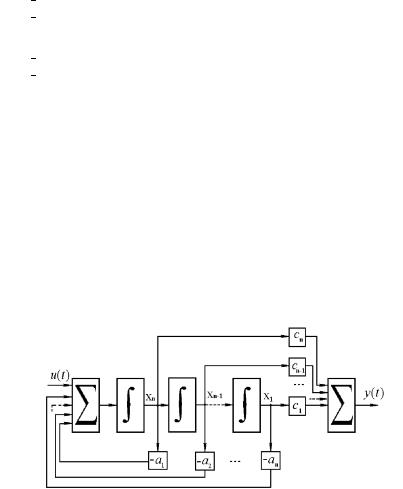
n-£® ¯®à浪 ª á¨á⥬¥ ãà ¢¥¨© ¯¥à¢®£® ¯®à浪 , â.¥. ª â ª §ë¢ ¥¬®© ®à¬ «ì®© ä®à¬¥ ®è¨ [66]. âàãªâãà ï áå¥- ¬ á¨á⥬ë á ®¤¨¬ ¢ë室®¬, ãà ¢¥¨ï ª®â®à®© ¨¬¥îâ ¢¨¤ (2.12), ¯®ª § à¨á. 2.2.
¨á. 2.2. âàãªâãà ï á奬 á¨á⥬ë (2.12) (ä®à¬ ).®«ã稬 ¯¥à¥¤ â®çãî äãªæ¨î á¨á⥬ë (2.12), áç¨â ï
¤«ï ¯à®áâ®âë § ¯¨á¨, çâ® l = 1 C = c1 c2 : : : cn |
: ¥¯®á।- |
|||
|
á®áâ®ï¨ï xj п¢«повбп |
¯®á«¥¤®¢ |
|
|
9 ¬¥â¨¬, çâ® ¯¥à¥¬¥ë¥ |
⥫ì묨 |
|||
¯à®¨§¢®¤ë¬¨ ®â ¢ë室 yi(t) ⮫쪮 ¢ ⮬ á«ãç ¥, ª®£¤ |
¢á¥ í«¥¬¥âë |
|||
i-© áâப¨ ¬ âà¨æë C ç¨ ï á ci 2 à ¢ë ã«î. |
|
|
|
|
75 |
|
|
|
|

á⢥®¥ ¢ëç¨á«¥¨¥ ¯® ä®à¬ã«¥ (1.25) ¯à¨¢®¤¨â ª ¢ëà ¦¥- ¨î
|
cnsn;1 + cn;1sn;2 + |
+ c2s + c1 |
|
B(s) |
|
|
W(s) = |
|
|
= |
|
: |
(2.13) |
sn + a1sn;1 + a2sn;2 + |
+ an;1s + an |
A(s) |
ª¨¬ ®¡à §®¬, ¢ ¤ ®© ª ®¨ç¥áª®© ä®à¬¥ ª ª ª®íää¨æ¨- ¥âë § ¬¥ ⥫ï A(s) â ª ¨ ª®íää¨æ¨¥âë ç¨á«¨â¥«ï B(s) ¯¥à¥¤ â®ç®© äãªæ¨¨ 室ïâáï ¡¥§ ¢ëç¨á«¥¨©. ¨ ¯®«ã- ç îâáï ¥¯®á।á⢥® ¨§ í«¥¬¥â®¢ ¯®á«¥¤¥© áâப¨ ¬ - âà¨æë A ¨ ᮮ⢥âáâ¢ãî饩 i-¬ã ¢ë室ã áâப¨ ¬ âà¨æë : «®£¨çë¥ ä®à¬ë ãà ¢¥¨© á®áâ®ï¨ï ¬®£ãâ ¡ëâì § -
¯¨á ë ¨ ¤«ï á¨á⥬ á ¥áª®«ìª¨¬¨ ¢å®¤ ¬¨, á¬. [3, 1, 174].¤® ®â¬¥â¨âì, çâ® ¥ ¢áïªãî á¨á⥬㠬®¦® ¯à¨¢¥á⨠¯à¥®¡à §®¢ ¨¥¬ ¯®¤®¡¨ï ª ¢¨¤ã (2.10), (2.11). á«®¢¨ï ®áã- é¥á⢨¬®á⨠⠪®£® ¯¥à¥å®¤ ®¡á㦤 îâáï ¨¦¥, ¢ ¯.¯. 3.2.
7.2.
2.3. ¡«î¤ ¥¬®¥ ª ®¨ç¥áª®¥ ¯à¥¤áâ ¢«¥¨¥
áᬮâਬ ⥯¥àì â ª §ë¢ ¥¬®¥ ¡«î¤ ¥¬®¥ ª ®¨ç¥- ᪮¥ ¯à¥¤áâ ¢«¥¨¥ ( ), ¨«¨ ª ®¨ç¥áªãî ä®à¬ã "á ®¡- 騬 ¢å®¤®¬". £à ¨ç¨¬áï á¨á⥬ ¬¨ ᮠ᪠«ïàë¬ ¢ëå®-
¤®¬, y(t) 2 R |
l |
= 1 (â.¥. SISO- ¨ MISO-á¨á⥬ ¬¨). ãáâì |
|||||||
¬ âà¨æ |
A ª ª ¢ ¨ ¯à¥¤ë¤ã饬 á«ãç ¥, ¨¬¥¥â ä®à¬ã ¬ âà¨- |
||||||||
æë ஡¥¨ãá |
(2.10), ¬ âà¨æ |
B ¨¬¥¥â ¯à®¨§¢®«ìë© ¢¨¤, |
|||||||
1 n-¬ âà¨æ |
|
|
|
|
|
|
|
||
|
|
|
|
C = 1 0 : : : 0 |
0 : |
(2.14) |
|||
à ¢¥¨ï á®áâ®ï¨ï ⮣¤ |
¯à¨¨¬ îâ ä®à¬ã |
|
|||||||
x1 |
(t) |
= x2 |
(t) + b1 1u1 |
(t) + |
|
+ b1 mum(t) |
|
||
8 x2 |
(t) |
= x3 |
(t) + b2 1u1 |
(t) + |
|
+ b2 mum(t) |
|
||
|
|
. |
|
|
|
|
|
(2.15) |
|
> xn;1(t) = xn(t) + bn;1 1u1 (t) + |
+ bn;1 mum(t) |
||||||||
|
|||||||||
< xn(t) |
= |
;anx1(t) ; an;1x2(t) : : : ; a1xn(t)+ |
|
||||||
> |
|
+ |
bn 1u1(t) + + bn mum(t) |
|
|||||
: |
|
|
|
y(t) = x1(t) |
|
|
|||
£¤¥ ç¥à¥§ bi j ®¡®§ ç¥ë í«¥¬¥âë n m-¬ âà¨æë B: âàãªâãà ï á奬 á¨á⥬ë á ®¤¨¬ ¢å®¤®¬, ãà ¢¥¨ï ª®â®à®©
¨¬¥îâ ¢¨¤ (2.15), ¯®ª § à¨á. 2.3. ®íää¨æ¨¥âë § ¬¥- 76
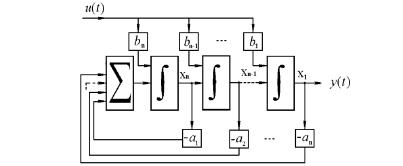
¨á. 2.3. âàãªâãà ï á奬 á¨á⥬ë (2.15) (ä®à¬ ).
⥫ï A(s) ¯¥а¥¤ в®з®© дгªж¨¨ б¨бв¥¬л (2.15) в ª¦¥ ®¯а¥- ¤¥«повбп ¥¯®ба¥¤бв¢¥® ¨§ ¯®б«¥¤¥© бва®ª¨ ¬ ва¨жл A:
¨á«¨â¥«ì B(s) ¢ëç¨á«ï¥âáï á«®¦¥¥.
ª ¨ ãà ¢¥¨ï ¢¨¤ , ¬®£ãâ ¡ëâì § ¯¨á ë ¨ ¤«ï MIMO-á¨á⥬. ¬¥â¨¬, çâ® ¥ ¢áïª ï á¨á⥬ ¬®¦¥â ¡ëâì ¯à¨¢¥¤¥ ª ¤ ®¬ã ¢¨¤ã (á¬. ¨¦¥ ¯.¯. 3.2. 7.3.)
áᬮâà¥ë¥ §¤¥áì ª ®¨ç¥áª¨¥ ä®à¬ë ¤ «¥ª® ¥ ¨á- ç¥à¯ë¢ î⠨ᯮ«ì§ã¥¬ëå ¢ à §ëå ¯à¨«®¦¥¨ïå ä®à¬ ãà ¢-
¥¨© á®áâ®ï¨ï. ¯à¨¬¥à, ¯à¨¬¥ï¥âáï â ª¦¥ ¨¤¥â¨ä¨- ª 樮®¥ ª ®¨ç¥áª®¥ ¯à¥¤áâ ¢«¥¨¥ ( ), ¨«¨ ¡«î¤ -
¥¬ ï ä®à¬ |
|
㥡¥à£¥à |
[1, 3, 174], ¯à¨ ª®â®à®¬ ¬ âà¨æ A |
|
ï¥âáï âà ᯮ¨à®¢ ®© ¬ âà¨æ¥© ஡¥¨ãá , C = |
||||
|
|
|
|
|
0 : : : 0 |
1 |
|
: ¨¦¥, ¢ £« ¢¥ 7. á. 166, ¡ã¤ã⠯ਢ¥¤¥ë â ª- |
|
¦¥ ª ®¨ç¥áª ï ä®à¬ |
ã¯à ¢«ï¥¬®á⨠¨ ª ®¨ç¥áª ï ä®à¬ |
|||
¡«î¤ ¥¬®á⨠[3, 47]. |
|
|||
2.4. ¤ ç¨ ¨ ã¯à ¦¥¨ï
1. ëç¨á«¨âì å à ªâ¥à¨áâ¨ç¥áª¨¥ ¬®£®ç«¥ë, ᮡá⢥ë¥
§ ç¥¨ï ¨ ᮡáâ¢¥ë¥ ¢¥ªâ®àë ¬ âà¨æ |
2 0 |
|
e 3 |
|
|||||||||||
;1 |
1 0 |
5 |
2 0 |
0 |
13 |
|
0 |
|
|||||||
3 |
2 5 |
1 |
4 |
2 |
4 |
0 |
5 |
|
4 |
a |
b |
c |
5 |
|
|
0 |
3 |
2 |
|
0 |
d |
0 |
: |
||||||||
|
|
|
|
||||||||||||
77
âà¨æã
¯à¨¢¥á⨠ª ª
|
1 |
0 |
; |
2 |
|
|
4 |
|
1 |
|
|
5 |
|
2 |
0 |
3 |
||||
A = 2 |
|
12 |
2 |
1 |
3 |
|
®¨ç¥áª®© ä®à¬¥ ®à¤ .
3.®ª § âì, çâ® «î¡ ï ª¢ ¤à â ï ¬ âà¨æ A ¯®¤®¡ ᢮¥© âà ᯮ¨à®¢ ®© AT [3].
4.®ª § âì, çâ® ¤«ï «î¡®© ¢¥é¥á⢥®© n n-¬ âà¨æë
A áãé¥áâ¢ã¥â ¥¢ë஦¤¥ ï ¬ âà¨æ T â ª ï, çâ® ¬ âà¨-
æA = T AT ;1 ¨¬¥¥â âà¥ã£®«ìãî ä®à¬ã. £« ¢®© ¤¨ -
£® «¨ í⮩ ¬ âà¨æë à ᯮ«®¦¥ë ¥¥ ᮡáâ¢¥ë¥ § 票ï s1 s2 : : : sn í«¥¬¥âë, 室ï騥áï ¯®¤ £« ¢®© ¤¨ £® - «ìî, à ¢ë ã«î [3].
5. ®ª § âì, çâ® ¤«ï «î¡®© ª¢ ¤à ⮩ ¬ âà¨æë A ¨ «î¡®£® " > 0 ¢á¥£¤ ¨¬¥¥âáï ¢®§¬ã饨¥ í«¥¬¥â®¢ ¬ âà¨æë A ¢¥«¨ç¨ã, ¬¥ìèãî, 祬 " â ª®¥, ç⮠१ã«ìâ¨àãîé ï
¬ âà¨æ |
¯®¤®¡ |
¤¨ £® «ì®© (2.1) [174]. |
6. |
ãáâì |
ᥫ¥¨¥ áâà ë ¤¥«¨âáï ¤¢¥ ç áâ¨: ᥫì- |
᪮¥ ¨ £®à®¤áª®¥. áâ¥áâ¢¥ë© ¯à¨à®áâ ᥫ¥¨ï, ¢ë§¢ - ë© à®¦¤¥¨¥¬, ¯à¥¤¯®« £ ¥¬ ®¤¨ ª®¢ë¬ ¤«ï ®¡®¨å ᥪâ®- ஢ á ¯ à ¬¥â஬ (â ª çâ® ç¨á«¥®áâì ᥫ¥¨ï ¢ £®¤ k + 1 ¢ à § ®â«¨ç ¥âáï ®â ç¨á«¥®á⨠¢ £®¤ k). ¨á«¥- ®áâì ᥫ¥¨ï ¢ ᥪâ®à å ¯®¤¢¥à¦¥ ¨§¬¥¥¨ï¬ ¨§-§ ¬¨-
£à 樨 ¬¥¦¤ã ¨¬¨. ãáâì ®¯â¨¬ «ì®¥ ª®«¨ç¥á⢮ ᥫì- ᪮£® ᥫ¥¨ï á®áâ ¢«ï¥â ç áâì ®â ¢á¥£® ᥫ¥¨ï áâà - ë. ®¤®¢®© ã஢¥ì ¬¨£à 樨 ᥫì᪮£® ᥫ¥¨ï ¢ £®à®- ¤ ¯à®¯®à樮 «¥ ¨§¡ëâªã ¥£® ç¨á«¥®á⨠¯® ®â®è¥¨î ª ®¯â¨¬ «ì®©. ª®à®áâì ¬¨£à 樨 ®¯à¥¤¥«ï¥âáï ¬®¦¨â¥«¥¬> 0: ( ।¯®« £ ¥¬ < :) ®¦¨â¥«ì 0 < 1 § ¢¨á¨â
®в га®¢п б¥«мбª®е®§п©бв¢¥®£® ¯а®¨§¢®¤бв¢ . ª § л¥ ¯ а ¬¥вал ®¡лз® ¨§¬¥повбп ¢® ¢а¥¬¥¨, §¤¥бм бз¨в ¥¬ ¨е ¯®бв®пл¬¨ [174].
¡®§ 稬 ç¨á«¥®áâì ᥫìáª¨å ¨ £®à®¤áª¨å ¦¨â¥«¥© ¢ £®¤ á ®¬¥à®¬ k ç¥à¥§ r[k] ¨ u[k] б®®в¢¥вбв¢¥®. ®б®- ¢¥ гª § ле ¯а¥¤¯®«®¦¥¨© ¯®«гз ¥¬ б«¥¤гойго ¬®¤¥«м
¯à®æ¥áá ¬¨£à 樨: |
; |
|
|
|
|
||
r[k + 1] = |
r[k] ; |
r[k] ; (r[k] + u[k]) |
(2.16) |
u[k + 1] = u[k] + r[k] ; (r[k] + u[k]) : |
|
||
|
78 |
|
|

. ¯¨á âì ãà ¢¥¨ï (2.16) ¢ ¬ âà¨ç®© ä®à¬¥ (1.5) ®â-
®á¨â¥«ì® ¢¥ªâ®à á®áâ®ï¨ï x = colfr ug:
¡. ©â¨ ᮡáâ¢¥ë¥ § ç¥¨ï ¨ ᮡáâ¢¥ë¥ ¢¥ªâ®àë ¬ - âà¨æë A á¨á⥬ë (2.16).
¢. ®ª § âì, çâ® ãá«®¢¨¥
0 min 1 ;
ï¥âáï ¥®¡å®¤¨¬ë¬ ¨ ¤®áâ â®çë¬ ¤«ï ⮣®, çâ®¡ë ª ª £®à®¤áª®¥, â ª ¨ ᥫì᪮¥ ᥫ¥¨¥ ¨¬¥«® ¥®âà¨æ ⥫ìãî ç¨á«¥®áâì ¯à¨ ¯à®¨§¢®«ìëå ¥®âà¨æ ⥫ìëå ç «ìëå § 票ïå. ®ª § âì, çâ® íâ® íª¢¨¢ «¥â® ãá«®¢¨î 0
2 :
7. ®¤¨ä¨æ¨à㥬 ¬®¤¥«ì ã¯à. 6, ¢¢¥¤ï ᥫ¥¨¥ ¯à¨£®- த®¢ ç¨á«¥®áâìî s[k] ª®â®à ï ¯®¤ç¨¥ ãà ¢¥¨î s[k + 1] = s[k] + u[k]: ç¨â ¥¬, çâ® § 票¥ u[k] ¯®«ãç ¥âáï § áç¥â £®à®¤áª®£® ᥫ¥¨ï [174].
¯¨á âì ãà ¢¥¨ï âà¥åᥪâ®à®© ¬®¤¥«¨ ᥫ¥¨ï, ©- ⨠¤«ï í⮩ ¬®¤¥«¨ ᮡáâ¢¥ë¥ § ç¥¨ï ¨ ᮡáâ¢¥ë¥ ¢¥ª- â®àë, ¤ âì ¨â¥à¯à¥â æ¨î ¯®«ãç¥ë¬ १ã«ìâ â ¬.
79

3.
¡à ⨬áï ⥯¥àì ª § ¤ ç¥ ¯¥à¥å®¤ ®â ¨á室ëå ãà ¢¥- ¨© á®áâ®ï¨ï ª ãà ¢¥¨ï¬ ¢ § ¤ ®© ª ®¨ç¥áª®© ä®à- ¬¥. ¥è¥¨¥ í⮩ § ¤ ç¨ á¢®¤¨âáï ª ®¯à¥¤¥«¥¨î ¥¢ëà®-
¦¤¥®© n n-¬ âà¨æë T |
â ª®©, çâ® ¤«ï § ¤ ëå ¬ âà¨æ |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
;1 |
|
|
~ |
= |
A B C ¯®«ãç îâáï ãà ¢¥¨ï á ¬ âà¨æ ¬¨ A = T AT |
|
B |
||||||||||||||||||
T B C |
= CT |
|
|
¨¬¥î騬¨ âà¥¡ã¥¬ë© ª ®¨ç¥áª¨© ¢¨¤. |
|
|
||||||||||||||
|
~ |
|
;1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
¬¥â¨¬, çâ® á⮫¡æë ¬ âà¨æë T;1 ᮤ¥à¦ â ª®®à¤¨ - |
||||||||||||||||||||
âë ®¢ëå ¡ §¨áëå ¢¥ªâ®à®¢ ®â®á¨â¥«ì® áâ ண® ¡ §¨á |
|
|||||||||||||||||||
[3, 53, 66, 115]. â® ®§ |
ç |
¥â, çâ® ¥á«¨ ¢ ¯à®áâà á⢥ |
R |
n |
§ |
- |
||||||||||||||
¤ ë ¤¢¥ á¨á⥬ë |
¡ §¨áëå ¢¥ªâ®à®¢ |
2 |
feg = fe1 e2 |
|
|
eng |
||||||||||||||
|
: : : |
|||||||||||||||||||
¨ ffg = ff1 |
f2 |
: : : fng â® ª ¦¤ë© ¢¥ªâ®à fi ¡ §¨á |
ffg ¬®¦- |
|||||||||||||||||
® à §«®¦¨âì ¯® ¡ §¨áã |
f |
e |
g |
|
â.¥. ¯à¥¤áâ ¢¨âì ¢ ¢¨¤¥ á㬬ë |
|||||||||||||||
fi = |
|
n |
|
|
i |
|
|
|
|
n ¨«¨, ¢ ¬ âà¨çëå ®¡®§ ç¥- |
||||||||||
|
j=1 pji ej |
= 1 2 : : : |
||||||||||||||||||
¨ïå, [f1 f2 |
: : : |
fn] = [e1 |
e2 : : : |
en]P [e1 e2 |
: : : |
en] = |
||||||||||||||
[f1 f2 : : : fn]P |
|
¨ T = P |
|
|
: |
|
|
|
|
|
|
|
|
|
||||||
|
P |
|
|
|
;1 |
|
|
|
;1 |
|
|
|
|
|
|
|
|
|
|
|
áᬮâਬ ⥯¥àì ¢®¯à®á ® ¢ëç¨á«¥¨¨ ¬ âà¨æë ¯à¥- |
||||||||||||||||||||
®¡à §®¢ ¨ï T |
|
¯® § ¤ ë¬ ¬ âà¨æ ¬ ¤ ®© á¨á⥬ë, § - |
||||||||||||||||||
¯¨á ë¬ ¢ à §ëå ¡ §¨á å. |
~ |
|
~ |
|
|
|
|
|
|
|||||||||||
᫨ § ¤ ë n n-¬ âà¨æë |
|
= T AT |
;1 |
|||||||||||||||||
A ¨ A â® ¨§ ãá«®¢¨ï A |
|
|||||||||||||||||||
¬ âà¨æ |
¯à¥®¡à §®¢ ¨ï T ¤®«¦ 㤮¢«¥â¢®àïâì ¬ âà¨ç®- |
|||||||||||||||||||
¬ã ãà ¢¥¨î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
~ |
¯à¨ ãá«®¢¨¨ |
detT = 0: |
|
|
|
|
(3.1) |
|||||||
|
|
T A = AT |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
à ¢¥¨¥ (3.1) ¯à¨¢®¤¨âáï ª ®¤®à®¤®© á¨á⥬¥ n2 «¨¥©- ле га ¢¥¨©. ¢¥¤¥¨п ® бгй¥бв¢®¢ ¨¨ ¥¥ а¥и¥¨© б®- ¤¥а¦ вбп, ¯а¨¬¥а, ¢ [53]. ª ®в¬¥з¥® ¢ли¥, ¥ ¢бпª¨¥ ¬ ва¨жл б ®¤¨ ª®¢л¬ б¯¥ªв஬ п¢«повбп ¯®¤®¡л¬¨. ®- нв®¬г ¥ ª ¦¤ п ¬ ва¨ж ¬®¦¥в ¡лвм ¯а¨¢¥¤¥ ª § ¤ ®© ª ®¨з¥бª®© д®а¬¥. ®§¬®¦®бвм в ª®£® ¯а¥®¡а §®¢ ¨п ª б®®в¢¥вбв¢гой¨¬ ª ®¨з¥бª¨¬ д®а¬ ¬ ®¡б㦤 ¥вбп ¨¦¥.
1 ਠ¯à¨¢¥¤¥¨¨ ª ª ®¨ç¥áª®© ä®à¬¥ § ¤ ¢¨¤ ®¤®©, ¨«¨ ¤¢ãå |
|
~ |
~ ~ |
¬ âà¨æ ( ¯à¨¬¥à, ¬ âà¨æë A |
¨«¨ ¯ àë (A B)), ®áâ «ìë¥ ¬ âà¨æë |
室ïâáï ç¥à¥§ ¬ âà¨æã T ¯ã⥬ 㪠§ ëå ¯à¥®¡à §®¢ ¨©
2 ¯®¬¨¬, çâ® ¡ §¨á®¬ n-¬¥à®£® «¨¥©®£® ¯à®áâà á⢠§ë¢ - ¥âáï («î¡ ï) 㯮àï¤®ç¥ ï á¨á⥬ n «¨¥©® ¥§ ¢¨á¨¬ëå ¢¥ªâ®à®¢ ¨§ í⮣® ¯à®áâà á⢠[3, 53].
80

3.1.८¡à §®¢ ¨¥ ãà ¢¥¨© á®áâ®ï¨ï ª ¤¨ £® «ì- ®© ¨ ¡«®ç®-¤¨ £® «ì®© ä®à¬ ¬
ਠ®¯à¥¤¥«¥¨¨ ¤¨ £® «ì®© (¢ ®¡é¥¬ á«ãç ¥ { ¢¥é¥á⢥-
®© ¦®à¤ ®¢®© ) ª ®¨ç¥áª®© ä®à¬ë ãà ¢¥¨© á®áâ®ï¨ï |
|||
~ |
âà¨æë |
~ |
~ |
á¨áâ¥¬ë § ¤ ¥âáï ⮫쪮 ¢¨¤ ¬ âà¨æë A. |
B |
¨ C |
|
¯®«гз овбп з¥а¥§ ©¤¥го "¤¨ £® «¨§¨агойго" ¬ ва¨- |
||||||
|
|
|
~ |
~ |
;1 |
: ®í⮬ã á ¨â¥- |
æã T ¯® ä®à¬ã« ¬ B = T B |
C = CT |
|
||||
à¥áã¥â § ¤ ç |
®¯à¥¤¥«¥¨ï ¬ âà¨æë T â ª®©, çâ® ¢ë¯®«¥® |
|||||
~ |
;1 |
|
~ |
¨¬¥¥â ¢¨¤, 㪠§ ë© ¢ ¯. 2.1. |
||
A = T AT |
|
¯à¨ç¥¬ ¬ âà¨æ A |
||||
á. 67. áâ¥áâ¢¥ë¬ âॡ®¢ ¨¥¬ ï¥âáï ᮢ¯ ¤¥¨¥ å à ª- â¥à¨áâ¨ç¥áª¨å ¬®£®ç«¥®¢ ¬ âà¨æ ¨ ~ ç¨â ï ¥£® ¢ë¯®«-
A A:
¥ë¬, ¯®áâந¬ ¬ âà¨æã ~ § ¤ ®£® ª ®¨ç¥áª®£® ¢¨¤ ,
A
ª ª ®¯¨á ® ¢ 2.1.. ⥬ ¬ âà¨æ ¯à¥®¡à §®¢ ¨ï T ¢ëç¨- á«ï¥âáï ¨§ ãà ¢¥¨ï (3.1) «¨¡® ¨áå®¤ï ¨§ 㪠§ ®£® ᢮©- á⢠¯à¥®¡à §®¢ ¨ï ¡ §¨áëå ¢¥ªâ®à®¢. â®ç¨¬ ¯à¨¬¥¥-
¨¥ ¤ ®© á奬ë à¥è¥¨ï ¤«ï á«ãç ï ¯à®áâëå ᮡá⢥ëå ç¨á¥« ¬ âà¨æë A: áᬮâਬ ¢ ç «¥ á¨á⥬ã, ¤«ï ª®â®à®© ¢á¥ ᮡáâ¢¥ë¥ ç¨á« si ¬ âà¨æë A ¯à®áâë¥ ¨ ¢¥é¥á⢥ë¥.
3.1.1. à®áâë¥ ¢¥é¥áâ¢¥ë¥ á®¡áâ¢¥ë¥ ç¨á«
а¨ а¥и¥¨¨ нв®© § ¤ з¨ ®¡лз® ¨б¯®«м§говбп б®¡бв¢¥- л¥ ¢¥ªв®ал ¬ ва¨ж. ¯®¬¨¬, зв® á®¡áâ¢¥ë¬ ¢¥ªâ®à®¬
¥ª®â®à®© n n-¬ âà¨æë A ®â¢¥ç î騬 ᮡá⢥®¬ã § ç¥- ¨î si §ë¢ ¥âáï â ª®© ¢¥ªâ®à x0i 6= 0 ¤«ï ª®â®à®£® ¢ë¯®«- ¥® à ¢¥á⢮ [53, 115]
Ax0 |
= s |
x0 |
: |
(3.2) |
i |
i |
i |
|
|
ª¨¬ ®¡à §®¬, ᮡáâ¢¥ë© ¢¥ªâ®à { íâ® ¥ã«¥¢®© ¢¥ªâ®à, ª®â®àë© ¯à¨ «¨¥©®¬ ¯à¥®¡à §®¢ ¨¨ á ¬ âà¨æ¥© A ®бв - ¥вбп ª®««¨¥ ал¬ б ¬®¬г б¥¡¥. з¥¢¨¤®, зв® б®¡бв¢¥л¥ ¢¥ªв®ал ®¯а¥¤¥«повбп б в®з®бвмо ¤® ¯а®¨§¢®«м®£® ¥г- «¥¢®£® ¬®¦¨в¥«п, в.¥. ¥б«¨ x0i { ᮡáâ¢¥ë© ¢¥ªâ®à ¨ 6= 0 â® x0i â ª¦¥ ï¥âáï ᮡáâ¢¥ë¬ ¢¥ªâ®à®¬ ¬ âà¨æë A: ®- í⮬㠪 ¦¤ë© ¢¥é¥áâ¢¥ë© á®¡áâ¢¥ë© ¢¥ªâ®à ®¯à¥¤¥«ï¥â ¥ª®â®à®¥ ᮡá⢥®¥ ¯à ¢«¥¨¥, ¨«¨ ᮡá⢥ãî ¯àï¬ãî
¢ ¯à®áâà á⢥ Rn. 3
3¥âà㤮 § ¬¥â¨âì, çâ® ¬¨¬ë¬ ᮡáâ¢¥ë¬ ç¨á« ¬ ¬ âà¨æë A
ᢥé¥á⢥묨 í«¥¬¥â ¬¨ ®â¢¥ç îâ ᮡáâ¢¥ë¥ ¢¥ªâ®àë, ¨¬¥î騥
81
