Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления

á¨á⥬, á ®¤­®© áâ®à®­ë, ¨ ¬¥â®¤ ¬¨ ç¨á«¥­­®£® à¥è¥­¨ï § - ¤ ç¨ ®è¨ { á ¤à㣮© [3, 72]. ¥ ¢¤ ¢ ïáì ¢ ¯®¤à®¡­®áâ¨, à áᬮâਬ ­¥ª®â®àë¥ å à ªâ¥à­ë¥ ®á®¡¥­­®á⨠¯®á«¥¤­¥© § ¤ ç¨. ãáâì âॡã¥âáï ¯à®¨­â¥£à¨à®¢ âì ãà ¢­¥­¨¥

£® ç¨á«¥­­®¥ à¥è¥­¨¥ ¬®¦¥â ¡ëâì ¯®«ã祭® ¢ ¢¨¤¥ ­¥ª®â®-

ண® ४ãà७⭮£® ᮮ⭮襭¨ï xk+1 = '(xk k) £¤¥

k = 0 1 2 : : : { ­®¬¥à è £ (¨â¥à 樨), §­ 祭¨ï xk ᮮ⢥â- áâ¢ãîâ §­ 祭¨ï¬ ¨áª®¬®© ä㭪樨 x(t) ¢ ¤¨áªà¥â­ë¥ ¬®¬¥­- âë ¢à¥¬¥­¨ tk = kh £¤¥ h > 0 { è £ ¨­â¥£à¨à®¢ ­¨ï. 14 ¨¤ ä㭪樨 '(xk k) ®¯à¥¤¥«ï¥âáï ¯® ¨á室­®© ä㭪樨 f (x t) á®- £« á­® ¢ë¡à ­­®¬ã ¬¥â®¤ã ç¨á«¥­­®£® ¨­â¥£à¨à®¢ ­¨ï. - ¯à¨¬¥à, ¨á¯®«ì§ãï ¬¥â®¤ ©«¥à , ¯®«ãç ¥¬ ¨§¢¥áâ­ãî ä®à- ¬ã«ã

¬¥â¨¬, çâ® (6.59) á â®ç­®áâìî ¤® ®¡®§­ 祭¨© ᮢ¯ ¤ ¥â á ãà ¢­¥­¨¥¬ (6.14), ¢ ª®â®à®¬ ¬ âà¨æë P Q ¯®«ãç¥­ë ­ ®á­®- ¢¥ ¯à¨¡«¨¦¥­­®© ä®à¬ã«ë (6.20) ¤«ï ¬ âà¨ç­®© íªá¯®­¥­âë.á⮩稢®áâì ¯®«ã祭­®© ç¨á«¥­­®© ¯à®æ¥¤ãàë ®¯à¥¤¥«ï¥â- áï ¯à¨¢¥¤¥­­ë¬¨ ¢ëè¥ ¢ ¯. 6.10.1. ᢮©á⢠¬¨ ¤ ­­®© ¯- ¯à®ªá¨¬ 樨: ¤«ï A ¨ T0 = h ¤®«¦­® ¢л¯®«­пвмбп ­¥а ¢¥­-

á⢮ (6.53). 15 «¥¤®¢ ⥫쭮, ¥á«¨ ᮡá⢥­­ë¥ ç¨á« á¨áâ¥- ¬ë ¢¥«¨ª¨ ¯® ¬®¤ã«î (ç⮠ᮮ⢥âáâ¢ã¥â ¬ «ë¬ ¯®áâ®ï­­ë¬

14¤¥áì ¬ë ­¥áª®«ìª® ®â®è«¨ ®â ¯à¨­ïâëå ¢ëè¥ ®¡®§­ 祭¨© ¤«ï ¤¨áªà¥â­ëå ¯à®æ¥áᮢ.

15ਢ¥¤¥­­ë¥ §¤¥áì ¤«ï «¨­¥©­ëå á¨á⥬ १ã«ìâ âë ¬®¦­® à á¯à®-

áâà ­¨âì ¨ ­ § ¤ çã ¨­â¥£à¨à®¢ ­¨ï ­¥«¨­¥©­®£® ãà ¢­¥­¨ï (6.56), ¥á«¨

162

¢à¥¬¥­¨), çâ®¡ë ¯®«ãç¨âì ãá⮩稢®¥ à¥è¥­¨¥, á«¥¤ã¥â ¢ë- ¡¨à âì è £ ¨­â¥£à¨à®¢ ­¨ï h ¤®áâ â®ç­® ¬ «ë¬. â® ¯à¨- ¢®¤¨â ª §­ ç¨â¥«ì­ë¬ § âà â ¬ ¬ 設­®£® ¢à¥¬¥­¨. ஬¥ ⮣®, á«¥¤ã¥â ãç¥áâì, ç⮠㬥­ì襭¨¥ ¢¥«¨ç¨­ë h ¢ë§ë¢ ¥â 㢥«¨ç¥­¨¥ ¨­áâà㬥­â «ì­ëå ®è¨¡®ª, á¢ï§ ­­ëå á ª®­¥ç­®- áâìî à §à來®© á¥âª¨ . ®¤®¡­ë¬ ᢮©á⢮¬ ®¡« ¤ î⠢ᥠ⠪ ­ §ë¢ ¥¬ë¥ ï¢­ë¥ ¬¥в®¤л з¨б«¥­­®£® ¨­в¥£а¨а®¢ - ­¨п, ª®в®ал¥ ¤«п «¨­¥©­ле бв ж¨®­ а­ле б¨бв¥¬ б¢®¤пвбп ª ¯¯а®ªб¨¬ ж¨п¬ ¥©«®а (6.19). ¨¡®«¥¥ ®вз¥в«¨¢® ­¥- ¤®бв вª¨ п¢­ле ¬¥в®¤®¢ ¯а®п¢«повбп ¯а¨ а¥и¥­¨¨ ¦¥á⪨å á¨á⥬, ã ª®â®àëå ᮡá⢥­­ë¥ ç¨á« ®â«¨ç îâáï ¯® ¬®¤ã- «î ¢ á®â­¨ ¨ ¡®«¥¥ à §. «ï â ª¨å á¨á⥬ å à ªâ¥à­ë ¡ë- áâயà®â¥ª î騥 ¯à®æ¥ááë ¢ "¯®£à ­¨ç­®¬ á«®¥", ª®â®àë¥ à §¢¨¢ îâáï ­ ä®­¥ ¬¥¤«¥­­ëå ¤¢¨¦¥­¨© [3, 72]. ¡ëç­® ¯®á«¥¤­¨¥ ¨ ¯à¥¤áâ ¢«ïîâ ¨­â¥à¥á ¤«ï ¨áá«¥¤®¢ ⥫ï, ®¤­ - ª® ¯à¨ ëå ¬¥â®¤ å ¨­â¥£à¨à®¢­¨ï ¯à¨å®¤¨âáï ¢ë¡¨à âì è £ h в ª¨¬ ®¡а §®¬, зв®¡л ­¥ ¯а®¨§®и« ¯®в¥ап гбв®©з¨- ¢®бв¨ ¨§-§ ¡лбвале ¤¢¨¦¥­¨©. 16 áᬮâਬ ⥯¥àì â ª ­ §ë¢ ¥¬ë¥ ­¥ï¢­ë¥ ¬¥â®¤ë. ।¯®«®¦¨¬, çâ® ¢ (6.56) ¨§- ¢¥áâ­® §­ 祭¨¥ x(tk+1) ¨ âॡã¥âáï ­ ©â¨ x(tk). 祢¨¤­®, çâ® ¢ "®¡à â­®¬" ¢à¥¬¥­¨ ãà ¢­¥­¨¥ (6.56) ¯à¨¬¥â ¢¨¤

§à¥è ï íâ® ­¥«¨­¥©­®¥ ãà ¢­¥­¨¥ ®â­®á¨â¥«ì­® xk+1 ¯®- «ãç ¥¬ ¨áª®¬®¥ ४ãà७⭮¥ ᮮ⭮襭¨¥

xk+1 = '(xk k): ᫨ ¨á室­®¥ ãà ¢­¥­¨¥ ¨¬¥¥â ¢¨¤ (6.58), ¯à¨å®¤¨¬ ª à §­®áâ­®¬ã ãà ¢­¥­¨î

ª®â®à®¥ ᮮ⢥âáâ¢ã¥â ¢ëç¨á«¥­¨î ¬ âà¨ç­®© íªá¯®­¥­âë ¯® ä®à¬ã«¥ ¤¥ (0 1). à ¢­¥­¨¥ (6.61) ãá⮩稢® ¤«ï «î- ¡®© ãá⮩稢®© á¨á⥬ë (6.58) ¯à¨ ¢á¥å h > 0. 17 ®¤®¡­ë¬

¯à¨¢¥¤¥­­ë¬ ¢ ¯ã­ªâ¥ 6.10.1. ­¥à ¢¥­á⢮¬ (6.55).

163

®¡à §®¬ ¬®¦­® ¯®«ãç¨âì ­¥ï¢­ë¥ ¬¥â®¤ë ¨­â¥£à¨à®¢ ­¨ï ¡®«¥¥ ¢ë᮪®£® ¯®à浪 , ᮮ⢥âáâ¢ãî騥 ¤à㣨¬ ¯¯à®ªá¨- ¬ æ¨ï¬ ¤¥. ¤® ®â¬¥â¨âì, çâ® ¨á¯®«ì§®¢ ­¨¥ ­¥ï¢­ëå ¬¥- ⮤®¢ ¯à¥¤¯®« £ ¥â à¥è¥­¨¥ ­ ª ¦¤®¬ è £¥ ¨­â¥£à¨à®¢ ­¨ï á¨á⥬ ­¥«¨­¥©­ëå «£¥¡à ¨ç¥áª¨å ãà ¢­¥­¨¥© ¢¨¤ (6.60).®¡é¥¬ á«ãç ¥ íâ® ¯à¨¢®¤¨â ª §­ ç¨â¥«ì­ë¬ ¢ëç¨á«¨â¥«ì- ­ë¬ § âà â ¬, ¯®í⮬㠯ਬ¥­¥­¨¥ ­¥ï¢­ëå ¬¥â®¤®¢ ®¡ëç­® íä䥪⨢­® ¨¬¥­­® ¤«ï ¦¥á⪨å á¨á⥬. ᫨ à áᬠâਢ - ¥âáï § ¤ ç ¬®¤¥«¨à®¢ ­¨ï «¨­¥©­ëå áâ 樮­ à­ëå á¨á⥬ ¢¨¤ (6.58), â® ¢ à¥è¥­¨¨ á¨á⥬ ãà ¢­¥­¨© (6.60) ­ ª ¦¤®© ¨â¥à 樨 ­¥â ­¥®¡å®¤¨¬®áâ¨. ¥©á⢨⥫쭮, ⮣¤ ¤®áâ - â®ç­® ¢ëç¨á«¨âì ¬ âà¨æë P Q ᮮ⢥âáâ¢ãî饩 (6.58) ¤¨á- ªà¥â­®© ¬®¤¥«¨ (6.14) ¯¥à¥¤ ­ ç «®¬ ¨­â¥£à¨à®¢ ­¨ï, § - ⥬ ¨á¯®«ì§®¢ âì ४ãà७â­ãî ä®à¬ã«ã (6.14) ¤«ï ¯®«ãç¥- ­¨ï ¯®á«¥¤®¢ ⥫쭮á⨠xk: í⮬ á«ãç ¥ ¯à¨¬¥­¥­¨¥ ¯- ¯à®ªá¨¬ 権 ¤¥ ¯®§¢®«ï¥â ¬­®£®ªà â­® 㬥­ìè¨âì ¢à¥¬ï ¢ëç¨á«¥­¨© ¯® áà ¢­¥­¨î á® áâ ­¤ àâ­ë¬¨ ¯à®æ¥¤ãà ¬¨ ¨­- ⥣à¨à®¢ ­¨ï. ®«¥¥ ¯®¤à®¡­ë¥ ᢥ¤¥­¨ï ® ç¨á«¥­­®¬ à¥è¥- ­¨¨ ¤¨ää¥à¥­æ¨ «ì­ëå ãà ¢­¥­¨© ¨ ãá«®¢¨ïå ãá⮩稢®á⨠ç¨á«¥­­ëå ¬¥â®¤®¢ ᮤ¥à¦ âáï, ­ ¯à¨¬¥à, ¢ à ¡®â å [13, 72],

â ª¦¥ ¢ ¯. 11.4.5. (á. 277), ¯®á¢ï饭­®¬ ¬¥â®¤ã ä㭪権ï¯ã­®¢ .

6.11.¡à â­ ï § ¤ ç { ª®­â¨­ã «¨§ æ¨ï ¤¨áªà¥â­ëå ¬®¤¥«¥©

áâ¥¬ë ª ¥¥ ­¥¯à¥à뢭®© (" ­ «®£®¢®©") ¬®¤¥«¨, ¤à㣨¬¨ á«®- ¢ ¬¨ { § ¤ ç ¯à¥®¡à §®¢ ­¨ï ãà ¢­¥­¨© (6.14) ª íª¢¨¢ «¥­â- ­ë¬ (¢ 㪠§ ­­®¬ ¢ëè¥ á¬ëá«¥) ãà ¢­¥­¨ï¬ (6.13). ª ïá­® ¨§ ¢ë襨§«®¦¥­­®£®, ¢ ãà ¢­¥­¨ïå á®áâ®ï­¨ï íâ®â ¯¥à¥å®¤ ¬®¦¥â ¡ëâì ¢ë¯®«­¥­ ¢ëç¨á«¥­¨¥¬ ¬ âà¨ç­®£® «®£ à¨ä¬ .áᬮâਬ íâ®â ¬¥â®¤ ¯®¤à®¡­¥¥, ¯®« £ ï, çâ® íª¢¨¢ «¥­â- ­ ï ­¥¯à¥à뢭 ï á¨á⥬ à ¡®â ¥â ¯à¨ ªãá®ç­®-¯®áâ®ï­­®¬ ¢å®¤­®¬ ¢®§¤¥©á⢨¨ ¢¨¤ (6.15). 18 «ï á¨áâ¥¬ë ¯¥à¢®£® ¯®à浪 ¯à¨ P = 1 ¬ âà¨æë A B ­¥¯à¥à뢭®© ¬®¤¥«¨ ¯à¨- ­¨¬ îâ ¢¨¤ A = 0 B = Q=T0:

«ï ¤à㣨å á¨á⥬ áâநâáï à áè¨à¥­­ ï ¬ âà¨æ

¢¥§¤®зª ¬¨ ®¡®§­ з¥­л ¯®¤¬ ва¨жл, §­ з¥­¨п ª®в®але ­¥ ¨б¯®«м§говбп.

6.12. ¤ ç¨ ¨ ã¯à ¦­¥­¨ï

1. 뢥á⨠ä®à¬ã«ë ¤«ï ¢ëç¨á«¥­¨ï ¬ âà¨ç­®© íªá¯®­¥­- âë eJt ¤«ï ¦®à¤ ­®¢®© ª«¥âª¨ J ¯à®¨§¢®«ì­®£® § ¤ ­­®£® ¯®- à浪 (á¬. á. 139).

2.®«ãç¨âì eAt ¢ ­ «¨â¨ç¥áª®¬ ¢¨¤¥ ¤«ï § ¤ ­­ëå ¢ ã¯à ¦­¥­¨¨ 1 ­ á. 126 ¬ âà¨æ. ( ª § ­¨¥ { ¨á¯®«ì§®¢ âì ¬¥â®¤, ®¯¨á ­­ë© ¢ ¯. 6.5.1.).

3.믮«­¨âì ã¯à ¦­¥­¨¥ ¯.2 á ¨á¯®«ì§®¢ ­¨¥¬ ¯à¥-

®¡à §®¢ ­¨ï ¯« á (á¬. á. 142).

4. ®á¯®«ì§®¢ âìáï ­ «¨â¨ç¥áª¨¬¨ ¢ëà ¦¥­¨ï¬¨ ¤«ï ¬ âà¨ç­®© íªá¯®­¥­âë (¯. 6.5.1.) ¨ ä®à¬ã« ¬¨ ¯¥à¥å®¤ ª ¤¨áªà¥â­ë¬ ¬®¤¥«ï¬ (¯.¯. 6.4.2. 6.6.) ¤«ï ¯®«ã祭¨ï â ¡«¨æë ᮮ⢥âáâ¢¨ï ¯¥à¥¤ â®ç­ëå ä㭪権 ⨯®¢ëå ­¥¯à¥à뢭ëå ¤¨­ ¬¨ç¥áª¨å §¢¥­ì¥¢ [15, 76] ¨ ¨å ¤¨áªà¥â­ëå ¬®¤¥«¥© ¯à¨ ¨á¯®«ì§®¢ ­¨¨ íªáâà ¯®«ïâ®à ­ã«¥¢®£® ¯®à浪 . à ¢­¨âì á ¯à¨¢¥¤¥­­ë¬¨ ¢ [15, 76] १ã«ìâ â ¬¨, ®á­®¢ ­­ë¬¨ ­ z-

¯à¥®¡à §®¢ ­¨¨.

5. ®ª § âì ¯¥à¥ç¨á«¥­­ë¥ ¢ ¯. 6.4.2. ᢮©á⢠¯¥à¥å®¤- ­®© ¬ âà¨æë.

6. 뢥á⨠ä®à¬ã«ã ¤«ï ®¯à¥¤¥«¥­¨ï ­ ç «ì­®£® á®áâ®- ï­¨ï x0 ¥á«¨ ¯à¨ t < 0 ¢å®¤­®¥ ¢®§¤¥©á⢨¥ u(t) 6 0 (äã­ªæ¨ï u(t) § ¤ ­ ¯à¨ ¢á¥å t). ᯮ«ì§®¢ âì ¨§«®¦¥­­ë© ¢ ¯. 6.3. á. 133, ¬¥â®¤.

7. â®çª¨ §à¥­¨ï à áᬮâ७­®© ¢ ¯. 6.3. § ¤ ç¨ ¤ âì ¨­â¥à¯à¥â æ¨î á¨âã 樨, ª®£¤ ¬ âà¨æ Q { ¢ë஦¤¥­­ ï.

165

7. {

7.1. á­®¢­ë¥ ®¯à¥¤¥«¥­¨ï

®­пв¨п г¯а ¢«п¥¬®бв¨ ¨ ­ ¡«о¤ ¥¬®бв¨ п¢«повбп ®¤­¨¬¨ ¨§ ®б­®¢­ле ¯®­пв¨© в¥®а¨¨ г¯а ¢«¥­¨п. ᮤ¥а¦ в¥«м- ­®¬ га®¢­¥ г¯а ¢«п¥¬®бвм ®§­ з ¥в ¯а¨­ж¨¯¨ «м­го ¢®§- ¬®¦­®бвм ¯а¨¢¥¤¥­¨п б¨бв¥¬л ¢ «о¡®¥ § ¤ ­­®¥ б®бв®п­¨¥,

­ ¡«î¤ ¥¬®áâì { ¢®§¬®¦­®áâì ®¯à¥¤¥«¥­¨ï á®áâ®ï­¨ï á¨- áâ¥¬ë ¯® १ã«ìâ â ¬ ¨§¬¥à¥­¨©. ⨠᢮©á⢠¢¥áì¬ áã- é¥á⢥­­ë ¤«ï ¯®áâ஥­¨ï à ¡®â®á¯®á®¡­ëå á¨á⥬ ¢â®-

¬ â¨ç¥áª®£® ã¯à ¢«¥­¨ï. ਢ¥¤¥¬ ­¥ª®â®àë¥ ®¯à¥¤¥«¥­¨ï [3, 30, 44, 47, 83].

¯à¥¤¥«¥­¨¥ 1. ®áâ®ï­¨¥ x ¤®á⨦¨¬® ¨§ á®áâ®ï­¨ï

­¥ ¤®á⨦¨¬®©), ¥á«¨ ã ­¥¥ ª ¦¤®¥ á®áâ®ï­¨¥ ¤®á⨦¨¬® ¨§ «î¡®£® ¤à㣮£®. à㣨¬¨ á«®¢ ¬¨, ã ¯®¤®¡­ëå á¨á⥬ ­¥â â ª¨å ®¡« á⥩ ¢ ¯à®áâà ­á⢥ á®áâ®ï­¨©, ¢ ª®â®àë¥ § ª®- ­¥ç­®¥ ¢à¥¬ï ­¥«ì§ï ¯®¯ áâì ¨§ «î¡ëå ¤àã£¨å ®¡« á⥩ ¯®¤ ¤¥©á⢨¥¬ ¤®¯ãá⨬®£® ã¯à ¢«¥­¨ï.

«ï «¨­¥©­ëå á¨á⥬ ¯®­ï⨥ ᨫ쭮á¢ï§­®á⨠¯¥à¥å®¤¨â

¢¯®­ï⨥ ¯®«­®© ã¯à ¢«ï¥¬®áâ¨.

ª з¥бв¢¥ ¯а¨¬¥а б¨бв¥¬л, ¤«п ª®в®а®© нв® б¢®©бв¢® ®вбгвбв¢г¥в, ¬®¦­® а бᬮва¥вм ®¡к¥ªв, б®бв®пй¨© ¨§ §¢¥- ­ б ­ блй¥­¨¥¬, ¯®б«¥¤®¢ в¥«м­® б®¥¤¨­¥­­®£® б ¯¥а¨®-

ª 㪠§ ­® ¢ ¯. 1.1. á®áâ®ï­¨¥ ¤¥â¥à¬¨­¨à®¢ ­­®© á¨áâ¥-

¬ë å à ªâ¥à¨§ã¥âáï ⥬, çâ® ¯à¨ § ¤ ­­®¬ ­ ç «ì­®¬ á®áâ®- ï­¨¨ x(t0) = x0 ¢ë室 á¨á⥬ë y(t1) ®¤­®§­ ç­® ®¯à¥¤¥«ï¥âáï ¥¥ ¢å®¤®¬ u(t) ­ ¯à®¬¥¦ã⪥ [t0 t1]: ¤­ ª® ¯® ®â­®è¥­¨î ª x0 íâ á¢ï§ì ¬®¦¥â ¡ëâì ­¥ ¢§ ¨¬­®-®¤­®§­ ç­®©: ¬®¦¥â

166

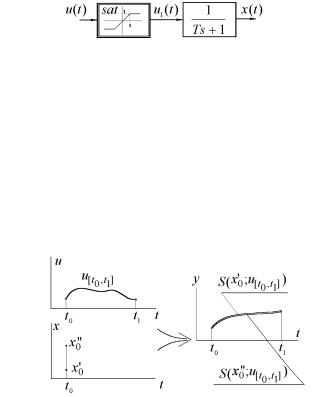
¨á. 7.1. ¨á⥬ á ­¥¤®á⨦¨¬ë¬¨ á®áâ®ï­¨ï¬¨.

®ª § âìáï, çâ® ¨¬¥¥âáï ¬­®¦¥á⢮ à §«¨ç­ëå á®áâ®ï­¨© â -

ª®¥, çâ® ¯à¨ «î¡®¬ ­ ç «ì­®¬ á®áâ®ï­¨¨ ¨§ í⮣® ¬­®¦¥á⢠¨ ¤«ï «î¡®£® ¢å®¤­®£® ¢®§¤¥©áâ¢¨ï ¯®«ãç îâáï ®¤¨­ ª®¢ë¥ ॠªæ¨¨.

¯à¥¤¥«¥­¨¥ 3. ®áâ®ï­¨ï x00 ¨ x000 ­ §ë¢ îâáï íª¢¨¢ - «¥­â­ë¬¨, x00 x000 , ¥á«¨ ¯à¨ «î¡®¬ ¢å®¤­®¬ ¯à®æ¥áᥠu(t) ¢ë- 室ë á¨áâ¥¬ë ¯à¨ ­ ç «ì­®¬ á®áâ®ï­¨¨ x(t0 ) = x00 ¨ x(t0 ) = x000 ᮢ¯ ¤ îâ (à¨á. 7.2).

¨á. 7.2. ª¢¨¢ «¥­â­ë¥ á®áâ®ï­¨ï, x00 x000 .

¯à¥¤¥«¥­¨¥ 4. ¨á⥬ ­ §ë¢ ¥âáï ।ãæ¨à®¢ ­­®©, ¥á«¨ ã ­¥¥ ­¥â à §«¨ç­ëå íª¢¨¢ «¥­â­ëå á®áâ®ï­¨©, â.¥. ª ¦¤®¥ á®áâ®ï­¨¥ íª¢¨¢ «¥­â­® ⮫쪮 á ¬®¬ã ᥡ¥. ­ë¬¨ á«®¢ - ¬¨, ¤«ï ।ãæ¨à®¢ ­­ëå á¨á⥬ ¯à¨ «î¡®¬ ¢å®¤¥ ¨ «î¡®¬ ­ ç «ì­®¬ á®áâ®ï­¨¨ ®â®¡à ¦¥­¨¥ ¢å®¤{á®áâ®ï­¨¥{¢ë室 ­¥

çâ® ª ¦¤®¥ á®áâ®ï­¨¥ ¤®á⨦¨¬® ¨§ «î¡®£® ¤à㣮£®, â.¥. ã¯- à ¢«ï¥¬®áâì ¤«ï ­¨å íª¢¨¢ «¥­â­ ᨫ쭮á¢ï§­®áâ¨.

167

¬ ¥ ç ­ ¨ ¥ 2. ᫨ ã¯à ¢«ï¥¬ ï «¨­¥©­ ï á¨á⥬

áâ 樮­ à­ , â® ¯®¯ ¤ ­¨¥ ¢ x ¬®¦­® ®¡¥á¯¥ç¨âì § «î¡®¥

§¤ ­­®¥ T > 0:

­¥ª®â®àëå ¯à¨«®¦¥­¨ïå â ª¦¥ ¯à¥¤áâ ¢«ï¥â ¨­â¥à¥á ã¯- à ¢«ï¥¬®áâì ¯® ¢ë室 ¬, ª®â®à ï ®§­ ç ¥â ¢®§¬®¦­®áâì ¯à¨- ¢¥¤¥­¨ï ¢ë室 ®¡ê¥ªâ ¢ § ¤ ­­ãî â®çªã. à ¡®â¥ [93] ¯à¨¢®¤¨âáï £à㯯 à §«¨ç­ëå ¯®­ï⨩ ã¯à ¢«ï¥¬®áâ¨, ªã¤ ªà®¬¥ 㪠§ ­­®£® ¯®­ïâ¨ï ®â­®á¨âáï â ª¦¥ ¢®§¬®¦­®áâì ¯à¨- ¢¥¤¥­¨ï ®¡ê¥ªâ ¨§ «î¡®© â®çª¨ ­¥ª®â®à®© § ¬ª­ã⮩ ®¡« -

á⨠¢ ¯à®¨§¢®«ì­ãî â®çªã í⮩ ®¡« á⨠¡¥§ ¢ë室 § ¥¥ £à ­¨æë, ¯¥à¥å®¤ ¨§ § ¤ ­­®© ®¡« á⨠¢ ®¡« áâì ¬¥­ì襩

t 2 [t0 t1 ] á«¥¤ã¥â: x(t0) = 0:

áâ¥á⢥­­®, çâ® ¤«ï áâ 樮­ à­ëå ¯à®¢¥àªã ãá«®¢¨© ã¯à ¢«ï¥¬®á⨠¨ ­ ¡«î¤ ¥¬®á⨠¬®¦­® ¢ë¯®«­ïâì ­¥ ¤«ï

¢á¥å t0 ⮫쪮 ¤«ï ®¤­®£® (­ ¯à¨¬¥à, t0 = 0): 1

¨¡®«¥¥ ᨫ쭮© ä®à¬®© ã¯à ¢«ï¥¬®á⨠ï¥âáï ­®à¬ - «¨§ã¥¬®áâì (­®à¬ «ì­®áâì). ®¢®àïâ, çâ® á¨á⥬ ­®à¬ «ì- ­ , ¥á«¨ ã¯à ¢«ï¥¬®áâì ¨¬¥¥âáï ¯® ª ¦¤®© ª®¬¯®­¥­â¥ ¢¥ªâ®- à ã¯à ¢«¥­¨ï. «ï á¨á⥬ ᮠ᪠«ïà­ë¬ ¢å®¤­ë¬ ¯à®æ¥áᮬ ã¯à ¢«ï¥¬®áâì ¨ ­®à¬ «¨§ã¥¬®áâì ᮢ¯ ¤ îâ.

®§¬®¦¥­ á«ãç © ç áâ¨ç­® ã¯à ¢«ï¥¬®© á¨á⥬ë, ã ª®â®- ன ­¥ ¢á¥ á®áâ®ï­¨ï ¤®á⨦¨¬ë ¨§ ­ã«¥¢®£® § ª®­¥ç­®¥ ¢à¥- ¬ï. à®áâà ­á⢮ á®áâ®ï­¨© â ª¨å á¨á⥬ ¬®¦¥â ¡ëâì ¯à¥¤- áâ ¢«¥­® ª ª ¯àï¬ ï á㬬 ¯®¤¯à®áâà ­á⢠ã¯à ¢«ï¥¬ëå ¨

1 «ï ­¥áâ 樮­ à­ëå á¨á⥬ à áᬠâਢ îâáï â ª¦¥ ¤®á⨦¨¬®áâì ¨ ¢®ááâ ­ ¢«¨¢ ¥¬®áâì [47], ª®в®ал¥ ¢ бв ж¨®­ а­®¬ б«гз ¥ б®¢¯ ¤ ов б®®в¢¥вбв¢¥­­® б г¯а ¢«п¥¬®бвмо ¨ ­ ¡«о¤ ¥¬®бвмо. ®бª®«мªг ¤ «¥¥ а бб¬ ва¨¢ овбп, ¢ ®б­®¢­®¬ бв ж¨®­ а­л¥ б¨бв¥¬л гª § ­­л¥ ¯®­пв¨п §¤¥бм ­¥ гв®з­повбп.

168

­¥ã¯à ¢«ï¥¬ëå á®áâ®ï­¨©. ­ «®£¨ç­® ¯à®áâà ­á⢮ á®áâ®- ï­¨© ç áâ¨ç­® ­ ¡«î¤ ¥¬®© á¨áâ¥¬ë ¬®¦­® à §¡¨âì ­ ¯®¤- ¯à®áâà ­á⢠­ ¡«î¤ ¥¬ëå ¨ ­¥­ ¡«î¤ ¥¬ëå á®áâ®ï­¨©.

¯à¥¤¥«¥­¨¥ 7. ­ §ë¢ ¥âáï áâ ¡¨«¨§¨à㥬®©, ¥á«¨ ã ­¥¥ ¯®¤¯à®áâà ­á⢮ ã¯à ¢«ï¥¬ëå á®áâ®ï­¨© ¯à¨­ ¤«¥¦¨â ¯®¤¯à®áâà ­áâ¢ã ãá⮩稢ëå á®áâ®ï­¨©.

â ¡¨«¨§¨à㥬®áâì ®§­ ç ¥â ¯à¨­æ¨¯¨ «ì­ãî ¢®§¬®¦- ­®áâì ¯®«ã祭¨ï ãá⮩稢®© § ¬ª­ã⮩ á¨á⥬ë: ᮡá⢥­- ­ë¥ ¤¢¨¦¥­¨ï ­¥ã¯à ¢«ï¥¬®© ç á⨠á¨áâ¥¬ë ¢ í⮬ á«ãç ¥ ãá⮩稢ë, ­ ­¥ãá⮩稢ãî ¯®¤á¨á⥬㠬®¦­® ¢®§¤¥©- á⢮¢ âì ᮮ⢥âáâ¢ãî騬 ã¯à ¢«¥­¨¥¬. 祢¨¤­®, çâ® ¯®«- ­®áâìî ã¯à ¢«ï¥¬ ï á¨á⥬ áâ ¡¨«¨§¨à㥬 (â ª ª ª ã ­¥¥ ­¥â ­¥ã¯à ¢«ï¥¬ëå á®áâ®ï­¨©). á⮩稢 ï á¨á⥬ ⮦¥

áâ ¡¨«¨§¨à㥬 , â ª ª ª ã ­¥¥ ¢á¥ ¯à®áâà ­á⢮ á®áâ®ï­¨© ï¥âáï ¯®¤¯à®áâà ­á⢮¬ ãá⮩稢ëå á®áâ®ï­¨©.

¯à¥¤¥«¥­¨¥ 8. ­ §ë¢ ¥âáï ®¡­ à㦨¢ ¥¬®©, ¥á«¨ ã ­¥¥ ¯®¤¯à®áâà ­á⢮ ­¥ã¯à ¢«ï¥¬ëå á®áâ®ï­¨© ¯à¨­ ¤«¥¦¨â ¯®¤¯à®áâà ­áâ¢ã ãá⮩稢ëå á®áâ®ï­¨©.

®«­®áâìî ­ ¡«î¤ ¥¬ë¥, â ª¦¥ ãáâ®©ç¨¢ë¥ á¨áâ¥¬ë ®¡- ­ à㦨¢ ¥¬ë.

¯à¥¤¥«¥­¨¥ 9. ®«­®áâìî ­ ¡«î¤ ¥¬ ï ¨ ¯®«­®áâìî ã¯à «ï¥¬ ï «¨­¥©­ ï á¨á⥬ ­ §ë¢ ¥âáï ­¥¢ë஦¤¥­­®©.

7.2. à¨â¥à¨¨ ã¯à ¢«ï¥¬®áâ¨

áá«¥¤®¢ ­¨¥ ã¯à ¢«ï¥¬®á⨠«¨­¥©­ëå áâ 樮­ à­ëå á¨á⥬ ¬®¦­® ¯à®¢®¤¨âì ­ ®á­®¢¥ àï¤ íª¢¨¢ «¥­â­ëå ªà¨â¥à¨¥¢.¨¦¥ ¤ ­ë ­¥ª®â®àë¥ ªà¨â¥à¨¨ ã¯à ¢«ï¥¬®á⨠áâ 樮­ à- ­ëå á¨á⥬ [3, 30, 83].

1. ( à¨â¥à¨© «¬ ­ ). âà¨æ ã¯à ¢«ï¥¬®áâ¨

áâà ­á⢮ ã¯à ¢«ï¥¬ëå á®áâ®ï­¨© ¯®à®¦¤ ¥âáï á⮫¡æ ¬¨

«¨­¥©­®-­¥§ ¢¨á¨¬ëå áâப (¨«¨ á⮫¡æ®¢) í⮩ ¬ âà¨æë. £® §­ ç¥- ­¨¥ ᮢ¯ ¤ ¥â â ª¦¥ á ¯®à浪®¬ ­ ¨¡®«ì襣® ®â«¨ç­®£® ®â ­ã«ï ¬¨­®à ¤ ­­®© ¬ âà¨æë [3, 53, 66, 115].

169

­¥§ ¢¨á¨¬ëå á⮫¡æ®¢, ¢á¥ ¯à®áâà ­á⢮ á®áâ®ï­¨© ï¥â-

3 ¯®¬­¨¬, çâ® £ãࢨ楢®© ­ §ë¢ ¥âáï ¬ âà¨æ , ¢á¥ ᮡá⢥­­ë¥ ç¨- á« ª®â®à®© ¨¬¥îâ ®âà¨æ ⥫ì­ë¥ ¢¥é¥á⢥­­ë¥ ç áâ¨.

4 â ª®¬ ¢¨¤¥ ªà¨â¥à¨© ä®à¬ã«¨àã¥âáï ¤«ï á¨á⥬ ᮠ᪠«ïà­ë¬ ã¯à ¢«¥­¨¥¬. ਠm > 1 ¯® í⮬㠪à¨â¥à¨î ­¥ ¤®«¦­® áãé¥á⢮¢ âì ¨­¢ ਠ­â­®£® ¯®¤¯à®áâà ­á⢠¬ âà¨æë A à §¬¥à­®áâ¨, ¬¥­ì襩, 祬 n ª®â®à®¥ ᮤ¥à¦ «® ¡ë ®¤­®¢à¥¬¥­­® ¢á¥ á⮫¡æë ¬ âà¨æë B:

¯à¥¤¥«¥­¨¥ ¨­¢ ਠ­â­®£® ¯®¤¯à®áâà ­á⢠¬ âà¨æë ¤ ­® ¢ëè¥ ¢ ¯. 3.1.2. ᭮᪠­ á. 83

170

¨á. 7.3. ­®­¨ç¥áª¨¥ ä®à¬ë ã¯à ¢«ï¥¬®á⨠( ) ¨ ­ ¡«î- ¤ ¥¬®á⨠(¡).

á¨áâ¥¬ë ¢á¥£¤ ¨¬¥¥â à¥è¥­¨¥ § ¤ ç ¬®¤ «ì­®£® ã¯à ¢«¥- ­¨ï ¯® á®áâ®ï­¨î { ®¡¥á¯¥ç¥­¨ï § ¤ ­­ëå §­ 祭¨© ª®íä- ä¨æ¨¥­â®¢ å à ªâ¥à¨áâ¨ç¥áª®£® ¬­®£®ç«¥­ § ¬ª­ã⮩ á¨- á⥬ë á ¯®¬®éìî ॣã«ïâ®à ¢ 楯¨ ®¡à â­®© á¢ï§¨ ¢¨¤

u(t) = ;Kx(t). 5

5. ¥ áãé¥áâ¢ã¥â ­¨ ®¤­®© ®â«¨ç­®© ®â ­ã«ï ¬ âà¨æë C â ª®©, çâ®¡ë ¯¥à¥¤ â®ç­ ï äã­ªæ¨ï W(s) = C(sI ; A);1B ⮦¤¥á⢥­­® (¤«ï ¢á¥å s) à ¢­ï« áì ­ã«î.

6. ¢¥­á⢮ CeAtB = 0 ¯à¨ ¢á¥å t t1 < t < t2 ¤«ï ­¥ª®â®à®£® C 2Rn ¢®§¬®¦­® ⮫쪮 ¯à¨ C = 0:

ã­ªæ¨ï ¢¥á (á¬. ¯. 6.2. á. 133) ¯®«­®áâìî ã¯à ¢«ï¥¬ëå á¨á⥬ á ®¤­¨¬ ¢ë室®¬ ®¡à é ¥âáï ¢ ­®«ì ­ ª®­¥ç­®¬ ¨­- â¥à¢ «¥ ⮫쪮 ¢ âਢ¨ «ì­®¬ á«ãç ¥ C = 0:

7. 믮«­¥­¨¥ ᮮ⭮襭¨© AT z = 0z ¨ BT z = 0 ¤«ï ­¥ª®â®à®£® 0 2 C ¨ z 2Rn ¢®§¬®¦­® «¨èì ¯à¨ z = 0 [30, 83].

âáî¤ , ¢ ç áâ­®áâ¨, ¢ë⥪ ¥â á«¥¤ãî騩 ªà¨â¥à¨©:

8. ᫨ ¯ à (A B) ã¯à ¢«ï¥¬ , â® ¤«ï «î¡®© m n- ¬ âà¨æë K ¯ à (A + BK B) â ª¦¥ ã¯à ¢«ï¥¬ .

5®«¥¥ ¯®¤à®¡­® à¥è¥­¨¥ í⮩ § ¤ ç¨ ¤«ï ᪠«ïà­®£® ã¯à ¢«¥­¨ï

àáᬠâਢ ¥âáï ­¨¦¥ ¢ £« ¢¥ 9.

171