
Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления
.pdf

í⮩ ¬®¤¥«¨, ¢®§¬ãé¥¨ï ¯à¥¤áâ ¢«îâáï ª ª à¥è¥¨ï á¨áâ¥- ¬ë ®¤®à®¤ëå ¤¨ää¥à¥æ¨ «ìëå (¨«¨ à §®áâëå) ãà ¢- ¥¨© á ¨§¢¥áâ묨 ª®íää¨æ¨¥â ¬¨ ¨ ¥¨§¢¥áâ묨 ç «ì- 묨 ãá«®¢¨ï¬¨. íâ¨å ç «ìëå ãá«®¢¨ïå ¨ ᮤ¥à¦¨âáï ¢áï ¥®¯à¥¤¥«¥®áâì ®â®á¨â¥«ì® ¢¥è¨å ¢®§¤¥©á⢨©. 7ª¨¬ ®¡а §®¬, ¢®§¬гй¥¨п ¨ ¯®¬¥е¨ ¯а¥¤бв ¢«повбп, ª ª ¢ле®¤л ¥ª®в®а®© ¢в®®¬®© ¤¨ ¬¨з¥бª®© б¨бв¥¬л б § - ¤ л¬¨ га ¢¥¨п¬¨ ¨ ¥¨§¢¥бвл¬ з «мл¬ б®бв®п¨¥¬.в¥¬ ¬®¤¥«м ¢¥и¨е ¢®§¤¥©бв¢¨© ®¡к¥¤¨п¥вбп б ¬®¤¥«мо ®¡к¥ªв г¯а ¢«¥¨п ¨ ¤«п ¯®«гз¥®© à áè¨à¥®© á¨á⥬ë áâநâáï ¡«î¤ ⥫ì. ®«ãç¥ë¥ á ¯®¬®éìî ¥£® ®æ¥- ª¨ ᮤ¥à¦ â ª ª ᮡá⢥® ®æ¥ª¨ á®áâ®ï¨ï ®¡ê¥ªâ , â ª ¨ ®æ¥ª¨ ¢¥è¨å ¢®§¤¥©á⢨© 8.
®¤å®¤ ª á¨â¥§ã á¨á⥬ ã¯à ¢«¥¨ï ®á®¢¥ ¯®áâ㫨- ஢ ¨ï ¤¨ ¬¨ç¥áª¨å ¬®¤¥«¥© ¤«ï ®â¤¥«ìëå ¯®¤á¨á⥬ ¨
ᨣ «®¢ ¢ áâ®ï饥 ¢à¥¬ï 襫 è¨à®ª®¥ ¯à¨¬¥¥¨¥ ¨
§ë¢ ¥âáï "¯à¨æ¨¯®¬ ¢ãâà¥¨å ¬®¤¥«¥©" ("internal model principle"). «ï ¯®áâ஥¨ï íä䥪⨢ëå «£®à¨â¬®¢ ¯à®¥ª- â¨à®¢ ¨ï, ®æ¥¨¢ ¨ï, ã¯à ¢«¥¨ï á¨á⥬ ¬¨ ¬®¤¥«¨ ¢ ¢¨¤¥ ãà ¢¥¨© á®áâ®ï¨ï ¬®£ãâ § ¤ ¢ âìáï ¥ ⮫쪮 ¤«ï ¢®§¬ã-
é îé¨å ¢®§¤¥©á⢨©, ® ¨ ¤«ï ¯®¬¥å ¨§¬¥à¥¨©, ª®¬ ¤ëå ᨣ «®¢ ("íâ «®ë¥ ¬®¤¥«¨"), ¤¨ ¬¨ª¨ ¨§¬¥¥¨ï ¯ à - ¬¥â஢ ®¡ê¥ªâ ¨ â.¤. 9
®áâ â®ç® ¯à®áâ® ¯à®æ¥¤ãà á¨â¥§ ¢ë£«ï¤¨â, ¥á«¨ ¢¥è- ¨¥ ¯à®æ¥ááë ¬®¦® ¯à¥¤áâ ¢¨âì ª ª ª¢ §¨¬®£®ç«¥ë { ¢ë-
|
N |
|
|
à ¦¥¨ï ¢¨¤ |
X |
e itPi(t) £¤¥ i 2 C |
{ ¨§¢¥áâë¥ ¯®áâ®ïë¥, |
i=1
Pi(t) - ¬®£®з«¥л б § ¤ л¬¨ ª®ндд¨ж¨¥в ¬¨. о¤ ®в- ®бпвбп бв¥¯¥л¥ дгªж¨¨, £ ମ¨ª¨ б § ¤ ®© з бв®в®©,
нªб¯®¥вл б § ¤ л¬ ¯®ª § в¥«¥¬ § вге ¨п, ¯а®¨§¢¥¤¥¨п £ ମ¨ª нªб¯®¥вл ¨ «¨¥©л¥ ª®¬¡¨ ж¨¨ нв¨е дгª- ж¨©. ®¤¥«п¬¨ ¨бв®з¨ª®¢ в ª¨е ¯а®ж¥бб®¢ п¢«повбп «¨¥©- л¥ ¤¨дд¥а¥ж¨ «мл¥ га ¢¥¨п б ¯®бв®пл¬¨ ª®ндд¨ж¨- ¥в ¬¨. бᬮва¨¬ ¯а®ж¥¤гаг ®ж¥¨¢ ¨п ¤«п нв®£® б«гз п
7 «ãç © ¥¨§¢¥áâëå ¯ à ¬¥â஢ ¬®¤¥«¨ á।ë à áᬠâਢ ¥âáï ¢ à ¬ª å ⥮ਨ ¤ ¯â¨¢®£® ®æ¥¨¢ ¨ï (á¬. £« ¢ã 12 ¨ [93, 76, 103, 106]).
8 áâ¥á⢥®, âॡã¥âáï ¯®« ï ¡«î¤ ¥¬®áâì à áè¨à¥®© á¨á⥬ë.
9 ««îáâà 権 ¯à¨¬¥¥¨ï í⮣® ¯à¨æ¨¯ ¬®¦¥â á«ã¦¨âì ¨ «£®- à¨â¬ ¯¥à¥å®¤ ª ¤¨áªà¥â®© ¬®¤¥«¨, ®¯¨á ë© ¢ 6.6.
193
¡®«¥¥ ¯®¤à®¡®.
ãáâì ¢¥è¨¥ ¢®§¤¥©á⢨ï f(t) v(t) ¬®¦® ¯à¥¤áâ ¢¨âì ¢ ¢¨¤¥ ¢ë室ëå ¯à®æ¥áᮢ «¨¥©®© á¨á⥬ë, § ¤ ®© ãà ¢-
¥¨ï¬¨
xs(t) = As(t)xs(t) |
ys(t) = Csxs(t) xs(t0 ) = xs0 |
t |
t0: (8.15) |
||
¤¥áì xs(t) 2 Rns |
{ ¢¥ªâ®à á®áâ®ï¨ï "á।ë", |
ys(t) 2 Rn+l |
|||
- ¢ë室 ¬®¤¥«¨ |
¨áâ®ç¨ª |
¢®§¬ã饨© { ¢¥ªâ®à |
¢¥è¨å |
||
|
|
|
|
|
|
¯® ®â®è¥¨î ª ®¡ê¥ªâã ¢®§¤¥©á⢨©\ ys(t) = colff (t) v(t)g |
|||||
|
|
|
Cf |
|
|
As Cs { ¨§¢¥áâë¥ ¬ âà¨æë, Cs = Cv \ Cf Cv |
{ ¯®¤¬ - |
||||
âà¨æë à §¬¥à®¢ n ns |
l ns |
®¯à¥¤¥«ïî騥 á¢ï§ì ¬¥¦¤ã á®- |
|||
áâ®ï¨¥¬ xs(t) ¬®¤¥«¨ ¢¥è¨å ¢®§¤¥©á⢨© ¨ ¢®§¬ã饨ﬨ
f(t) ¯®¬¥å ¬¨ v(t) ¢ (8.1). ç «ì®¥ á®áâ®ï¨¥ xs0 á¨áâ¥- ¬ë (8.15), ª ª ¨ (8.1), áç¨â ¥âáï ¥¨§¢¥áâë¬. ¢¥¤¥¬ à á- è¨à¥ë© ("ᮢ®ªã¯ë©") ¢¥ªâ®à á®áâ®ï¨ï ®¡ê¥ªâ ¨ á।ë
|
xs(t)) 2 Rn+ns : ¡ê¥¤¨ïï ãà ¢¥¨ï (8.1), (8.15), |
|||||
x(t) = (x(t) |
||||||
¯®«ã稬 ãà ¢¥¨ï à áè¨à¥®© á¨áâ¥¬ë ¢ ¢¨¤¥ |
||||||
|
|
|
|
|
x(t0) = x0 t t0 (8.16) |
|
x(t) = Ax(t) + Bu(t) |
y(t) = Cx(t) |
|||||
¢ ª®â®àëå ¬ âà¨æë |
|
|
|
¨¬¥ов б«¥¤гойго ¡«®зго |
||
A |
B |
C |
||||
áâàãªâãàã: |
|
|
|
|
|
|
|
A |
Cf |
|
|
B |
|
A = |
0ns n As |
B |
= |
0ns m |
C = [C Cv]: |
|
áè¨à¥ ï á¨á⥬ |
(8.16) à áᬠâਢ ¥âáï ª ª ¥ª®â®àë© |
|||||
®¢ë© ®¡ê¥ªâ ¯®à浪 n = n + ns ¤«ï ª®â®à®£® áâநâáï - ¡«î¤ ⥫ì (8.3).
ந««îáâà¨à㥬 ¨§«®¦¥®¥ ¯à¨¬¥à¥.
áᬮâਬ ã¯à®é¥ãî ¬®¤¥«ì 㣫®¢®£® ¤¢¨¦¥¨ï ¨á-
ªãáá⢥®£® á¯ã⨪ |
¥¬«¨ ( ) ¯® ªà¥ã |
|
||
Jx |
d2 |
= u(t) + M (t) |
(8.17) |
|
dt2 |
||||
|
|
|
||
£¤¥ Jx { ¬®¬¥â ¨¥à樨 ®â®á¨â¥«ì® ¯à®¤®«ì®© ®á¨,(t) { 㣮« ªà¥ , u(t) { ã¯à ¢«ïî騩 ¬®¬¥â, M(t) { ¢®§- ¬ãé î騩 ¬®¬¥â. ãáâì ¤®áâ㯠¨§¬¥à¥¨î 㣫®¢ ï ᪮-
à®áâì ªà¥ !x(t) = (t): 票ï u(t) â ª¦¥ áç¨â îâáï ¨§- ¢¥áâ묨. ®¤«¥¦¨â ®æ¥¨¢ ¨î ¥¨§¬¥àï¥¬ë© ¬®¬¥â ¢®§- ¬ã饨© M (t): 㤥¬ ¯®« £ âì ¥£® «¨¥©®© äãªæ¨¥© ¢à¥-
¬¥¨ M(t) = M0 + V t ¯à¨ç¥¬ M0 V { ¥¨§¢¥áâë¥ ¢¥«¨ç¨ë.
194

â®â ¯à®æ¥áá ¬®¦® ¯à¥¤áâ ¢¨âì ª ª à¥è¥¨¥ á¨áâ¥¬ë ®¤®- தëå ¤¨ää¥à¥æ¨ «ìëå ãà ¢¥¨©
|
|
|
|
|
_ |
|
= |
V (t) |
|
|
|
||
|
|
|
|
|
M (t) |
|
|
|
(8.18) |
||||
|
|
|
|
V_ (t) |
|
= |
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
á ¥¨§¢¥áâ묨 ç «ì묨 ãá«®¢¨ï¬¨ M(0) |
V (0): ¢¥¤¥¬ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¢¥ªâ®à á®áâ®ï¨ï á¨á⥬ë "®¡ê¥ªâ { á। " x(t) = [!x(t) M(t) |
|||||||||||||
V (t)]T : ë室 á¨á⥬ë y(t) = !x(t): ª¨¬ ®¡à §®¬, ¯à¨å®¤¨¬ |
|||||||||||||
ª ãà ¢¥¨ï¬ á®áâ®ï¨ï ¢¨¤ |
(8.16), ¢ ª®â®àëå |
|
|
||||||||||
|
|
0 |
1 |
0 |
|
|
|
|
1 |
|
|
|
|
|
4 |
Jx |
5 |
|
|
4 |
Jx |
5 |
|
0 0]: |
(8.19) |
||
0 |
0 |
0 |
|
0 |
|||||||||
|
|
|
|
||||||||||
A = 2 |
0 |
0 |
1 |
3 B = |
2 |
0 |
3 C = [1 |
||||||
¡à ⨬áï ª á¨â¥§ã ¡«î¤ ⥫ï. ¡«î¤ â¥«ì ¯®«®£® |
|||||||||||||
¯®à浪 (8.3) |
¤«ï á¨á⥬ë (8.17), |
(8.18) ¨¬¥¥â à §¬¥à®áâì |
|||||||||||
n = 3: ¥à¥¬¥ë¥ á®áâ®ï¨ï ¡«î¤ ⥫ï x1(t) x1 |
(t) x1(t) |
|
||||||||||||||||||||
á«ã¦ ⠮楪 ¬¨ ¯¥à¥¬¥ëå !x(t) M (t) V (t) ᮮ⢥âá⢥- |
|
|||||||||||||||||||||
®. «ï ®¯à¥¤¥«¥¨ï âà¥å¬¥à®£® ¢¥ªâ®à ¯ à ¬¥â஢ L - |
|
|||||||||||||||||||||
¡«î¤ â¥«ï ©¤¥¬ å à ªâ¥à¨áâ¨ç¥áª¨© ¬®£®ç«¥ det(sI3 ; |
|
|||||||||||||||||||||
|
|
|
|
|
3 |
|
2 |
|
|
l2 |
|
|
|
l3 |
|
|
|
|
|
|
||
A |
|
+ LC) = s |
|
|
+ l1s + |
Jx s + Jx : à¨à ¢ï¢ ¥£® ª áâ ¤ à⮬ã |
|
|||||||||||||||
¬®£®ç«¥ã ââ¥à¢®àâ |
|
|
|
|
|
|
|
|
|
|
||||||||||||
A |
|
(s) = s3 |
+ 2 s2 |
+ 2 2s |
+ 3 |
¯®«ã稬 ¢ëà ¦¥¨ï ¤«ï l |
: |
|||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
0 |
|
|
|
i |
|
||||
l |
1 |
|
|
= 2 |
l |
2 |
= 2J |
x |
2 |
|
l |
|
= J |
x |
3: |
à ¬¥âà § ¤ ¥â ¡ë- |
|
|||||
|
|
|
|
0 |
|
|
|
0 |
|
3 |
|
|
|
0 |
0 |
|
|
|||||
áâத¥©á⢨¥ ¡«î¤ ⥫ï. à¥¬ï ¯¥à¥å®¤®£® ¯à®æ¥áá á®- |
|
|||||||||||||||||||||
áâ ¢«ï¥â ¯à¨¬¥à® 5= 0 |
: à §¢¥àã⮩ ä®à¬¥ ãà ¢¥¨ï - |
|
||||||||||||||||||||
¡«î¤ ⥫ï (8.3) ¯à¨¨¬ îâ ¢ ¤ ®¬ á«ãç ¥ ¢¨¤ |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
^ |
|
|
|
|
|
|
|
|
|
|
|
> |
!^x(t) = ;l1!^x(t) + M (t)=Jx + l1!x(t) + u(t)=Jx |
|
||||||||||||||||
|
|
|
|
^ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< |
^ |
|
|
= ;l2 |
|
|
|
|
^ |
|
|
|
|
(8.20) |
||||
|
|
|
|
8 M(t) |
|
|
!^x(t) + V (t) + l2!x(t) |
|||||||||||||||
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> V (t) = ;l3 |
!^x(t) + l3!x(t): |
|
|
|
||||||||||||||
«ï ¨««îáâà 樨 |
|
à¨á. |
8.3 (ᯫ®è ï «¨¨ï) ¯à¨¢¥¤¥ë |
|
||||||||||||||||||
१ã«ìâ âë ¬®¤¥«¨à®¢ ¨ï á¨á⥬ë (8.17), (8.20) ¯à¨ á«¥¤ã- |
|
|||||||||||||||||||||
îé¨å § 票ïå ¯ à ¬¥â஢ ®¡ê¥ªâ |
¨ ¢®§¤¥©á⢨©: |
|
|
|||||||||||||||||||
Jx=54.3 ª£ ¬2, M(0)=0.25 ¬, V |
= |
5 10;3 ¬/á. |
ë¡à ® |
|||||||||||||||||||
0=0.5 1/c. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
195
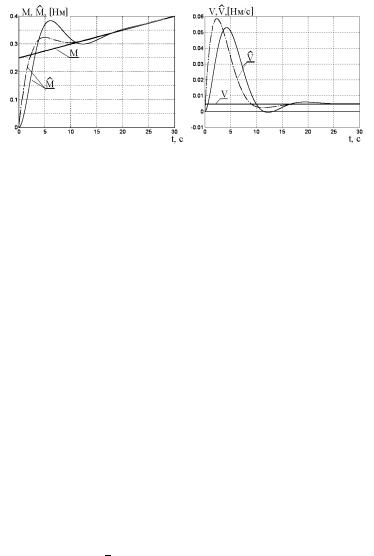
¨á. 8.3. à®æ¥áá ®æ¥¨¢ ¨ï ¢®§¬ã饨©.
«ï ¬®¤¥«¨à®¢ ¨ï ¨á¯®«ì§®¢ á«¥¤ãîé ï MATLAB- ¯à®£à ¬¬
à®£à ¬¬ ¬®¤¥«¨à®¢ ¨ï ¡«î¤ ⥫ï á®áâ®ï¨ï ¨ ¢®§¬ã饨© ¤«ï ¯® «¬ ã.
x0 |
|
=[0, 0, 0]'v |
x0=[0 0.25 0.005]'v |
|
|||||||||
|
|||||||||||||
{ § ¤ ¨¥ ç «ì®£® à áè¨à¥®£® ¢¥ªâ®à |
|||||||||||||
x = colf x M V g\ |
|||||||||||||
A=[0 1/J 0v 0 0 1v 0 0 0]v |
|
|
|
|
|||||||||
B=[1/Jv 0v 0]v |
C=[1 0 0]v |
|
|
|
|
||||||||
{ ¢¢®¤ ¬ âà¨æ |
|
|
|
|
|
|
|
||||||
A B C ãà ¢¥¨© á®áâ®ï¨ï à áè¨à¥®£® |
|||||||||||||
®¡ê¥ªâ \ |
|
|
|
|
|
|
|
|
|
|
|||
Om=0.5v |
l1=2*Omv l2=2*J*Om 2v |
l3=J*Om 3v |
|||||||||||
{ ¢¢®¤ § 票ï 0 ¨ ¢ëç¨á«¥¨¥ ª®íää¨æ¨¥â®¢ ®¡à ⮩ |
|||||||||||||
á¢ï§¨ l1 l2 l3 |
\ |
|
|
|
|
|
|
|
b |
b |
|||
L=[l1v l2v l3]v |
A |
|
=A-L*Cv |
B |
|
=Bv |
|
||||||
|
|
|
|||||||||||
{ ä®à¬¨à®¢ ¨¥ ¬ âà¨æ ãà ¢¥¨© (8.20)\ |
|
||||||||||||
Ae=[A, zeros(3,3)v L*C, A |
|
]v |
Be=[Bv B]v Ce=[C, -C]v |
||||||||||
|
|||||||||||||
{ä®à¬¨à®¢ ¨¥ ¬ âà¨æ ®¡ê¥¤¨¥®© á¨á⥬ë (8.17), (8.20)\ xe0=[x0v x0 ]v
{§ ¤ ¨¥ ç «ì®£® á®áâ®ï¨ï á¨á⥬ë (8.17), (8.20)\ t=0:0.01:30v u=zeros(size(t))v
{ § ¤ ¨¥ ¨â¥à¢ « ¬®¤¥«¨à®¢ ¨ï ¨ ä®à¬¨à®¢ ¨¥ ¢å®¤-
®£® ¢®§¤¥©á⢨ï\
[y,xe] =lsim(Ae,Be,Ce,0,u,t,xe0)v
{ ¬®¤¥«¨à®¢ ¨¥\ plot(t,xe(:,2),'w',t,xe(:,5),'.w'),grid plot(t,xe(:,3),'w',t,xe(:,6),'.w'),grid
196
{ ¢ë¢®¤ £à 䨪®¢.
áᬮâਬ ⥯¥àì ¨á¯®«ì§®¢ ¨¥ ¤«ï à¥è¥¨ï í⮩ § ¤ - ç¨ ¡«î¤ ⥫ï 㥡¥à£¥à (á¬. 8.3. á. 187).
ª ç¥á⢥ ¨á室®© ¬®¤¥«¨ ®¡ê¥ªâ ¢®§ì¬¥¬ ãà ¢¥¨ï à áè¨à¥®© á¨á⥬ë (8.17), (8.18) á ¬ âà¨æ ¬¨ (8.19). 10 ®- £« á® ¨§«®¦¥®¬ã á. 191 «£®à¨â¬ã, ãà ¢¥¨ï á®áâ®ï- ¨ï á¨á⥬ë á ç « ¯à¨¢®¤ïâáï ª ¢¨¤ã . «ï í⮣®, ¢
ᮮ⢥âá⢨¨ á ®¡é¥© ä®à¬ã«®© (3.13) (á¬. á. 88, 3.2.3.) áâà®- |
||||||||||||||||||||||||||
|
|
~ ~ |
âॡ㥬®£® ª ®¨ç¥áª®£® ¢¨¤ . ®«ã稬 |
|||||||||||||||||||||||
ïâáï ¬ âà¨æë A, C |
||||||||||||||||||||||||||
|
|
|
|
6 |
|
0 |
|
|
0 |
0 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
~ |
|
0 |
|
|
1 |
0 |
|
~ |
|
= [0 0 1]: |
|
|
|
|
|
|
|||||||
|
|
A = 2 1 0 0 3 C |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
~ |
©¤¥¬ ¬ âà¨æë ¡«î¤ ¥¬®á⨠|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Q ¨á室®© á¨áâ¥¬ë ¨ Q { |
||||||||||||||||||||||||||
á¨áâ¥¬ë ¢¨¤ |
, ®âªã¤ |
¯®«ã稬 ¬ âà¨æ㠯८¡à §®¢ - |
||||||||||||||||||||||||
¨ï T : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
0 |
|
|
|
|
|
|
0 |
7 |
|
|
|
6 |
0 |
0 |
|
1 |
7 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Q = 2 0 |
;1 |
|
|
|
|
|
|
~ |
= 2 0 1 0 3 |
|
|||||||||||||||
|
Jx |
|
|
|
|
|
|
0 3 Q |
|
|||||||||||||||||
|
|
4 |
0 |
0 |
|
|
|
|
|
Jx ;1 |
5 |
|
|
|
4 |
1 |
0 |
|
0 |
5 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
6 |
0 |
0 |
|
Jx ;1 |
7 |
|
|
|
|
|
|
|||
|
|
|
|
~;1 |
|
|
|
1 |
0 |
|
|
0 |
|
|
|
|
|
|
|
|||||||
|
|
T = Q |
Q |
= 2 0 |
Jx |
|
|
|
0 3 : |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
롥६ ¦¥« ¥¬ë© ¢¨¤ å à ªâ¥à¨áâ¨ç¥áª®£® ¬®£®ç«¥ |
||||||||||||||||||||||||||
¡«î¤ â¥«ï ¢ ä®à¬¥ ¬®£®ç«¥ |
ââ¥à¢®àâ |
|
¢â®à®£® ¯®- |
|||||||||||||||||||||||
à浪 A |
(s) = s2 + p |
|
|
s |
+ 2 |
£¤¥ ¯ à ¬¥âà |
|
§ ¤ ¥â ¡ë- |
||||||||||||||||||
2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
= p |
|
|
|
|
|
|
0 |
|
|
||
áâத¥©á⢨¥ ¡«î¤ ⥫ï. ®£¤ |
|
1 |
2 |
|
|
2 |
= 2 |
: |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
||
®áâந¬ ¬ âà¨æ㠯८¡à §®¢ ¨ï P ª 㪠§ ®¬ã ¢ ¯. |
||||||||||||||||||||||||||
8.3. ª ®¨ç¥áª®¬ã ¢¨¤ã |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
6 |
1 0 ; 0 2 |
|
7 |
|
|
|
|
6 |
1 0 0 2 |
7 |
|||||||||||||||
|
0 0 |
; |
|
1 |
|
|
|
|
|
|
|
0 0 |
|
|
|
1 |
||||||||||
P = 2 |
0 1 |
p |
2 |
0 |
3 P;1 = 2 |
0 1 |
p |
2 |
0 |
3 : |
||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
10 «ï ã¯à®é¥¨ï ®¡®§ 票© ¤ «¥¥ ¢ ¤ ®¬ ¯à¨¬¥à¥ § ª |
ã ¬ âà¨æ |
|||||||||||||||||||||||||
(8.19) ®¯ã᪠¥âáï.
197

¥¯¥àì ¯®áâந¬ ¬ âà¨æë
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 2 |
|
; |
p |
|
|
|
|
|
0 3 |
|
|
|
|
|
|
; |
0 |
2 |
J |
x ;1 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
~ |
;1 |
|
|
6 |
|
|
; |
|
|
|
|
|
|
|
2 |
|
7 |
|
|
6 |
|
|
|
|
|
|
|
|
|
7 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
;1 |
|||||||||||
|
= |
2 1 |
|
|
|
|
p2 0 |
|
|
|
|
|
0 |
|
3 |
|
|
|
|
|
p2 0 Jx |
3 |
||||||||||||||||||||||||||||||
A = P AP |
|
|
; |
|
; |
|
|
|
B = 2 |
; |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
1 |
|
|
|
p2 0 |
|
|
|
|
|
|
|
Jx ;1 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
§ ¬ âà¨æë A ¯®¤¬ âà¨æã |
A ¢â®à®£® ¯®à浪 , |
|
|
â ª¦¥ ¢ë- |
||||||||||||||||||||||||||||||||||||||||||||||||
¤¥«¨¬ ¯¥à¢ë¥ ¤¢¥ áâப¨ ¬ âà¨æë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
B ¨§ ª®â®àëå ®¡à §ã¥¬ |
||||||||||||||||||||||||||||||||||||||||||||||||||||
¢¥ªâ®à-á⮫¡¥æ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
B: ®«ã稬 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
0 |
|
|
|
0 2 |
|
|
|
|
|
|
|
|
|
|
|
|
; |
p |
|
|
|
|
|
|
0 3 |
|
|
|
|
|
|
|
; |
0 2 |
J |
x ;1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
A = " |
1 |
; |
p |
2 |
0 # a3 = " |
; |
0 2 |
|
|
# B |
= " |
; |
p |
2 |
0 Jx ;1 # : |
|||||||||||||||||||||||||||||||||||||
à¨å®¤¨¬ ª ãà ¢¥¨ï¬ ¡«î¤ â¥«ï ¢â®à®£® ¯®à浪 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
x1 |
(t) = 0 2x1 |
(t) |
|
|
|
p |
|
0 3!x (t) |
|
|
|
0 2Jx ;1u(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
; |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
; |
|
|
|
|
|
|
|
;1 |
|
|
|
|
|
|
|
|
|
(8.21) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
x2(t) = x1(t) ; p2 0 x2 (t) ; |
0 |
|
!x |
(t) ; p2 0 Jx |
|
|
|
u(t): |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
«¥¥ áä®à¬¨à㥬 ¢¥ªâ®à x(t) = colfx(t) !x (t)g: «ï ¯®«ãç¥- ¨ï ®æ¥ª¨ á®áâ®ï¨ï ¢ ¨á室®¬ ¡ §¨á¥ (8.17), (8.18) ©¤¥¬ ¬ âà¨æã ®¡à ⮣® ¯¥à¥å®¤ Tb { á ç « ®â x ª x~ § ⥬ { ª
x: |
|
0 |
|
0 |
1 |
|
|
|
|
|
6 |
|
|
7 |
|
||||
|
|
|
|
|
|
|
|
||
Tb = T;1P;1 |
= 2 0 |
Jx |
Jx p |
2 |
0 3 : |
^ |
|||
|
4 |
Jx |
0 |
Jx 0 2 |
^5 |
||||
|
|
|
|
||||||
¥ªâ®à x^(t) = Tbx(t) ᮤ¥à¦¨â ®æ¥ª¨ !^x (t) M (t) ¨ V (t).
¬ ¢¨¤¥ ®æ¥ª |
¯à®æ¥áá ¢®§¬ã饨© ¢ëà ¦ ¥âáï á®®â®- |
|||||
襨ﬨ |
|
|
|
|
|
|
|
^ |
|
|
|
|
|
|
|
|
|
|
||
|
M(t) = Jx x1(t) + Jx p2 0 x2(t) |
(8.22) |
||||
^ |
2 |
x2(t): |
||||
|
||||||
V (t) = Jx !x(t) + Jx 0 |
|
|||||
®¢®ªã¯®áâì |
ãà ¢¥¨© (8.21), (8.22) ®¯¨áë¢ ¥â ¡«î¤ - |
|||||
⥫ì 㥡¥à£¥à |
¤«ï à áᬠâਢ ¥¬®© § ¤ ç¨. |
|
||||
ëç¨á«¥¨ï ¤«ï ¤ ®£® ¯à¨¬¥à |
|
á ¢ë¢®¤®¬ १ã«ìâ ⮢ |
||||
¢ ᨬ¢®«ì®¬ ( ¥ ⮫쪮 ¢ ç¨á«®¢®¬) ¢¨¤¥ ¬®£ãâ ¡ëâì ¢ë- ¯®«¥ë á ¯®¬®éìî á«¥¤ãî饩 ¯à®£à ¬¬ë ¯ ª¥â MATLAB [82].
198

à®£à ¬¬ ¬®¤¥«¨à®¢ ¨ï ¡«î¤ ⥫ï á®áâ®ï¨ï ¨ ¢®§¬ã饨© ¤«ï ¯® 㥡¥à£¥àã
syms Jx Om
{ ®¯¨á ¨¥ ᨬ¢®«ìëå ¯¥à¥¬¥ëå Jx 0 \
A=[0 1/Jx 0v 0 0 1v 0 0 0]
B=[1/Jx 0 0 ]'v
C=[1 0 0 ]
{ ä®à¬¨à®¢ ¨¥ ᨬ¢®«ìëå ¬ âà¨æ (8.19)\
A =[0 0 0v 1 0 0 v 0 1 0]v
C =[0 0 1]
{ ä®à¬¨à®¢ ¨¥ ¬ âà¨æ ~ ~\
Q=[CvC*AvC*A^2]
A C
Q =[C vC *A vC *A ^2]
{ ¢ëç¨á«¥¨¥ ¬ âà¨æ ¡«î¤ ¥¬®áâ¨\
T=inv(Q )*Qv B =T*B
{ ¢ëç¨á«¥¨¥ ¬ âà¨æë ¯à¥®¡à §®¢ ¨ï ¨ ¬ âà¨æë ~ \
bet1=sqrt(2)*Om bet2=Om^2
T B
{ ®¯à¥¤¥«¥¨¥ § 票© 1 2
P=[1 0 -bet2v 0 1 -bet1v 0 0 1]
{ ä®à¬¨à®¢ ¨¥ ¬ âà¨æë P \
Atil=P*A *inv(P)v Btil=P*B v Abar=Atil(1:2,1:2)
{ ¢ëç¨á«¥¨¥ ¬ âà¨æ \
A A
abar=Atil(1:2,3)v bbar=Btil(1:2,1)
{ ä®à¬¨à®¢ ¨¥ ¬ âà¨æ \ a b
Tbk=inv(T)*inv(P)
{¢ëç¨á«¥¨¥ ¬ âà¨æë Tb jx=54.3v om=0.5
{¢¢®¤ ç¨á«®¢ëå § 票© Jx 0 \
Tb=double(subs(Tbk,[Jx Om],[jx om])) Ao=double(subs(A,Jx,jx)) Bo=double(subs(B,Jx,jx))v
Co=C
{ ¯®¤áâ ®¢ª ç¨á«®¢ëå § 票© ¨ ¯¥à¥¢®¤ ᨬ¢®«ìëå
¬âà¨æ ¢ ç¨á«®¢ë¥\
Af=sym([A zeros(3,2)v abar*C Abar]) Bf=sym([Bv bbar])
199
Cf=Tbk*[0 0 0 1 0v 0 0 0 0 1vC 0 0 ]v
Df=zeros(3,1)v
{ä®à¬¨à®¢ ¨¥ ¢ ᨬ¢®«ì®© ä®à¬¥ ¬ âà¨æ ãà ¢¥¨© á®- áâ®ï¨ï ¥¤¨®© á¨áâ¥¬ë ®¡ê¥ªâ-¬®¤¥«ì-á। - ¡«î¤ ⥫ì\
af=double(subs(Af,[Jx Om],[jx om])) bf=double(subs(Bf,[Jx Om],[jx om])) cf=double(subs(Cf,[Jx Om],[jx om]))v df=Dfv
{¯¥à¥¢®¤ ¬ âà¨æ ¨§ ᨬ¢®«ì®© ¢ ç¨á«®¢ãî ä®à¬ã\ stl=ss(af,bf,cf,df)v
{ä®à¬¨à®¢ ¨¥ á¨á⥬ë,§ ¤ ®© ¢ ä®à¬¥ ãà ¢¥¨© á®- áâ®ï¨ï (á¬. [82])\
t=0:0.1:30v
u=zeros(size(t))'v x0=[0 0.25 5e-3 0 0]'v
{§ ¤ ¨¥ ¨â¥à¢ « ¨ è £ ¬®¤¥«¨à®¢ ¨ï, ¢å®¤®£® ¢®§- ¤¥©áâ¢¨ï ¨ ç «ìëå ãá«®¢¨©\
[y,ti,x]=lsim(stl,u,t,x0)v
plot(ti,x(:,2),ti,y(:,2)),grid,title('M(t)')gure plot(ti,x(:,3),ti,y(:,3)),grid,title('V(t)')
{¬®¤¥«¨à®¢ ¨¥ á¨áâ¥¬ë ¨ ¢ë¢®¤ £à 䨪®¢ ¯à®æ¥áᮢ.
¥§ã«ìâ âë ¬®¤¥«¨à®¢ ¨ï ¯®ª § ë èâà¨å-¯ãªâ¨à®© «¨¨¥© à¨á. 8.3
ëè¥ à áᬮâॠ¯à®æ¥¤ãà á¨â¥§ ¡«î¤ ⥫¥©, ®á®- ¢ ï § ¤ ¨¨ âॡ®¢ ¨© ª ¤¨ ¬¨ª¥ ¯à®æ¥áá ®æ¥¨¢ - ¨ï. áâ® ¯à¨ á¨â¥§¥ á«¥¤ã¥â â ª¦¥ ãç¨âë¢ âì ¢«¨ï¨¥
¥¨§¬¥à塞ëå ¢¥è¨å ¢®§¬ã饨© â®ç®áâì ¯®«ãç ¥¬ëå ®æ¥®ª. ¨â¥§ ¡«î¤ ⥫¥© ¯®«®£® ¯®à浪 , ¯à¨ ª®â®- ஬ ¤®á⨣ ¥âáï ¬¨¨¬¨§ æ¨ï ¤¨á¯¥àᨨ ®è¨¡ª¨ ®æ¥¨¢ ¨ï ¯à¨ á«ãç ©ëå ¢¥è¨å ¢®§¤¥©á⢨ïå (®¯â¨¬ «ìëå 䨫ì- â஢ «¬ { ìîá¨), à áᬮâà¥, ¯à¨¬¥à, ¢ [8, 47, 88].
8.5. ¤ ç¨ ¨ ã¯à ¦¥¨ï
1. гбвм ¤¥©бв¢г¥в ¢®§¬гй¥¨¥, ¨¬¥ой¥¥ ªа®¬¥ «¨¥©®©, £ ମ¨з¥бªго б®бв ¢«пойго б ¥ª®в®а®© з бв®-
⮩ f ¨ ¬¯«¨â㤮© Mf : M(t) = M0 + V t + Mf sin f t: ஬¥ в®£®, ¯гбвм ¯а¨бгвбв¢г¥в ¤¤¨в¨¢ п ¯®£а¥и®бвм ¨§¬¥а¥¨© v(t), ª®â®àãî â ª¦¥ áç¨â ¥¬ £ ମ¨ç¥áª®© á ç áâ®â®© v
200
¨ ¬¯«¨â㤮© v0: à㣨¬¨ á«®¢ ¬¨, â.¥. |
¨§¬¥àï¥¬ë© ¢ë室 |
®¡ê¥ªâ y(t) = !x(t) + v0 sin f t: ©â¨ |
¬¯«¨âã¤ë á®áâ ¢«ï- |
|
^ |
îé¨å ®è¨¡ª¨ ®æ¥¨¢ ¨ï "M (t) = M(t) |
; M(t) (¢ ãáâ ®¢¨¢- |
襬áï ०¨¬¥) ¯® ¢®§¬ãé¥¨ï¬ ¨ è㬠¬ ¨§¬¥à¥¨© |
|
) ¤«ï n-¬¥à®£® ¡«î¤ â¥«ï «¬ (8.20)\ |
|
¡) ¤«ï ¡«î¤ ⥫ï 㥡¥à£¥à (8.21), (8.22).
à ¢¨âì ¯®«ãç¥ë¥ १ã«ìâ âë ¯à¨ ®¤¨ ª®¢ëå § ç¥- ¨ïå ¯ à ¬¥âà 0:
2. á. 42 ¯à¨¢¥¤¥ «¨¥ ਧ®¢ ï ¬®¤¥«ì 㣫®¢®£® ¯à®¤®«ì®£® ¤¢¨¦¥¨ï á ¬®«¥â . ।¯®« £ ï, çâ® ¨§¬¥àï- ¥âáï ⮫쪮 㣮« â £ ¦ #(t), á¨â¥§¨à®¢ âì ¡«î¤ ⥫ì
¯®«®£® ¯®à浪 ¨ ¡«î¤ ⥫ì 㥡¥à£¥à ¤«ï ®æ¥¨¢ - ¨ï ®áâ «ìëå ¯¥à¥¬¥ëå á®áâ®ï¨ï (!z(t) (t)).
3. «ï á¨á⥬ë, § ¤ ®© ¬ âà¨æ ¬¨ [3]
|
2 0 |
1 |
1 3 |
|
2 13 |
|
1 |
0 |
0 |
|||||
|
4 |
1 |
1 |
1 |
5 |
|
4 |
0 |
5 |
|
0 |
0 |
1 |
|
A = |
0 |
1 |
0 |
B = |
1 |
C = |
||||||||
|
|
|
|
|||||||||||
¯®áâநâì ¡«î¤ â¥«ì ¯¥à¢®£® ¯®à浪 .
4. «ï á¨á⥬ë, § ¤ ®© ¬ âà¨æ ¬¨ [3]
|
6 |
0 |
1 |
|
1 |
1 |
7 |
6 |
0 |
7 |
|
1 |
0 |
|
0 |
0 |
1 |
||||
|
A = 2 |
0 |
0 |
1 0 |
3 |
B = 2 |
0 |
3 C = [ 2 0 1 0 ] |
||
|
4 |
0 |
0 |
|
0 |
1 |
5 |
4 |
0 |
5 |
|
|
|
|
|
|
|||||
¯®áâநâì ¡«î¤ ⥫ì á ᮡá⢥묨 § 票ﬨ |
||||||||||
s1 |
= s2 = s3 |
= ;1. |
|
|
|
|
|
|||
|
5. ãáâì S1 |
{ «¨¥© ï á¨á⥬ á ¯®áâ®ï묨 ¯ à ¬¥- |
||||||||
âà ¬¨, ¢å®¤®¬ u(t) ¨ ¢ë室®¬ y(t) [174]). ¨á⥬ S2 ï¥âáï ¡«î¤ ⥫¥¬ á®áâ®ï¨ï ¤«ï á¨á⥬ë S1, ¯®¤ª«îç¥ë¬ ª S1 ¤«¥¦ 騬 ®¡à §®¬.
®ª § âì, çâ® ®¡ê¥¤¨¥ ï á¨á⥬ S = fS1, S2g ¥ã¯à - ¢«ï¥¬ ¯® ¢å®¤ã u(t):
201
