Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления

­â¥à¥á­® à áᬮâà¥âì ¯á¥¢¤®ç áâ®â­ë¥ å à ªâ¥à¨á⨪¨ ¯®«ã祭­ëå â ª¨¬ ᯮᮡ®¬ ¯¥à¥¤ â®ç­ëå ä㭪権 ¤¨áªà¥â- ­ëå á¨á⥬. ª ¨§¢¥áâ­®, í⨠å à ªâ¥à¨á⨪¨ ¯®«ãç îâ-

­®© á¨áâ¥¬ë ¯à¨¡«¨¦¥­­® ¬®£ãâ ¡ëâì ¯®áâ஥­ë ­¥¯®á।- á⢥­­® ¯® ç áâ®â­ë¬ å à ªâ¥à¨á⨪ ¬ ¨á室­®© ­¥¯à¥àë- ¢­®© á¨á⥬ë á ¢¢¥¤¥­¨¥¬ ¤®¯®«­¨â¥«ì­®£® ®âà¨æ ⥫쭮£®

¯® ¢à¥¬¥­¨ ¢ ¤¨áªà¥â­®© á¨á⥬¥ ¨ ¢¬¥á⥠á ⥬ ¨á¯®«ì§®¢ âì å®à®è® à §à ¡®â ­­ë¥ ¯à®æ¥¤ãàë ᨭ⥧ ­¥¯à¥à뢭ëå á¨á- ⥬ ã¯à ¢«¥­¨ï ¤«ï ¯®«ã祭¨ï "­¥¯à¥à뢭ëå ¬®¤¥«¥©" æ¨ä- ஢ëå ॣã«ïâ®à®¢. ®ç­®áâì ¤ ­­®£® ¬¥â®¤ ®¯à¥¤¥«ï¥âáï ᮮ⭮襭¨¥¬ ¬¥¦¤ã ç áâ®â®© á१ !á ­¥¯à¥à뢭®© ¬®¤¥- «¨ (­ ©¤¥­­®© á ãç¥â®¬ 㪠§ ­­®© ¯®¯à ¢ª¨) ¨ ¨­â¥à¢ «®¬

ª¢ ­â®¢ ­¨ï ᨣ­ « ã¯à ¢«¥­¨ï T0: íâ ¯¥ ¯à¥¤¢ à¨â¥«ì- ­®£® ᨭ⥧ ¬®¦­® ४®¬¥­¤®¢ âì ¢ë¯®«­¥­¨¥ ᮮ⭮襭¨ï

¬¨ ­¥¯à¥à뢭®© á¨á⥬ë si ¨ ¥¥ ¤¨áªà¥â­®© ¬®¤¥«¨ zi: ¥©- á⢨⥫쭮, áà ¢­¨¢ ï ä®à¬ã«ë ¤«ï äã­¤ ¬¥­â «ì­ëå á®áâ - ¢«ïîé¨å à¥è¥­¨© ®¤­®à®¤­®£® ¤¨ää¥à¥­æ¨ «ì­®£® ¨ à §­®- áâ­®£® ãà ¢­¥­¨© (yi(t) = P (t)esit ¨ yi[k] = PD[k]zik ᮮ⢥â- á⢥­­®), 12 ã¡¥¦¤ ¥¬áï, çâ® y(kT0) y[k] ¢®§¬®¦­®, ¥á«¨ zi = esiT0 ¯à¨ ¢á¥å i = 1 : : : n: «¥¤®¢ ⥫쭮, ¯¥à¥¤ â®ç- ­ë¥ ä㭪樨 W(s) ¨ WD(z) ¤®«¦­ë ¨¬¥âì 㪠§ ­­ãî á¢ï§ì

12 ¤¥áì P (t) PD[k] { ¬­®£®ç«¥­ë á⥯¥­¥©, ᮮ⢥âáâ¢ãîé¨å ªà â­®- áâï¬ si zi:

152

¬¥¦¤ã ¯®«îá ¬¨ si ¨ zi: «ï ç¨á«¨â¥«¥© ¯¥à¥¤ â®ç­ëå äã­ª- 権 í⮠ᮮ⭮襭¨¥ ­¥ ¢ë¯®«­ï¥âáï. ¤­ ª® ¯à¨ ¤®áâ â®ç­®

6.9.ਢ¥¤¥­¨¥ ãà ¢­¥­¨© ¬­®£®ç áâ®â­ëå ­¥¯à¥àë¢- ­®-¤¨áªà¥â­ëå á¨á⥬ ª ®¤­®ç áâ®â­ë¬ ¬®¤¥«ï¬

­®£¨¥ á¨á⥬ë ã¯à ¢«¥­¨ï ¯à¨¢®¤ ¬¨, ¤¢¨¦ã騬¨áï ®¡ê- ¥ªâ ¬¨, â¥å­®«®£¨ç¥áª¨¬¨ ¯à®æ¥áá ¬¨ ¨ â.¤. ¯®áâ஥­ë á ¯à¨¬¥­¥­¨¥¬ ¬­®£®ç áâ®â­ëå æ¨ä஢ëå ॣã«ïâ®à®¢. ª¨¥ ॣã«ïâ®àë ¨¬¥îâ à §«¨ç­ë¥ ¨­â¥à¢ «ë ¤¨áªà¥â­®á⨠¢ à §-

­ëå ª®­âãà å ã¯à ¢«¥­¨ï. áá«¥¤®¢ ­¨¥ á¨á⥬ á ¬­®£®ç - áâ®â­ë¬¨ ॣã«ïâ®à ¬¨ § âà㤭¥­® ¨§-§ á«®¦­®á⨠¯¥à¥- 室 ª ¥¤¨­®¬ã ¬ ⥬ â¨ç¥áª®¬ã ®¯¨á ­¨î, ¢ ª®â®à®¬ ¡ë á®åà ­ï« áì ᯥæ¨ä¨ª á¨á⥬ë. ªâã «ì­ § ¤ ç ¯®«ãç¥- ­¨ï ¬®¤¥«¨ á¨áâ¥¬ë ¢ ¢¨¤¥ áâ ­¤ àâ­ëå à §­®áâ­ëå ãà ¢- ­¥­¨© á®áâ®ï­¨ï (1.5) ¨«¨ ¯¥à¥¤ â®ç­®© ä㭪樨 WD(z): ¥-

ª®â®àë¥ á¯®á®¡ë à¥è¥­¨ï í⮩ § ¤ ç¨ ¨§«®¦¥­ë ¢ ¤ ­­®¬ ¯ à £à ä¥ [117, 118]. ¤ «ì­¥©è¥¬ ®£à ­¨ç¨¬áï à áᬮ-

çâ® ¨­â¥à¢ «ë ª¢ ­â®¢ ­¨ï Tj (j = 1 2 : : : N £¤¥ N { ç¨- á«® à §«¨ç­ëå ¯¥à¨®¤®¢ ¤¨áªà¥â­®áâ¨) â ª®¢ë çâ® á।¨ ­¨å

1

¢¢¥á⨠­ ¨¬¥­ìèãî ç áâ®âã ª¢ ­â®¢ ­¨ï f0 = T : «¥¥ à á-

ᬮâਬ § ¤ çã ¯®«ã祭¨ï ãà ¢­¥­¨© á®áâ®ï­¨ï0 ¨ ¯¥à¥¤ - â®ç­ëå ä㭪権 ¬®¤¥«¨, ¯®«ã祭­®© ¯à¨¢¥¤¥­¨¥¬ ãà ¢­¥­¨© á¨áâ¥¬ë ª ¯¥à¨®¤ã T0 â ¬®¤¥«ì ¤®«¦­ ãç¨âë¢ âì ­ «¨ç¨¥ ª®­âã஢ ॣ㫨஢ ­¨ï, ¢ ª®â®àëå ¯à®¨á室¨â ¯à¥®¡à §®- ¢ ­¨¥ ᨣ­ « á ¡®«ì訬¨ ç áâ®â ¬¨ fj = cj f0:

6.9.1. ¥â®¤ ­ «¨â¨ç¥áª¨å ¯à¥®¡à §®¢ ­¨©

áᬮâਬ á­ ç « ­¥¯à¥à뢭ãî á¨á⥬ã, § ¤ ­­ãî ãà ¢- ­¥­¨ï¬¨ á®áâ®ï­¨ï

¯®áâ®ï­­®¥ ­ ¨­â¥à¢ « å ¤«¨â¥«ì­®á⨠T1 ¢å®¤­®¥ ¢®§¤¥©á- ⢨¥. à ¢­¥­¨ï § ¬ª­ã⮩ á¨á⥬ë á ãç¥â®¬ ®¡à â­®© á¢ï§¨ ¨¬¥îâ ¢¨¤

x1(t) = ;A + BK x1(t) + Bg1(tk1) y1(t) = Cx1(t): (6.42)

«ï ­ ©¤¥­­®© á¨áâ¥¬ë ¢ë¯®«­¨¬ ¯¥à¥å®¤ ª ¤¨áªà¥â­®© ¬®- ¤¥«¨ ®â­®á¨â¥«ì­® ¬®¬¥­â®¢ tk1 ¯® ®¯¨á ­­®© ¢ ¯. 6.4.2. ¯à®- 楤ãà¥. ®«ã稬 à §­®áâ­ë¥ ãà ¢­¥­¨ï:

x1[k1 + 1] = P1x1[k1] + Q1g1[k1 ] y1 [k1] = Cx1[k1] (6.43)

á® ¢å®¤­ë¬ ¢®§¤¥©á⢨¥¬ g2: ¯à¥¤¥«¨¬ ®¡é¨© ¢¥ªâ®à á®áâ®-

ï­¨ï x[k1] = colfx1 [k1] x01[k1 ]g: ª ­¥âà㤭® ã¡¥¤¨âìáï, ãà ¢- ­¥­¨ï (6.43), (6.44) ¬®¦­® ®¡ê¥¤¨­¨âì ¢ ®¤­® ãà ¢­¥­¨¥:

¤«ï ­¥ª®â®à®£® ¯®áâ®ï­­®£® ­ âãà «ì­®£® d: «¥¤®¢ ⥫쭮,

¢ â¥ç¥­¨¥ ª ¦¤ëå d ¨­â¥à¢ «®¢ ¤«¨â¥«ì­®á⨠T1 (®âáç¨âë¢ ï

­¨ï, ®¯à¥¤¥«ïî騥 ¯®¢¥¤¥­¨¥ à áᬮâ७­®© ­¥¯à¥à뢭®-

¢ ª®â®à®© ¬ âà¨æë P Q C ¨¬¥îâ ¡«®ç­ãî áâàãªâãàã:

ª¨¬ ®¡à §®¬, ­ ©¤¥­ë ãà ¢­¥­¨ï á®áâ®ï­¨ï ¤¨áªà¥â­®© á¨á⥬ë á ­ ¨¡®«ì訬 ¯¥à¨®¤®¬ ¤¨áªà¥â­®á⨠T0: à®æ¥áá ¯à¥®¡à §®¢ ­¨ï ¬ âà¨æ ¬®¦­® ¯à®¤®«¦¨âì, ¥á«¨ ¨¬¥îâáï ¤à㣨¥ ¤¨áªà¥â­ë¥ ¯®¤á¨á⥬ë á ¨­â¥à¢ « ¬¨ ª¢ ­â®¢ ­¨ï, ªà â­ë¬¨ T0: ®«ã祭­ë¥ ãà ¢­¥­¨ï ¬®¦­® ¨á¯®«ì§®¢ âì

¤«ï ­ 宦¤¥­¨ï ¯¥à¥¤ â®ç­®© ä㪭樨 á¨á⥬ë (6.48), ®¯à¥- ¤¥«¥­¨ï ç áâ®â­ëå å à ªâ¥à¨á⨪ ¨ ¨áá«¥¤®¢ ­¨ï ¥¥ ãá⮩- 稢®áâ¨.

6.9.2. ¥â®¤ ¬®¤¥«¨à®¢ ­¨ï

§« £ ¥¬ë© §¤¥áì ¬¥â®¤ à¥è¥­¨ï ¯®áâ ¢«¥­­®© § ¤ ç¨ á¢®- ¤¨âáï ª ¯à¨¢¥¤¥­¨î ¬®¤¥«¨ á¨áâ¥¬ë ª ¢¨¤ã (6.14) ¯ã⥬ à á- ç¥â ¯¥à¥å®¤­®© ä㭪樨. «ï ¯à®áâëå § ¤ ç à¥è¥­¨¥ ¬®- ¦¥â ¡ëâì ¯®«ã祭® ­ «¨â¨ç¥áª¨, ®¤­ ª®, ª ª ¯à ¢¨«®, ¯à¨- 室¨âáï ¯à¨¡¥£ âì ª ç¨á«¥­­®¬ã ¨­â¥£à¨à®¢ ­¨î. ।« - £ ¥¬ë© ­¨¦¥ ¯®¤å®¤ ¯®ª §ë¢ ¥â ¢®§¬®¦­®áâì ¨á¯®«ì§®¢ ­¨ï ¯à®£à ¬¬ ¬®¤¥«¨à®¢ ­¨ï ¤«ï ¯®«ã祭¨ï ¥¤¨­®£® ®¯¨á ­¨ï

­¥¯à¥à뢭®-¤¨áªà¥â­ëå á¨á⥬. ­ ç «ì­ë¥ â®çª¨ ®âáç¥- ⠯ਬ¥¬ ¬®¬¥­âë ¢à¥¬¥­¨ tk = kT0 k = 0 1 : : : ¨ à áᬮ- âਬ ¯à®¬¥¦ã⪨ [tk tk+1]: ç¨âë¢ ï áâ 樮­ à­®áâì á¨áâ¥- ¬ë, ¤«ï íâ¨å ¯à®¬¥¦ã⪮¢ ¬®¦­® ¯à¨­ïâì tk = 0 ¨ ¢ ¤ «ì- ­¥©è¥¬ à áᬠâਢ âì ¯à®¬¥¦ã⮪ [0 T0 ]: 뤥«¨¬ ¢­ãâਠ­¥£® ¬®¬¥­âë ¢à¥¬¥­¨ tjr (j = 1 2 : : : N r = 1 2 : : : dj ), ¢ ª®â®àë¥ ¨§¬¥­ï¥âáï á®áâ®ï­¨¥ j-© ¤¨áªà¥â­®© ¯®¤á¨á⥬ë.­¨ ®¡à §ãîâ ¯®á«¥¤®¢ ⥫쭮á⨠tjr = tj0 + rTj £¤¥ tj0 Tj { "­ ç «ì­ë¥ ä §ë" ¤«ï ª ¦¤®© ¯®¤á¨á⥬ë. ãé¥á⢥­­® â®, çâ® ¤«ï ¢á¥å k ¢¨¤ íâ¨å ¯®á«¥¤®¢ ⥫쭮á⥩ ®¤¨­ ª®¢ ¢ ᨫ㠯®áâ®ï­á⢠Tj ¨ ªà â­®á⨠ç áâ®â ª¢ ­â®¢ ­¨ï. «¥- ¤®¢ ⥫쭮, ®¯¥à â®à S ¢ ãà ¢­¥­¨¨ á®áâ®ï­¨¥-¢å®¤-¢ë室

á¨á⥬ë y(t) = S(x(t0 )\ u[t0 t]) áâ 樮­ à­ë©. ஬¥ ⮣®, ®­ ¡ã¤¥â ¨ «¨­¥©­ë¬ ¢á«¥¤á⢨¥ «¨­¥©­®á⨠ª ¦¤®© ¯®¤á¨áâ¥- ¬ë. ®áª®«ìªã ­ á ¨­â¥à¥áãîâ ãà ¢­¥­¨ï á¨áâ¥¬ë ®â­®á¨- ⥫쭮 ¬®¬¥­â®¢ kT0 ¡ã¤¥¬ ¤®¯®«­¨â¥«ì­® ¯à¥¤¯®« £ âì, çâ® §­ 祭¨ï u(tk) ®¤­®§­ ç­® ®¯à¥¤¥«ïîâ ¢¨¤ u(t) ¢­ãâਠª ¦¤®- £® ¯à®¬¥¦ã⪠[tk tk+1] (á¬. ¢ëè¥ 6.4.2. 6.7.). ®í⮬㠮⭮-

á¨â¥«ì­® ¬®¬¥­â®¢ tk à áᬠâਢ ¥¬ ï á¨á⥬ ¬®¦¥â ¡ëâì 156

®¯¨á ­ à §­®áâ­ë¬¨ ãà ¢­¥­¨ï¬¨ á®áâ®ï­¨ï

x[k + 1] = P x[k] + Qu[k] y[k] = Cx[k] + Du[k] k = 0 1 : : : (6:.49)

¯à¥¤¥«¨¢ §­ 祭¨ï ¬ âà¨æ P Q C D ¬ë ¯®«ã稬 à¥è¥­¨¥ ¯®áâ ¢«¥­­®© § ¤ ç¨. «ï í⮣® ãç⥬, çâ® à¥è¥­¨¥ à §­®áâ- ­®£® ãà ¢­¥­¨ï (6.49) ¯® ­ «®£¨¨ á (6.8) ¨¬¥¥â ¢¨¤

ª¨¬ ®¡à §®¬, ¤«ï ¯®«ã祭¨ï P ¬®¦­® n à § ¯à®¬®¤¥«¨-

B = [x1 [1].x2[1]. : : : .xm[1]]: ëç¨á«¥­¨¥ xi [1] ¢ë¯®«­ï¥âáï ¬®- ¤¥«¨à®¢ ­¨¥¬ á¨áâ¥¬ë ¯à¨ ­ã«¥¢ëå ­ ç «ì­ëå ãá«®¢¨ïå ¨ ¥¤¨­¨ç­ëå ¢å®¤ å 横«¨ç¥áª¨ ¤«ï i = 1 2 : : : m : ëç¨á«¥-

­¨¥ ¬ âà¨æë C ¯à®¨§¢®¤¨âáï ¯® á⮫¡æ ¬ C = [y1.y2 .: : : .yn ] yi { ¢ë室 á¨áâ¥¬ë ¯à¨ u = 0 xi = ei i = 1 2 : : : m k = 0:«ï ®¯à¥¤¥«¥­¨ï ¬ âà¨æë D á«¥¤ã¥â ¯®«ãç¨âì ¢ë室 ¯à¨ x = 0 ui = ei i = 1 2 : : : m k = 0: ¬¥â¨¬, çâ® ¤«ï ¢ëç¨- á«¥­¨ï ¬ âà¨æ C D ­¥ âॡã¥âáï ¬®¤¥«¨à®¢ âì á¨á⥬㠭 㪠§ ­­®¬ ¨­â¥à¢ «¥. ⨠¬ âà¨æë ­ 室ïâáï ¯® «£¥¡à ¨-

ç¥áª¨¬ ᮮ⭮襭¨ï¬ ¯à¨ ¯®áâ®ï­­®¬ á®áâ®ï­¨¨ ¨ ¢å®¤¥ á¨- á⥬ë. áᬮâਬ á«¥¤ãî騩 ¯à¨¬¥à.

ਬ¥à. ãáâì ­¥¯à¥à뢭®-¤¨áªà¥â­ ï á¨á⥬ ®¯¨áë¢ - ¥âáï á«¥¤ãî騬¨ ¤¨ää¥à¥­æ¨ «ì­®-à §­®áâ­ë¬¨ ãà ¢­¥­¨- ﬨ:

x1[k1 + 1] = K1T1u1 (k1T1) + x1[k1]

157

{ ­ ¨¡®«ì訩 ¯¥à¨®¤ ¤¨áªà¥â­®á⨠á¨á⥬ë. ਠ㪠§ ­­ëå ¯à¥¤¯®«®¦¥­¨ïå ¬¥â®¤ ­¥ ¨¬¥¥â «£®à¨â¬¨ç¥áª®© ®è¨¡ª¨ ¨ ¥£® â®ç­®áâì ®¯à¥¤¥«ï¥âáï ¯®£à¥è­®áâìî ¬®¤¥«¨à®¢ ­¨ï.­ 祭¨¥ í⮩ ¯®£à¥è­®á⨠¬®¦¥â ¡ëâì 㬥­ì襭® ¯®¤å®¤ï- 騬 ¢ë¡®à®¬ ¬¥â®¤ ¬®¤¥«¨à®¢ ­¨ï (ç¨á«¥­­®£® ¨­â¥£à¨- ஢ ­¨ï) ¨ á­¨¦¥­¨¥¬ ¢¥«¨ç¨­ë ¥£® è £ . ¯¨á ­­ë© §¤¥áì

¬¥â®¤ ¬®¦­® ¨á¯®«ì§®¢ âì ¨ ¤«ï ¯®áâ஥­¨ï ¤¨áªà¥â­ëå ¬®- ¤¥«¥© à áᬮâ७­ëå ¢ëè¥ ®¤­®ç áâ®â­ëå á¨á⥬. ਠí⮬ ­¥ âॡã¥âáï ¯à¥®¡à §®¢ë¢ âì ãà ¢­¥­¨ï á¨áâ¥¬ë ª ¥¤¨­ë¬ ãà ¢­¥­¨ï¬ á®áâ®ï­¨ï (6.13), ¤®áâ â®ç­® à ᯮ« £ âì ¯à®- £à ¬¬®© ¬®¤¥«¨à®¢ ­¨ï á¨á⥬ë. ­­ë© ¬¥â®¤ ¬®¦­® â ª- ¦¥ ¨á¯®«ì§®¢ âì ¤«ï ¯à¨¡«¨¦¥­­®£® ¨áá«¥¤®¢ ­¨ï ­¥áâ æ¨- ®­ à­ëå ¨ ­¥«¨­¥©­ëå á¨á⥬.

158

6.10.á⮩稢®áâì ¤¨áªà¥â­ëå ¬®¤¥«¥©. ¢ï§ì á ¬¥â®- ¤ ¬¨ ç¨á«¥­­®£® ¨­â¥£à¨à®¢ ­¨ï

ਠ¯®áâ஥­¨¨ ¤¨áªà¥â­ëå ¬®¤¥«¥© ­¥¯à¥à뢭ëå á¨á⥬

¥áâ¥á⢥­­® ¢®§­¨ª ¥â âॡ®¢ ­¨¥ á®åà ­¥­¨ï ᢮©á⢠ãá⮩- 稢®áâ¨: ãá⮩稢 ï ­¥¯à¥à뢭 ï á¨á⥬ ¤®«¦­ ¯à¨¢®- ¤¨âì ª ãá⮩稢®© ¤¨áªà¥â­®© ¬®¤¥«¨, ¢ á«ãç ¥ ­¥ãá⮩- 稢®á⨠¨á室­®© á¨áâ¥¬ë ¨ ¤¨áªà¥â­ ï ¬®¤¥«ì ⮦¥ ¤®«¦- ­ ¯®«ãç¨âìáï ­¥ãá⮩稢®©. ª ¯®ª § ­® ­¨¦¥, ¤«ï â®ç­ëå ¬¥â®¤®¢ ¯¥à¥å®¤ íâ® âॡ®¢ ­¨¥ ¢ë¯®«­¥­®. ਡ«¨¦¥­­ë¥

¬¥â®¤ë ¤ ­­®¬ã ãá«®¢¨î ®â¢¥ç îâ ¤ «¥ª® ­¥ ¢á¥£¤ . ¨¦¥ ¯à¨¢¥¤¥­ë १ã«ìâ âë ¨áá«¥¤®¢ ­¨ï ãá«®¢¨© ãá⮩稢®á⨠¯® ®â­®è¥­¨î ª à áᬮâ७­ë¬ ¯à¨¡«¨¦¥­­ë¬ ä®à¬ã« ¬ ¨ ¤ ­ ¨­â¥à¯à¥â æ¨ï ¯®«ã祭­ëå १ã«ìâ ⮢ ¤«ï § ¤ ç¨ ç¨- á«¥­­®£® ¨­â¥£à¨à®¢ ­¨ï ¤¨ää¥à¥­æ¨ «ì­ëå ãà ¢­¥­¨©.

6.10.1. á«®¢¨ï ãá⮩稢®áâ¨

®ç­ë© ¯¥à¥å®¤. ª ¨§¢¥áâ­®, ᨬ¯â®â¨ç¥áª ï ãá⮩- 稢®áâì ­¥¯à¥à뢭ëå á¨á⥬ ¨¬¥¥â ¬¥áâ®, ¥á«¨ ª®à­¨ å à ª- â¥à¨áâ¨ç¥áª®£® ¬­®£®ç«¥­ (ᮡá⢥­­ë¥ ç¨á« ) ¬ âà¨æë A

â¨ç¥áª¨, ¥á«¨ ¢ë¯®«­¥­® ãá«®¢¨¥: jzij < 1 ¯à¨ det(zi In ; P ) = 0 i = 1 : : : n: «ï ¯à®¢¥àª¨ ãá⮩稢®á⨠¤¨áªà¥â­®© ¬®¤¥-

«¨, ¯®«ã祭­®© ­ ®á­®¢¥ ­¥ª®â®à®£® ¬¥â®¤ , ¢®á¯®«ì§ã¥¬áï á«¥¤ãî饩 ¨§¢¥áâ­®© ¨§ ⥮ਨ ¬ âà¨æ ⥮६®©. [53]

¥®à¥¬ . ᫨ äã­ªæ¨ï f(s) ®¯à¥¤¥«¥­ ­ ᯥªâॠn n-¬ âà¨æë A ⮠ᮡá⢥­­ë¥ ç¨á« zi n n-¬ âà¨æë

P =f(A) ¢ëà ¦ îâáï ä®à¬ã« ¬¨ zi = f (si) i = 1 : : : n: 2®£« á­® â®ç­®© ä®à¬ã«¥ (6.17), P = eAT0: ®í⮬ã ᮡ- á⢥­­ë¥ ç¨á« zi ¬ âà¨æë P ®¯а¥¤¥«повбп б®®в­®и¥­¨¥¬

(6.13), (6.14) íª¢¨¢ «¥­â­ë. áᬮâਬ ⥯¥àì ®¯¨á ­­ë¥ ¢ ¯. 6.5.2. ¯à¨¡«¨¦¥­­ë¥ ¬¥â®¤ë.

2. ¥â®¤ ©«¥à . ®£« á­® í⮬㠬¥â®¤ã, ¯® (6.20) ¯®- «ãç ¥¬ P = In +AT0: «¥¤®¢ ⥫쭮, zi = 1 + siT0, i = 1 : : : n :஢¥àª ãá«®¢¨ï ãá⮩稢®á⨠jzij < 1 ¯à¨¢®¤¨â ª ­¥à ¢¥­-

159

á⢠¬

( i+1)2 + i2 < 1 i = T0 Resi i = T0 Imsi i = 1 : : : n : (6.53)

á«®¢¨¥ (6.53) ®§­ ç ¥â, çâ® §­ 祭¨ï ª®à­¥© å à ªâ¥à¨- áâ¨ç¥áª®£® ¬­®£®ç«¥­ á¨á⥬ë, 㬭®¦¥­­ë¥ ­ ¨­â¥à¢ « ª¢ ­â®¢ ­¨ï, ¤®«¦­ë ­ 室¨âìáï ­ ª®¬¯«¥ªá­®© ¯«®áª®á⨠¢­ãâਠ®ªà㦭®á⨠¥¤¨­¨ç­®£® à ¤¨ãá á 業â஬ ¢ â®çª¥ (;1 |0): ­® íª¢¨¢ «¥­â­® ­¥à ¢¥­áâ¢ã

áâ®ï­­®© ¢à¥¬¥­¨, ¯®«ã祭­ ï ¯® ä®à¬ã«¥ ©«¥à , ¡ã¤¥â ­¥- ãá⮩稢®© ¯à¨ T0=2 > T. ¨áªà¥â­ ï ¬®¤¥«ì ª®­á¥à¢ ⨢- ­®£® §¢¥­ (s1 2 = | ) ­¥ãá⮩稢 ¯à¨ ¢á¥å T0 > 0: 13 ⮠᢮©á⢮ áãé¥á⢥­­® á㦠¥â ®¡« áâì ¯à¨¬¥­¥­¨ï ®£® ¬¥-

⮤ ©«¥à , ®£à ­¨ç¨¢ ï ¥¥ ¬ «ë¬¨ (®â­®á¨â¥«ì­® ¬®¤ã«¥©

á«®¢¨¥ (6.55) ®§­ ç ¥â, çâ® ª®à­¨ å à ªâ¥à¨áâ¨ç¥áª®£® ¬­®- £®ç«¥­ á¨á⥬ë, 㬭®¦¥­­ë¥ ­ ¨­â¥à¢ « ª¢ ­â®¢ ­¨ï, ¤®«¦-

¡®© ãá⮩稢®© ­¥¯à¥à뢭®© á¨áâ¥¬ë ¡ã¤¥â ¯®«ã祭 ãá⮩- 稢 ï ¤¨áªà¥â­ ï ¬®¤¥«ì ¯à¨ ¢á¥å ( ­¥ ⮫쪮 ¬ «ëå) T0 > 0:⬥⨬, ç⮠᢮©á⢠ãá⮩稢®á⨠­¥¯à¥à뢭ëå ¨ ¤¨á- ªà¥â­ëå ¬®¤¥«¥© ­¥ ¡ã¤ãâ íª¢¨¢ «¥­â­ë¬¨: ãáâ®©ç¨¢ë¥ ¤¨á-

ªà¥â­ë¥ ¬®¤¥«¨ ¬®£ãâ ¯®«ãç¨âìáï ¨ ¯à¨ ­¥ãá⮩稢®á⨠¨á- 室­ëå ­¥¯à¥à뢭ëå á¨á⥬. ஬¥ ⮣®, â®ç­®áâì ¯¯à®ªá¨- ¬ 樨 ¯® í⮬㠬¥â®¤ã ­¥¢¥«¨ª (ª ª ®â¬¥ç¥­® ¢ëè¥, ®è¨¡ª

13 ¯à ¢¥¤«¨¢® â ª¦¥ ¨ â®, çâ® ¯à¨ T0 ! 0 §­ 祭¨ï zi ¯®«ã祭­ë¥ ¯® ¢á¥¬ 㪠§ ­­ë¬ ¬¥â®¤ ¬, áâ६ïâáï ª â®ç­ë¬ ¢¥«¨ç¨­ ¬ zi = esiT0:

160

¨¬¥¥â ¯®à冷ª ¬ «®á⨠O(T0 ) ): ãç訥 १ã«ìâ âë ¯®«ãç - îâáï á ¯®¬®éìî "¤¨ £®­ «ì­ëå" ¯¯à®ªá¨¬ 権 ¤¥.

4. ¯¯à®ªá¨¬ 樨 ¤¥ ¯à¨ = . ®¦­® ãáâ ­®-

権 (6.24) (¬¥â®¤ á⨭ ) ¨ (6.25). ç¨âë¢ ï, çâ® ¨å ®è¨¡ª¨ ¨¬¥îâ ¯®à浪¨ ¬ «®á⨠O(T03 ) ¨ O(T05) ᮮ⢥âá⢥­­®, ¬®¦- ­® à ááç¨âë¢ âì ­ ¯®«ã祭¨¥ ¤¨áªà¥â­ëå ¬®¤¥«¥©, ᢮©á⢠ª®â®àëå ¤®áâ â®ç­® ¡«¨§ª¨ ª ᢮©á⢠¬ ¨á室­ëå ­¥¯à¥àë¢- ­ëå á¨á⥬.

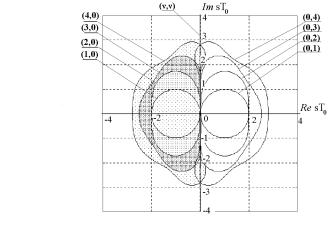
ª ç¥á⢥ ¨««îáâà 樨 ­ à¨á. 6.1 ¯®ª § ­ë £à ­¨- æë ®¡« á⥩ ãá⮩稢®á⨠¤¨áªà¥â­ëå ¬®¤¥«¥© ­¥¯à¥à뢭ëå

á¨á⥬ ¢ ¯«®áª®á⨠sT0. «¥¤ã¥â ãç¥áâì, çâ® ¤«ï ­¥ï¢­ëå ¬¥- ⮤®¢ ( 6= 0) ®¡« áâì ãá⮩稢®á⨠à ᯮ« £ ¥âáï ¯® ¢­¥è- ­îî áâ®à®­ã ®â £à ­¨æë.

¨á. 6.1. ¡« á⨠ãá⮩稢®á⨠¤¨áªà¥â­ëå ¬®¤¥«¥© ¤«ï ­¥ª®â®àëå ¯¯à®ªá¨¬ 権 ¤¥.

6.10.2. á⮩稢®áâì ¬¥â®¤®¢ ç¨á«¥­­®£® ¨­â¥£à¨à®¢ ­¨ï

®¦­® ãáâ ­®¢¨âì â¥á­ãî á¢ï§ì ¬¥¦¤ã à áᬮâ७­ë¬¨ ¢ë- è¥ ¬¥â®¤ ¬¨ ¯®áâ஥­¨ï ¤¨áªà¥â­ëå ¬®¤¥«¥© ­¥¯à¥à뢭ëå

161