Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления

¬ , ¥á«¨ ¨¬¥¥âáï ¢§ ¨¬­®-®¤­®§­ ç­®¥ ᮮ⢥âá⢨¥ ¬¥¦¤ã ¯¥à¥¬¥­­ë¬¨ ¢å®¤-¢ë室 ¨ á®áâ®ï­¨¥¬ ®¡ê¥ªâ . â® á®®â- ¢¥âá⢨¥ ¨¬¥¥âáï ¤«ï ¯®«­®áâìî ­ ¡«î¤ ¥¬ëå ®¡ê¥ªâ®¢. 1á¨á⥬ å ã¯à ¢«¥­¨ï ­ ¨¡®«¥¥ à á¯à®áâà ­¥­ë ®æ¥­ª¨ ⨯ "䨫ìâà æ¨ï". ਠ⠪¨å ®æ¥­ª å ⥬¯ ®æ¥­¨¢ ­¨ï ᮢ- ¯ ¤ ¥â á ⥬¯®¬ ¯®«ã祭¨ï ¨­ä®à¬ 樨, çâ® áãé¥á⢥­­® ¤«ï ¯®áâ஥­¨ï á¨á⥬ ॠ«ì­®£® ¢à¥¬¥­¨. ¨¦¥ ¡ã¤¥â à áᬠ- âਢ âìáï ¨¬¥­­® § ¤ ç 䨫ìâà 樨 ¯à¨¬¥­¨â¥«ì­® ª «¨-

­¥©­ë¬ ®¡ê¥ªâ ¬ ã¯à ¢«¥­¨ï.

áᬮâਬ ¬®¤¥«ì ®¡ê¥ªâ ¢ ¢¨¤¥ ãà ¢­¥­¨© á®áâ®ï­¨ï:

- ¢å®¤­®© ¨ ¢ë室­®© ¢¥ªâ®àë\ A(t) B(t) C(t) { ¨§¢¥áâ­ë¥ ¬ -

âà¨ç­ë¥ ä㭪樨. ¡ê¥ªâ ¯®¤¢¥à¦¥­ ¤¥©áâ¢¨î ¢®§¬ã饭¨© f (t) ¨ "è㬠(¯®£à¥è­®áâ¨) ¨§¬¥à¥­¨©" v(t): ç¨â ¥âáï, çâ® ¯à¨ à ¡®â¥ á¨áâ¥¬ë ¤®áâã¯­ë ¨§¬¥à¥­¨î ¯à®æ¥ááë u(t) y(t)

x(t) f (t) v(t) { ­¥¤®áâ㯭ë. áᬠâਢ ¥âáï § ¤ ç ¯®- «ã祭¨ï ®æ¥­ª¨ á®áâ®ï­¨ï ®¡ê¥ªâ x^(t). à®æ¥áá x^(t) ¯®«ã- 祭­ë© á ¯®¬®éìî ­¥ª®â®à®£® «£®à¨â¬ , ¤®«¦¥­ ¢ ®¯à¥¤¥-

«ãç¨âì ᨬ¯â®â¨ç¥áª¨ â®ç­ãî ®æ¥­ªã á®áâ®ï­¨ï á «î¡ë¬ § ¤ ­­ë¬ ¢à¥¬¥­¥¬ ¯¥à¥å®¤­®£® ¯à®æ¥áá . 2 «¨ï­¨¥ ¢®§- ¬ã饭¨© ¨ è㬮¢ ¨§¬¥à¥­¨ï ¯à¨¢®¤¨â ª ¯®ï¢«¥­¨î ®è¨¡®ª ®æ¥­¨¢ ­¨ï. ¥ª®â®àë© ­ «¨§ í⮣® ¢«¨ï­¨ï ¡ã¤¥â ¤ ­ ¢ á«¥¤ãî饬 ¯ à £à ä¥.

1 ஬¥ в®£®, ¯а¥¤¯®« £ ¥вбп, зв® ¨¬¥¥вбп ¤®бв в®з­® ¯®«­ п ¯а¨®а- ­ п ¨­д®а¬ ж¨п ®¡ ®¡к¥ªв¥ ¢ ¢¨¤¥ ¥£® ¬ в¥¬ в¨з¥бª®© ¬®¤¥«¨ ¨ ¯ а ¬¥- ва®¢. ¤ з¨ б ­¥¯®«­®© ¯а¨®а­®© ¨­д®а¬ ж¨¥© ®в­®бпвбп ª ¤ ¯â¨¢- ­ë¬. ¢¥¤¥­¨ï ® ¬¥â®¤ å ¨å à¥è¥­¨ï ¬®¦­® ¯®«ãç¨âì ¨§ ¯. 12.3. (á. 307)

¤­­®© ª­¨£¨, ¨§ ª­¨£¨ [64], â ª¦¥ ¨§ à ¡®â [8, 23, 76, 93, 103, 106, 191]. 2 ®«¥¥ ⮣®, ¯®«­ ï ­ ¡«î¤ ¥¬®áâì ⥮à¥â¨ç¥áª¨ ¯®§¢®«ï¥â ¯®áâà®-

¨âì «£®à¨â¬ ®æ¥­¨¢ ­¨ï, ®¡« ¤ î騩 ª®­¥ç­ë¬ ¢à¥¬¥­¥¬ á室¨¬®á⨠®æ¥­®ª á®áâ®ï­¨ï. ¤­ ª® ॠ«¨§ æ¨ï â ª®£® «£®à¨â¬ § âà㤭¥­ ¨§-§ ¢«¨ï­¨ï ¯ à ¬¥âà¨ç¥áª¨å ¨ ª®®à¤¨­ â­ëå ¢®§¬ã饭¨©, â ª¦¥ á«®¦­®- á⥩ ¢ëç¨á«¨â¥«ì­®£® å à ªâ¥à .

182

¬ ¥ ç ­ ¨ ¥ . à ¢­¥­¨ï (8.1) ᮮ⢥âáâ¢ãîâ á¨á⥬¥ ­¥¯à¥à뢭®£® ¢à¥¬¥­¨. ¤ ç ®æ¥­¨¢ ­¨ï à áᬠâਢ ¥âáï â ª¦¥ ¤«ï ¤¨áªà¥â­ëå á¨á⥬, ¯®í⮬㠭¨¦¥ ­ àï¤ã á (8.1) ¡ã¤ã⠨ᯮ«ì§®¢ ­ë à §­®áâ­ë¥ ãà ¢­¥­¨ï

x[k + 1] = A[k]x[k] + B[k]u[k] + f[k]

y[k] = C[k]x[k] + v[k] x[t0] = x0 k = k0 k0 + 1 : : : (8.2)

¨áªà¥â­ë© «£®à¨â¬ ®æ¥­¨¢ ­¨ï § ¤ ¥âáï à §­®áâ­ë¬ ãà ¢- ­¥­¨¥¬ ¨ á«ã¦¨â ¤«ï ¯®«ã祭¨ï ®æ¥­ª¨ á®áâ®ï­¨ï x^[k]:

8.2. ¡«î¤ ⥫¨ á®áâ®ï­¨ï

¡«î¤ ⥫ì á®áâ®ï­¨ï (¨¤¥­â¨ä¨ª â®à á®áâ®ï­¨ï, ­ ¡«î¤ - î饥 ãáâனá⢮, ­ ¡«î¤ ⥫ì) ¬®¦­® ¯à¥¤áâ ¢¨âì ¢ ¢¨¤¥

¬®¤¥«¨ ®¡ê¥ªâ ã¯à ¢«¥­¨ï, ­ ¢å®¤ ª®â®à®© ¯®áâ㯠¥â â® ¦¥ ã¯à ¢«ïî饥 ¢®§¤¥©á⢨¥, çâ® ¨ ­ ®¡ê¥ªâ ã¯à ¢«¥­¨ï

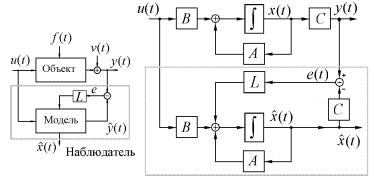
¨, ªà®¬¥ ⮣®, ¤®¯®«­¨â¥«ì­ë© ᨣ­ « ª®à४樨 (®¡à â­®© á¢ï§¨). â®â ᨣ­ « ¯®«ãç ¥âáï ¨§ ­¥¢ï§ª¨ ¬¥¦¤ã ¢ë室 ¬¨ ®¡ê¥ªâ ¨ ¬®¤¥«¨ (à¨á. 8.1).

¨á. 8.1. ਭ樯 ¯®áâ஥­¨ï ¨ áâàãªâãà­ ï á奬 ­ ¡«î- ¤ ⥫ï.

£® ¢«¨ï­¨¥ ¯à¨¤ ¥â ¯®¢¥¤¥­¨î ¬®¤¥«¨ ª ç¥á⢥­­® ­®- ¢ë¥ ᢮©á⢠(®â«¨ç­ë¥ ®â ᢮©á⢠®¡ê¥ªâ ). ®¡á⢥­­ë¥

¤¢¨¦¥­¨ï ¬®¤¥«¨ ¨ ®¡ê¥ªâ ®ª §ë¢ îâáï à §«¨ç­ë¬¨, ­® ¯¥- ६¥­­ë¥ á®áâ®ï­¨ï ¬®¤¥«¨ á«ã¦ ⠮業ª ¬¨ á®áâ®ï­¨ï ®¡ê-

183

¥ªâ . «ï á¨á⥬ ­¥¯à¥à뢭®£® ¢à¥¬¥­¨ ­ ¡«î¤ â¥«ì ®¯¨áë- ¢ ¥âáï ãà ¢­¥­¨¥¬

{ n l-¬ âà¨æ ª®íää¨æ¨¥­â®¢ ®¡à â­®© á¢ï§¨ ¯® ­¥¢ï§ª¥ ¬¥- ¦¤ã ¢ë室 ¬¨ ®¡ê¥ªâ ¨ ­ ¡«î¤ ⥫ï. ¨­â¥§ ­ ¡«î¤ â¥«ï § ª«îç ¥âáï ¢ ¢ë¡®à¥ ¬ âà¨æë L(t):

⬥⨬, çâ® ¬ë à áᬠâਢ ¥¬ ­ ¡«î¤ ⥫ì, ã ª®â®à®£® à §¬¥à­®áâì ¢¥ªâ®à á®áâ®ï­¨ï â ª ï ¦¥, ª ª ¨ ã ®¡ê¥ªâ (â ª ­ §ë¢ ¥¬ë© ­ ¡«î¤ â¥«ì ¯®«­®£® ¯®à浪 , ¨«¨ ­ ¡«î¤ ⥫쫬 ­ ). ¤­ ª® íâ® ãá«®¢¨¥ ­¥®¡ï§ ⥫쭮: ¢áâà¥ç îâáï ­ ¡«î¤ ⥫¨ ª ª ¯®­¨¦¥­­®£® ¯®à浪 (á¬. ­¨¦¥ "­ ¡«î¤ - ⥫ì 㥭¡¥à£¥à "), â ª ¨ ¯®¢ë襭­®£® ¯®à浪 ( ¤ ¯â¨¢­ë¥ ­ ¡«î¤ ⥫¨, á¬. ¯. 12.6.5.).

«ï ¨áá«¥¤®¢ ­¨ï à ¡®âë ­ ¡«î¤ ⥫ï à áᬮâਬ ®è¨¡-

ªã ®æ¥­¨¢ ­¨ï "(t) = (x(t) ; x^(t)): ëç¨â ï ¨§ (8.1) ãà ¢­¥­¨¥ (8.3), ¯®«ãç ¥¬ ãà ¢­¥­¨¥ ¤«ï ®è¨¡ª¨

ª ¢¨¤­® ¨§ í⮣® ãà ¢­¥­¨ï, ¨áâ®ç­¨ª ¬¨ ®è¨¡ª¨ "(t) ï-

¨­ ¬¨ª ¯¥à¥å®¤­®£® ¯à®æ¥áá ¢ â ª¨å á¨á⥬ å ®¯à¥¤¥«ï-

饭¨ï f (t) ¨ èã¬ë v(t) ®вбгвбв¢гов, в® ¯а®ж¥бб ®ж¥­¨¢ ­¨п б¨¬¯в®в¨з¥бª¨ гбв®©з¨¢ ¨ "(t) ! 0 ¯à¨ t ! 1 ¤«ï «î¡ëå ­ ç «ì­ëå §­ 祭¨© x0 x^0: âà¨æ A­ § ¢¨á¨â ®â ¯ à ¬¥- â஢ ®¡ê¥ªâ ã¯à ¢«¥­¨ï (¬ âà¨æ A C ¢ (8.1)) ¨ ¬ âà¨æë L

3 ¬¥­­® áâ 樮­ à­ë¥ á¨áâ¥¬ë ¨ ¡ã¤ãâ à áᬮâà¥­ë ¢ ­ áâ®ï饩 £« ¢¥. ¢¥¤¥­¨ï ® ­¥áâ 樮­ à­ëå «£®à¨â¬ å ®æ¥­¨¢ ­¨ï ¯à¨¢¥¤¥­ë, ­ ¯à¨¬¥à, ¢ [3, 47].

184

¢ë¡®à ª®â®à®© ®¯à¥¤¥«ï¥âáï ¯à®¥ªâ¨à®¢é¨ª®¬. ª á«¥¤ã¥â ¨§ ¯à¨¢¥¤¥­­ëå ¢ëè¥ ¢ ¯. 7.3. ªà¨â¥à¨¥¢, ¤«ï ¯®«­®áâìî ­ ¡- «î¤ ¥¬®£® ®¡ê¥ªâ ¢á¥£¤ ¨¬¥¥âáï â ª ï ¬ âà¨æ L ç⮠ᮡ- á⢥­­ë¥ ç¨á« ¬ âà¨æë A­ ¡ã¤ãâ § ¤ ­­ë¬¨. «¥¤®¢ ⥫ì- ­®, ¢ë¡®à®¬ L ¬®¦­® ®¡¥á¯¥ç¨âì âॡ㥬®¥ ¡ëáâத¥©á⢨¥ ¯à®æ¥áá ®æ¥­¨¢ ­¨ï. 4 а¨ ®вбгвбв¢¨¨ б¨£­ « ª®аа¥ªж¨¨ (L = 0) ¤¨­ ¬¨ª ¯à®æ¥áá ®æ¥­¨¢ ­¨ï ¯®«­®áâìî ®¯à¥¤¥«ï- ¥âáï ¤¨­ ¬¨ª®© ®¡ê¥ªâ . ç áâ­®áâ¨, ¤«ï ­¥ãá⮩稢ëå ¨ ­¥©âà «ì­®-ãá⮩稢ëå ®¡ê¥ªâ®¢ ᨬ¯â®â¨ç¥áª®¥ ®æ¥­¨¢ -

¢­¥è­¨å ¢®§¤¥©á⢨ïå. ª ¢¨¤­® ¨§ (8.4), íâ® ¢«¨ï­¨¥ ®ª - §ë¢ ¥âáï à §­ë¬ ¯® ®â­®è¥­¨î ª ¢®§¬ã饭¨ï¬ f (t) á ®¤­®© áâ®à®­ë, ¨ ¯®¬¥å ¬ ¨§¬¥à¥­¨© v(t) { á ¤à㣮©. ®í⮬㠯ਠ®¯à¥¤¥«¥­¨¨ L á«¥¤ã¥â ãç¨âë¢ âì å à ªâ¥à¨á⨪¨ ¢­¥è­¨å ¢®§¤¥©á⢨© ¨ ®¡¥á¯¥ç¨¢ âì ª®¬¯à®¬¨áá ¬¥¦¤ã âॡ®¢ ­¨ï- ¬¨ ¡ëáâத¥©áâ¢¨ï ¨ â®ç­®á⨠á¨á⥬ë. ¡ëç­® ¯®¢ë襭¨¥ ¡ëáâத¥©á⢨ï á¢ï§ ­® á 㢥«¨ç¥­¨¥¬ í«¥¬¥­â®¢ ¬ âà¨æë L ¨, á«¥¤®¢ ⥫쭮, á ¯®¤ ¢«¥­¨¥¬ ¢«¨ï­¨ï ¢®§¬ã饭¨© ¨ ¯®¤- ç¥àª¨¢ ­¨¥¬ ¤¥©áâ¢¨ï ¯®¬¥å ¨§¬¥à¥­¨ï. «ï ¡®«¥¥ ¤¥â «ì-

­®£® ­ «¨§ ¬®¦­® ¨á¯®«ì§®¢ âì ¯¥à¥¤ â®ç­ë¥ ä㭪樨 ¯® ®è¨¡ª¥ ®â ¢®§¬ã饭¨© Wf"(s) ¨ ¯®¬¥å Wv"(s) ®¯à¥¤¥«ï¥¬ë¥ ä®à¬ã« ¬¨

Wf"(s) = (sIn ; A + LC);1 Wv"(s) = ; (sIn ; A + LC);1 L:

¯â¨¬ «ì­ë© (¢ á¬ëá«¥ ¬¨­¨¬ã¬ ¤¨á¯¥àᨨ jj"(t)jj) ¢ë¡®à ¬ âà¨æë L ¯à¨ ¤¥©á⢨¨ á«ãç ©­ëå ¢®§¬ã饭¨© ¨ ¯®¬¥å ¯à¨- ¢®¤¨â ª ®¯â¨¬ «ì­®¬ã 䨫ìâàã «¬ ­ - ìîᨠ[47].

áᬮâਬ ®¯à¥¤¥«¥­¨¥ L ¨§ ãá«®¢¨© ¡ëáâத¥©á⢨ï.

à ªâ¥à¨áâ¨ç¥áª¨© ¬­®£®ç«¥­ ­ ¡«î¤ â¥«ï ¯à¥¤áâ ¢¨¬

¢¢¨¤¥

det(sIn ; A­) det(sIn ; A + LC) = sn + 1sn;1 + + n: (8.5)

®íää¨æ¨¥­âë i § ¢¨áï⠮⠯ à ¬¥â஢ ®¡ê¥ªâ ¨ ¬ âà¨- æë L: à¨à ¢­¨¢ ï ¨å ª § ¤ ­­ë¬ §­ 祭¨ï¬, ¯®«ãç ¥¬ á¨- á⥬ã n «¨­¥©­ëå «£¥¡à ¨ç¥áª¨å ãà ¢­¥­¨© ®â­®á¨â¥«ì­®

4 «¥¤ã¥â, ¯à ¢¤ , ®â¬¥â¨âì, çâ® ¢¥«¨ç¨­ ¯¥à¥à¥£ã«¨à®¢ ­¨ï "(t) ¬®- ¦¥â ®ª § âìáï §­ ç¨â¥«ì­®©. à¥¬ï ¯¥à¥å®¤­®£® ¯à®æ¥áá å à ªâ¥à¨§ã¥â ᪮à®áâì § âãå ­¨ï ¢¥«¨ç¨­ë ®â­®á¨â¥«ì­®© ®è¨¡ª¨.

185

¨áª®¬ëå n l í«¥¬¥­â®¢ ¬ âà¨æë L: ਠ¯®«­®© ­ ¡«î¤ - ¥¬®á⨠®¡ê¥ªâ ¤ ­­ ï á¨á⥬ ¨¬¥¥â à¥è¥­¨¥ ¤«ï «î¡ëå A C i (¯à¨ l = 1 íâ® à¥è¥­¨¥ ¥¤¨­á⢥­­®). ᫨ ¨§- ¬¥à¥­¨î ¤®áâ㯭® ­¥áª®«ìª® ¢ë室­ëå ¯¥à¥¬¥­­ëå (l > 1) â® ¬ âà¨æ L ®¯à¥¤¥«ï¥âáï ­¥®¤­®§­ ç­®. «¥¤®¢ ⥫쭮, ¯à¨ ¢ë¡®à¥ L ¬®¦­® ãç¥áâì ¤®¯®«­¨â¥«ì­ë¥ âॡ®¢ ­¨ï ¯® ®è¨¡ª ¬ ®â ¢­¥è­¨å ¢®§¤¥©á⢨© ¨ ᮮ⢥âá⢥­­® ¯¥à¥à á- ¯à¥¤¥«¨âì ª®íää¨æ¨¥­âë ¯¥à¥¤ ç¨. ¥è¥­¨¥ § ¤ ç¨ á¨­â¥§ ¬®¦­® ¢ë¯®«­ïâì «£¥¡à ¨ç¥áª¨¬¨ ¬¥â®¤ ¬¨ á ¨á¯®«ì§®¢ -

­¨¥¬ á¯¥æ¨ «ì­ëå ª ­®­¨ç¥áª¨å ä®à¬ ãà ¢­¥­¨© á®áâ®ï­¨ï (á¬., ­ ¯à¨¬¥à, [3]). «ï ®¯à¥¤¥«¥­¨ï ¦¥« ¥¬ëå ª®íää¨æ¨- ¥­â®¢ å à ªâ¥à¨áâ¨ç¥áª®£® ¬­®£®ç«¥­ (8.5) ४®¬¥­¤ã¥âáï ¨á¯®«ì§®¢ âì áâ ­¤ àâ­ë¥ ä®à¬ë, ­ ¯à¨¬¥à ¡¨­®¬¨ «ì­ãî ä®à¬ã, ¨«¨ ä®à¬ã ââ¥à¢®àâ : [47, 76]

áâ 樮­ à­®¬ á«ãç ¥ ¥£® ¤¨­ ¬¨ª ®¯à¥¤¥«ï¥âáï å à ªâ¥- à¨áâ¨ç¥áª¨¬ ¬­®£®ç«¥­®¬ det(zIn ; A­) det(zIn ; A + LC) ª®à­¨ zi ª®â®à®£® ¨§ ãá«®¢¨ï ãá⮩稢®á⨠¤®«¦­ë ¡ëâì ¯®

¬®¤ã«î ¬¥­ìè¥ ¥¤¨­¨æë. ¢®©á⢠¤¨áªà¥â­®£® ­ ¡«î¤ â¥- «ï ¨ ¯à®æ¥¤ãà ᨭ⥧ ­ «®£¨ç­ë ¨§«®¦¥­­ë¬ ¢ëè¥ ¤«ï ­¥¯à¥à뢭®£® á«ãç ï. ¬¥â¨¬, çâ® ¤«ï (8.6) ¬ âà¨æ L ¬®- ¦¥â ¡ëâì ¢ë¡à ­ ¨§ ãá«®¢¨ï zi = 0 i = 1 2 : : : n çâ® ¤ ¥â ª®­¥ç­®¥ ¢à¥¬ï ¯¥à¥å®¤­®£® ¯à®æ¥áá ®æ¥­¨¢ ­¨ï, ­¥ ¯à¥¢ë-

è î饥 nT0 £¤¥ n { ¯®à冷ª á¨á⥬ë, T0 { ¨­â¥à¢ « ª¢ ­â®- ¢ ­¨ï. 5

ª ®â¬¥ç¥­® ¢ëè¥, ¤«ï ¯®áâ஥­¨ï á¨á⥬ ®æ¥­¨¢ ­¨ï, ®¡« ¤ îé¨å § ¤ ­­ë¬¨ ¤¨­ ¬¨ç¥áª¨¬¨ ᢮©á⢠¬¨, âॡã- ¥âáï ¯®«­ ï ­ ¡«î¤ ¥¬®áâì ®¡ê¥ªâ ã¯à ¢«¥­¨ï. ᫨ ¤«ï

5 ®ç­¥¥ £®¢®àï, ¯¥à¥å®¤­ë© ¯à®æ¥áá § ¢¥àè ¥âáï ­¥ ¡®«¥¥, 祬 § n è £®¢, çâ® ¢ á¨á⥬ å ॠ«ì­®£® ¢à¥¬¥­¨ á ¯®áâ®ï­­ë¬ ¯¥à¨®¤®¬ ª¢ ­- ⮢ ­¨ï T0 ᮮ⢥âáâ¢ã¥â 㪠§ ­­®¬ã ¢à¥¬¥­­®¬ã ¨­â¥à¢ «ã.

186

®¡ê¥ªâ í⮠᢮©á⢮ ­¥ ¢ë¯®«­ï¥âáï, ­® ®­ ï¥âáï ®¡­ - à㦨¢ ¥¬ë¬ (á¬. ®¯à¥¤¥«¥­¨¥ 8 ¢ ¯. 7.1.) â® ãá⮩稢®áâì ¯à®æ¥áá ®æ¥­¨¢ ­¨ï ¬®¦¥â ¡ëâì ®¡¥á¯¥ç¥­ , ®¤­ ª® ­¥«ì§ï ¯®«ãç¨âì ¯à®¨§¢®«ì­®¥ § ¤ ­­®¥ à ᯮ«®¦¥­¨¥ ª®à­¥© ¬­®- £®ç«¥­ (8.5).

8.3. ¡«î¤ ⥫¨ ¯®­¨¦¥­­®£® ¯®à浪

á®áâ®ï­¨ï ª®â®àëå ᮢ¯ ¤ ¥â á ¯®à浪®¬ ãà ¢­¥­¨© ®¡ê¥ªâ ¨ à ¢­ n: ®¦­® г¬¥­ми¨вм ¯®а冷ª ­ ¡«о¤ в¥«п, ¨б¯®«м- §гп ­¥¯®ба¥¤бв¢¥­­® ᮤ¥а¦ йгобп ¢ ¢л室­ле ¯¥а¥¬¥­­ле

¨­ä®à¬ æ¨î ® á®áâ®ï­¨¨ ®¡ê¥ªâ . â® ¤ ¥â ¢®§¬®¦­®áâì ¯®- áâநâì «£®à¨â¬ ®æ¥­¨¢ ­¨ï ¯®à浪 n ; p £¤¥ p = rank C (®¡ëç­® p = l:) ª¨¥ ¨¤¥­â¨ä¨ª â®àë á®áâ®ï­¨ï ­ §ë¢ îâ-

áï ­ ¡«î¤ ⥫ﬨ ¯®­¨¦¥­­®£® ¯®à浪 , ¨«¨ ­ ¡«î¤ ⥫ﬨ㥭¡¥à£¥à [3, 174].

áᬮâਬ áâ 樮­ à­ë© ¯®«­®áâìî ­ ¡«î¤ ¥¬ë© ®¡ê- ¥ªâ, ãà ¢­¥­¨ï ª®â®à®£® ¨¬¥îâ ¢¨¤

§ í⮩ á¨áâ¥¬ë ¬®¦­® ¢ë¤¥«¨âì ¯®¤á¨á⥬㠯®à浪 n ; p á ¨§¢¥áâ­ë¬¨ (¤®áâ㯭묨 ¨§¬¥à¥­¨î) ¢å®¤ ¬¨ u(t) y(t):®«¥¥ ⮣®, ¤«ï í⮩ ¯®¤á¨áâ¥¬ë ¢á¥£¤ ¬®¦­® ®¡¥á¯¥ç¨âì § ¤ ­­ë¥ ª®íää¨æ¨¥­âë å à ªâ¥à¨áâ¨ç¥áª®£® ¬­®£®ç«¥­ .

«ï í⮣® 㬭®¦¨¬ ¢â®à®¥ ãà ¢­¥­¨¥ ¢ (8.8) ­ ¯à®¨§¢®«ì- ­ãî (n ; p) p-¬ âà¨æã E ¨ á«®¦¨¬ ¯®«ã祭­®¥ ¢ëà ¦¥­¨¥ á ¯¥à¢ë¬ ãà ¢­¥­¨¥¬. ®«ã稬

w(t);Ey(t) = (A11 ;EA21 )w(t)+(A12 ;EA22)y(t)+(B1 +EB2)u(t):

â® ¢ëà ¦¥­¨¥ ¬®¦­® ¯¥à¥¯¨á âì ¢ ¢¨¤¥

w(t) ; Ey(t) = (A11 ; EA21);w(t) ; Ey(t) + +(A11E ; EA21E+ A12 ; EA22)y(t) + (B1 ; EB2 )u(t):

¤¥áì v(t) { ­¥¨§¬¥àï¥¬ë© ¢¥ªâ®à á®áâ®ï­¨ï, ¢ â® ¢à¥¬ï ª ª u(t) y(t) ¨§¬¥аповбп. ¢¥¤¥¬ ­ ¡«о¤ в¥«м, га ¢­¥­¨¥ ª®в®-

ª ¨ ¢ëè¥, ¢ëç¨â ï (8.9) ¨§ (8.10), ­ ©¤¥¬ ãà ¢­¥­¨¥ ¤«ï ®è¨¡ª¨ ®æ¥­¨¢ ­¨ï v^(t) ; v(t) :

v^(t) ; v(t) = ;A11 ; EA21;v^(t) ; v(t) :

§ ¯®«ã祭­®£® ãà ¢­¥­¨ï á«¥¤ã¥â, çâ® v^(t) ; v(t) ! 0, ¯à¨- 祬 ¤¨­ ¬¨ª ®è¨¡ª¨ ®¯à¥¤¥«ï¥âáï ᮡá⢥­­ë¬¨ ç¨á« ¬¨

¬âà¨æë A11 ; EA21:

®«ã稢 ®æ¥­ªã ¢¥ªâ®à v(t) ­¥âà㤭® ¯¥à¥©â¨ ª ®æ¥­ª¥

¢á¥£® ¢¥ªâ®à á®áâ®ï­¨ï ª ª ¢ ª ­®­¨ç¥áª®¬ (8.8), â ª ¨ ¢ ¨á- 室­®¬ ¡ §¨á¥. 業ª¨ w^(t), y^(t) ¢¥ªâ®à x(t) ¯®«ãç îâáï ¢ ¢¨¤¥

w^(t) = v^(t) + Ey(t) y^(t) = y(t):

¡à â­ë¬ ¯à¥®¡à §®¢ ­¨¥¬ á ¬ âà¨æ¥© T;1 ¯®«ãç ¥¬ ®æ¥­ªã x^(t) ¢¥ªâ®à á®áâ®ï­¨ï á¨á⥬ë (8.7).

188

ç¥á⢮ ¯®«ã祭­®© ®æ¥­ª¨ á®áâ®ï­¨ï ¢ §­ ç¨â¥«ì­®© á⥯¥­¨ ®¯à¥¤¥«ï¥âáï ¬ âà¨æ¥© A11 ; EA21: ®¦­® ¯®ª § âì (á¬. § ¤ çã ¯. 11 ­ á. 180), çâ® ¥á«¨ ¨á室­ ï á¨á⥬ (8.8)

¯®«­®áâìî ­ ¡«î¤ ¥¬ , â® í⨬ ¦¥ ᢮©á⢮¬ ®¡« ¤ ¥â ¨ ¯ à (A11 A21 ). «¥¤®¢ ⥫쭮, ¬®£ãâ ¡ëâì ®¡¥á¯¥ç¥­ë ¯à®- ¨§¢®«ì­® § ¤ ­­ë¥ §­ 祭¨ï ª®íää¨æ¨¥­â®¢ å à ªâ¥à¨áâ¨ç¥- ᪮£® ¬­®£®ç«¥­ ­ ¡«î¤ â¥«ï ¯ã⥬ ¯®¤å®¤ï饣® ¢ë¡®à ¬ âà¨æë E:

«ï ¨««îáâà 樨 à áᬮâਬ á«¥¤ãî騩 ¯à¨¬¥à.

« ­á¨à®¢ª áâ¥à¦­ï. áᬮâਬ § ¤ çã áâ ¡¨«¨- § 樨 áâ¥à¦­ï ¢ ¢¥à⨪ «ì­®¬ ¯®«®¦¥­¨¨ ([174]). 6 ãáâì áâ¥à¦¥­ì ¨¬¥¥â ¤«¨­ã l ¨ ¢áï ¬ áá á®á।®â®ç¥­ ­ ¥£® ¢¥àå­¥¬ ª®­æ¥ (â.¥. à áᬠâਢ ¥âáï ®¡à 饭­ë© ¬ ⥬ â¨- ç¥áª¨© ¬ ïâ­¨ª). à ¢­¥­¨¥ ¤¨­ ¬¨ª¨ áâ¥à¦­ï ®â­®á¨â¥«ì- ­® 㣫 ®âª«®­¥­¨ï ®â ¢¥à⨪ «¨ '(t), ᮣ« á­® § ª®­ã ìî- â®­ , ¨¬¥¥â ¢¨¤

£¤¥ g 9:81 { ã᪮७¨¥ ᢮¡®¤­®£® ¯ ¤¥­¨ï\ u(t) { ã¯à ¢«ï- î饥 ¢®§¤¥©á⢨¥ { £®à¨§®­â «ì­®¥ ¯¥à¥¬¥é¥­¨¥ ®á­®¢ ­¨ï áâ¥à¦­ï (à¨á. 8.2). ஬¥ ⮣®, ¢ë¯®«­¥­® £¥®¬¥âà¨ç¥áª®¥ ᮮ⭮襭¨¥

믮«­ïï «¨­¥ ਧ æ¨î ®â­®á¨â¥«ì­® ¢¥à⨪ «ì­®£® á®áâ®- ï­¨ï à ¢­®¢¥á¨ï, ¯à¨¢¥¤¥¬ ãà ¢­¥­¨ï (8.11), (8.12) ®â­®á¨- ⥫쭮 x(t) ª ¢¨¤ã

x(t) = gl ;x(t) ; u(t) :

¢¥¤¥¬ £®à¨§®­â «ì­ãî ᪮à®áâì ¯¥à¥¬¥é¥­¨ï v(t) = x(t):âáî¤ ¯®«ã稬 ãà ¢­¥­¨ï á®áâ®ï­¨ï á¨á⥬ë

6 â § ¤ ç ¬®¦¥â à áᬠâਢ âìáï, ª ª ã¯à®é¥­­ë© ¢ ਠ­â § ¤ - ç¨ ã¯à ¢«¥­¨ï ®¡à 饭­ë¬ ¬ ïâ­¨ª®¬ ­ ⥫¥¦ª¥ (á¬. á. 30) ¨ á«ã¦¨âì ¯à¨¡«¨¦¥­¨¥¬ ª â ª¨¬ á«®¦­ë¬ § ¤ ç ¬ ã¯à ¢«¥­¨ï, ª ª áâ ¡¨«¨§ æ¨ï 㣫®¢®£® ¯®«®¦¥­¨ï à ª¥âë-­®á¨â¥«ï [19], ®¡¥á¯¥ç¥­¨¥ ¤¢¨¦¥­¨ï á¯ãâ­¨- ª ¯® § ¤ ­­®© âà ¥ªâ®à¨¨, ã¯à ¢«¥­¨ï á ¬®«¥â®¬ [23, 19, 98], ¢¥à⮫¥â®¬ ¨ â ª ¤ «¥¥.

189

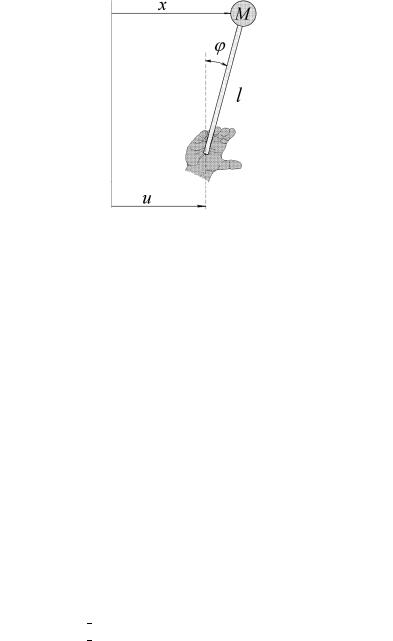
¨á. 8.2. « ­á¨à®¢ª áâ¥à¦­ï.

âà¨æ ã¯à ¢«ï¥¬®áâ¨ à ¢­

£¤¥ y(t) { ¨§¬¥àï¥¬ë© ¢ë室 ®¡ê¥ªâ . âà¨æ ­ ¡«î¤ ¥¬®-

áâìî ­ ¡«î¤ ¥¬®© (á«¥¤®¢ ⥫쭮 { ­¥¢ë஦¤¥­­®©). ¤¥­-

â¨ä¨ª â®à ¯®«­®£® ¯®à浪 (8.3) ¤«ï ­¥¥ ¡ã¤¥â ®¯¨áë¢ âìáï ãà ¢­¥­¨ï¬¨

¤¥áì l1 l2 { ¯ à ¬¥âàë ­ ¡«î¤ ⥫ï, ¢ë¡®à ª®â®àëå ¢ë- ¯®«­ï¥âáï ¯® § ¤ ­­ë¬ §­ 祭¨ï¬ ª®íää¨æ¨¥­â®¢ å à ªâ¥- à¨áâ¨ç¥áª®£® ¬­®£®ç«¥­ det(sI ; A­) = s2 + l2s + g(l1 ; 1)l;1:

190

¤¥­â¨ä¨ª â®à (8.13) ¨á¯®«ì§ã¥â ¨§¬¥à¥­¨ï u(t) x(t) ¤«ï ¯®- «ã祭¨ï ®æ¥­®ª v^(t) x^(t): ᫨ ­¥ áâ ¢¨âì § ¤ çã 䨫ìâà - 樨 è㬮¢ ¨§¬¥à¥­¨©, â® ¢â®à ï ®æ¥­ª ï¥âáï «¨è­¥© ¨ ¬®¦­® 㬥­ìè¨âì ¯®à冷ª «£®à¨â¬ ®æ¥­¨¢ ­¨ï, ¨á¯®«ì§ãï

­¡«î¤ ⥫ì 㥭¡¥à£¥à (8.10).

¬¥â¨¬, çâ® ¢ à áᬠâਢ ¥¬®¬ ¯à¨¬¥à¥ ãà ¢­¥­¨ï ®¡ê- ¥ªâ 㦥 ¨¬¥îâ âॡ㥬ãî ª ­®­¨ç¥áªãî ä®à¬ã (8.8) ¨ ¯à¥-

âà¨æë (᪠«ïà­ë¥ ª®íää¨æ¨¥­âë) A11 = A22 = 0 A21 = 1 A12 = gl;1 B1 = ;gl;1 ¯®í⮬ã (8.10) ¯à¨­¨¬ ¥â ¢¨¤

v^(t) = ;ev^(t) + (gl;1 ; e2)x(t) ; gl;1u(t):

¤¥áì e { ¯®¤«¥¦ 騩 ¢ë¡®àã ¯ à ¬¥âà ­ ¡«î¤ ⥫ï. ®- «ã稬 å à ªâ¥à¨áâ¨ç¥áª¨© ¬­®£®ç«¥­

(n ; 1)-¬¥à­ëå ­ ¡«î¤ ⥫¥© ¤«ï á¨á⥬ ᮠ᪠«ïà­ë¬ ¢ë- 室®¬ (â®ç­¥¥, ¯à¨ rank C = 1).

«£®à¨â¬ á®á⮨⠨§ á«¥¤ãîé¨å è £®¢.

1. à ¢­¥­¨ï á®áâ®ï­¨ï á¨á⥬ë (¬ âà¨æë A B C) ­¥- ¢ë஦¤¥­­ë¬ ¯à¥®¡à §®¢ ­¨¥¬ ¯à¨¢®¤¨¬ ª ¢¨¤ã (á¬.