1.6. Опір провідника. Питомий опір. Провідність. Питома провідність

Під час впорядкованого руху носії зарядів багаторазово стикаються з іншими частинками речовини, які є в тепловому русі. Ці зіткнення частково затримують впорядкований рух носіїв зарядів і є причиною опору провідного середовища проходженню струму.

Властивість середовища, що характеризує його здатність проводити електричний струм, називають питомою провідністю γ. Питома провідність γ залежить від фізичних властивостей провідного матеріалу й від температури. У системі СІ [γ ] = 1 Ом ^-1м ^-1 = 1 См/м.

В класичній електронній теорії величина γ визначається такою форму­лою:

(1.32)

де n₀ – кількість електронів в 1 см³ об'єму металу (n₀ 10²² 10²³ см^-3); e = –1,602∙10^-19 Кл – абсолютне значення заряду електрона; – середня довжи­на вільного пробігу (λ 10^-8 см); – середня (арифметична) швидкість тепло­вого руху електронів при певній температурі (при t = + 20 °С, 10⁵см/с); m – маса молекули.

Із (1.32) наочно видно, якими величинами визначається електропровід­ність речовини.

Величина

(1.33)

називається питомим опором провідника. Розмірність питомого опору [ ] = 1Oм∙мм²/м чи 1Oм∙м, похідна одиниця 1 Ом∙см.

Зі зміною температури провідника γ, як і , змінюються. Залежність пи­томого опору провідника від температури виражається залежністю:

(1.34)

де – питомий опір провідника при 0 °С; t – температура в градусах Цельсія; α – температурний коефіцієнт опору.

Р

Рис. 1.17. До визначення опору провідника

озглянемо однорідний провідник, дов­жина якого l, з незмінним поперечним пере­різом S, до кінців якого прикладена напруга u (рис. 1.17). В провіднику протікає струм і. Вектори будуть збігатися з довжиною провідника .

Залежність між густиною струму в даній точці провідного середовища й напруженістю поля виражається залежністю (1.28) яку ще називають законом Ома в диференціальній формі. Ця залежність справедлива для областей поза джерелами ЕРС.

Згідно з (1.9) 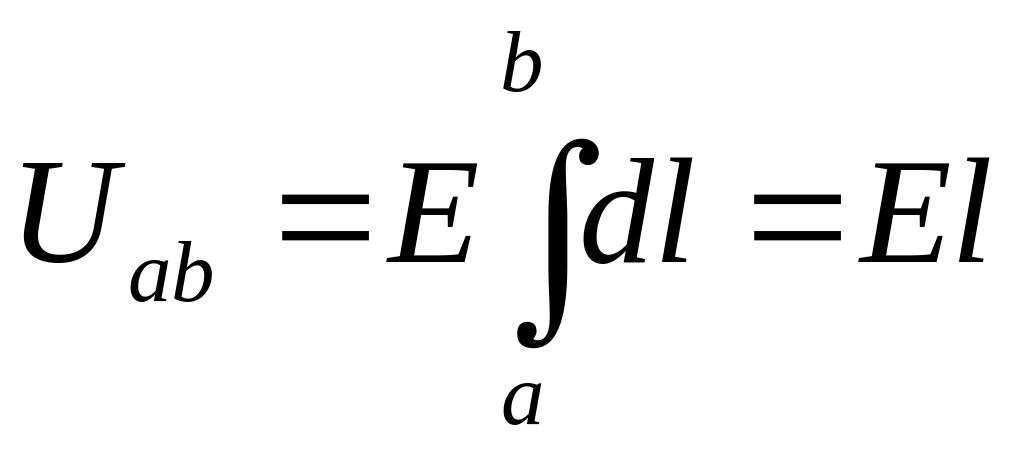і ураховуючи, що та , одержимо:

(1.35)

В (1.35), величина – це опір провідника завдовжки , площею пере­різу S, виготовленого з матеріалу питомою провідністю γ. Отже, маємо:

(1.36)

Рівність (1.35) тепер запишеться так:

(1.37)

що є законом Ома для ділянки кола, з опором r. Розмірність r: ; похідні одиниці: кілоом – (1 кОм = 10³ Ом) і мегаОм (1 МОм = 10⁶ Oм).

Розмірності величин, які входять у формулу (1.36), такі:

[r]=1Oм, [l]=1м, [S]=1мм², ,

Я

Рис. 1.18. До визначення питомого опору провідника

кщо взяти провідник певного матеріалу завдовжки l = 1 м, перерізом S = 1 мм², то опір та­кого провідника, згідно з (1.36), буде дорівнювати питомому опорові ρ (рис. 1.19). У довідковій літературі наводяться дані опорів металевих провідників для l=1м, S=1мм², t = +20 °С. Ці опори дорівнюють їхнім ρ в розмірності і температурі +20 °С.

Опір металевих провідників із підвищенням температури зростає. Ця зміна визначається таким співвідношенням:

(1.38)

де t₁, t₂ – початкова та кінцева температури, °С; r₁, r₂ – опори при темпера­турах t₁, t₂, Ом; α –температурний коефіцієнт опору, 1/°С.

Для чистих металів α 0,004 °С^-1, що означає збільшення їх опору на 4 % при підвищенні температури на 10 °С. Ряд сплавів, таких, як манганін, констан­тан, мають великий питомий опір і дуже малий температурний коефіцієнт опору. Ці сплави застосовують для виготовлення резисторів зі сталим (майже не залежним від температури) значенням опору. Від'ємний температурний коефіцієнт опору мають вугілля та електроліти, для котрих α  – 0,02 на 1 °С.

Величину, обернену до опору, називають провідністю:

(1.39)

Одиниця вимірювання провідності, обернена до одиниці опору, називається сіменс (См): [g] = 1 / Ом = См.

В табл. 1.2 наведені значення ρ, γ і α деяких провідникових матеріалів.

Таблиця 1.2