2. Електрична ємність

2.1. Електрична ємність тіл

Нехай маємо відокремлене нерухоме провідне тіло, заряджене до потен­ціалу φ, яке оточує діелектрик проникністю ε, що не залежить від напруженості поля, тобто в кожній точці середовища є сталою величиною. Тоді заряд такого тіла пропорційний його потенціалу:

чи

(2.1)

Величина С називається електричною ємністю тіла.

Отже, електрична ємність відокремленого тіла дорівнює відношенню за­ряду тіла до його потенціалу.

Оскільки значення потенціалу прийнято нульовим на поверхні землі, то φ у (2.1) дорівнює напрузі між землею і заданим відокремленим тілом (рис. 2.1): U = φ – φ₃ = φ –0 = = φ. Отже, співвідношення (2.1) можна записати ще так:

(2.2)

Р

Рис. 2.1. Відок­ремлене провід­не тіло зарядом q, оточене діе­лектриком про­никністю ε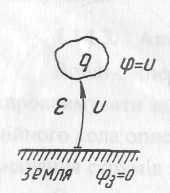

озподіл заряду на поверхні відокремленого тіла й картина електричного поля навколо нього залежать від форми тіла. Отже, і потенціал U, і ємність С залежать теж від форми тіла, якщо задана величина заряду q. Якщо тіло оточене одно­рідним діелектриком електричною проникністю ε, то напру­женість електричного поля Ε і, відповідно, потенціал U, при заданому заряді зворотно пропорційні ε діелектрика, що випливає із теореми Гаусса (1.2). На основі цього маємо:

(2.3)

де g₁, g_2­… – геометричні величини, які характеризують форму й розміри тіла.

Д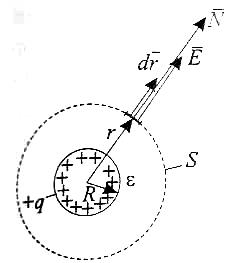 ля прикладу визначимо ємність відокремленої кулі радіуса R. Згідно з теоремою Гаусса напруженість електричного поля відокремленого точкового заряду (1.3) . Використаємо цю рівність для одержання потенціалу відокремленого тіла, зарядже­ного зарядом "+q" (рис. 2.2). Будемо вважати, що r » R, тоді заряд "+q" можемо вважати точковим. Тут R – радіус кулі, в центрі якої, вважаємо, знаходиться точковий заряд "+q".

Із визначення (1.14) потенціал на поверхні зарядженої кулі радіуса R дорівнює:

Рис. 2.2. Відокремлена провідна куля радіуса R в діелектрику проник­ністю ε

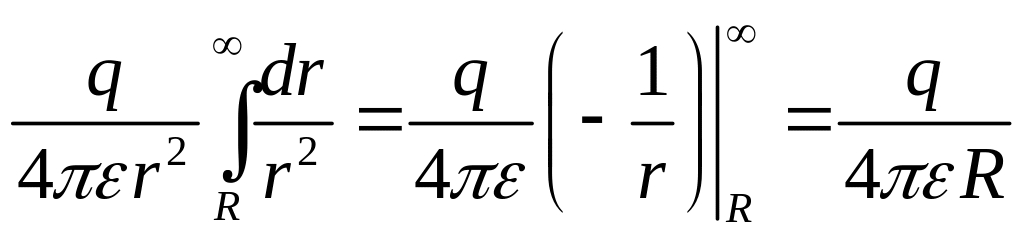, тут кут =0°.

Тоді ємність відокремленої кулі радіуса R визначиться як:

і остаточно C = 4πεR, що підтверджує співвідношення (2.3).

За наведеною формулою можна обчислити ємність земної кулі. Середній радіус Землі R = 6380 км, тоді С = 4 ∙ 3,14 ∙ 8,85 · 10^-12_­­ · 6380· 10³ 0,7110^-3 Ф.

2.2. Конденсатори. Струм конденсатора. Енергія електричного поля

Пристрій із двох провідних тіл (пластин) будь-якої форми, розділених електриком, називають конденсатором (рис. 2.3). Пластини конденсатора часто називають обкладками. Прикладом природних конденсаторів можуть бути провідники електричної мережі, провідник електричної мережі та земля, дві жили кабелю, жила кабелю і панцер, прохідний ізолятор (який ізолює провід від стіни або металевого корпусу) тощо. Конденсатор під дією прикладної напруги має властивість швидко нагромаджувати та утримувати на своїх об­кладках однакові за величиною, але протилежні за знаками електричні заряди +q і –q. Ємністю конденсатора називають коефіцієнт пропорційності між за­рядом q та напругою U між обкладками конденсатора:

, або .

(2.4)

В

Рис. 2.3. Конден­сатор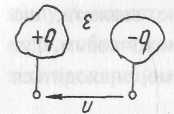

системі СІ одиницею вимірювання ємності є фарада (Ф). Одна фарада – це ємність такого конденсатора, який заряджається зарядом в 1 Кл при напрузі 1 В, тобто 1Ф = 1 Кл/1 В. Фарада – це дуже велика одиниця, тому на практиці часто вживають похідні одиниці, такі, як мікрофарада (1 мкФ = 10^-6 Ф), нанафарада (1 нФ = 10^-9 Ф) та пікофарада (1 пФ = 10^-12 Ф), чи 1Ф = 10^-6 мкФ = 10^-9 нФ = 10^-12 пФ).

Н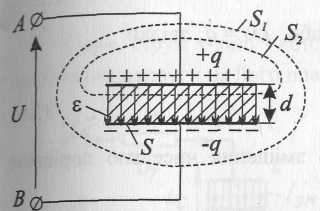 аведемо вирази ємностей конденсаторів деяких конструкцій.

Р

Рис. 2.4. До визначення ємності плоского конденсатора

озглянемо плоский конденсатор (рис. 2.4). Площа обкладок – S, відстань між обкладками – d, діелектрична проникність діеіектрика між пластинками – ε. Відстань d будемо вважати набагато меншою від лінійних розмірів обкладок конденсатора. У цьому випадку можемо нехтувати крайовим ефектом електричного поля конденсатора – випинанням силових ліній на краях конден­сатора.

Розглянемо замкнену поверхню Si, всередині якої є конденсатор із заряд­женими пластинками "+q" та "–q". Із постулату Максвелла (1.6) стосовно цієї поверхні одержимо:

,

оскільки d ≠ 0, то у всіх точках цієї поверхні вектор електричного зміщення D = 0, а отже, і значення напруженості електричного поля (Е = D / ε) теж до­рівнює нулеві. Отже, електричне поле поза конденсатором відсутнє. Далі розгля­немо замкнену поверхню S₂, яка охоплює тільки одну пластинку конденсатора із зарядом +q. Площу S₂ можна подати так: S₂ = S + S₆, де S – площа конденсатора; S₆ – бокова поверхня – поза конденсатором, для якої = 0. Запишемо для поверхні S₂ постулат Максвелла: = +q, і розділимо на два інтеграли:

,

(2.5)

де = 0, як вже було показано вище для площини S₁.

Ураховуючи, що між пластинами конденсатора вектор перпендикулярний до S, а отже, збігається з d , тο кут ( ^d ) = 0 і рівність (2.5) набере вигляд:

чи , або , звідки

(2.6)

Як видно з (2.6), вектор електричного зміщення чисельно дорівнює густині заряду на поверхні пластини.

Ураховуючи, що D = εΕ, одержимо напруженість електричного поля між зарядженими пластинами плоского конденсатора Ε = D/ε = q/(εS). Напруга між пластинами конденсатора за визначенням (1.9) є:

. Тут кут між ( ) = 0, тому

і ємність такого конденсатора:

Отже, ємність плоского конденсатора дорівнює:

.

(2.7)

Аналогічно можна одержати ємність циліндричного конденсатора завдовжки l та радіусами r₁ і r₂, r₂> r₁.

;

(2.8)

Ємність сферичного конденсатора радіусами r₁ та r₂:

.

(2.9)

Струм конденсатора. Якщо увімкнути незаряджений конденсатор до мережі постійної напруги, то він буде заряджатися: з мережі заряди проходять по провідниках на обкладки конденсатора. А рух зарядів по провідниках – це є електричний струм у колі з конденсатором: i = dq / dt. Виразивши із (2.4) заряд через ємність і напругу на конденсаторі, одержимо:

.

(2.10)

О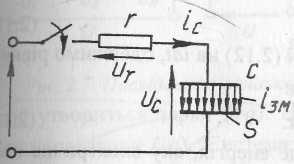 тже, струм у колі з конденсатором пропорційний його ємності й швид­кості зміни напруги на його пластинах.

Е

Рис 2.5. До визначення енергії електричного поля конденсатора

нергія електричного поля конденсатора. Схему (рис. 2.5) з незарядженим конденсатором (f/_c(0) = 0) увімкнено в мережу напругою U. Запишемо рівняння за другим законом Кірхгофа:

ri + u_c=U. (2.11)

Помножимо ліву й праву сторони рівності (2.11) на idt, одержимо рівнян­ня енергетичного балансу кола з конденсатором:

ri2dt + ucidt = Uidt.

(2.12)

Права частина (Uidt) рівняння (2.12) – це енергія, яку електричне коло забирає від мережі; перший член в лівій частині ri²dt – енергія, яка виділяється у вигляді тепла в опорі r. Оскільки енергія в конденсаторі не виділяється¹, то член u_Сidt є електричною енергією, яка накопичується у вигляді енергії електричного поля в конденсаторі. При заряджанні конденсатора протягом ча­су t до напруги U_С енергія електричного поля в кінці зарядження буде:

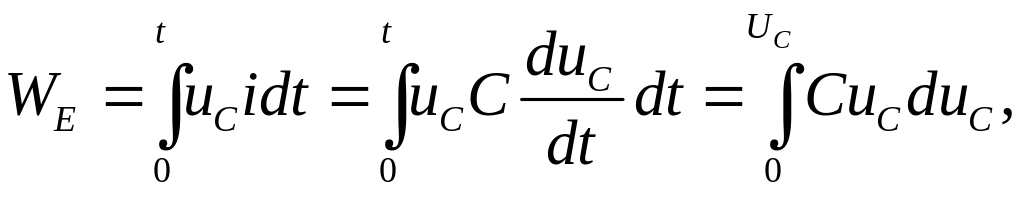звідки

(2.13)