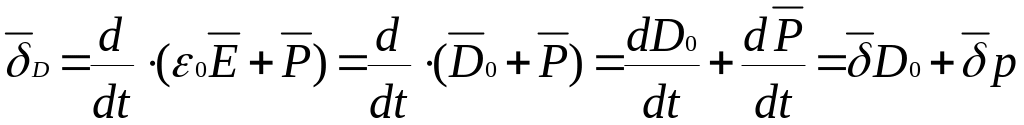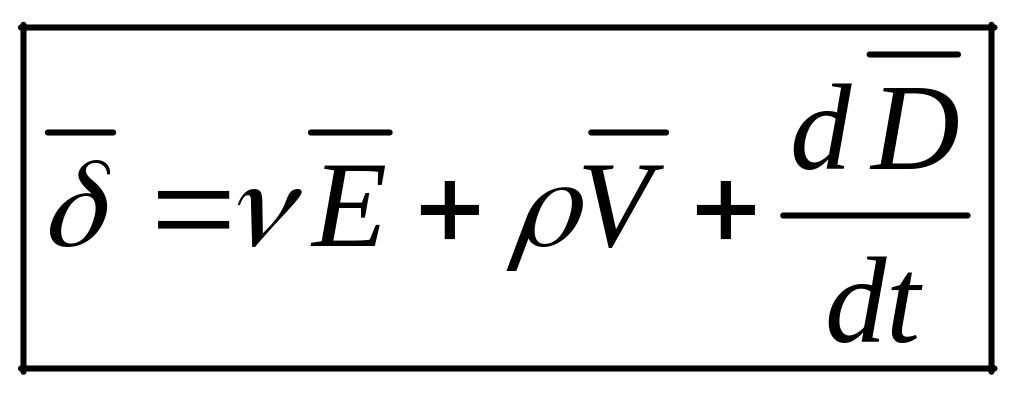1.5. Електричний струм і принцип його неперервності

Під електричним струмом розуміємо явище спрямованого руху носіїв електричних зарядів (струм вільних зарядів) та зміну електричного поля в часі (струм зміщення). Обидва ці явища супроводжуються появою магнітного поля. Додатним напрямом електричного струму прийнято вважати напрям руху но­сіїв позитивних зарядів.

Основними видами електричного струму є: струм провідності, струм пе­реносу (конвекції) та струм зміщення. Розглянемо їх окремо.

Струмом провідності називають упорядкований рух заряджених час­тинок всередині провідника під дією електричного поля. Струм провідності зумовлений наявністю вільних електронів (у металах), іонів (в електролітах). Ре­човини з такою провідністю називаються провідниками. Це, як правило, метали и електроліти, які мають електронну та іонну провідність.

Сила електричного струму (чи просто електричний струм) визначається кількістю заряду, що проходить крізь поверхню за одиницю часу, тобто

(1.19)

Якщо за однакові проміжки часу через поперечний переріз провідника проходить різна кількість заряду, струм вважається змінним і миттєве значення його визначається за (1.19); якщо за однакові проміжки часу через поперечний переріз провідника проходять однакові кількості заряду, струм називається постійним і визначається як

(1.20)

Диференційною мірою електричного струму є густина електричного струму (δ), значення якої знаходять із співвідношення

(1.21)

при перпендикулярному розташуванні струму di до площинки dS; δ є век­торною величиною. Густина струму провідності дорівнює

(1.22)

д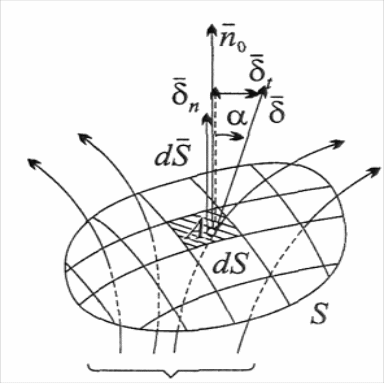 е γ – питома електрична провідність провідника; – вектор напруженості електричного поля. Користу­ються також питомим електричним опором ρ = 1 / γ, розмірність якого є Ом ∙ мм / м, чи Ом∙м.

Встановимо зв'язок у загальному випадку між силою електричного струму i та його густиною . Нехай через площу S (рис. 1.10) проходить струм, який зображений лініями струму i.

С

Рис. 1.10. До встановлен­ня співвідношення між струмом і та його густи­ною δ

трум через елемент поверхні dS дорівнює

Лінії струму і

,

а через всю поверхню S:

(1.23)

Вектор чисельно дорівнює площі і напрямлений по нормалі перпендикулярно до .

Струм переносу (конвекції) – це явище перенесення зарядів зарядже­ними частинками чи тілами, що рухаються у вільному просторі (рух зарядже­них елементарних частинок в пустоті, струм в електронних лампах, електрич­ний струм у газах тощо).

В

Рис. 1.11. До визна­чення струму пере­носу.

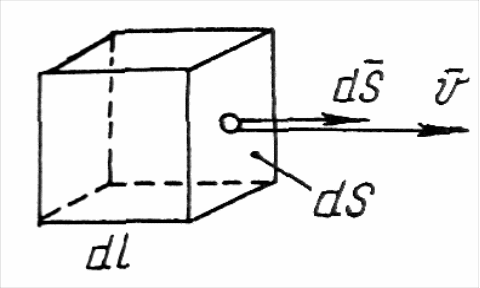
иділимо в просторі, в якому рухаються зі швидкіс­тю заряджені частинки з об'ємною густиною ρ, прямо­кутний паралелепіпед з елементарним об'ємом і з ребром , паралельним вектору (рис. 1.11). Заряд паралелепіпеда . Цей заряд за час проходить відстань . Отже:

Оскільки вектори і збігаються, то вектор густини струму переносу визначить: , отже, остаточно маємо:

(1.24)

В (1.24) [ρ] = 1 Кл∙м^-3 – об'ємна густина заряджених частинок, [ ] = 1 м ∙с^-1 –швидкість руху заряджених частинок.

Відзначимо, що для металевих і електролітичних провідників , і тому струмом переносу в цих провідниках нехтують.

Струм зміщення i_D існує за наявності змінного електричного поля в діелектрику чи в пустоті. Згідно з постулатом Максвелла під час внесення деякого заряду q у замкнену поверхню (рис. 1.4) крізь цю поверхню в напрямі зов­нішньої нормалі в діелектрику й пустоті проходить (змішується) такий самий за знаком і значенням заряд, причому зміна його пов'язана з вектором зміщен­ня співвідношенням (1.6) Отже і його гус­тина:

(1.25)

Враховуючи (1.5), густину струму зміщення (1.25) запишемо у вигляді:

(1.26)

Компонента – відповідає тут зміщенню заряду, зв'язаного з частинка­ми діелектрика (за рахунок поляризації діелектрика) крізь одиницю поверхні, перпендикулярної до напряму цього зміщення, під час зміни електронного поля (вектора напруженості Е) в діелектрику. Отже, він має наочне фізичне пояснення.

Компонента характеризує процес, що відбувається під час зміни електричного поля в пустоті (тобто в просторі, де відсутні відомі нам частинки матерії), і його називають вектором густини струму зміщення в пустоті. Наочної інтерпретації цього струму при сучасному стані науки дати не можна, ос­кільки ми ще не знаємо внутрішньої структури електромагнітного поля та внутрішніх процесів, що в ньому відбуваються.

У загальному випадку, остаточно, вектор густини струму визначається сумою всіх компонентів:

(1.27)

У колах постійного струму D(T) = const, отже, , і, ураховуючи ще, що , остаточно для кіл постійного струму маємо:

(1.28)

Якщо позначити повний електричний струм

(1.29)

і враховувати (1.27), то для будь-якої замкненої поверхні можемо записати:

(1.30)

що є загальним виразом принципу неперервності електричного струму, згідно з яким повний електричний струм крізь замкнену поверхню в будь-якому сере­довищі дорівнює нулеві. Його ще називають принципом замкненості елек­тричного струму.

Рис. 1.12. Скерування гус­тини струму, напруже­ності електричного поля

в провіднику рівного поперечного перерізу.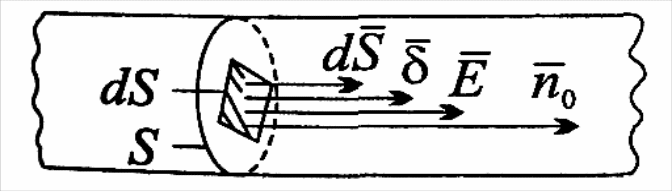

Лінії електричного струму неперервні, не мають ні початку, ні кінця – утворюють замкнуті контури. Це випливає з принципу неперервності електричного струму.

Якщо розглянути провідник однакового попе­речного перерізу по всій довжині й в якому струм розподіляється рівномірно по всій його площі попе­речного перерізу S (рис. 1.12), то вектори, збігаються. Враховуючи з (1.21), будемо мати, що:

чи

(1.31)

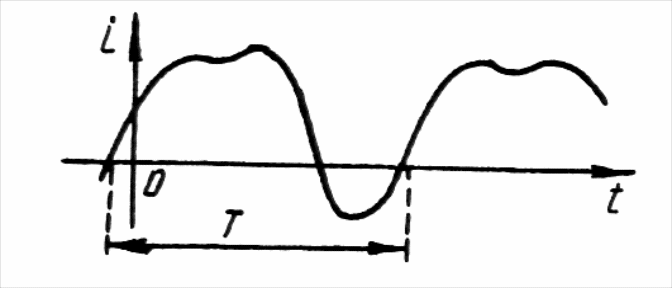
У загальному випадку струм у часі може змінюватися довільно, як зоб­ражено на рис. 1.13, що спостерігається, наприклад, під час перехідних проце­сів, які виникають в електричних колах при переході від одного до іншого їх стану.

Якщо зміна електричного струму в часі повторюється з деяким періодом Т (рис. 1.14), то такий струм називають змінним періодичним, або просто періодичним.

Рис. 1.13. Струм змінюється довільно

Рис. 1.14. Періодично змінний струм

Якщо струм в часі змінюється гармонійно – за синусоїдним законом (рис. 1.15), його називають синусоїдним струмом. В зв'язку з цим часто періодичний несинусоїдний за формою струм називають несинусоїдним. Незмінний в часі електричний струм (рис. 1.16) називають постійним і позначають великою літерою I.

Рис. 1.15. Синусоїдний струм

Рис. 1.16. Постійний струм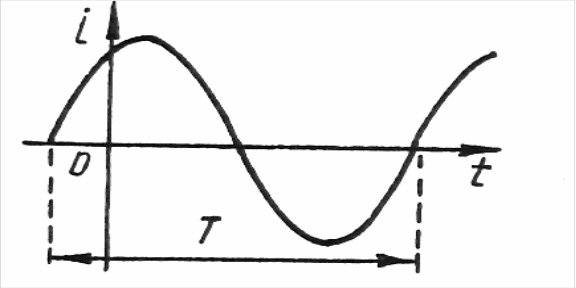

Додатним напрямом струму прийнято вважати напрям руху носіїв пози­тивних зарядів. У вітках схем електричних кіл умовно-додатний напрям струму позначають стрілками. Якщо в колі є тільки одне джерело постійної ЕРС, то до­датні заряди будуть рухатися через вітку з ЕРС в напрямі стрілки ЕРС. Тому для того, щоб одержувати при розрахунках додатні значення струму через дже­рело, якщо в схемі діє тільки одна ЕРС, треба вибирати умовно-додатний на­прям струму, який збігається з напрямом дії ЕРС.

Одиниця сили струму є ампер і є однією з основних одиниць системи СІ:

Похідні одиниці це 1 міліампер (1 мА = 10 ^-3А); 1 мікроампер (1 мкА = 10^‑6А); 1 кілоампер (1кА = 10 ³А).