Зайві ступені вільності і умови зв'язку

Під час дослідження структури механізмів можуть виявитися ступені вільності та умови зв'язку, що не впливають на ру­хомість механізму в цілому. Такі ступені вільності і умови зв'яз­ку називають зайвими.

Як приклад, на рис. 2.12 зображено схему кулачкового механізму, до складу якого входить стояк 0, кула­чок 7, штовхач 2, ролик 3. Стояк і кулачок утворюють обертову пару V класу, кулачок і ролик — пару IV класу, штовхач і стояк — поступальну пару V класу, штовхач і ролик — обертову пару V класу. Тоді, виходячи з числа рухомих ланок і кінематичних пар, ступінь вільності механізму за формулою Чебишова:

W = 3n – 2 p₅ – p₄ = 33 – 23 – 1 = 2

Проте очевидно, що у цьому механізмі досить знати поло­ження одного кулачка, щоб однозначно визначити положення штовхача, тобто досить мати одну початкову ланку, а не дві, як це випливає з формули Чебишова. В цьому механізмі ролик 3 створює зайвий ступінь вільності, він може перекочуватися і ковзати відносно кулачка, що не впливає на характер руху штовхача. Ролик є конструктивним елементом, який введено для заміни тертя ковзання тертям кочення, тобто для зменшен­ня опору сил тертя і зношення ланок. Кінематика механізму не змінюється, якщо ролик забрати і штовхач 2 безпосередньо з'єднати з кулачком 1у кінематичну пару IV класу (на рис. 2.12 цей випадок показано штриховою лінією).

На рис. 2.13 зображено механізм спарника (паралельних кри­вошипів), з розмірами ланок: АВ = СD, АD = ЕF = ВС, АЕ = DF і ВЕ = СF. За кількістю рухомих ланок (n = 4) і пар V класу (p₅ = 6) ступінь вільності механізму W = 0, тобто цей кінематичний ланцюг є нерухомою фермою. Проте, коли ланка ЕF паралельна ланці ВС, механізм має один ступінь вільності (W = 1), оскільки фігура АВСD завжди утворює паралелограм, і, отже, відстань між точками Е і F ніколи не змінюється і дорівнює відстані між точками А і D або В і С. Тоді без усякого порушення характеру руху механізму ланку ЕF (або ВС) можна забрати, оскільки ця ланка накладає на рух механізму зайві (пасивні) зв'язки, тобто нові зв'язки на вже існуючі. На практиці вводять ланку ЕF для збільшення жорсткості механізму.

Під час проведення структурного аналізу механізму не­обхідно позбутися зайвих ступенів вільності і пасивних зв'язків.

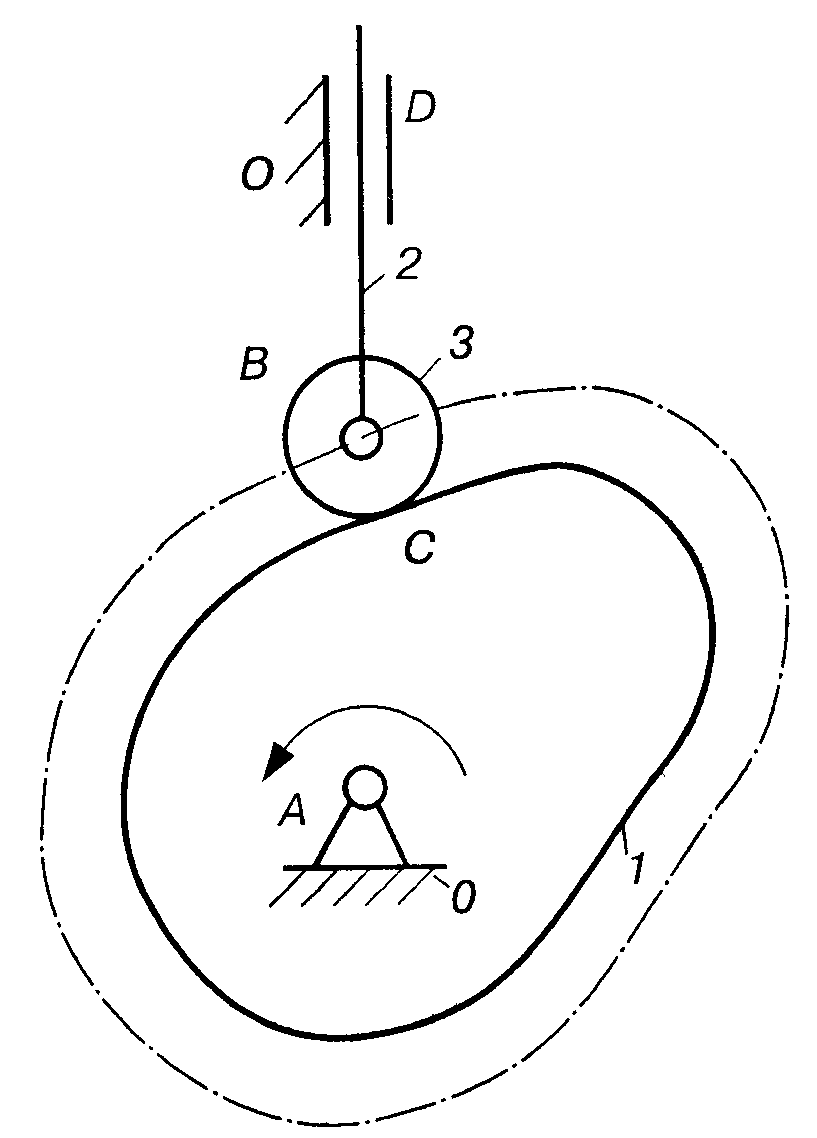
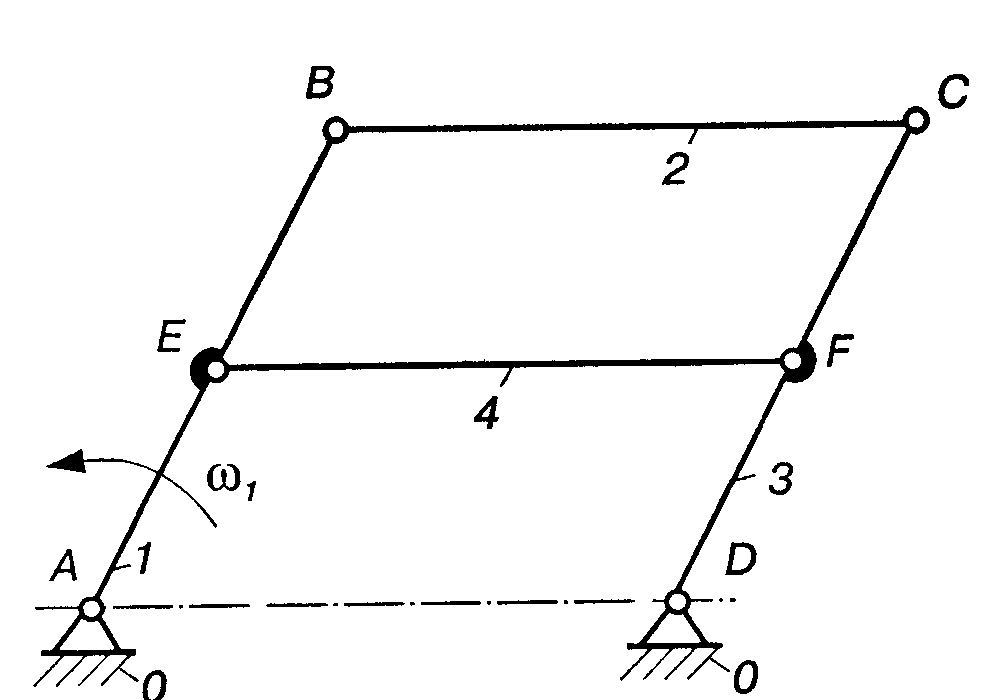
Рис. 2.12 Рис. 2.13

Заміна вищих кінематичних пар нижчими

При структурному аналізі механізмів вищі кінематичні пари зручно замінити нижчими. При цьому має задовольнятися умо­ва структурної еквівалентності, тобто щоб замінний механізм мав таке саме число ступенів вільності і щоб характер миттєвого відносного руху не змінився.

На рис. 2.14 зображено схему триланкового плоского механізму з двома обертовими парами (А і В) та однією вищою парою С, утвореною ланками 7, 2 Профі­лями елементів пари С є дві дуги кіл з центрами К₁ і K₂. Ступінь вільності такого механізму:

W = 3n – 2p₅ – p₄ = 3 2 – 22 – 1 = 1. (2.4)

Незважаючи на те що точка С дотику профілів ланок 2, З під час руху механізму змінює своє положення, відстань К₁K₂ = r₁+r₂ = const. Тому заданий механізм буде еквівалентний плоскому шарнірному чотириланковому механізму (рис. 2.14,б), в якого довжини відрізків АК₁, К₁K₂, ВК₂ такі самі, як на рис. 2.14, а, і ступінь вільності:

W = 3n – 2p₅ – p₄ = 33 – 24 – 0 = 1. (2.5)

Замінний механізм АК₁K₂В еквівалентний заданому і за за­коном руху ланок, тобто зберігається відношення швидкостей ₁/₃.

Порівнюючи механізми, зображені на рис. 2.14,а,б, та за­лежності (2.4) і (2.5), бачимо, що вища пара у плоских ме­ханізмах еквівалентна одній умовній ланці і двом кінематичним парам V класу.

Розглянутий спосіб заміни механізму можна узагальнити й тоді, коли профілями вищих пар є криві змінної кривизни і ма­ють спільну дотичну в точках спряження профілів (рис. 2.14,в). Однак у цьому випадку кожному положенню механізму відпові­дають різні еквівалентні "миттєві" шарнірні чотириланкові ме­ханізми АК₁K₂В, у яких К₁ і К₂ є миттєвими центрами кривизни профілів, що відповідають точці С дотику.

Таким чином, щоб замінити вищу кінематичну пару ниж­чою, необхідно ввести додатково умовну ланку з двома обер­товими кінематичними парами V класу, центри шарнірів яких треба розмістити у центрах кривизни профілів ланок, що утворюють цю вищу пару, і заново введену ланку слід з'єдна­ти нижчими парами з тими ланками, які входили до складу вищої пари.

Рис. 2.14