Підставляючи (11.22) у рівняння (11.10), знаходимо:

звідки, враховуючи, що дістаємо:

(11.23)

Аналогічно можна одержати формулу для визначення мо­менту інерції маховика через точки перетину дотичних з віссю абсцис першої системи координат.

Лекція 12

НЕРІВНОМІРНІСТЬ І РЕГУЛЮВАННЯ РУХУ

МЕХАНІЗМІВ І МАШИН

(ПРОДОВЖЕННЯ)

Визначення розмірів маховика

Оскільки маховик звичайно роблять у вигляді колеса (рис. 12.1), який має масивний обід 1, сполучений з втулкою 2 спицями 3 (або тонким диском), то моментами інерції з'єднуючих частин часто нехтують і набли­жено вважають, що маса маховика рівномірно розподілена по колу радіуса — гео­метричному місцю центрів ваги поперечних перерізів обода. Тоді момент інерції маховика можна виразити так:

(12.1)

де т — маса маховика.

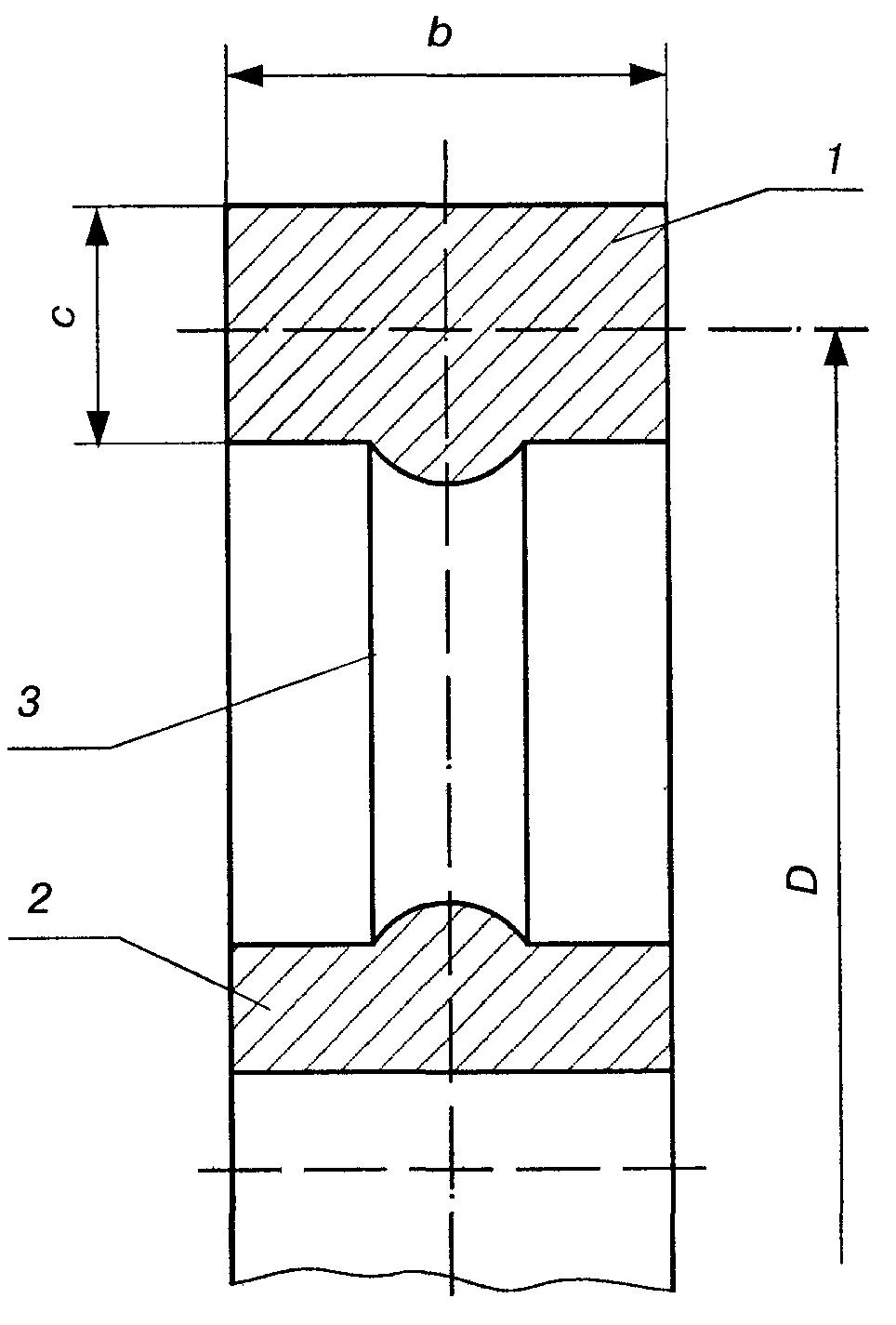
Рис.12.1

Добуток маси обода ма­ховика на квадрат його діа­метра називається маховим моментом, або характеристикою маховика. Для ба­гатьох деталей машин, що здійснюють обертовий рух (муфти, ротори електродви­гунів тощо), ця характери­стика наводиться у довідни­ках. Характеристика маховика має одиницю виміру кг  м². За цією характеристикою можна легко визначити не­обхідну масу маховика, якщо задано або вибрано його діаметр, значення якого визначається з суто конструктивних міркувань. Для запобігання небезпеці можливого розриву маховика його діаметр вибирають таким, щоб колова швидкість на ободі не пе­ревищувала допустиму для матеріалу маховика величину.

Для пе­ревірки діаметра маховика можна рекомендувати таку залежність:

(12.2)

Де — допустима колова швидкість обода маховика, яка не повинна перевищувати для стальних маховиків 70-120 м/с, для чавунних — 30-45 м/с; п — частота обертання маховика, .

Якщо маса обода маховика практично може бути взята як

де — маса обода маховика, то ширина обода маховика ви­значається з виразу

(12.3)

Тут - густина матеріалу, кг/м³; . Тоді, якщо взяти = 7800 кг/м³, матимемо:

(12.4)

Регулятори швидкості

За допомогою маховика можна регулювати швидкість руху лан­ки зведення механізму або машини лише для періодичних і ко­роткочасних неперіодичних коливань швидкості, тобто коли рушійні сили і сили опору, як правило, змінюються протягом циклу за певним законом і робота рушійних сил за повний цикл дорівнює роботі сил опору. Крива Віттенбауера при такому русі замкнута і має цілком визначену форму.

Проте маховик не може регулювати довгочасні і неперіодичні коливання швидкості, коли робота рушійних сил не дорівнює роботі сил опору. Наприклад, навантаження на двигун внутрішнього згоряння автомобіля значно зростає внаслідок крутого підйому дороги. Це викликає значну зміну моменту сил опору на валу двигуна, у результаті чого порушується рівновага між роботами рушійних сил двигуна і сил опору руху авто­мобіля, що викликає зменшення його швидкості. І навпаки, при крутому спуску швидкість автомобіля може значно зростати до значення, яке буде більшим за встановлене з точки зору безпеки руху. Водій автомобіля здійснює регулювання швидкості руху за рахунок зміни роботи рушійних сил (додатковою подачею пали­ва в двигун) або включення додаткової роботи сил опору (гальмуванням). Це дає змогу зберігати відповідний баланс робіт.

Таким чином, для забезпечення коливання швидкості — ланки зведення в заданих межах — треба, щоб у машині за один цикл підтримувалась рівність робіт рушійних сил і сил опору ( ). Для цього, як правило, встановлюють спеціальні ме­ханізми, — пристрої, які називають регуляторами швидкості. Завдання регулятора полягає в тому, щоб встановити стійкий (стаціонарний) за законом зміни значення швидкості режим руху початкового вала механізму або машини, чого можна досягти вирівнюванням різниці між рушійними силами і силами опору. Так, якщо внаслідок якихось причин зменшився опір і машина починає прискорювати свій рух, то регулятор автоматично зменшує рушійні сили. Навпаки, якщо сили опору збільшилися і машина починає сповільнювати рух, то регулятор збільшує рушійні сили. Отже, як тільки порушується рівновага між рушійними силами і силами опору, регулятор повинен знов їх збалансувати і змусити машину працювати з попередніми або близькими до попередніх швидкостями. У деяких машинах, зокрема в транспортних, регулювання руху досягається зміною не тільки рушійних сил, а й сил опору (гальмуванням).

Конструкції регуляторів і схеми регулювання бувають різними. Наприклад, у практиці застосовуються: так звані відцентрові регулятори (плоскі й просторові), в яких використо­вується відцентрова сила інерції; інерційні регулятори, в яких використовують тангенціальні (дотичні) сили інерції; регулятори електричного типу та ін.

Хоча конструкції механізмів регуляторів і схем регулювання різні, проте частіше автоматичне регулювання виконується за схемою замкненого контуру. Принципова схема такого авто­матичного регулювання зображена на рис. 12.2.

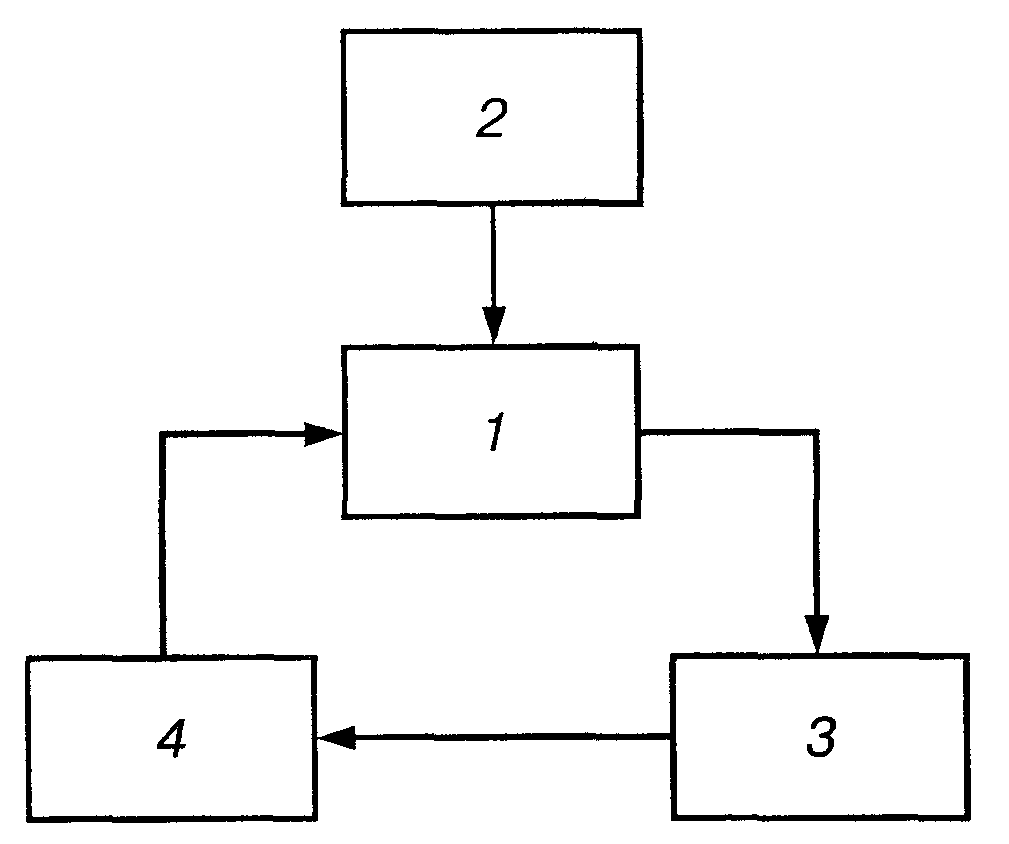
Рис. 12.2

Об'єкт регулювання 1 знаходиться під дією зовнішнього джерела збудження коливань 2, в результаті чого здійснюється відхилення парамет­ра, що регулюється, від заданого. Ці зміни сприймаються чутли­вим елементом 3, який передає необхідну інформацію регулю­вальному органу 4, останній відновлює заданий параметр у об'єкта регулювання 1, тобто в схемі регулювання є зворотний зв'язок (1-3-4-1).

На рис. 12.2 зображено найпростішу схему системи автома­тичного регулювання, в яку входять різні додаткові пристрої, що забезпечують надійність роботи цієї системи.

У машинному агрегаті об'єктом регулювання, звичайно, є двигун, а джерелом збудження — робоча машина, яка приво­диться в рух цим двигуном. Чутливим елементом може бути ме­ханічний пристрій, частіше механізм регулятора відцентрового типу, або електричний типу тахогенератора, який є електричним генератором, що розвиває напругу пропорційно кутовій швидкості. Ця напруга діє на регулювальний орган. Такі органи мо­жуть бути різними залежно від технологічного призначення машини і типу двиуна.

Розглянемо деякі схеми автоматичного регулювання кутової швидкості початкової ланки машинного агрегату.

На рис. 12.3 зображено машинний агрегат, який складається з робочої машини 2 і теплового двигуна 1.

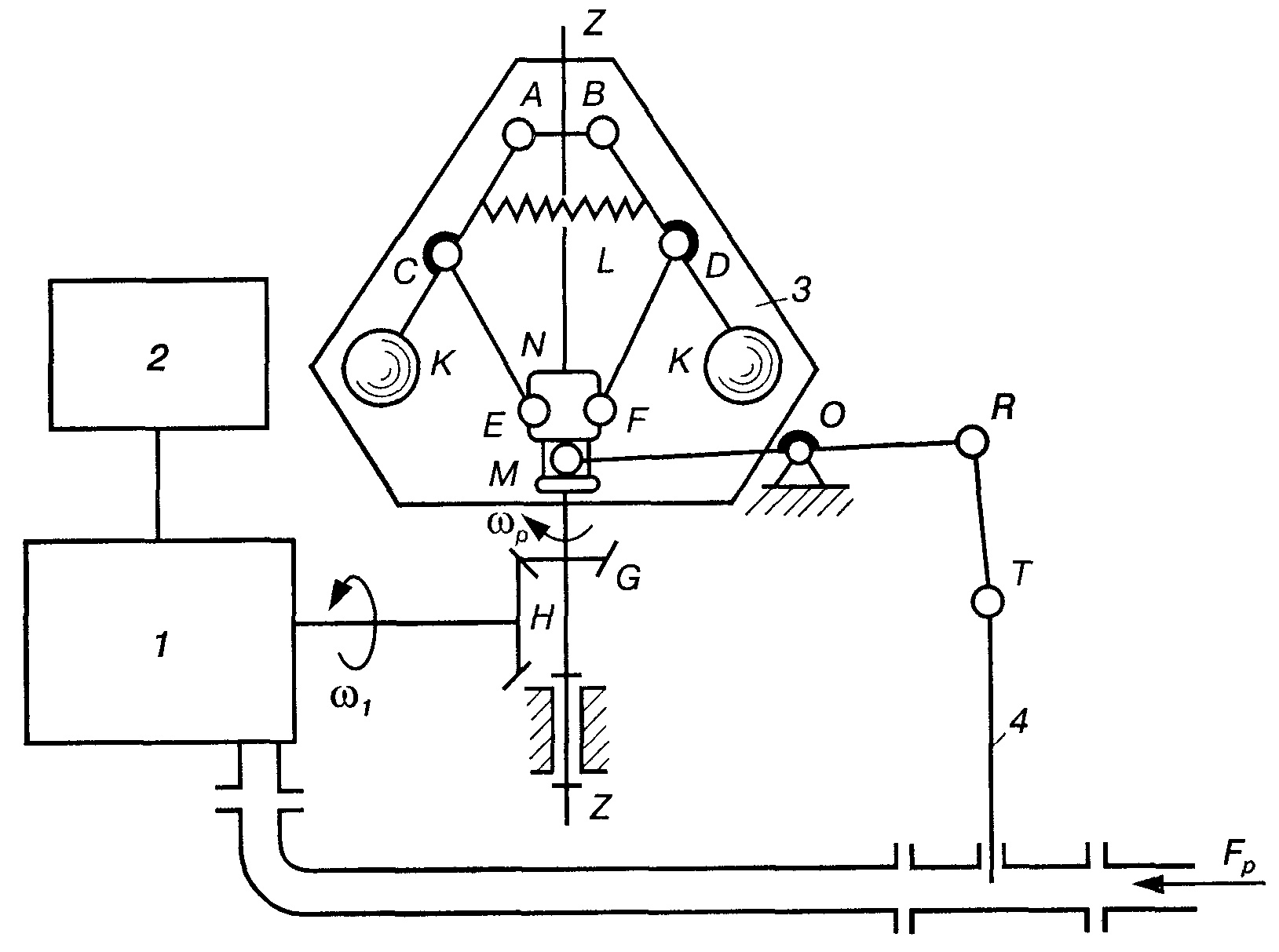
Рис.12.3

Чутливим елементом є відцент­ровий регулятор 3. Регулятор складається з двох важких куль К, що розміщені на ланках АС і ВD. Ці ланки шарнірно зв'язані з ланками СЕ і DF, які, у свою чергу, шарнірно зв'язані з муфтою N. що може вільно ковзати вздовж напрямної . Ланки АС і ВD зв'язані пружиною L, яка нама­гається зблизити кулі К. Ре­гулятор приводиться в рух від початкової ланки маши­ни парою конічних коліс Н і G. При обертанні початкової ланки двигуна з кутовою швидкістю регулятор обертається зі швидкістю , причому

При різних кутових швидкостях початкової ланки муфта N має різні положення, які визначаються величиною відцентрової сили інерції, що діє на кулі К. Чим більше швидкість обертання вала регулятора, тим більші сили інерції діють на кулі, тим вище піднімається муфта N, і навпаки, чим менша швид­кість , тим менші сили інерції діють на кулі, а значить, нижче знаходиться муфта N. З муфтою N з'єднано механізм, що збіль шує або зменшує подачу рушійної енергії в маши­ну. Цей механізм скла­дається з важелів ОR і RТ і заслінки 4. Палець М, який належить важелю ОR, ковзає по напрямних, що належать муфті N. Припустимо, що внаслі­док зменшення сил опору кутова швидкість регу­лятора збільшилась. Тоді тягарі К під дією відцент­рових сил віддалятимуться від осі обертання ре­гулятора, і муфта N пе­реміщатиметься вгору. При цьому важіль RТ діятиме на заслінку 4, яка, опус­каючись донизу, змен­шить переріз каналу, по якому надходить у двигун робоча речовина (пара, вода, газ тощо). Тоді ру­шійні сили зменшаться, кутова швидкість також зменшиться, і муфта N почне переміщатися вниз. Отже, заслінка 4 пере­міщатиметься вгору, збільшуючи переріз каналу. Після збільшення подачі рушійної енергії процес може знову повторитися.

Отже, робота регулятора — деякий коливальний процес.

Регулятор автоматично реагує на зміну кутової швидкості початкової ланки двигуна і забезпечує подачу необхідної енергії для пересування регулю­вального органа. Треба зазначити, що описаний спосіб регулюван­ня має той недолік, що після зниження навантаження кутова швидкість буде трохи вищою від тієї, яку мала машина до знижен­ня навантаження, хоч рух машини і буде усталеним, але швидкості цього руху будуть вже іншими і дещо більшими, ніж на початку процесу регулювання. Щоб уникнути зазначеної зміни швидкості, у техніці часто застосовують складніші схеми регулювання.

Описаний тип регулятора називається регулятором прямої дії, оскільки в ньому регулятор безпосередньо з'єднаний з ме­ханізмом, що регулює подачу рушійної енергії. У розглянутому прикладі заслінка переміщується за рахунок відцентрових сил куль регулятора. У деяких випадках цих сил може бути не до­сить для переміщення заслінки, тоді слід включити в схему ре­гулювання допоміжне джерело енергії, яке називають сервомо­тором. Такі регулятори називаються регуляторами непрямої дії.

На рис. 12.4 показано схему непрямого регулювання. Ця система має ті самі основні елементи, що й схема прямої дії (див. рис. 12.3). Тільки тут переміщення регулювального органа 4 (заслінки) здійснюється за допомогою гідравлічних сервомоторів.

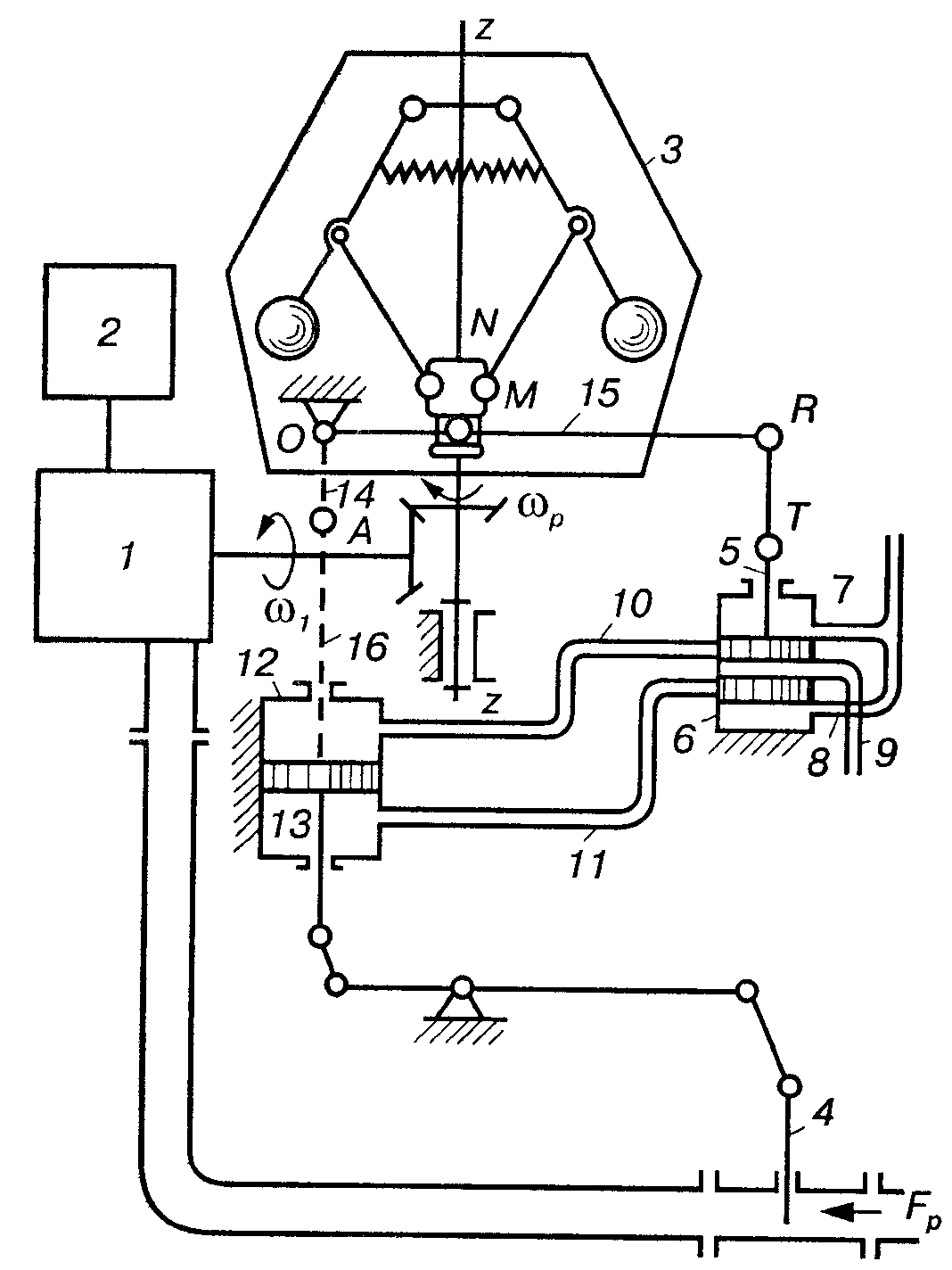
Рис.12.4

Рух регулюється так. При збільшенні кутової швидкості сої початкової ланки машини муфта N почне підніматися і через систему важелів підніме золотник 5; масло по трубопроводах 8 і 11 надходить у нижню порожнину циліндра 12 сервомотора, поршень 13 переміститься вгору і системою важелів опустить заслінку 4, зменшуючи доступ рушійної енергії . При русі поршня 13 уверх масло, яке знаходиться у верхній порожнині циліндра 12, по трубопроводах 9 і 10 подається в маслоприймач. Після того як заслінка 4 опуститься, кутова швидкість зменшиться, муфта почне опускатися вниз, золотник 5 перекриє трубопроводи 10, 11 і доступ масла в циліндр 12 сервомотора припиниться. Після повернення золотника 5 в таке положення процес регулювання має закінчитися.

Чутливість регулятора до зміни швидкості початкової ланки і коефіцієнт нерівномірності руху визна­чаються відповідним підбором мас куль К, силою пружності пружини L, масами і розмірами ланок механізму регулятора.