Лекція 10 важіль м.Є. Жуковського

У тому разі, коли нема потреби робити повний силовий розра­хунок механізму, в результаті якого визначаються реакції в кінематичних парах (наприклад, розрахунок потужності двигу­на), задача зводиться тільки до визначення зрівноважувальної сили або зрівноважувального моменту, який прикладають до початкової ланки. Реакції в кінематичних парах можуть залиша­тися невідомими як внутрішні сили для всього механізму в цілому. У таких випадках для знаходження зрівноважувальної сили користуються методом (правилом) так званого жорсткого важеля М.Є.Жуковського.

Правило М.Є.Жуковського грунтується на використанні принципу можливих переміщень:

Якщо на будь-яку механічну систему діє ряд сил, то, приєд­навши до заданих сил сили інерції і надавши всій системі мож­ливих для даного її положення переміщень, дістанемо ряд еле­ментарних робіт, сума яких дорівнює нулю.

Для механізму, в якому ланки здійснюють визначений рух, можливі переміщення стають дійсними переміщеннями. Тоді, якщо на ланки механізму діє ряд сил принцип можливих переміщень можна виразити в такому вигляді:

(10.1)

або:

де — дійсне нескінченно мале переміщення точки прикла­дання сили (і = 1,2,3,..., n); — кут між напрямком сили , і напрямком переміщення точки прикладання сили. Поділивши рівняння (10.1) на dt, дістанемо

(10.2)

де — швидкість точки прикладання сили ; — миттєва потужність, що розвивається силою .

Рівняння (10.2) показує, що принцип можливих переміщень можна виразити через суму миттєвих потужностей сил, що діють на ланки механізму.

Для окремо взятої ланки АВ (рис. 10.1, а), на яку діє сила прикладена в точці С (швидкості точок А і В задані, точка Р — миттєвий центр швидкостей), миттєва потужність, що розвиває ця сила,

може бути виражена по-іншому. Для цього побудуємо поверну­тий на 90° проти миттєвого обертання ланки АВ план швидко­стей цієї ланки (рис. 4.25, б), у точку с якого прикладемо силу і запишемо момент сили відносно полюса р:

(10.3)

де — плече сили відносно полюса р; рс — відрізок на плані швидкостей, який у масштабі визначає швидкість точки С, тобто . Тоді, помноживши ліву й праву частини (10.3) на , дістанемо:

(10.4)

Такі самі вирази можна записати і для сил, що діють на інші ланки механізму. Просумувавши їх, дістанемо рівняння, яке буде тотожне рівнянню (10.2), сума членів якого дорівнює нулю, тобто:

Рис. 10.1

або після скорочення на маємо:

(10.5)

Рівняння (10.5) і є записане в математичній формі правило важеля М. Є. Жуковського, яке можна сформулювати так:

Переносимо всі задані сили, що діють у даний момент часу на ланки механізму, в тому числі й сили інерції, в однойменні точки повернутого плану швидкостей, не змінюючи при цьому величину і напрямок сили. Розглядаємо повернутий план швидкостей як дея­кий жорсткий важіль, який перебуває в рівновазі відносно полюса плану швидкостей під дією всіх прикладених сил. Тоді сума мо­ментів усіх цих сил, включаючи зрівноважувальну силу, відносно полюса плану швидкостей дорівнює нулю.

Така геометрична інтерпретація принципу можливих пе­реміщень дуже зручна для розв'язування задач динаміки ме­ханізмів. Метод цей дістав назву методу М. Є. Жуковського за ім'ям великого російського механіка, який його запропонував, а важіль, яким користуються у цьому методі, названо важелем Жуковського.

Метод Жуковського можна застосувати для знаходження значення будь-якої сили, якщо задано точку прикладання і на­прямок цієї сили, а також задано значення, напрямки і точки прикладання всіх інших сил. Справді, у цьому випадку в рівнянні (10.5) буде тільки одне невідоме значення шуканої си­ли, яка з нього визначається.

Якщо на ланки механізму, крім сил , діють ще пара сил, моментом яких є то при використанні правила Жуковсь­кого кожний момент (рис. 10.2) розкладають на пару сил , які прикладають у дві точки, наприклад А і В. Величину й напрямок кожної сили визначають за умови, що де , - плече сил , що дорівнює в нашому випадку (рис. 10.2) дов­жині ланки . При цьому напрямок моменту пари сил повинен збігатися з на­прямком моменту . Треба ма­ти на увазі, що напрямок цього моменту сил на важелі Жу­ковського може не збігатися з напрямком моменту на схемі механізму.

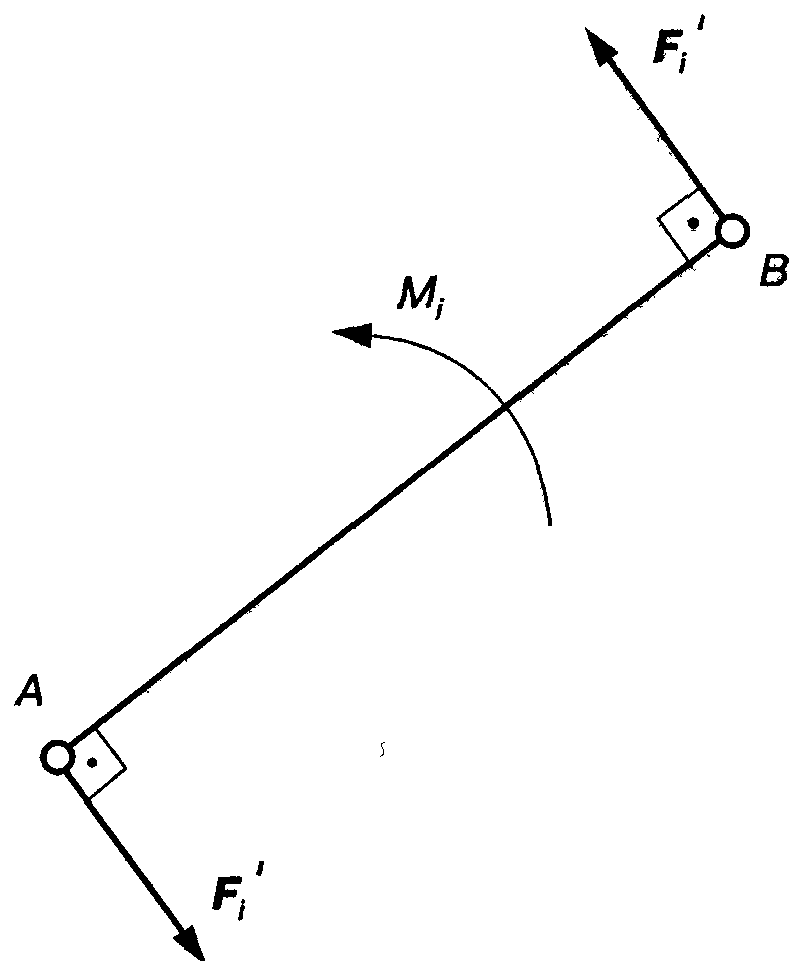
Рис. 10.2

Це буває тоді, коли положення точок А і В на ланці та на плані швидкостей (а і b) не збігаються.

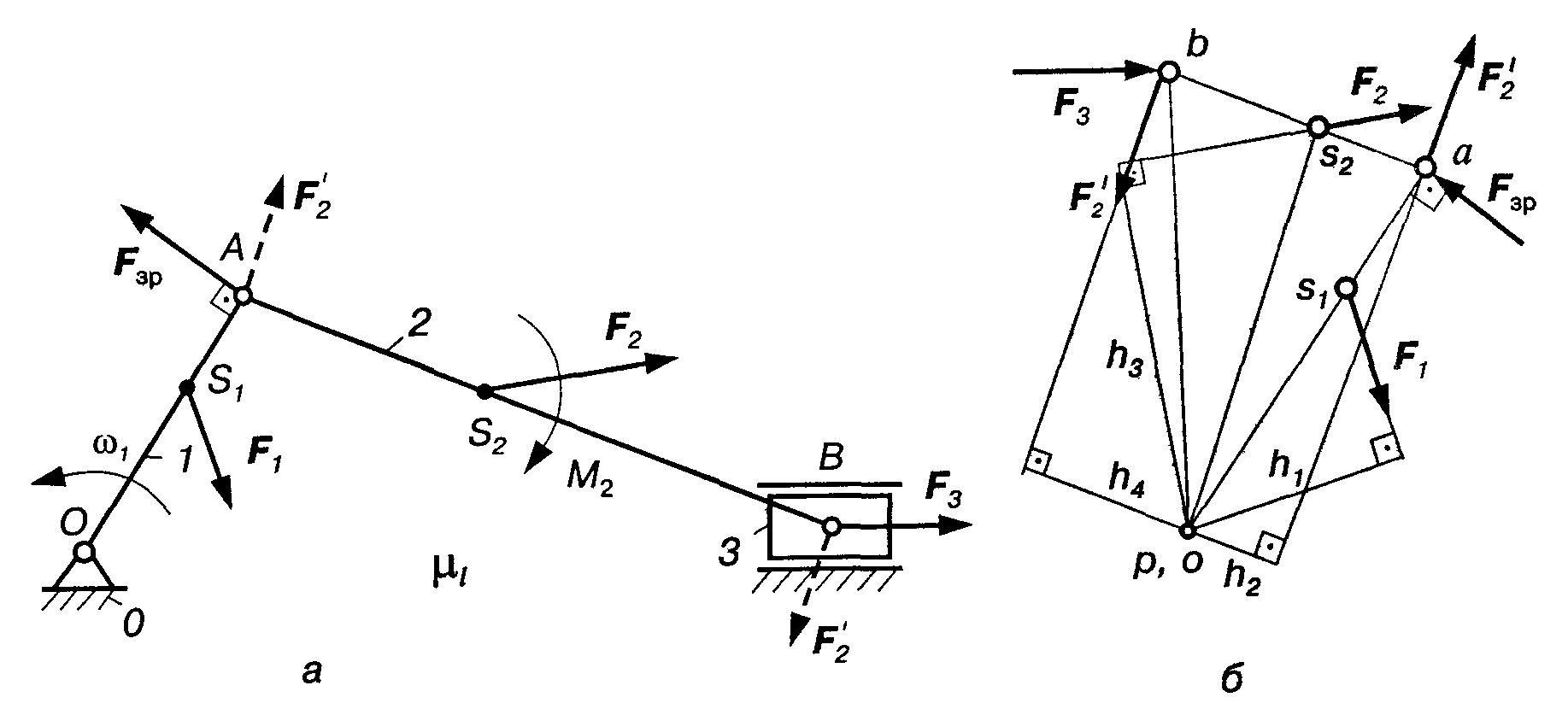
Рис. 10.3

Розглянемо приклад визначення зрівноважувальної сили за допомогою правила важеля Жуковського.

Приклад 10.1. Нехай задано кінематичну схему кривошипно-повзункового механізму (рис. 10.3,а), на ланки якого діють си­ли момент сил , швидкість обертання кривошипа ОА . Зрівноважувальну силу прикласти до кривошипа ОА у точці А і направити перпендикулярно до лінії ОА.

Розв'язання. Будуємо для заданого положення ме­ханізму повернутий на 90° проти миттєвого обертання криво­шипа сої план швидкостей (рис. 10.3,б) у відповідних точках якого прикладаємо сили момент розкладаємо на пару сил (на рис. 10.3,а сили показано штриховою лінією), які прикладаємо відповідно в точках а і b перпендикулярно до АВ .

Враховуючи, що під дією сил, включаючи Зрівноважувальну силу, механізм перебуває в рівновазі, можна записати таке рівняння всіх сил, що прикладені до повернутого плану швид­костей, який умовно приймаємо жорстким важелем:

звідки маємо:

(10.6)

де — плечі відповідних сил відносно полюса повернутого плану швидкостей, мм.

Напрямок вектора зрівноважувальної сили вибрано пра­вильно, якщо після числового розрахунку (10.6) одержимо зі знаком плюс і, навпаки, якщо знак буде мінус, то треба змінити напрямок вектора сили на протилежний.

Викладений метод є загальним для механізмів будь-якого класу.