Свойства полных и дробных факторных планов для линейных моделей

Матрица F для плана типа ( строк. столбцов) (исольз. 3 фактора).

Строим реплику:

Число оцениваемых коэффициентов 4, число опытов 4.

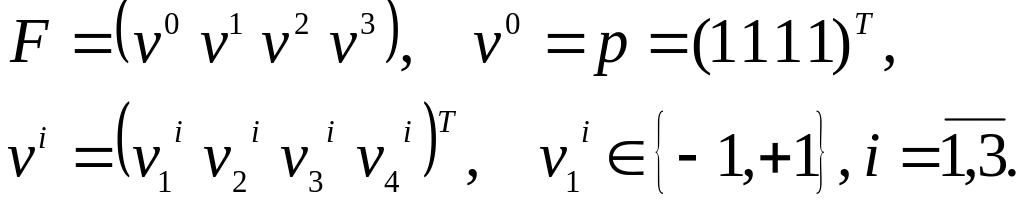
Найдем информационную матрицу:

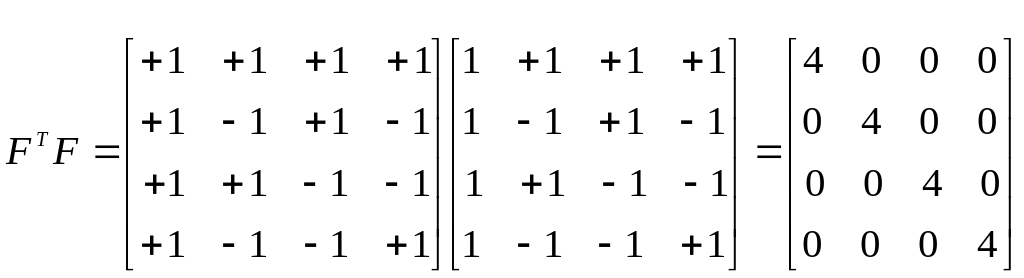
Для дисперсионной матрицы получаем:

.

Найдем оценки коэффициентов модели (принимаем во внимание вид дисперсионной матрицы):

-- строки,

-- скалярное произведение 2-х векторов.

Тогда можно оценить коэффициенты регрессии модели:

.

После определяем точность оценивания коэффициентов. Она характеризуется дисперсией оценок коэффициентов . Для этого находят ковариационную матрицу ошибок измерения коэффициентов:

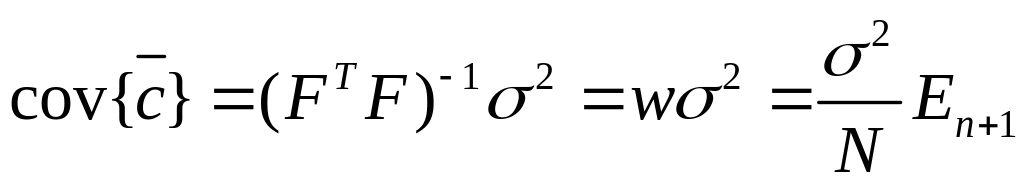
Видно, что ковариационная матрица диагональная, т.е. коэффициенты модели не связаны др. с др. Точность измерения, определяемая этой формулой выше, зависит от числа опытов (все коэффициенты определяются с одинаковой точностью).

.

Фактически, при планировании эксперимента задаются ошибкой измерения коэффициентов, и на основе этого определяют необходимое число опытов.

-- дисперсия ошибки наблюдения выходного сигнала объекта. Ее сложно определить, поэтому ее заменяют оценкой. Оценка вычисляется на основе остатков.

Технология проведения эксперимента

В каждой экспериментальной точке vⁱ, проводятся опытов

,

При одних и тех же входных сигналах получаются разные значения на выходе (из-за действия помехи). Рассчитывается среднее наблюдаемое значение:

(3)

Составляется вектор результатов экспери­мента

(4)

Оценка дисперсий:

• В каждой точке проводится один эксперимент

Оценка дисперсии ошибок наблюдений (остаточная сумма):

(5)

- число степеней свободы

Остаточная сумма, приходящаяся на 1 степень свободы, принимается за дисперсию ошибок:

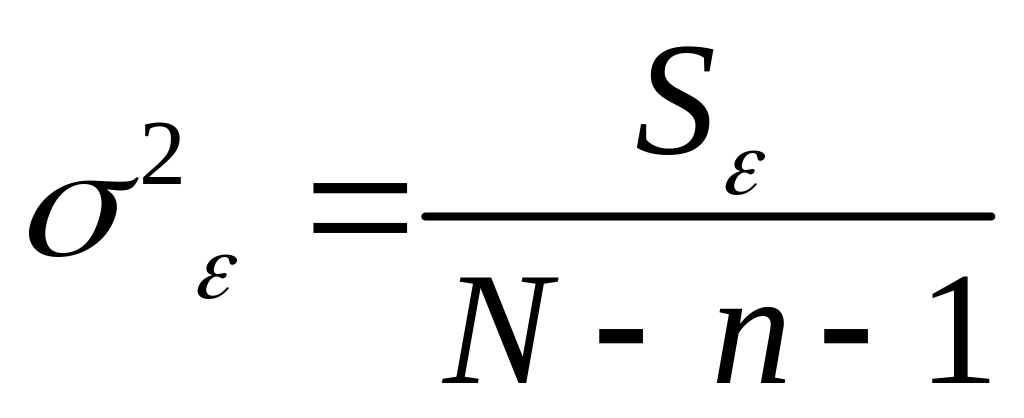(6)

Оценки дисперсий коэффициентов модели

(7)

Отношение фактической суммы к остаточной дает F-распределение:

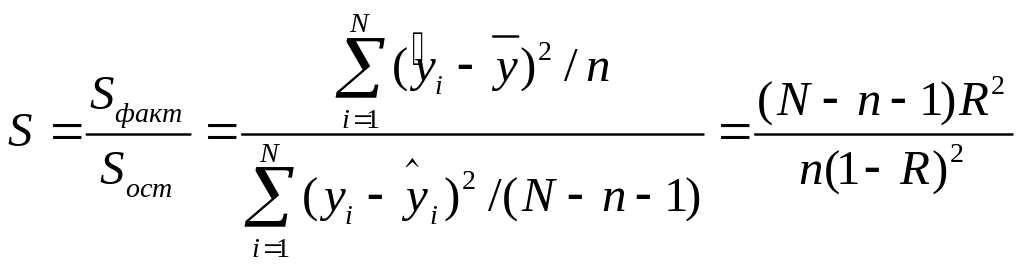
Затем определяется табличное значение F-распределения, которое обознач. Fт, оно сравнивается с расчетным F. F>Fт – модель значима.

• В каждой точке проводится экспериментов

Для оценки адекватности:

1) вычисляется сумма квадратов, характеризующая ошибки наблюдений выхода ОУ:

(8)

Nv – всего опытов, N – количество констант, которые определим.

После определяется дисперсия ошибок наблюдения выхода ОУ:

₍₉₎

_{Точность коэффициентов определяется ковариационной матрицей}

2) определяется сумма квадратов, характеризующая неадекватность (дефект) модели:

Находится расчетное значение критерия Фишера:

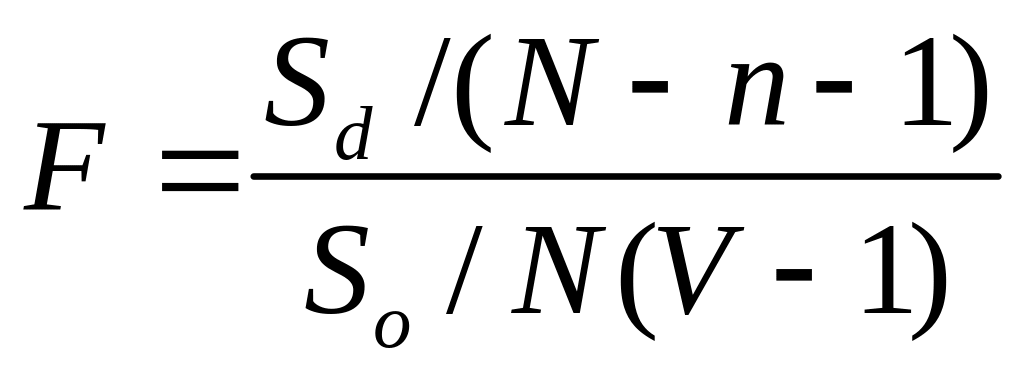(10)

Находят табличное Fт. Если F<Fт, то модель адекватна наблюдениям ОУ.