Идентификация с помощью настраиваемой модели
Задача: ОУ, подвергаемый идентификации имеет один вход и один выход и описывается ПФ известной структуры, т.е. известны порядки многочлена числителя и знаменателя.
Найти: Оценки коэффициентов ПФ.
Задача решается с помощью подстраиваемой модели – такой модели, коэффициенты ПФ которой постоянно корректируются.
Решим задачу для конкретной ПФ второго порядка:
(15)
С целью нахождения модели объекта введем в рассмотрение полином на 1 меньше, характеризующийся с известными полюсами, которые являются отрицательными, простыми и вещественными, т.е. многочлен должен быть устойчивым.
Разделим числитель и знаменатель ПФ на данный многочлен:
.
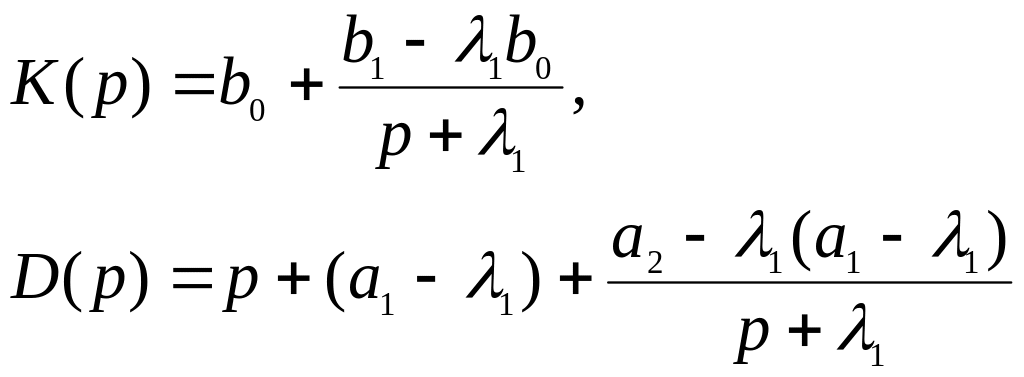Обозначим
.
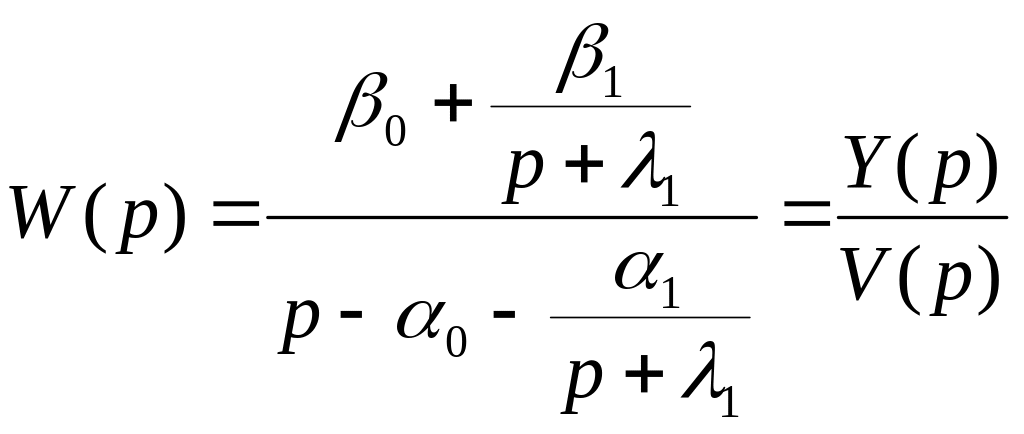(16)
От описания системы с помощью ПФ переходим к описанию в терминах Лапласа:
(16а)
Заменим
переходим к операторной форме записи:
(16б)
Разрешим (16б) относительно выхода объекта:
(17)
На основании (17) создается модель объекта (17а):
(17а)
Задача:
определить коэффициенты
.
Для этого введем в рассмотрение
погрешность
идентификации:
.
.
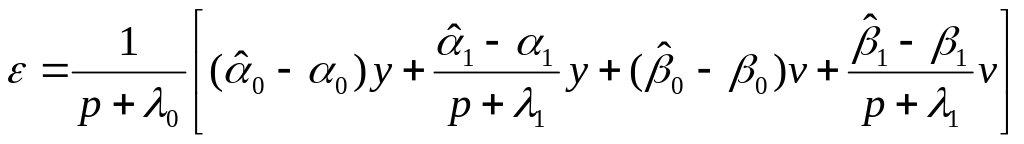Критерий
идентификации:
.
Коэффициенты модели следует подбирать такими, чтобы в каждый момент времени критерий идентификации достигал бы минимума.
Для решения задачи используется градиентный метод:
.
Вектор
производных коэффициентов определяется
в виде поправки, где
– известная величина,
– градиент критерия идентификации:
.
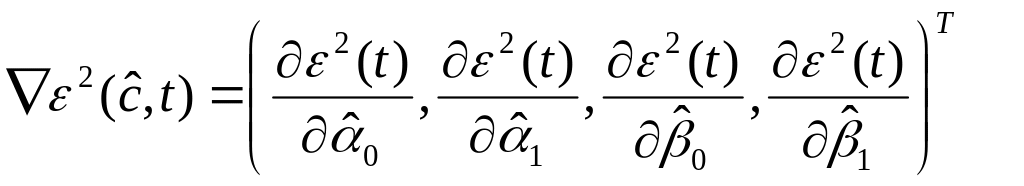Каждый из четырех компонентов вектора производных оценок определяется:
Вычислим
производные от критерия идентификации
по всем
.
Полученные для производных оценок
коэффициентов:
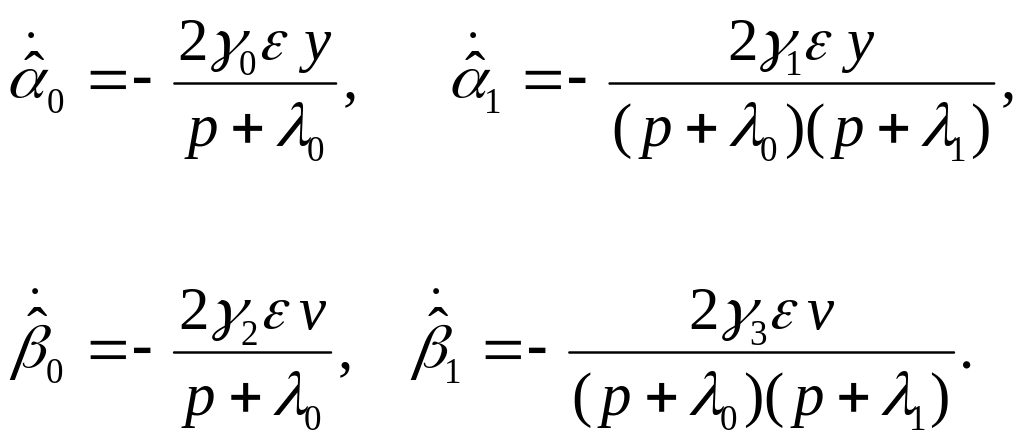
Проинтегрируем обе части каждого из выражений и найдем оценки соответствия
коэффициентов:
где
– оператор дифференцирования.
Таким образом, коэффициенты находятся на основании ошибки и выхода, ошибки и входа.
Рассмотрим формирование выхода модели. Схема строится на основании (17а).
v(t)
y(t)
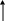
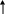
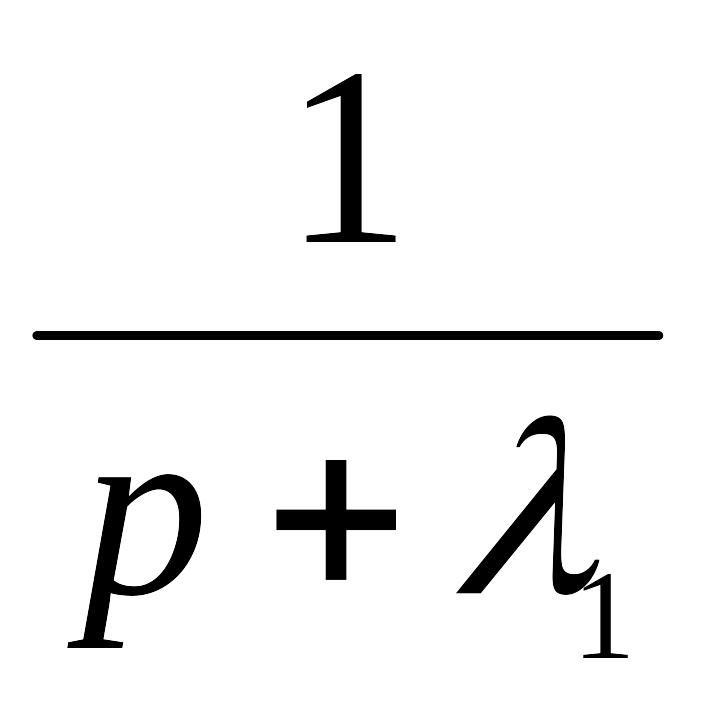
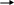
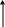
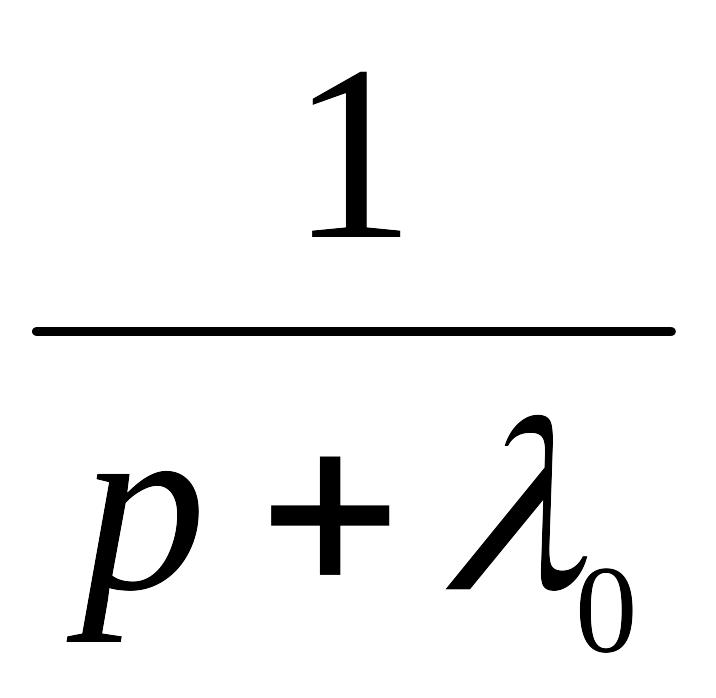
Схема
формирования оценки
.
ε(t)
v(t)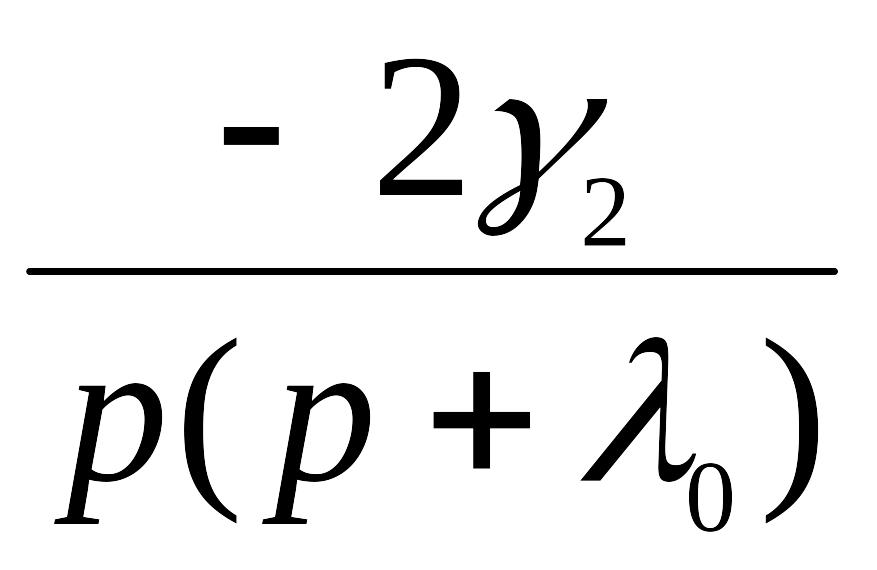
Схема
формирования оценки
.
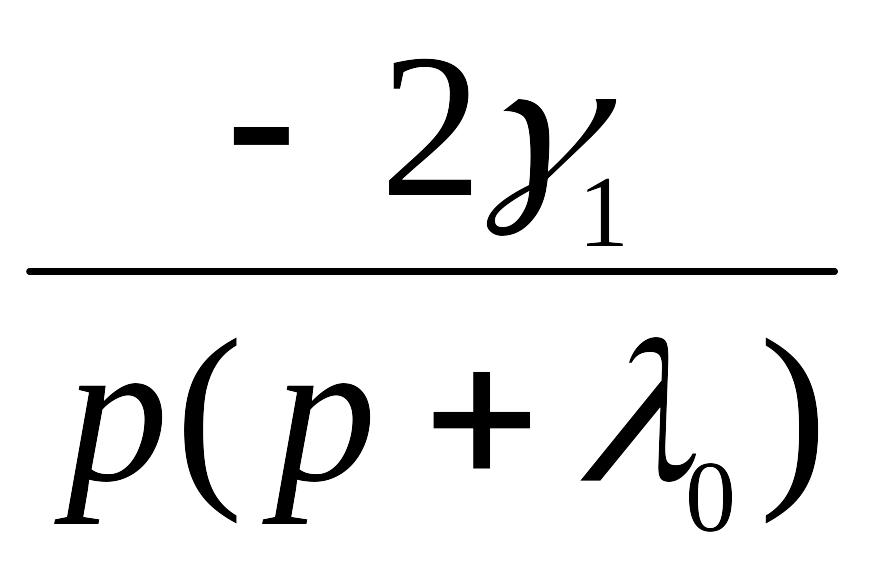
y(t)
ε(t)
Схема для ПФ второго порядка:
Метод модулирующих функций
Применяется, когда ОУ с одним входом и одним выходом описывается дифференциальным уравнением (дифференциальной моделью). Предположим, что выбрана одна из множества дифференциальных моделей – модель n – го порядка вида:
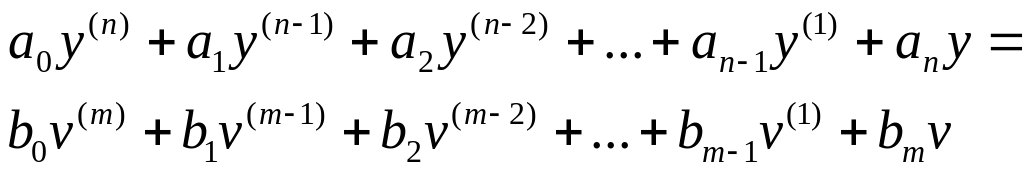(1а)
(1б)
На основании априорных сведений известна структура объекта (известен порядок левой и правой части ДУ)
В уравнении (1а) и (1б):
Модель
(1а) описывается физически реализуемым
ОУ.
Введем
обозначения для производных
.
Представим (1а) в виде (1в), т.е. свяжем выход объекта с его входом.
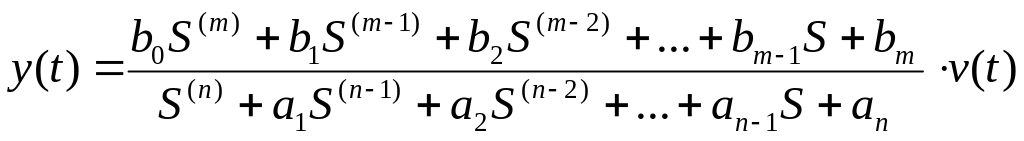(1в)
В
соответствии с (1в) построим модель вида
(1г), где
– оценка выхода объекта (выход модели),
коэффициент
– оценок ДУ.
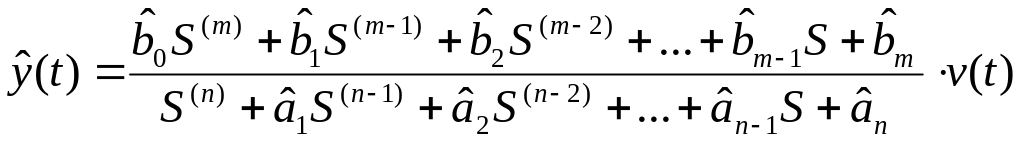(1г)
Задача
заключается в нахождении оценок
коэффициентов
по
результатам измерений
.
Входы и выходы являются случайными процессами, т.е. в них присутствуют помехи, мешающие наблюдениям. Для решения задачи необходимо (в соответствии с (1а)) использовать не только наблюдаемые входы и выходы, но и их производные до порядка m и n. Т.к. и входы и выходы содержат случайные составляющие, их дифференциация (даже однократная) приводит к большим ошибкам. Кроме того, операция дифференцирования является физически неосуществимой, и следовательно, нужно использовать приближенную дифференциацию. Что приводит к еще большим ошибкам. Поэтому используется другой способ решения задачи.
Задается
система линейно независимых функций
,
,
(не меньше числа оцениваемых коэффициентов
ОУ), называемых модулирующими
и обладающих свойствами:
(2)существуют все n производных на интервале
.
Предположим, что выбрали все k функций. Умножим обе части (1б) на функции с последующим интегрированием в пределах .
(3)
.
В результате перемножения на моделирующие функции увеличивается число соотношений (n+m+1).
Умножение на моделирующую функцию и интегрирование осуществляется, чтобы освободить от производных выходы и входы. Рассмотрим вначале интегралы, которые не содержат производных входа и выхода объекта:
,
.
Далее интегралы, содержащие производные входа и выхода объекта. Первый из них:
интегрируем по частям, используя условие (2):
