Идентифицируемость оу

Рассмотрим автономную динамическую систему, которая описывается моделью в переменных состояниях

(1)

Определить: При каких условиях можно измерить матрицу динамики , если объект наблю­даем и все его состояния измеримы.

Решение.

Перейдем к дискретному времени, так как состояния измеряются в дискретные моменты времени.

– допредельные значения.

Получим: (2)

Дискретная модель представлена разностными уравнениями состояния.

Так как объект автономный, то он совершает движения под воздействием ненулевых начальных условий. Измеряем состояния:

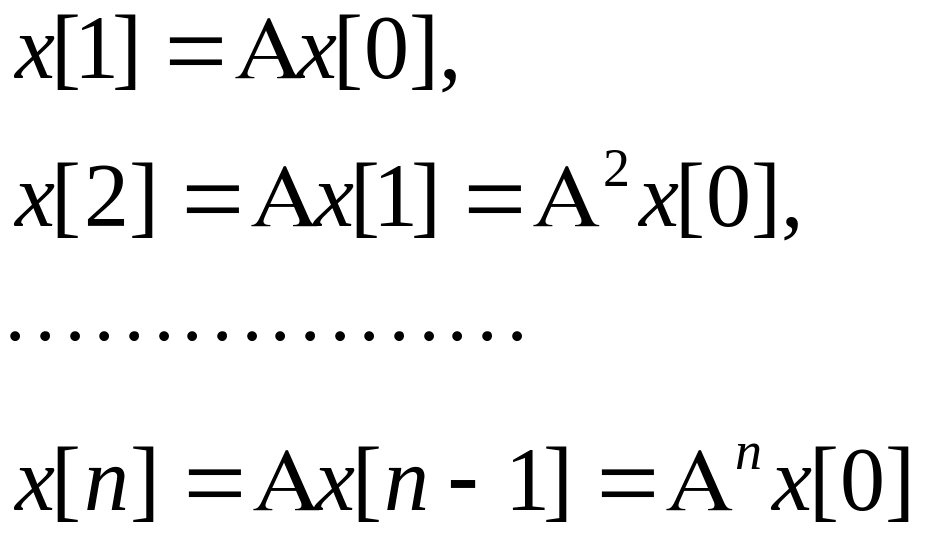
Совокупность измерений состояний записывается в матричном виде:

(3)

Правый сомножитель (3) обозначим через B:

-

Объект называется идентифицируемым, если матрица B – неособенная матрица (условие идентифицируемости).

(Если это так, то из (3) следует оценка матрицы динамики:

(4)

Условие идентифицируемости позволяет оценивать элементы матрицы динамики А.

Оценка состояний объекта

Объект описывается моделью переменных состояния:

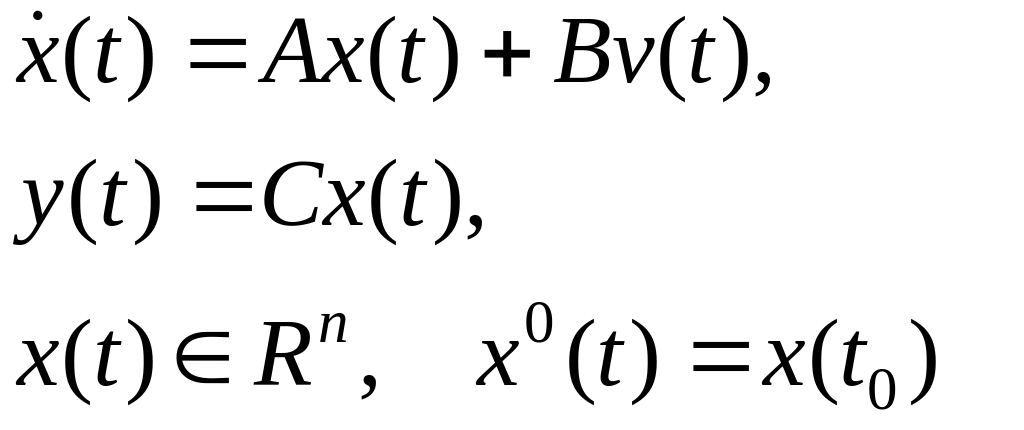
Чтобы осуществить идентификацию необходимо определить элементы матриц A, B, C. Необходимо иметь наблюдения за выходом и данные о состоянии объекта в различные моменты времени. Не все переменные состояния измеримы.

Возникает задача оценки состояний объекта по измеряемому выходу. В результате наблюдений за объектом с одним входом и выходом в дискретные моменты времени получаем массивы данных о входе/выходе объекта. Требуется найти способ измерения состояний объекта.

Решение:

Переходим к дискретному времени. Непрерывные объекты описываются разностными уравнениями движения:

– уравнение состояния.

– уравнение выхода.

.

При наблюдении за выходом объекта установлено, что на конечном интервале наблюдений выходной сигнал представляется в виде ряда Тейлора с n элементами. Разложим выходной сигнал на интервалы в ряд Тейлора в окружности текущих наблюдений t.

(6)

Разложение (6), которое примерно описывает выход объекта будем считать моделью выходного сигнала.

Осуществим переход к дискретному времени

– период дискретизации, m – текущее дискретное наблюдение выхода

В результате (6) (7):

(7)

введем в рассмотрение оценку векторов состояний объекта

m- компонент из выхода u (m-1) производных.

Модель (7) запишем в (8):

(8)

– элементами вектора являются соответствующие коэффициенты правой части (7).

Выход объекта и модель выходного сигнала отличаются друг от друга ошибкой идентификации. Выход можно выразить через модель и ошибку идентификации:

Если , – память фильтра, то данное соотношение можно записать в развернутой форме для всех значений :

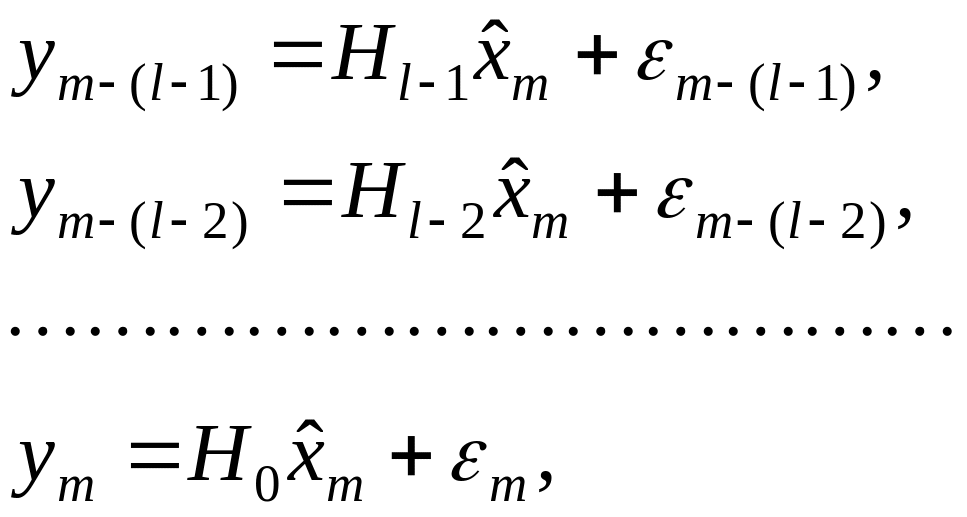
Систему из соотношений можно записать в векторной форме (9):

(9)

где

– вектор измеренных значений выхода на интервале величиной .

– вектор ошибки идентификации.

– блочная матрица коэффициентов, число строк равно памяти фильтра.

Для упрощения будем считать, что ошибки идентификации – белый дискретный шум, т.е. их значения некоррелированны.

Находим вектор ошибки идентификации:

Составим квадратичный критерий идентификации и оценку состояния объекта выбираем такой, чтобы критерий идентификации стремился к минимуму:

(10)

В результате приходим к оптимизации задачи (10) – нахождения векторного произведения по оценке и приравниваем её к нулевому вектору:

Решая последнее уравнение относительно оценки, получаем ее значение:

(11)

Оценка состояний объекта является МНК – оценкой, которое получается на основе анализа выхода объекта (11) описываем фильтр с конечной памятью. Память = .

Пока память фильтра не заполнена данными. Он находится в переходном режиме

0

Происходит выталкивание последнего элемента и заполнение следующим.