
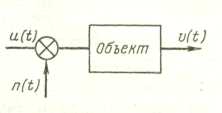
- •Идентификация как метод построения моделей
- •Задача идентификации
- •Сведения об объекте.
- •Идентификация статических оу. Определение статического объекта
- •Регрессионные модели идентификации
- •Выбор уравнения регрессии
- •Оценка параметров линейной регрессионной модели (пассивный эксперимент).
- •Аппаратная реализация процесса идентификации
- •Оценка адекватности модели
- •Проверка центрированности остаточного ряда
- •Проверка остатков на нормальное распределение
- •Оценка значимости модели и ее параметров
- •Критерий Фишера
- •Ошибка аппроксимации
- •Нелинейные регрессионные модели
- •1. Метод покоординатной оптимизации (Гаусса – Зайделя).
- •Градиентные методы поиска
- •Метод сопряженных направлений
- •Метод Ньютона
- •Квазиньютоновские методы
- •Динамические детерминированные су Линейные динамические объекты
- •Частотный метод определения коэффициентов пф
- •Идентификация с помощью настраиваемой модели
- •Метод модулирующих функций
- •В общем случае получаем
- •Конструкция модулирующих функций
- •Применение дискретных моделей для идентификации непрерывного оу
- •Непараметрические модели идентификации
- •Корреляционный метод идентификации
- •Корреляционный метод, решаемый на эвм
- •Разделим обе части (8) на :
- •Идентифицируемость оу
- •Оценка состояний объекта
- •Аппроксимация весовой функции оу
- •Авторегрессионные модели динамических объектов
- •Выбор периода дискретизации
- •Идентификация нелинейных непрерывных оу
- •Модели линейные относительно идентифицируемых параметров
- •Или более компактно, введя реакции динамических звеньев (5):
- •Представим степень интеграла в правой части (23) в виде произведения интегралов:
- •Планирование эксперимента
- •Критерии планирования эксперимента
- •Планы для моделей, описываемых полиномами первого порядка
- •Информационная матрица плана:
- •Полные факторные планы
- •Правило построения полных факторных планов
- •Дробные факторные планы (дробный факторный эксперимент)
- •Свойства полных и дробных факторных планов для линейных моделей
- •Технология проведения эксперимента
- •Планы второго порядка
- •Ротатабельный ортогональный центральный композиционный план
- •Диагностика линейных оу методом комплиментарного сигнала.
- •Аналитический расчет кс
- •Расчет кс по измеренным значениям выходного сигнала
- •Процедуры диагностирования
- •Локализация дефектов по годографу неисправностей (гн)
- •Байесовский метод диагностики
- •Прогнозирование технического состояния.
- •Линейное прогнозирование
Разделим обе части (8) на :
![]() (9)
(9)
Весовую
функцию будем определять исходя из
минимума суммы квадратов отклонений
выхода модели относительно выхода ОУ
![]() (квадратичного критерия).
(квадратичного критерия).
 (10)
(10)
Требуется подобрать такие дискреты, чтобы критерий идентификации достигал бы минимума. Берутся частные производные и приравниваются к нулю.

Преобразуем последнее выражение и разделим обе части на N-m, N – число измерений входа и выхода в моменты времени, отстоящие друг от друга на период дискретизации .
![]() (11)
(11)
Вторая
сумма в правой части – коэффициенты
корреляции между сдвинутыми на (i-
j)
тактов выборками входного сигнала
![]() :
:
![]()
![]()
а через i – коэффициенты взаимной корреляции между входом и выходом ОУ:
![]() .
.
Таким образом дискретный вариант уравнения Винера-Хопфа – (12):
![]() (12)
(12)
Введем
в рассмотрение векторное значение
весовой функции
![]() .
.
Корреляционной
матрицей входа
![]() ,
составленной из коэффициентов корреляции
входов и вектор взаимной корреляции.
Тогда система уравнений (12) можно
записать в векторной форме (13):
,
составленной из коэффициентов корреляции
входов и вектор взаимной корреляции.
Тогда система уравнений (12) можно
записать в векторной форме (13):
![]() (13)
(13)
Откуда находится вектор значений весовой функции объекта:
![]() (14)
(14)
(14) показывает, что задача может быть решена, если корреляционная матрица входа является невырожденной и если эта матрица является хорошо обусловленной, а задача идентификации в этом случае корректно поставлена.
Если найти все собственные числа корреляционной матрицы входа, определяем среди них максимальное и минимальное, найдем отношение максимального и минимального, то полученное число – обусловленностей этой матрицы. Если число обусловленностей не сильно отличается от 1, то корреляционная матрица называется хорошо обусловленной. Хорошо обусловленная корреляционная матрица делает задачу идентификации корректной.
Задача идентификации считается корректно поставленной, если решение (3) и (13) существует при заданных корреляционных функциях, это решение единственное и устойчивое. Решение устойчиво, т.е. бесконечно малым вариациям исходных данных соответствуют бесконечно малые вариации решения.
Величина заданной идентификации является некорректной, то в результате решения (3) и (13) получается следующая весовая функция:

![]() -весовая
функция объекта
-весовая
функция объекта
Простейшим методом, обеспечивающим корректность задачи, является регуляризация. В критерий идентификации добавляется дополнительное слагаемое с коэффициентом регуляризации :

И ищутся дискреты весовой функции, которые обращают критерий в минимум. Введение этого слагаемого делает задачу корректной, но решение, получаемое, имеет тенденцию смещения к оси абсцисс.

Можно использовать другие слагаемые, которые оказывают сглаживающее действие (рис.б).

Выбирая число отсчетов весовой функции m на интервале наблюдений (переходного процесса). Эта величина определяется по теореме Котельникова.
![]() ,
,
где
![]() – максимальная частота спектра весовой
функции
– максимальная частота спектра весовой
функции
![]() ,
которую
можно приближенно определить из
условия
,
которую
можно приближенно определить из
условия
![]()
Аналитический анализ показывает, что при этих предположениях число m не превышает m = 22.
Пример.
Проиллюстрируем
эффект регуляризации в задаче
определения весовой функции объекта
![]() .
.
Пусть
корреляционная функция входа объекта
имеет вид:
![]() .
.

Рис. Поведение весовой функции объекта w(t) и ее оценок.
Если
входной сигнал объекта является белым
шумом, корреляционная функция которого
содержит
![]() функцию:
функцию:
![]() .
.
то выражение (3) принимает вид:
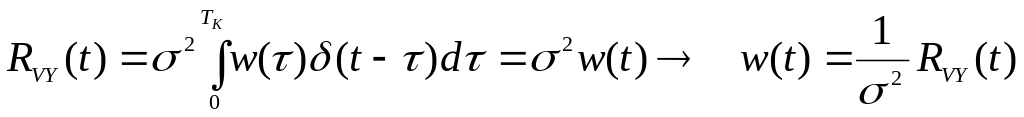
Оценка весовой функции пропорциональна взаимной корреляционной функции входа/выхода. Это свойство можно использовать на практике, если ко входным воздействиям подмешивать белый шум, некоррелированный со входом :
![]() .
.
Тогда на основе интеграла свертки:
![]() ,
,
Обе части умножаем на смещенный белый шум и подвергаем операции математического ожидания:
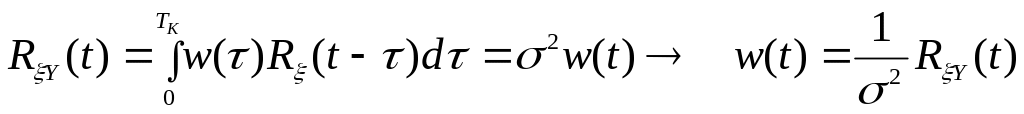
 .
.
Существует телеграфный сигнал
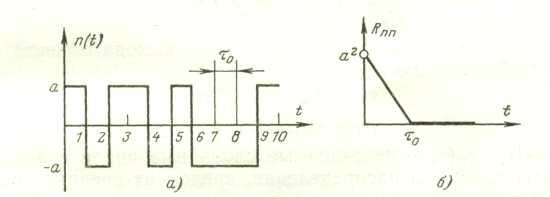
Этот си Сигнал можно использовать в качестве входного воздействия.
