§2. Простейшие теоремы теории вероятностей

Определение: Суммой С = А + В двух событий А и В называется событие С, состоящее в появлении хотя бы одного из событий А или В.

Теорема 1. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, т.е.

(А3)

Р(А+В)=Р(А)+Р(В)

Доказательство проведем для событий, составляющих схему случаев.

Пусть возможные исходы опыта сводятся к совокупности случаев, которые мы для наглядности изобразим в виде n точек.

Предположим, что из n случаев m благоприятны событию А, а k — событию В. Тогда

(А4)

Так как события А и В несовместны по условию теоремы, то нет таких случаев, которые благоприятны и А, и В вместе. Следовательно, событию А + В благоприятны m + k случаев и

(А5)

Подставляя (А4) и (А5) в (АЗ), получим тождество, что доказывает теорему.

Теорему сложения вероятностей, доказанную для двух событий, легко по индукции распространить на любое число несовместных событий:

P(A₁ + А₂ + ... + А_n) = Р(А₁) + Р(А₂) + ... + Р(А_n)

или

(А6)

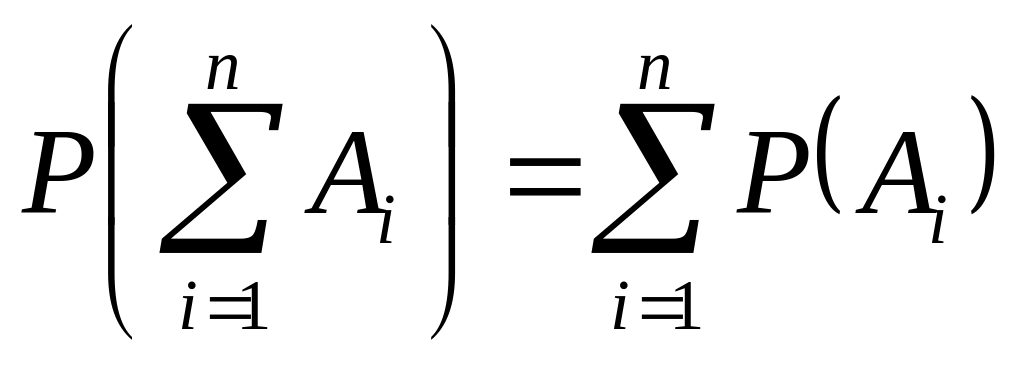
Следствие 1. Если события А₁, ..., А_n образуют полную группу несовместимых событий, то сумма их вероятностей равна единице

(А7)

Доказательство. Так как событие А₁, ..., А_n образуют полную группу, то появление в опыте хотя бы одного из них — достоверное событие

(А8)

P(A₁ + А₂ + ... + А_n) =1

Так как А₁, ..., А_n по условию несовместны, то к ним применима теорема сложения вероятностей:

(А9)

P(A₁ + А₂ + ... + А_n) = Р(А₁) + Р(А₂) + ... + Р(А_n)=

Из (А8) и (А9) следует, что

Определение. Противоположными событиями и называют два несовместных события, образующих полную группу.

Сумма вероятностей противоположных событий, на основании следствия 1, очевидно, равна единице, т.е.

(А10)

Определение. Событие А называют независимым от события В, если вероятность события А не зависит от того произошло событие В или нет, т.е.

(А11)

Р(А/В) = Р(А)

В выражении (А11) Р(А/В) — есть вероятность события А при условии, что событие В имело место. Говорят, что Р(А/В) условная вероятность события А.

Пример: Пусть в урне имеется 3 белых и два чёрных шара. Два лица вынимают из урны по одному шару. Рассмотрим два события:

А — появление белого шара у 1-го лица.

В — появление белого шара у 2-го лица.

Вероятность события А до того, как известно что-либо о событии В, равна 3/5. Если стало известно, что событие В произошло, то вероятность события А становиться равной 1/2, из чего заключаем, что событие А зависит от события В.

Определение. Произведением двух событий А и В называется событие состоящее в совместном (или одновременном) появлении этих двух событий.

Теорема 2. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие имело место:

(А12)

Р(А, В) = Р(А)Р(В/А)

Докажем теорему 2 для событий, сводящихся к схеме случаев. Пусть возможные исходы опыта сводятся к n случаям, которые изобразим в виде точек

Предположим, что событию А благоприятны m случаев, а событию В благоприятны k случаев. Так как по условию теоремы не предполагается, что события А и В несовместны, то вообще говоря существуют случаи, благоприятные и событию А, и событию В одновременно. Пусть число таких случаев l. Тогда

(А13)

Вычислим Р(В/А), т. е. условную вероятность события B в предположении, что А имело место. Если известно, что событие А произошло, то из ранее возможных n случаев остаются возможными только те m случаев, которые благоприятствовали событию А. Из них l случаев благоприятны событию В. Поэтому

(А14)

Подставляя (А13) и (А14) в (А12) получим тождество. Теорема доказана.

Следствие 1. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.

Следствие 1 непосредственно вытекает из определения независимости событий Р(В/А)=Р(В) и теоремы 2.