Глава1. Некоторые понятия молекулярной физики

§1 Массы атомов и молекул. Молярная масса

Так как массы атомов и молекул чрезвычайно малы (10^–25 – 10^–27 кг), то их удобно измерять не в килограммах, а в специальных относительных единицах. В качестве единичной атомной массы m_ед принимается двенадцатая часть массы изотопа углерода ¹²С. Измерения этой величины дали следующее значение:

(1)

Относительной атомной единицей массы А_r называется отношение массы данного атома m_ат к атомной единице массы m_ед, т. е.

(2)

Величины А_r для химических элементов приведены в таблице Менделеева.

Относительная молекулярная масса молекулы M_r определяется по аналогичной формуле:

(3)

Относительные молекулярные массы с достаточной точностью могут быть найдены в виде суммы относительных атомных масс, составляющих молекулу. Зная M_r для данной молекулы, легко найти её массу

(4)

В системе единиц СИ количество вещества выражается в молях. Молем называют количество вещества, содержащее столько частиц (молекул, атомов, электронов, фотонов и т.д.), сколько атомов содержится в 12г изотопа углерода ¹²C. Это число называют постоянной Авогадро N_A. Согласно определению

(5)

Учтя (1), получим

(6)

Массу одного моля называют молярной массой. Очевидно, что

(7)

С учетом (3) и (5), выражение (7) примет вид

(8)

Число  молей связано с числом N молекул, содержащихся в данном количестве вещества, соотношением

(9)

Умножив числитель и знаменатель выражения (9) на массу m_мол молекулы, получим

(10)

§2. Молекулярные силы

Силы, действующие между молекулами, по своей природе являются силами электрическими. Молекула состоит из положительно заряженных ядер атомов, составляющих молекулу, и отрицательно заряженных электронных оболочек атомов. Поэтому при взаимодействии молекул одновременно действуют как силы притяжения разноименных зарядов, так и силы отталкивания одноименных. И те и другие с увеличением расстояния между центрами масс молекул быстро уменьшаются. Однако убывание сил отталкивания оказывается более быстрым, чем сил притяжения, в результате чего оказывается, что силы отталкивания преобладают на весьма малых расстояниях между молекулами, а силы притяжения ― на более дальних расстояниях, однако и они довольно быстро убывают с расстоянием. Качественно это можно объяснить так.

При расстоянии между молекулами значительно большем их диаметра (рис. 1.а), молекулы практически не взаимодействуют, так как вращающиеся вокруг ядер электроны полностью компенсируют заряды этих ядер и молекулы в целом электрически нейтральны. (При этом электрическое поле нейтральной молекулы, вообще говоря, полностью не исчезает, но оно очень быстро убывает за пределами молекулы. Практически оно равно нулю на расстояниях двух-трёх диаметров молекулы.)

П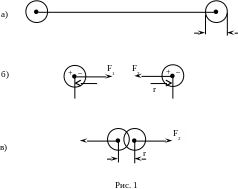 ри дальнейшем сближении двух молекул (рис.1,б) начинает постепенно проявляться взаимодействие электрических зарядов ядер и электронных оболочек молекул. Это происходит из-за притяжения разноимённых и отталкивания одноимённых зарядов. Произойдёт небольшая деформация (поляризация) обеих взаимодействующих молекул, как это показано на рис. 1,б. В результате между молекулами возникнут силы притяжения.

По мере дальнейшего сближения деформация молекул и величина сил притяжения будут возрастать. Однако, когда молекулы подойдут «вплотную» друг к другу и «соприкоснутся» своими электронными оболочками, то дальнейшее сближение окажется «практически» невозможным. Между электронными оболочками возникнут огромные силы отталкивания, резко возрастающие по мере дальнейшего взаимного проникновения оболочек. На таких расстояниях будут преобладать силы отталкивания (рис. 1,в).

Абсолютная величина сил взаимодействия существенно зависит от конкретного строения молекул. Кроме того, для несферических молекул силы взаимодействия зависят, очевидно, не только от расстояния r между центрами масс молекул, но и от взаимной ориентации молекул. Однако общий характер зависимости силы взаимодействия от расстояния одинаков ― притяжение на больших расстояниях и отталкивание на малых.

Рис. 2

На рис. 2,а,б приведены зависимости сил отталкивания, которые в физике положительны (F₁>0), и сил притяжения (F₂<0) от расстояния r между молекулами. Эти силы действуют одновременно. Поэтому, чтобы найти результирующую, их нужно сложить. Если сложить ординаты положительной быстро падающей силы отталкивания F₁ с отрицательными ординатами медленно растущей силы притяжения F₂, то результирующая функция F=F₁+F₂ будет иметь вид, показанный на рис. 2,в.

Как видим из рис.2,в, на расстояниях r < r₀ между молекулами преобладают силы отталкивания, а при r > r₀ ― силы притяжения, при эти силы равны. Как известно из механики, сила F связана с потенциальной энергией E_p соотношением

(11)

На рис.2,г приведена проинтегрированная функция F(r), т. е. потенциальная энергия E_p взаимодействия молекул как функция расстояния r. Из рисунка видно, что потенциальная энергия при r = r₀ принимает минимальное значение E_p0. Точка r = r_o является точкой устойчивого равновесия взаимодействующих молекул (в этой точке сила ).

Из теории и опыта следует, что потенциальная энергия взаимодействия молекул E_p(r) хорошо описывается функцией вида:

(12)

,

где a₁ и a₂ положительные постоянные. Первый член соответствует силам отталкивания, второй ― силам притяжения. Величина показателя n степени зависит от структуры молекулы и находится в пределах 8≤ n ≤ 15. Как видно из формулы (12), силы притяжения, хотя и медленнее (r ^–7), чем силы отталкивания (r ^–n+1) убывают с ростом r, но, как показывают расчеты, и они на расстояниях ρ>10 ^–9 м между молекулами оказываются пренебрежимо малыми. Поэтому сферу с радиусом ρ10 ^–9 м называют сферой молекулярного действия сил. На расстояниях ρ>10 ^–9 м силу взаимодействия между молекулами полагают равной нулю.

Приведем в качестве иллюстрации известные из теории и опыта эффективные диаметры d некоторых молекул

Таблица 1.

Молекула	H2	He	O2	N2	CO2
d, 10 –10 м	2,74	2,18	3,61	3,75	4,65

Как видно из таблицы, силами притяжения можно пренебречь уже на расстояниях в несколько диаметров молекул.