§5. Адиабатический процесс. Уравнение адиабаты идеального газа. Работа идеального газа при адиабатическом изменении его объема.

Адиабатическим называется процесс, происходящий без теплообмена с внешней средой. В отличие от изотермического процесса, требующего хорошего теплового контакта тела со средой, адиабатический процесс, напротив, требует хорошей тепловой изоляции тела от окружающей среды. Для адиабатического протекания процесса тело должно быть заключено в совершенно нетеплопроводную или адиабатическую оболочку. адиабатическая оболочка является физической абстракцией. В действительности таких оболочек не существует, но можно создать оболочки, приближающиеся по своим свойствам к адиабатическим. Наиболее совершенными адиабатическими оболочками в современной физике и технике являются стенки сосудов Дьюара или термосов. Это стеклянные или металлические баллоны с двойными стенками, между которыми создан высокий вакуум. Они хорошо предохраняют помещаемые в них тела от теплообмена с внешними телами. Если в сосуде Дьюара производить изменение объема какого-либо тела (например, газа), то такой процесс можно считать адиабатическим. Близкими к адиабатическим являются также процессы, протекающие настолько быстро, что обмен тепло с внешними телами не успевает осуществляться в сколько-нибудь заметных количествах. Примером адиабатического процесса может служить расширение газа при истечении его из камеры реактивного двигателя. Близкими к адиабатическим являются процессы расширения и сжатия рабочего вещества в двигателях внутреннего сгорания. Адиабатическими можно считать также сжатия и расширения, происходящие в каждой точке газа, в котором распространяется звуковая волна.

Математически адиабатический характер процесса выражается в том, что в относящихся к этому процессу уравнениях термодинамики следует полагать δQ = 0 и Q = 0. поэтому первое начало термодинамики в применении к адиабатическому процессу принимает вид

(119)

или

(120)

Равенство (120) показывает, что при адиабатическом процессе работа δA может производиться только за счет изменения внутренней энергии тела. Если тело совершает положительную работу (δA>0), то его внутренняя энергия убывает (dU <0). Если же внешние силы совершают над телом работу (δA<0), то внутренняя энергия тела возрастает (dU >0).

В случае идеального газа внутренняя энергия зависит только от температуры и равна

(121)

где ― молярная теплоемкость газа при постоянном объеме. Изменение внутренней энергии идеального газа означает, следовательно, изменение его температуры

(122)

Подставляя в (119) это значение dU, а также вместо δA его выражение через изменение объема δA = PdV, запишем первое начало термодинамики в применении к адиабатическому процессу в идеальном газе в виде

(123)

Из уравнения (123) видно, что при адиабатическом расширении ( ) газ охлаждается (dT <0), а при адиабатическом сжатии ( ) газ нагревается (dT >0).

С изменением температуры газа при адиабатическом изменении его объема приходится часто встречаться в технике и это явление хорошо используется на практике. В частности, адиабатическое нагревание газа используется в двигателях внутреннего сгорания дизельного типа. всасываемый в рабочие цилиндры двигателя воздух адиабатически сжимается настолько, что его температура повышается до 600º C, после чего подаваемое в цилиндры горючее воспламеняется от одного соприкосновения с нагретым воздухом. Адиабатическое охлаждение газа при его расширении с совершением внешней работы используется в холодильной технике, в частности, в современной технике сжижения газов.

Для вычисления работы, совершаемой газом при адиабатическом изменении его объема, необходимо знать соотношение между давлением газа и его объемом при этом процессе, т. е. необходимо знать уравнение адиабатического процесса в переменных P, V. При адиабатическом процессе закон Бойля-Мариота уже несправедлив, так как при этом процессе изменяется температура газа. Для отыскания соотношения между давлением и объемом идеального газа при адиабатическом процессе будем исходить из уравнения (123), выражающего первое начало термодинамики, примененное к адиабатическому процессу в идеальном газе. Исключим из уравнения (123) величину dT. Для этого воспользуемся уравнением состояния газа

(124)

Дифференцируя это уравнение, получаем

откуда

Подставляя это выражение в (123), находим

или

Переписав последнее уравнение в виде

и принимая во внимание, что , то получаем

Разделяя в этом уравнении переменные, преобразуем его к виду

(125)

Введем обозначение , тогда

(126)

Уравнение (126) представляет собой дифференциальное уравнение адиабатического процесса для идеального газа. Теплоемкости C_p и C_v газов могут зависеть от температуры. Однако, во многих случаях эти величины в довольно широких температурных интервалах остаются постоянными. В этих случаях постоянно также и их отношение γ и уравнение (126) легко интегрируется. В результате интегрирования, получаем

или

Так как величина, логарифм которой постоянен, также постоянна, то

(127)

Уравнение (127) и дает нам искомое соотношение между давлением и объемом идеального газа при адиабатическом процессе. Оно называется уравнением адиабаты идеального газа или уравнением Пуассона, а величина называется показателем адиабаты. Так как C_p>C_v, то γ >1, поэтому кривая зависимости давления от объема при адиабатическом процессе, называемая адиабатой, является более крутой, чем изотерма . Если через произвольную точку 1 на графике P, V изображающую некоторое состояние идеального, провести его изотерму и адиабату, то эти кривые будут иметь вид, представленный на рис.12. Более крутое падение давления с увеличением объема при адиабатическом процессе обусловлено тем, что при адиабатическом р асширении газа его давление уменьшается не только за счет увеличения объема, но и вследствие происходящего при этом понижения температуры. Если, исходя из состояния 1, газ начать расширять адиабатически, то его температура начнет понижаться, в результате чего давление будет уменьшаться сильнее, чем при изотермическом расширении. Поэтому адиабатическое расширение изображается участком кривой 1B', идущим вниз круче, чем ветвь изотермы 1B. Если же, исходя из состояния 1, газ начать сжимать адиабатически, то его температура начнет повышаться, благодаря чему давление P будет возрастать сильнее, чем при изотермическом сжатии, и адиабатическое сжатие изображается участком 1A', идущим вверх круче, чем участок изотермы 1A.

Пользуясь уравнением Пуассона (127) и уравнением состояния идеального газа (124), можно найти соотношение между другими параметрами газа при адиабатическом процессе, т. е. получить уравнение адиабаты идеального газа в других переменных. Так, исключив из (127) с помощью уравнения (124) давление P, получим соотношение между температурой газа и его объемом при адиабатическом процессе. Подставляя в (127) значение , получаем или

(128)

Поскольку νR ― величина постоянная для данной массы газа, формула (128) представляет собой уравнение адиабаты идеального газа переменных T, V.

Точно также, исключая из уравнений (127) и (124) объем V, найдем уравнение адиабаты идеального газа в переменных T, P. Из уравнения состояния имеем . Подставляя это значение в (127), получаем

,

Возводя обе части последнего равенства в степень , находим

(129)

Пользуясь полученным уравнением адиабаты (127), можно теперь вычислить работу, совершаемую идеальным газом при его адиабатическом расширении (или работу, производимую внешними силами при адиабатическом сжатии газа). Запишем уравнение адиабаты (127) в виде

(130)

где P₁ ― начальное давление газа, а V₁ ― его начальный объем. Выразим из (130) давление газа через его объем и значения параметров в начальном состоянии

Подставляя это значение P в общую формулу для работы, получаем

(131)

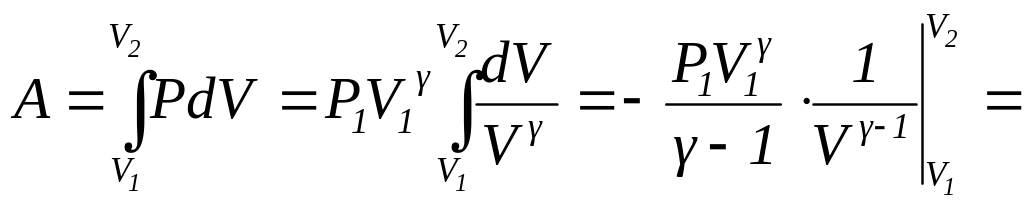
Так как , то

(132)

Легко видеть, что при расширении газа из начального состояния P₁, V₁ (или T₁, V₁) до некоторого другого объема V₂ работа при адиабатическом процессе меньше, чем при изотермическом. Это хорошо видно из графика зависимости давления от объема P =P(V) при этих процессах (рис. 12). На этом графике работа, совершаемая при адиабатическом расширении от объема V₁ до объема V₂, выражается площадью под участком адиабаты 1C', а работа при изотермическом расширении ― площадью под участком 1C. Наоборот, при адиабатическом сжатии газа придется затратить большую работу, чем при изотермическом сжатии на ту же величину, если исходить из одинаковых начальных условий, что также видно из рис.12.