§4. Изотермический процесс. Работа идеального газа при изотермическом изменении его объема

Изменение объема газа, т.е. его расширение или сжатие, можно произвести так, чтобы температура газа оставалась постоянной. Такой процесс изменения состояния газа или другой системы, который проходит при постоянной температуре, называется изотермическим. Для того чтобы процесс в системе мог протекать изотермически, она должна быть помещена в среду с постоянной температурой, к примеру, в термостат — аппарат, в котором специальное устройство — терморегулятор — автоматически поддерживает температуру постоянной. Расширяясь в термостате, т.е. при T=const, система производит некоторую работу, которая по первому началу термодинамики равна:

(109)

где ― количество теплоты, поглощенной системой от термостата, а ― изменение ее внутренней энергии.

В случае идеального газа внутренняя энергия зависит только от температуры и не зависит от занимаемого им объема. Поэтому при изотермическом расширении или сжатии идеального газа его внутренняя энергия остается неизменной при и . Первое начало термодинамики (109) в этом случае принимает вид:

(110)

(111)

A=Q

Это равенство показывает, что при изотермическом расширении объема идеального газа работа может производится только за счет поглощаемого им тепла . Если газ изотермически расширяется ( ), то он совершает положительную работу ( ) и согласно равенству (110) получает извне (от среды термостата) такое же количество тепла ( ). Если же внешние силы совершают над газом работу при его изотермическом сжатии ( , ), то он отдает такое же количество тепла ( ). Таким образом, в случае изотермического расширения газ полностью преобразует подводимое к нему тепло в совершаемую работу. Наоборот, при изотермическом сжатии работа, затраченная на сжатие, полностью преобразуется в отдаваемое газом внешней среде (среде термостата) тепло. Именно по этой причине внутренняя энергия и температура газа остаются неизменными. Газ при изотермическом процессе ведет себя как тело с бесконечно большой теплоемкостью. Математически это следует из общего определения теплоемкости; обозначив изотермическую теплоемкость через С_Т, получаем

, т. к. ,

Из сказанного выше ясно, что для того, чтобы расширение газа могло происходить изотермически, ему необходимо непрерывно передавать тепло извне. Наоборот, чтобы сжатие газа протекало изотермически, от него необходимо непрерывно отбирать тепло. Изотермический процесс, следовательно, возможен лишь при идеально хорошем обмене теплом между газом и внешней средой (средой термостата). Практически приблизиться к изотермическому процессу можно, заставляя протекать его настолько медленно, чтобы температура газа все время успевала выравниваться с температурой окружающей среды.

Вычислим работу, совершаемую идеальным газом при изотермическом изменении его объема от V₁ до V₂. Работа, производимая любой системой при изменении ее объема, как мы видели, определяется интегралом

(112)

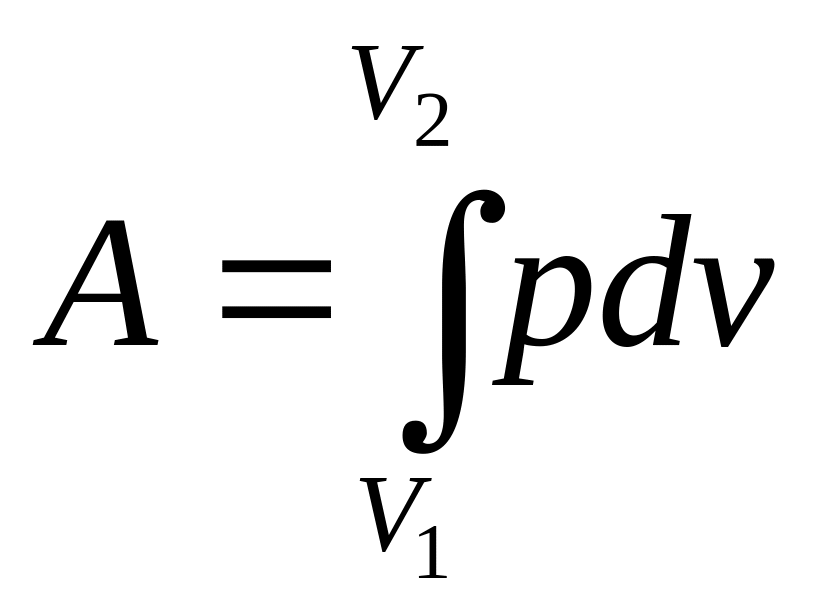
Чтобы произвести интегрирование, нужно знать, как при рассматриваемом процессе давление p связано с объемом V, т.е. необходимо знать уравнение процесса в переменных p, V. Уравнение изотермического процесса для идеального газа получается непосредственно из его уравнения состояния

(113)

Так как при изотермическом процессе T=const, то для данной массы газа и, следовательно,

(114)

где p₁ и V₁ ― значения давления и объема газа в начальном состоянии. Таким образом, при изотермическом процессе давление и объем идеального газа связаны между собой законом Бойля-Мариотта. Выражая из (114) давление газа через объем и значение параметров в начальном состоянии

(115)

и подставляя полученное выражение в (112), находим

(116)

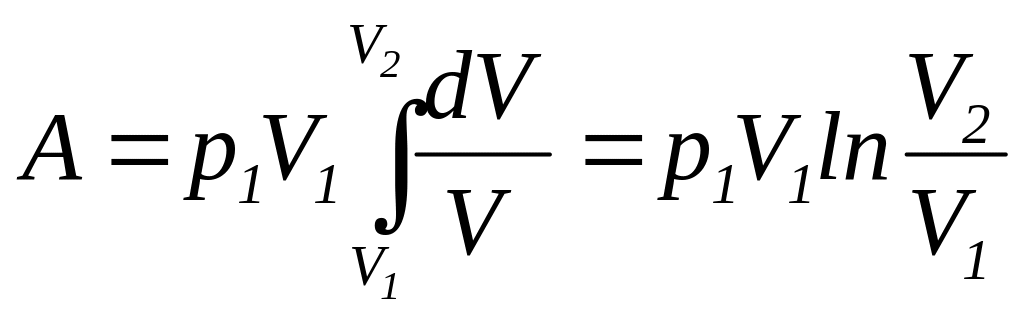
Так как , то формулу для работы идеального газа при изотермическом изменении его объема можно представить в виде

(117)

Из (116) и (117) видно, что работа идеального газа при изотермическом процессе изменения объема зависит не от разности объемов как для изобарического процесса, между которыми происходит расширение или сжатие, а от их отношения (т. е. степени расширения или сжатия газа).

Так как при изотермическом процессе работа A производится идеальным газом за счет передаваемого ему извне тепла, то полученные выше формулы могут в равной мере служить как для определения совершаемой газом изотермической работы, так и для расчета количества теплоты Q, необходимой для его изотермического расширения или сжатия

(118)