
- •Раздел II. Молекулярная физика
- •Глава1. Некоторые понятия молекулярной физики
- •§1 Массы атомов и молекул. Молярная масса
- •§2. Молекулярные силы
- •§3. Агрегатные состояния вещества. Особенности теплового движения в различных агрегатных состояниях вещества
- •§4. Равновесные процессы
- •Глава 2. Оcновы статической теории идеального газа
- •§1. Модель идеального газа
- •§2. Основное уравнение кинетической теории газов для давления
- •§3. Температура и её измерение. Опытные температурные шкалы.
- •2. Измерение давления газа при постоянном объёме производится с большей точностью, чем измерение объёма при постоянном давлении.
- •§4. Температура ― мера средней кинетической энергии поступательного движения молекул.
- •§5 Уравнение Менделеева-Клапейрона. Следствие из этого уравнения.
- •§6. Распределение Максвелла.
- •§7. Свойства распределения Максвелла.
- •§8. Распределение Больцмана. Барометрическая формула.
- •§ 9. Число степеней свободы молекул. Теорема о равномерном распределении энергии теплового движения по степеням свободы.
- •Глава 3. Основы термодинамики
- •§1. Внутренняя энергия, работа, теплота
- •§2. Первое начало термодинамики
- •§3. Теплоёмкость. Вычисление теплоёмкости идеального газа
- •§4. Изотермический процесс. Работа идеального газа при изотермическом изменении его объема
- •§5. Адиабатический процесс. Уравнение адиабаты идеального газа. Работа идеального газа при адиабатическом изменении его объема.
- •§6. Круговые обратимые процессы (циклы). Работа при круговом процессе. Первое начало термодинамики в применении к круговому процессу. Тепловые и холодильные машины
- •§7. Недостаточность первого начала термодинамики для однозначного описания процессов, происходящих в природе.
- •§8. Второе начало термодинамики. Формулировка основного постулата, выражающего второе начало термодинамики. Постулаты Кельвина и Клаузиуса и их эквивалентность
- •§9 . Цикл Карно и его кпд
- •§10. Математическое выражение второго начала термодинамики для обратимых процессов. Равенство Клаузиуса. Энтропия. Постоянство энтропии при обратимых процессах в замкнутой системе
- •§11. Основное уравнение термодинамики для обратимых процессов. Вычисление энтропии идеального газа.
- •§12. Второе начало термодинамики для необратимых процессов. Неравенство Клаузиуса. Возрастание энтропии при необратимых процессах в замкнутой системе. Общая формулировка второго начала термодинамики
- •§13. Примеры. Вычисление изменения энтропии при необратимых процессах
- •§14. Закон возрастания энтропии и превращение теплоты в работу
- •Глава 4. Реальные газы
- •§1. Экспериментальные изотермы. Область двухфазных состояний. Критическое состояние вещества
- •§2. Фазовая диаграмма жидкость-газ или кривая равновесия фаз
- •§З. Уравнение Ван-дер-Ваальса
- •§4. Изотермы Ван-дер-Ваальса и их сравнение с экспериментальными изотермами. Пересыщенный пар и перегретая жидкость
- •§5. Внутренняя энергия газа Ван-дер-Ваальса. Изотермическое расширение газа Ван-дер-Ваальса. Адиабатическое расширение газа Ван-дер-Ваальса в пустоту.
- •Глава 5. Столкновения молекул и явления переноса в газах
- •§1. Среднее число столкновений и средняя длина свободного пробега молекул
- •§2 Виды явлений переноса. Общее уравнение явлений переноса в газах
- •§3. Теплопроводность
- •§4. Вязкость
- •§5. Диффузия в газах
- •С точки зрения молекулярно кинетической теории за переносимую величину нужно взять концентрацию компоненты , рассчитанную на одну молекулу, т.Е.
- •Глава6. Твердые тела
- •§1. Аморфное и кристаллическое состояние вещества
- •§2. Классификация кристаллов по типу молекул, составляющих кристалл
- •§3. Анизотропия кристаллов
- •§4. Теплоемкость атомных кристаллов
- •Приложение а. Основные понятия теории вероятностей
- •§1. Понятие вероятности события
- •§2. Простейшие теоремы теории вероятностей
- •§3. Интегральная функция распределения случайной величины
- •§4. Плотность вероятности
- •§5. Среднее значение
§ 9. Число степеней свободы молекул. Теорема о равномерном распределении энергии теплового движения по степеням свободы.
Под числом степеней свободы механической системы понимают число независимых координат, определяющих положение системы в пространстве.
Одноатомную молекулу ( к примеру, He, Ar, Ne, Fe и т. д. ) можно рассматривать как материальную точку. Для задания её положения в пространстве достаточно задать три координаты ( x, y, z в декартовой или r, θ, φ в сферической системе координат). Таким образом, одноатомная молекула обладает тремя степенями свободы (i = 3).
Двухатомную молекулу представим как систему состоящую из двух материальных точек . Если расстояние l между атомами в молекуле не изменяется ( атомы в молекуле не колеблются ), то число степеней свободы равно пяти . В самом деле , если расстояние между атомами
(83) |
г
 де
де
![]() ― координаты i-го
атома в молекуле (i
=1,2) задано
, то всего имеется пять независимых
координат , шестая определяется из
условия (83). Положение двухатомной
молекулы, состоящей из двух жёстко
связанных атомов (точек) задают обычно
не пятью декартовыми координатами, а
тремя координатами центра С (рис. 7) масс
молекулы и двух углов θ
и φ,
определяющих направление в пространстве
прямой, проходящей через два атома
молекулы. Изменение координат центра
масс С(x,
y,
z)
при неизменных θ
и φ
характеризуется поступательным движением
молекулы. Поэтому у двухатомной молекулы
три (iпост
=3) поступательные
степени свободы. Изменение же углов θ
и φ
при неизменном положении центра масс
(точки С) характеризуется вращением
молекулы вокруг двух взаимно
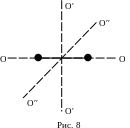
перпендикулярных осей O'O'
и O''O'',
перпендикулярных к оси ОО молекулы
(Рис. 8), в связи с этим у двухатомной
молекулы имеется две (iвр=2)
вращательные степени свободы. Если
расстояние между атомами в молекуле
меняется, то это означает, что атомы в
молекуле колеблются. В этом случае у
молекулы имеется шесть степеней свободы
(iпост=3,
iвр=2,
iкол=1).
― координаты i-го
атома в молекуле (i
=1,2) задано
, то всего имеется пять независимых
координат , шестая определяется из
условия (83). Положение двухатомной
молекулы, состоящей из двух жёстко
связанных атомов (точек) задают обычно
не пятью декартовыми координатами, а
тремя координатами центра С (рис. 7) масс
молекулы и двух углов θ
и φ,
определяющих направление в пространстве
прямой, проходящей через два атома
молекулы. Изменение координат центра
масс С(x,
y,
z)
при неизменных θ
и φ
характеризуется поступательным движением
молекулы. Поэтому у двухатомной молекулы
три (iпост
=3) поступательные
степени свободы. Изменение же углов θ
и φ
при неизменном положении центра масс
(точки С) характеризуется вращением
молекулы вокруг двух взаимно
перпендикулярных осей O'O'
и O''O'',
перпендикулярных к оси ОО молекулы
(Рис. 8), в связи с этим у двухатомной
молекулы имеется две (iвр=2)
вращательные степени свободы. Если
расстояние между атомами в молекуле
меняется, то это означает, что атомы в
молекуле колеблются. В этом случае у
молекулы имеется шесть степеней свободы
(iпост=3,
iвр=2,
iкол=1).
Т рехатомные
и многоатомные (с числом атомов
рехатомные
и многоатомные (с числом атомов
![]() )
по своему строению могут быть линейными
(например СО2)
или нелинейными (например молекулы
Н2О).
В первом случае (Рис. 9, а) равновесные
положения всех атомов расположения
всех атомов расположены вдоль одной
прямой. Если n-атомная
молекула (
)
имеет линейное строение, то в случае
жестких связей между атомами она обладает
пятью степенями свободы, как и двухатомная
(i=5,
iпост=3,
iвр=2).
Нелинейная же многоатомная молекула с
жесткой связью между атомами имеет, как
и твердое тело, шесть степеней свободы
(i=6,
iпост=3,
iвр=3).
При нежесткой связи между атомами
молекула обладает ещё дополнительными
степенями свободы колебательного
движения. При этом число колебательных
степей свободы возрастает с ростом
числа атомов в молекуле. Действительно,
если молекула состоит из n
атомов, не жестко связанных между собой,
то она имеет всего 3n
степеней, из которых 3 степени свободы
всегда относятся к поступательному
движению (iпост=3)
и три (iвр=3)
в случае нелинейной молекулы или две
(iвр=2)
в случае линейной молекулы к вращательному
движению. Остальные степени свободы
относятся к колебательному движению.
Таким образом, n-атомная
нелинейная молекула в общем случае
может иметь iкол=3n–6
колебательных степеней свободы, а
линейная ―
iкол=3n–5.
)
по своему строению могут быть линейными
(например СО2)
или нелинейными (например молекулы
Н2О).
В первом случае (Рис. 9, а) равновесные
положения всех атомов расположения
всех атомов расположены вдоль одной
прямой. Если n-атомная
молекула (
)
имеет линейное строение, то в случае
жестких связей между атомами она обладает
пятью степенями свободы, как и двухатомная
(i=5,
iпост=3,
iвр=2).
Нелинейная же многоатомная молекула с
жесткой связью между атомами имеет, как
и твердое тело, шесть степеней свободы
(i=6,
iпост=3,
iвр=3).
При нежесткой связи между атомами
молекула обладает ещё дополнительными
степенями свободы колебательного
движения. При этом число колебательных
степей свободы возрастает с ростом
числа атомов в молекуле. Действительно,
если молекула состоит из n
атомов, не жестко связанных между собой,
то она имеет всего 3n
степеней, из которых 3 степени свободы
всегда относятся к поступательному
движению (iпост=3)
и три (iвр=3)
в случае нелинейной молекулы или две
(iвр=2)
в случае линейной молекулы к вращательному
движению. Остальные степени свободы
относятся к колебательному движению.
Таким образом, n-атомная
нелинейная молекула в общем случае
может иметь iкол=3n–6
колебательных степеней свободы, а
линейная ―
iкол=3n–5.
Известно, что каждой степени свободы молекулы или любой другой механической системы соответствует определённой слагаемое в выражении для её кинетической энергии, так что общее число независимых слагаемых, на которые разлагается кинетическая энергия системы, всегда равно числу её степеней свободы. Так, например, кинетическая система одноатомной молекулы, имеющей 3 степени свободы, разлагается на три независимых слагаемых
(84) |
каждое из которых представляет собой кинетическую энергию соответствующую одной степени свободы.
Кинетическая энергия трех и многоатомной нелинейной молекулы с жесткой связью между атомами, имеющей 6 степеней свободы, содержит шесть независимых слагаемых
(85) |
Первые три слагаемых относятся к кинетической энергии поступательного движения центра масс молекулы, а следующие три ― к кинетической энергии вращательного движения вокруг трёх взаимно-перпендикулярных осей, проходящих через центр масс молекулы; wi ― угловые скорости вращения молекулы вокруг трёх указанных осей (i=1,2,3), Ii ―моменты инерции молекулы относительно этих осей.
При наличии колебательного движения атомов в молекуле в общее выражение для её кинетической энергии необходимо включить дополнительные слагаемые, соответствующие кинетической энергии колебательного движения.
Ответом на вопрос, какая энергия в среднем приходится на одну степень свободы, служит теорема Больцмана о равномерном распределении энергии теплового движения по степеням свободы: если система молекул или других частиц находится в тепловом равновесии при температуре Т, то средняя кинетическая энергия равномерно распределится между всеми степенями свободы и для каждой степени свободы она равна КТ/2.
Таким образом, если молекула имеет i степеней свободы, то её средняя кинетическая энергия будет равна
(86) |
т.е. средняя кинетическая энергия молекулы тем больше, чем сложнее молекула (чем больше степеней свободы).
Опыты по измерению теплоёмкостей показывают, что колебательные степени свободы в молекулах возбуждаются при достаточно больших температурах. Но при наличии у молекулы колебательных степеней свободы она будет обладать не только кинетической но и потенциальной энергией, причём для гармонических колебаний среднее значение кинетической и потенциальной энергии оказывается одинаковым. Поэтому на каждую колебательную степень приходится в среднем KT/2 энергии в виде кинетической и KT/2 в виде потенциальной, т.е. колебательная степень свободы обладает в два раза большей энергетической ёмкостью (KT/2+KT/2=KT) по сравнению с поступательной или вращательной. Ввиду этого при подсчёте числа степеней свободы i число колебательных степеней надо удваивать.
(87) |
