56.Принцип Даламбера для точки и механической системы.

Найдем сначала выражение принципа для одной материальной точки. Пусть на материальную точку с массой m действует система активных сил, равнодействующую которых обозначим , и реакция связи . Под действием этих сил точка будет двигаться по отношению к инерциальной системе отсчета с некоторым ускорением .

Введем величину (127) имеющую размерность силы. Векторную величину, = по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки.

Оказывается, что движение точки обладает следующим св-вом: если в любой момент времени к действующим на точку активным силам и реакции связи присоединить силу инерции, то полученная система сил будет уравновешенной, т. е. . (128)

Это положение выражает принцип Даламбера для материальной точки. Нетрудно убедиться, что оно эквивалентно второму закону Ньютона и наоборот. В самом деле, второй закон для рассматриваемой точки дает . Перенеся здесь величину в правую часть равенства и учитывая обозначение (127), придем к соотношению (128). Наоборот, перенося в уравнении (85) величину в другую часть равенства и учитывая обозначение (127), получим выражение второго закона Ньютона.

Рассмотрим теперь механическую систему, состоящую из n материальных точек. Выделим какую - нибудь из точек системы с массой m_k. Под действием приложенных к ней внешних и внутренних сил и (в которые входят и активные силы, и реакции связей) точка будет двигаться по отношению к инерциальной системе отсчета с некоторым ускорением . Введя для этой точки силу инерции , получим согласно равенству (128), что

(129)

т. е. что , и образуют уравновешенную систему сил. Повторяя такие рассуждения для каждой из точек системы, придем к следующему результату, выражающему принцип Даламбера для системы: если в любой момент времени к каждой из точек системы кроме действующих на нее внешних и внутренних сил присоединить соответствующие силы инерции, то полученная система сил будет уравновешенной и к ней можно применять все уравнения статики.

Математически принцип Даламбера для системы выражается n векторными равенствами вида (129), которые, очевидно, эквивалентны дифф-м ур-м движения системы (102). , из принципа Даламбера, как и из уравнений (102), можно получить все общие теоремы динамики.

И ИЗГИБАЮЩИХ МОМЕНТОВ. ЗАВИСИМОСТЬ МЕЖДУ ИЗГИБАЮЩИМ МОМЕНТОМ И КРИВИЗНОЙ ОСИ ИЗОГНУТОГО СТЕРЖНЯ ПРИ ЧИСТОМ ИЗГИБЕ. ЖЁСТКОСТЬ ПРИ ИЗГИБЕ.

Ч тобы построить эпюр изгибающего момента, необходимо мысленно разделить балку на участки, в каждом участке провести сечения и определить изгибающие моменты отдельно для каждого сечения. Сечения проводятся начиная с незакреплённого конца. Изгибающий момент находится как сумма моментов внешних сил. расположенных справа (слева) от сечения (с той стороны, с которой расположена оставшаяся часть балки). Момент берём со знаком плюс, если балка изгибается выпуклостью вниз, если вверх – минус. По получившемуся уравнению для изгибающего момента на данном участке, определяем фигуру, соответствующую эпюре этого участка. Определяя моменты на крайних точках участка, строим эпюру. Для построения эпюры поперечных сил, находим сумму проекций сил на вертикальную ось, расположенных по правую (левую) сторону от данного сечения. Поперечная сила положительна на тех участках, где эпюра изгибающего момента восходящая (при движении слева направо), и отрицательная на тех участках, где она нисходящая.

Рассмотрим на примере (см. рисунок).

Участок АВ: Mz1=-qz1(z1/2)= -q /2 – парабола

=0 M=0; z1=a1/2 M= -q /8; z2=a1 M= q /2

Qz1=-qz1; z1=0 Qz1=0; z1=a1 Qz1=qa1

Участок ВС: Mz2=-qa1(z2-a1/2) – прямая

z2=a1 M=-q /2; z2=a1+a2 M=-qa(a1/2+a2)

Qz2=qa1

1/ρ=M/(EI_x). Величина K=1/ρ представляет собой кривизну нейтрально­го слоя балки.

Кривизна оси балки при изгибе пропорциональна изги­бающему моменту и обратно пропорциональна величине ЕI_x, на­зываемой жесткостью балки.

.ПОНЯТИЕ ОБ УСТОЙЧИВЫХ И НЕУСТОЙЧИВЫХ ФОРМАХ РАВНОВЕСИЯ. КРИТИЧЕСКАЯ НАГРУЗКА.

Под устойчивостью мы интуитивно понимаем свойство системы сохранять свое состояние при внешних воздейст­виях. Если система таким свойством не обладает, она назы­вается неустойчивой. В равной мере можно сказать, что неустойчивым является ее состояние.

В реальных условиях всегда существует возможность пере­хода к новому состоянию в неустойчивой системе. В этом случае говорят, что произошла потеря устойчивости.

Система при потере устойчивости может вести себя по-разному. Обычно происходит переход к некоторому новому положению равновесия, что в подавляющем большинстве случаев сопровождается большими перемещениями, возникновением пластических деформаций или полным разрушением. В некоторых случаях при потере устойчивости конструкция продолжает работать и выполняет по-прежнему свои основные функции, как, например, тонкостенная обшивка в самолетных конструкциях. Возможны, наконец, и такие случаи, когда потерявшая устойчи­вость система, не обла­дая устойчивыми поло­жениями равновесия, переходит в режим не­затухающих колебаний,

При проектировании подобных конструкций одновременно с расчетом на прочность ведется и расчет на устойчивость как отдельных узлов, так и системы в целом.

Одной из мер повышения запаса устойчивости системы является увеличение ее жесткости. Предполагается, что система является идеальной, т.е. если речь идет о сжатом стержне, ось его строго прямолинейна, материал однороден, силы приложены центрально. Если рассматривается цилиндрическая оболочка, то также считается, что она имеет совершенную форму и нагрузка не отступает от предписанных законов распределения. Идеальной системе сообщается отклонение от положения равновесия. При этом рассматриваются отклонения, которые не только являются малыми, но могут быть сделаны меньше любой наперед заданной малой величины. Если после устранения причин, вызвавших отклонение система возвращается к исходному состоянию равновесия, то послед­нее считается устойчивым. Если не возвращается, то поло­жение равновесия считается неустойчивым. Силы инерции, возникающие при движении системы, не учитываются.

Такая расчетная схема дает возможность поставить яв­ление потери устойчивости на расчетную основу и опреде­лять условия перехода от устойчивого состояния к неустойчивому. Параметры, характеризующие такой переход, на­зываются критическими. В частности, обобщенная сила, превышение которой приводит к переходу от устойчивого равновесия к неустойчивому, называется критической си­лой.

При расчете на устойчивость рабочая нагрузка назначается как п-я доля критической. Под п понимается коэффрициент запаса устойчивости, значение которого, как и при расчетах па прочность, назначается в зависимости от кон­кретных обстоятельств, связанных со спецификой техноло­гии, с условиями эксплуатации, а также со степенью ответственности конструкции.

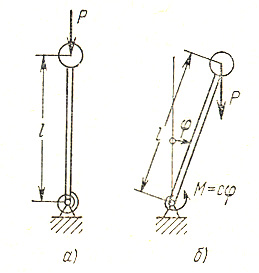
Определение критических нагрузок

На конце жесткого стержня (перевернутого маятника, показанного на рис. укреплен груз Р. Внизу стержень имеет шарнир и удерживается в вертикальном положении упругой пружиной, имеющей линейную характеристику. Это значит, что при повороте стержня на угол φ в шарнире возникает момент, равный сφ, где с — жесткость пружины.

Эта модель, обладая предельной простотой, сохраняет в себе все основные свойства характер­ные для более сложных задач.

Приравнивая момент силы Р шарнирному моменту, по­лучим Plsinφ=cφ. Так как угол φ мал, то sinφ≈φ; тогда (Pl–c)φ=0 и мы получаем два возможных решения.

Первое из них, φ=0, означает, что при вертикальном по­ложении маятника условие равновесия выполняется при любом значении силы Р, что совершенно очевидно. Такое решение называют обычно тривиальным.

Имеется вторая возможность. Пусть φ≠0, и маятник, следовательно, отклонен от вертикали. Тогда условие равно­весия выполняется при Р=с/l, и вблизи исходного состояния равновесия обнаруживается второе состояние равновесия, сколь угодно близкое к первому. Силу, соответствующую этой, как говорят, бифуркации форм равновесия, мы при­нимаем за критическую.