52.Механическая система. Силы внешние и внутренние. Масса системы. Центр масс. Дифференциальные уравнения движения системы. Теорема о движении центра масс. Закон сохранения движения центра масс.

- Механическая система. Силы внешние и внутренние

Систему материальных точек или тел, движение (или равновесие) которой рассматривается, называют механической системой. Если между точками (телами) механической системы действуют силы взаимодействия, то она обладает том свойством, что в ней положение или движение каждой точки (тела) зависит от положения и движения всех остальных. Классическим примером такой системы является солнечная система, в которой все тела связаны силами взаимного притяжения.

Действующие на механическую систему активные силы и реакции связей разделяют на внешние и внутренние . Внешними называют силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы. Внутренними называют силы, с которыми точки или тела данной системы действуют друг на друга. Это разделение является условным и зависит от того, какая механическая система рассматривается.

Внутренние силы обладают следующими свойствами:

I. Геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю. В самом деле, по 3-му закону динамики любые две точки системы (рис. 37) действуют друг на друга с равными по модулю и противоположно направленными силами и , сумма которых равна нулю: .

II. Сумма моментов (главный момент) всех внутренних сил системы относительно любого центра или оси равняется нулю. Действительно, если взять произвольный центр О, то из рис.37 видно, что . Аналогичный результат получится при вычислении моментов относительно оси. , и для всей системы будет: и .

- Масса системы. Центр масс

Движение системы кроме действующих сил зависит также от ее суммарной массы и распределения масс. Масса системы (обозначаем М или т) равна арифметической сумме масс всех точек или тел, образующих систему:

Р аспределение масс в системе определяется значениями масс m_k ее точек и их взаимными положениями, т. е. их координатами х_k, у_k, z_k . Однако оказывается, что при решении тех задач динамики, которые мы будем рассматривать, в частности динамики твердого тела, для учета распределения масс достаточно знать не все величины m_k, х_k, у_k, z_k , а некоторые, выражаемые через них суммарные характеристики. Ими являются: координаты центра масс (выражаются через суммы произведений масс точек системы на их координаты), осевые моменты инерции (выражаются через суммы произведений масс точек системы на квадраты их координат) и центробежные моменты инерции (выражаются через суммы произведений масс точек системы и двух из их координат).

Центр масс. В однородном поле тяжести, для которого g=const, вес любой частицы тела пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Преобразуем формулы (29), определяющие координаты центра тяжести тела, к виду, явно содержащему массу. Для этого положим в названных формулах р_k=m_kg и Р=mg, после чего, сократив на g, найдем:

, , (100)

В полученные равенства входят теперь массы т_k материальных точек (частиц), образующих тело, и координаты х_k, y_k, z_k, этих точек. Следовательно, положение точки С(x_C, у_C, z_C) действительно характеризует распределение масс в теле или в любой механической системе, если под m_k, х_k, у_k, z_k понимать соответственно массы и координаты точек системы.

Геометрическая точка С, координаты которой определяются формулами (100), называется центром масс или центром инерции механической системы.

Если положение центра масс определять его радиусом-вектором , то из равенств (100) для получается формула (101), где – радиус -векторы точек, образующих систему.

Из полученных результатов следует, что для твердого тела, находящегося в однородном поле тяжести, положения центра масс и центра тяжести совпадают. Но в отличие от центра тяжести понятие о центре масс сохраняет свой смысл для тела, находящегося в любом силовом поле (например, в центральном поле тяготения).

-Дифференциальные ур-я движения системы

Рассмотрим систему, состоящую из п материальных точек. Вы­делим какую-нибудь точку системы с массой m_k. Обозначим равнодействующую В1-сх приложенных к точке внешних сил (и активных, и реакций связей) через , а равнодействующую всех внутренних сил – через , Если точка имеет при этом ускорение , то по основному закону динамики .

Аналогичный результат получим для любой точки. , для всей системы:

(102)

Ур-я (102) представляют собой дифф. ур-я движения системы в векторной форме. Входя­щие в правые части ур-я силы могут в общем случае зависеть от времени, координат точек системы и их скоростей.

Проектируя равенства (102) на какие-нибудь координатные оси, получим дифф-е ур-я движения системы в проекциях на эти оси.

Полное решение основной задачи динамики для системы будет состоять в том, чтобы, зная заданные силы и наложенные связи, проинтегрировать соответствующие дифф-е ур-я и определить в резулътате закон движения каждой из точек системы и реакции связей.

- Теорема о движении центра масс

В ряде случаев для определения характера движения системы (особенно твердого тела) требуется знать закон движения ее центра масс. Чтобы найти этот закон, обратимся к ур-ям движения системы (102) и сложим почленно их левые и правые части. Получим (103)

Преобразуем левую часть равенства. Из формулы (101) для радиуса-вектора центра масс имеем .

Беря от обеих частей этого равенства вторую производную по времени и замечая, что производная от суммы равна сумме производ­ных, найдем

или (104)

где – ускорение центра масс системы. По свойству внутренних сил системы , получим окончательно из равенства (103), учтя (104): . (105)

Уравнение (105) и выражает теорему о движении центра масс системы: произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил. Сравнивая уравнение (105) с уравнением движения материальной точки придем к другому выражению теоремы: центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему.

П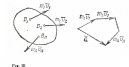 роектируя обе части равенства (105) на координатные оси, по­лучим:

, , . (106)

Эти уравнения представляют собой дифференциальные уравнения движения центра масс в проекциях на оси декартовой системы координат.

-Закон сохранения движения центра масс

Из теоремы о движении центра масс можно получить следующие важные следствия.

1. Пусть сумма внешних сил, действующих на систему, равна нулю: .

Тогда из уравнения (105) следует, что или =соnst.

, если , то центр масс этой системы движется с постоянной по модулю и направлению скоростью, т.е. равномерно и прямолинейно. В частности, если вначале центр масс был в покое, то он и останется в покое. Действие внутренних сил, как мы видим, движение центра масс системы изменить не может.

2. Пусть сумма внешних сил, действующих на систему, не равна нулю, но эти силы таковы, что сумма их проекций на какую-нибудь ось (например, ось х) равна пулю: .

Тогда первое из уравнений (106) дает или .

, если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция скорости центра масс системы на эту ось есть величина постоянная. В частности, если в начальный момент , то и в любой последующий момент времени , т.е. центр масс системы в этом случае вдоль оси х перемещаться не будет (x_C=const).

Все эти результаты выражают собой закон сохранения движения центра масс системы.