Тема 5. Динамический анализ машин и механизмов

Динамика – раздел механики машин и механизмов, изучающий закономерности движения звеньев механизма под действием приложенных к ним сил. Существует определение, по которому «динамика рассматривает силы в качестве причины движения тел».

В основе динамики лежат три закона, сформулированные Ньютоном, из которых следует:

1. Если равнодействующая всех внешних сил, действующих на механическую систему равно нулю, то система находится в состоянии покоя (из первого закона).

2. Изменение состояния движения механической системы может быть вызвано либо изменением действующих на нее внешних сил, либо изменением ее массы (из второго закона).

Из этих же законов следует, что динамическими параметрами механической системы являются:

• инерциальные (массы (m) и моменты инерции (I));

• силовые (силы (F_ij) и моменты сил (M_ij));

• кинематические (линейные (a) и угловые () ускорения).

В общей постановке динамика – изучение каких-либо процессов или явлений в функции времени.

Динамическая модель – модель системы, предназначенная для исследования ее свойств в функции времени (или модель системы, предназначенная для исследования в ней динамических явлений).

Прямая задача динамики – определение закона движения системы при заданном управляющем силовом воздействии.

Обратная задача динамики – определение требуемого управляющего силового воздействия, обеспечивающего заданный закон движения системы.

Методы составления уравнений (динамической модели системы):

• энергетический (уравнения энергетического равновесия – закон сохранения энергия);

• кинетостатический (уравнения силового равновесия с учетом сил инерции по принципу Даламбера).

Прямая задача динамики машин. Прямой задачей динамики машины является анализ, определение закона движения механической системы под действием заданных внешних сил. При решении этой задачи параметры машинного агрегата и действующие на него внешние силы известны, необходимо определить закон движения: скорости и ускорения в функции времени или обобщенной координаты. Иначе эту задачу можно сформулировать так: заданы управляющие силы и силы внешнего сопротивления, необходимо определить обеспечиваемый ими закон движения машины. Обратная задача динамики машины – это задача синтеза управления, когда задан требуемый закон движения машины и внешние силы сопротивления, а определяются управляющие силы.

При решении задач динамики используются либо уравнения силового равновесия системы – метод кинетостатики, либо уравнения энергетического равновесия – закон сохранения энергии. Для идеальной механической системы, в которой нет потерь энергии и звенья абсолютно жесткие, этот закон можно применять в виде теоремы о изменении кинетической энергии. Согласно этой теореме, работа всех внешних сил, действующих на систему, расходуется только на изменение ее кинетической энергии. При этом потенциальные силы – силы веса – рассматриваются, как внешние:

,

где T – изменение кинетической энергии системы;

T – текущее значение кинетической энергии системы;

T_нач – начальное значение кинетической энергии системы;

– суммарная работа внешних сил, действующих на систему.

Рассмотрим сложную механическую систему (рис. 3.3.19), состоящую из n подвижных звеньев, из которых r – звеньев совершают вращательное движение, j – плоское, k – поступательное. Основная подвижность системы (W) равна 1. На систему действуют внешние силы (f) и внешние моменты (m). Движение этой системы определяется изменением одной независимой обобщенной координаты. Такую систему при решении задач динамики можно заменить более простой динамической моделью. Положение звена этой модели определяется обобщенной координатой, а динамические параметры заменяются: инерционные – суммарным приведенным моментом инерции (I^пр), силовые – суммарным приведенным моментом (М^пр). Эти параметры динамической модели рассчитываются по критериям подобия модели и объекта, которые определяются соответственно из равенства правых и левых частей уравнений изменения кинетической энергии для модели и объекта, т.е.

, ,

где – сумма работ всех внешних сил, действующих на систему;

– работа суммарного приведенного момента;

– сумма кинетических энергий звеньев системы;

– кинетическая энергия динамической модели.

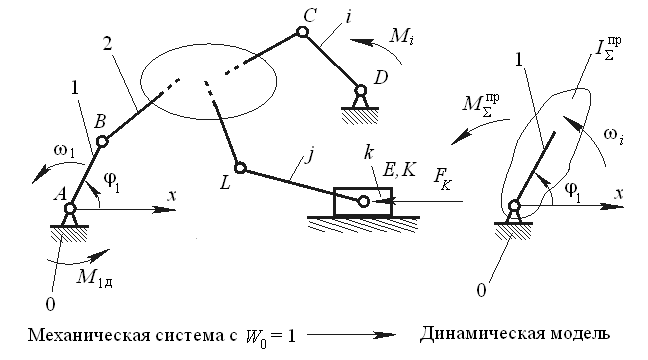
Рис. 3.3.19

Понятия звена приведения и приведенных величин. Использование приведенных величин основывается на известном из кинематического анализа механизмов положении: если кинематическая цепь является механизмом, то по законам движения входных звеньев можно определить законы движения остальных его звеньев. Поэтому вместо исследования движения всех звеньев кинематической цепи механизма записывают уравнение только для звеньев приведения. Под звеном приведения понимают звено, обычно совершающее поступательное или вращательное движение. На него действуют условные силовые факторы, совершающие механическую работу, равную работе всех сил и моментов сил, действующих на звенья механизма, и оно обладает кинетической энергией, равной кинетической энергии всех звеньев механизма.

Из понятия звена приведения вытекают следующие понятия.

Приведенная сила (F_п) (момент приведенной силы (М_п)) – условная сила (момент), которая, будучи приложена в какой-либо точке звена приведения, при заданном положении входного звена совершает в единицу времени механическую работу, численно равную сумме работ всех сил и моментов сил, действующих на звенья механизма. Так как речь идет об условных силовых факторах, то обычно выбирают точку приложения приведенной силы, скорость которой известна, и направление ее вектора принимают совпадающим с направлением вектора скорости.

Из определения приведенной силы (момента) вытекают зависимости для нахождения их величин, в которых учтено, что механическая работа в единицу времени равна мощности:

; (3.3.32)

. (3.3.33)

Приведенная масса (m_п) (приведенный момент инерции (I_п)) механизма – условная масса (момент инерции), которая, будучи сосредоточена в какой-либо точке звена приведения, обладает кинетической энергией, численно равной кинетической энергии всех звеньев механизма при заданном положении входного звена.

Из этого определения следует, что величины приведенной массы и приведенного момента инерции определяются из зависимостей

; (3.3.34)

. (3.3.35)

где S_i – центр масс звена i.

Анализ выражений (3.3.32) – (3.3.35) показывает, что значе­ния приведенной силы и ее момента, приведенной массы и приведенного момента инерции зависят только от отношения скоростей звеньев и их точек к скорости звена приведения или какой-либо его точки.

Из изучения кинематики механизмов известно, что отношения скоростей звеньев и точек определяются передаточной функцией и не зависят от абсолютных значений кинематических факторов. Поэтому в динамических расчетах шарнирных механизмов отношения скоростей для реализации зависимостей (3.3.32) – (3.3.35) определяют для единичных значений скоростей входных звеньев механизмов, а в зубчатых механизмах – через величины передаточных отношений.

Определение параметров динамической модели машины (приведение сил и масс). Рассмотрим изображенную на рис. 3.3.19 механическую систему и ее динамическую модель. Запишем для них уравнения изменения кинетической энергии.

Кинетическая энергия:

• для механической системы: ;

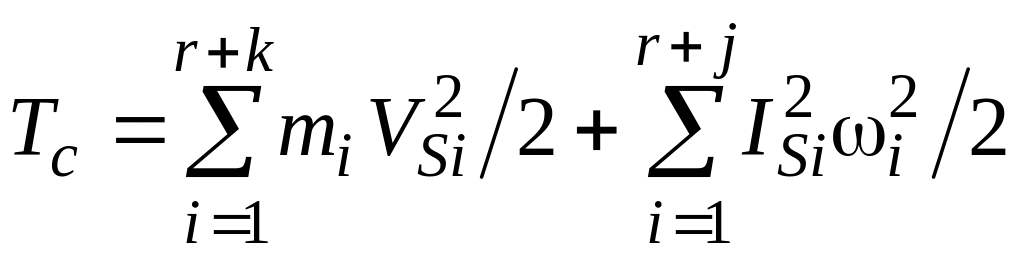• для модели: .

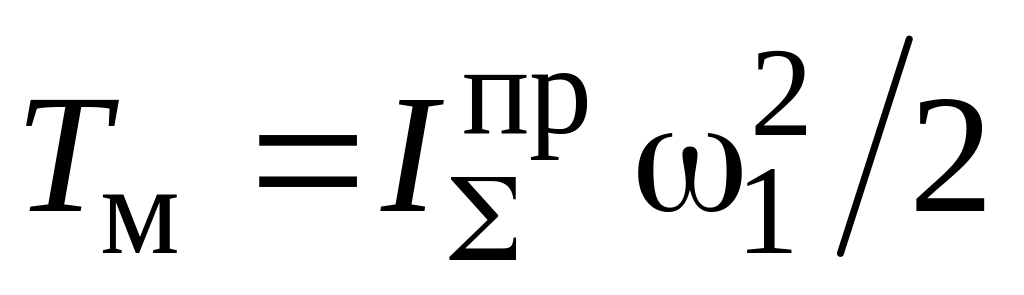Суммарная работа внешних сил:

• для механической системы:

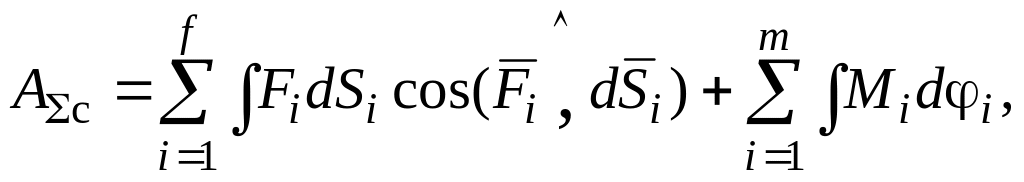
• для модели:

.

Модель будет энергетически эквивалентна рассматриваемой механической системе, если правые и левые части уравнений изменения кинетической энергии для модели и для системы будут соответственно равны. То есть для левых частей выполняется условие Т_с = Т_м, а для правых – . Для того чтобы второе равенство выполнялось в течение всего диапазона изменения обобщенной координаты, необходимо обеспечить не равенство интегралов, а равенство подынтегральных выражений: . Подставляя в равенства, записанные ранее выражения для кинетических энергий и работ получим:

• для левых частей:

;

• для правых частей:

.

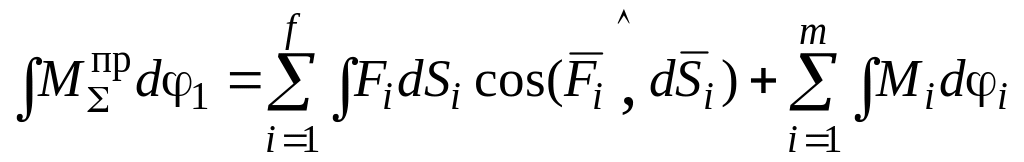Из уравнения для левых частей получаем формулу для определения приведенного суммарного момента инерции динамической модели:

.

Из уравнения для правых частей получаем формулу для определения приведенного суммарного момента динамической модели:

.

Уравнения движения динамической модели.

1. Уравнение движения динамической модели в интегральной форме.

Запишем для динамической модели теорему об изменении кинетической энергии:

,

где

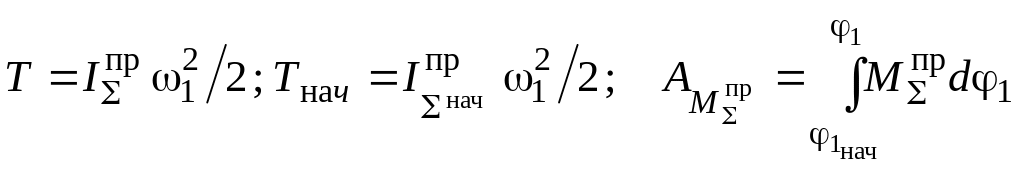
Ууравнение движения динамической модели в интегральной или энергетической форме имеет вид:

.

Из этого уравнения после преобразований получим формулу для расчета угловой скорости звена приведения

.

Для машин, работающих в режиме пуск-останов ( и ) формула принимает вид

.

2. Уравнение движения динамической модели в дифференциальной форме.

Продифференцируем полученное выше уравнение по обобщенной координате:

,

где

.

После подстановки получим уравнение движения динамической модели в дифференциальной форме

.

Из этого уравнения после преобразований получим формулу для расчета углового ускорения звена приведения

Для механических систем, в которых приведенный момент не зависит от положения звеньев механизма,