Тема 7. Сложное сопротивление. Расчет по теориям прочности

Косой изгиб. Большинство ответственных деталей и узлов авиационной техники работают в условиях сложного сопротивления. Так, например, крыло самолета в целом, его лонжероны и другие элементы подвергаются одновременно изгибу и кручению. Эти же деформации испытывают фюзеляж самолета и валы передач двигателя. Узел крепления двигателя к фюзеляжу – рама, а также стойка шасси самолета работают на изгиб и растяжение – сжатие.

До сих пор мы рассматривали плоский изгиб, когда плоскость дейс­твия нагрузок совпадала с продольной плоскостью симметрии балки или вообще с одной из ее главных плоскостей. Деформация изгиба при этом происходила в плоскости действия моментов, а нейтральная ось совпадала с главной осью инерции поперечного сечения и была перпендикулярна к плоскости действия моментов. Однако бывают случаи, когда плоскость действия изгибающих моментов не совпадает ни с одной из главных плоскостей балки. Такой изгиб называется косым изгибом.

Рассмотрим пример косого изгиба. Пусть балка прямоугольного сечения, защемленная одним концом (рис. 3.2.35, а, б) изгибается силой F, действующей перпендикулярно к оси балки на свободном конце и составляющей угол с главной плоскостью ху.

Так как плоскость действия изгибающего момента в данном случае не совпадает ни с одной из главных плоскостей балки, то это будет случай косого изгиба. Абсолютное значение изгибающего момента в каком-либо сечении, отстоящем на расстоянии х от защемления, будет равна

М = F(l – х).

Разложим силу F на две составляющие F_z и F_y, действующие по главным осям сечения у и z. Тогда абсолютные значения составляющих моментов будут равны;

М_z = F_y(l – x) = F(l – x)cos,M_y = F_z (l – x) = F(l – x)sin.

Моменты M_y и М_z действуют в главных плоскостях балки. Напряжения от каждого из этих моментов, взятых в отдельности, мы определять умеем. Пользуясь законом независимости действия сил, можно найти напряжения, получающиеся при одновременном действии моментов M_y и М_z.Таким образом, случай косого изгиба можно всегда свести к двум плоским, или, как иногда говорят, к простым изгибам.

При действии только одного момента М_z нейтральной осью будет ось z (рис. 3.2.35, в), и нормальное напряжение для какой-либо точки N с координатами z, у, взятой в первом квадранте сечения mn, определяется по формуле

₁ = .

Напряжение в той же точке от действия только момента М_y (рис. 3.2.35, г) равно:

₂ = .

Рис. 3.2.35

При одновременном действии двух моментов М_y и M_z напряжение в любой точке сечения будет равно алгебраической сумме напряжений ₁ и ₂ т.е.

 = ₁ + ₂= . (3.2.28)

В эту формулу координаты у, z точек сечения и изгибающие моменты подставляются со своими знаками. Координаты z и у положительны в первой четверти, отрицательны в третьей четверти, во второй четверти у положительна z отрицательна, а в четвертой четверти у отрицательна, z положительна. Если момент действует так, что в рассматриваемой четверти он вызывает растяжение, то ему приписывается знак плюс, а если сжатие, то минус. Наибольшее суммарное напряжение будет в точках В и С. Абсолютные значения этих напряжений будут одинаковы. Уравнение нейтральной линии получим, приравнивая нулю правую часть формулы (3.2.28):

= 0 или .

Этому уравнению прямой линии удовлетворяют значения у = 0 и z = 0; сле-довательно, нейтральная линия проходит через центр тяжести поперечного сечения. Определив из последнего выражения отношение у/z, найдем тангенс угла, составляемого нейтральной линией с положительным направлением оси z (рис. 3.2.35, д):

tg= = – tg .

Из формулы видно, что для таких сечений, у которых J_y = J_z (квадрат, круг и др.), нейтральная линия всегда будет перпендикулярна к плоскости действия изгибающего момента, в которой и будет происходить деформация изгиба, не может быть косого изгиба.

Гипотезы прочности. Выше рассматривалась работа материалов при различных видах деформаций, существующих раздельно и при которых возникают напряжения или только нормальные или касательные. Напряжения при таких видах деформаций в каждой точке сечения можно складывать алгебраически.

Часто встречаются и имеют большое практическое значение случаи сочетания основных видов деформаций, когда в поперечных сечениях возникают и нормальные, и касательные напряжения, распределенные неравномерно и по разным законам. Для таких случаев опытное определение величин, характеризующих прочность, невозможно.

При оценке прочности приходится основываться на механических характеристиках материала, полученных из диаграммы растяжения, а условия прочности составляются на основе научных предположений (гипотез) о том, какой фактор вызывает появление опасного состояния. Можно полагать, что опасное состояние возникает при достижении нормальными напряжениями предела текучести или предела пропорциональности. С другой стороны, можно полагать, что опасное состояние возникает тогда, когда наибольшее относительное удлинение достигает определенного значения.

Возможно и третье предположение, что появление опасного состояния связано с тем, что касательные напряжения достигают определенного значения. Возникновение опасного состояния можно связать также с достижением определенного значения величины энергии, накапливаемой в материале при деформации.

На основе указанных выше возможных критериев опасного состояния разработано пять теорий прочности. Подробное рассмотрение этих теорий выходит за пределы нашей учебной программы. Для расчета валов, болтовых соединений, винтов домкратов и др. применяют третью или пятую теорию прочности.

Изгиб с кручением. Случаем совместного действия изгиба и кручения является передача мощности валом. Для расчета валов на совместное действие изгиба и кручения применяют третью или пятую теорию прочности.

По третьей теории прочности (теория наибольших касательных напряжений), эквивалентное напряжение вычисляют по формуле

_экв = . (3.2.29)

По пятой теории прочности (энергетическая теория), формула для эквивалентных напряжений имеет вид

_экв = .^. (3.2.30)

В этих формулах и нормальное и касательное напряжения в опасной точке поперечного сечения бруса.

Максимальные нормальные и касательные напряжения у круглых валов вычисляют по формулам:

; ,

где полярный момент сопротивления (W_), и осевой момент (W_х) связаны равенством

W_ = 2W_х.

При сочетании изгиба и кручения опасными будут точки поперечного сечения вала, наиболее удаленные от нейтральной оси.

Подставим значения напряжений в принятые уравнения теорий прочности, получим

_экв = и _экв = .

Выражение, стоящее в числителе, назовем эквивалентным моментом.

Расчетная формула для круглых валов принимает вид

_экв = . (3.2.31)

Кручение и растяжение или сжатие. Сочетание деформаций кручения и растяжения испытывают, например, болты и крепежные винты, а сочетание кручения и сжатия – винты домкратов и т.д. Нормальные и максимальные касательные напряжения в этих случаях вычисляют по формулам

 = ;  = .

Применив третью теорию прочности, получим расчетную формулу

_экв = . (3.2.32)

Применив пятую теорию прочности, получим

_экв = . (3.2.33)

Внецентренное растяжение – сжатие. Рассмотрим нагружение бруса осевой силой F, параллельной оси, приложенной в некоторой точке Е, т.е. действующей с некоторым эксцентриситетом е. В этом случае брус испытывает внецентренное растяжение. Приложим в точке О две равные и противоположно направленные силы F и F, равные F, от этого ни равновесие бруса, ни напряжения в его поперечных сечениях не изменятся.

Рассматривая отдельно эти силы, можно сделать вывод, что сила F вызывает растяжение, а оставшаяся пара сил образует момент Fе, изгибающий брус.

Сила F, действующая по оси бруса, вызывает напряжение растяжения, которое определяется по формуле

,

это напряжение распределяется равномерно по всему поперечному сечению бруса и имеет одинаковую величину в любом сечении (рис. 3.2.36, б).

И згибающий момент Fe постоянен по длине бруса. Он вызывает чистый изгиб, при котором возникают напряжения

.

Из рис. 3.2.36 видно, что верхние волокна бруса растягиваются силой F и изгибающим моментом Fе, а нижние волокна растягиваются силой F и сжимаются изгибающим моментом Fе. При этом в одной и той же плоскости возникают нормальные напряжения и, следовательно, суммарные напряжения будут равны алгебраической сумме напряжений (_р + _и), тогда

.

Таким образом, в верхних волокнах возникают максимальные напряжения, в нижних – минимальные:

; .

Расчет тонкостенных осесимметричных оболочек. Тонкостенной осесимметричной называется оболочка, имеющая форму тела вращения, толщина которой весьма мала по сравнению с радиусами кривизны ее поверхности.

Н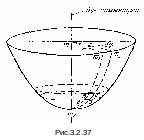 а рис. 3.2.37 изображена серединная (серединной называется поверхность, равноудаленная от наpужной и внутренней поверхностей оболочки) поверхность осесимметричной оболочки. Выделим из нее бесконечно малый элемент двумя меридиональными плоскостями mm₁m₂ и тт₃т₂ (т. е. плоскостями, проходящими через ось симметрии оболочки) с углом d между ними и двумя плоскостями, перпендикулярными оси симметрии оболочки, одна из которых пересекает срединную поверхность оболочки по линии ВС, а другая по линии AD.

Радиусы кривизны срединной поверхности элемента ABCD в меридиональной плоскости обозначим _m, а радиусы ее кривизны в плоскости, перпендикулярной меридиану, – _ (рис. 3.2.38).

Расчеты тонкостенных осесимметричных оболочек выполняют при проектировании различных резервуаров, газгольдеров, котлов и т. д. Нагрузки, действующие на внутреннюю поверхность такой оболочки, перпендикулярны этой поверхности и симметричны относительно оси симметрии оболочки.

Рис. 3.2.38

Если оболочка достаточно тонкая, при расчете можно пренебречь изгибом поверхности оболочки и считать, что напряжения по толщине стенки оболочки распределены равномерно. Такой расчет называется расчетом по безмоментной теории. Если оболочка недостаточно тонкая, имеет резкие переломы в очертании, жесткие закрепления и нагружена сосредоточенными силами или моментами, то в зонах, прилегающих к местам переломов, закреплений, приложения нагрузки, а также у краев оболочки возникает изгиб. Однако по мере удаления от этих мест изгибающие моменты быстро затухают; поэтому расчет удаленных зон таких оболочек может производиться по безмоментной теории.

Элемент ABCD оболочки в ортогональных проекциях показан на рис. 3.2.38, а. По боковым граням элемента АВ и CD, совпадающим с меридиональными плоскостями, в силу симметрии оболочки и нагрузки касательные напряжения равны нулю; по этим граням действуют лишь нормальные напряжения _ (окружные напряжения).

Из закона парности касательных напряжений следует, что касательные напряжения по боковым граням ВС и AD также равны нулю; по этим граням действуют лишь нормальные напряжения _m (меридиональные напряжения). Кроме напряжений _ и _m на элемент оболочки действует нагрузка в виде давления р, перпендикулярного поверхности ABCD.

Из условия равновесия бесконечно малого элемента оболочки в виде суммы проекций приложенных к нему сил на ось v, совпадающую с нормалью к поверхности ABCD можно вывести уравнения Лапласа:

, (3.2.34)

где  – толщина элемента ABCD оболочки.

Формула (3.2.34) используется для определения напряжений в стенке тонкостенной оболочки.

Из одного уравнения (2.2.34) две неизвестные величины _ и _m определить невозможно; поэтому напряжения в стенке оболочки можно найти лишь на основе совместного решения уравнения Лапласа и уравнения равновесия части оболочки, отсеченной конической поверхностью, перпендикулярной меридианам. Исключением является сферическая (шаровая) оболочка, находящаяся под действием газового давления; для нее

,

где D – диаметр сферы.

Вследствие центральной симметрии оболочки и действующей на нее нагрузки _ = _m, а потому из уравнения (3.2.34)

. (3.2.35)

Для оболочки, имеющей форму цилиндра или конуса, из уравнения Лапласа можно определить _, даже если _m еще неизвестно. Это следует из того, что в указанных случаях _m =  (меридиан оболочки представляет собой прямую линию) и, значит, _m/_m = 0, поэтому

.